Multifrequency Induced-Charge Electroosmosis
Abstract
:1. Introduction
2. Methods
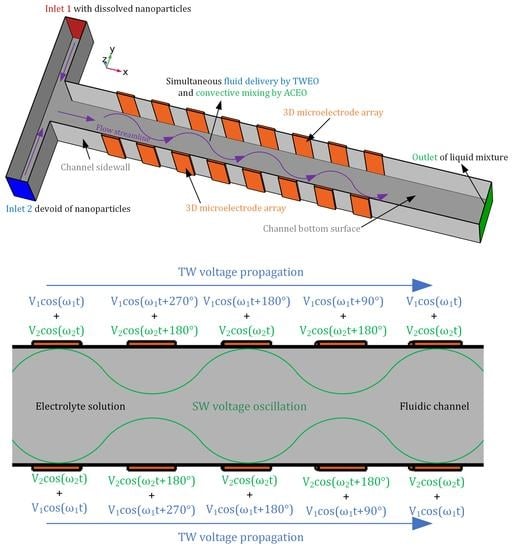
2.1. Geometry Configuration of the MICEO-Enabled Microfluidic Device for Simulations Study
2.2. Theory and Mathematical Model of Multi-Frequency ICEO
2.3. Numerical Simulation
3. Results and Discussion
3.1. Characterization of the ACEO Flow Component
3.2. TWEO Pump Behavior Driven by A Single Phase-Shifted Harmonic Field
3.3. Multi-Frequency ICEO from Combined ACEO and TWEO
3.4. Experimental Observation of MICEO Flow Field Above a Confocal Spiral Microelectrode Array
3.4.1. Device Configuration and Experimental Method
3.4.2. Experimental Results and Discussion
3.5. Influence of Electrolyte Conductivity and Channel Height on MICEO Streaming
3.6. Simulation Study of Simultaneous Pumping and Convective Mixing by MICEO
3.7. Advantages and Limitations of the Method of MICEO
3.8. Guidelines on the Usage of MICEO for Improving Real Microfluidic Systems
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Dittrich, P.S.; Tachikawa, K.; Manz, A. Micro total analysis systems. Latest advancements and trends. Anal. Chem. 2006, 78, 3887–3908. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.Y.; Chang, C.L.; Wang, Y.N.; Fu, L.M. Microfluidic mixing: A review. Int. J. Mol. Sci. 2011, 12, 3263–3278. [Google Scholar] [CrossRef] [PubMed]
- Squires, T.M.; Messinger, R.J.; Manalis, S.R. Making it stick: Convection, reaction and diffusion in surface-based biosensors. Nat. Biotechnol. 2008, 26, 417–426. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wang, G.; Lim, C.; Seong, G.H.; Choo, J.; Lee, E.K.; Kang, S.H.; Song, J.M. Evaluation of passive mixing behaviors in a pillar obstruction poly(dimethylsiloxane) microfluidic mixer using fluorescence microscopy. Microfluid. Nanofluid. 2009, 7, 267–273. [Google Scholar] [CrossRef]
- James, G.; Hold, A.E.; Arne, E.; Khan, A. A review of passive and active mixing systems in microfluidic devices. Int. J. Multiphys. 2009, 1, 1–32. [Google Scholar]
- Ramos, A. Electrokinetics and Electrohydrodynamics in Microsystems; Springer Science & Business Media: Berlin, Germany, 2011; Volume 530. [Google Scholar]
- Williams, S. Ac dielectrophoresis lab-on-chip devices. In Encyclopedia of Microfluidics and Nanofluidics; Springer: Berlin, Germany, 2008; pp. 1–8. [Google Scholar]
- Morgan, H.; Green, N.G. Ac Electrokinetics: Colloids and Nanoparticles; Research Studies Press: Philadelphia, PA, USA, 2003. [Google Scholar]
- Bazant, M.Z.; Thornton, K.; Ajdari, A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 2004, 70, 021506. [Google Scholar] [CrossRef] [Green Version]
- Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. Ac electrokinetics: A review of forces in microelectrode structures. J. Phys. D Appl. Phys. 1998, 31, 2338. [Google Scholar] [CrossRef]
- Castellanos, A.; Ramos, A.; Gonzalez, A.; Green, N.G.; Morgan, H. Electrohydrodynamics and dielectrophoresis in microsystems: Scaling laws. J. Phys. D Appl. Phys. 2003, 36, 2584. [Google Scholar] [CrossRef]
- Liu, W.; Ren, Y.; Tao, Y.; Chen, X.; Yao, B.; Hui, M.; Bai, L. Control of two-phase flow in microfluidics using out-of-phase electroconvective streaming. Phys. Fluids 2017, 29, 112002. [Google Scholar] [CrossRef]
- Liu, W.; Ren, Y.; Tao, Y.; Li, Y.; Chen, X. Controllable rotating behavior of individual dielectric microrod in a rotating electric field. Electrophoresis 2017, 38, 1427–1433. [Google Scholar] [CrossRef]
- Liu, W.; Ren, Y.; Tao, Y.; Yao, B.; Liu, N.; Wu, Q. A universal design of field-effect-tunable microfluidic ion diode based on a gating cation-exchange nanoporous membrane. Phys. Fluids 2017, 29, 112001. [Google Scholar] [CrossRef]
- Boymelgreen, A.M.; Balli, T.; Miloh, T.; Yossifon, G. Active colloids as mobile microelectrodes for unified label-free selective cargo transport. Nat. Commun. 2018, 9, 760. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.J. Ac electro-osmotic micropump by asymmetric electrode polarization. J. Appl. Phys. 2008, 103, 024907. [Google Scholar] [CrossRef]
- Ajdari, A. Pumping liquids using asymmetric electrode arrays. Phys. Rev. E 2000, 61, R45. [Google Scholar] [CrossRef]
- Kunti, G.; Bhattacharya, A.; Chakraborty, S. Analysis of micromixing of non-newtonian fluids driven by alternating current electrothermal flow. J. Non-Newton. Fluid Mech. 2017, 247, 123–131. [Google Scholar] [CrossRef]
- Kunti, G.; Bhattacharya, A.; Chakraborty, S. A scaling analysis for electrohydrodynamic convection with variable thermophysical and electrical properties. Int. J. Heat Mass Transf. 2017, 109, 215–222. [Google Scholar] [CrossRef]
- Green, N.G.; Ramos, A.; Gonzalez, A.; Castellanos, A.; Morgan, H. Electrothermally induced fluid flow on microelectrodes. J. Electrost. 2001, 53, 71–87. [Google Scholar] [CrossRef] [Green Version]
- Gimsa, J.; Stubbe, M.; Gimsa, U. A short tutorial contribution to impedance and ac-electrokinetic characterization and manipulation of cells and media: Are electric methods more versatile than acoustic and laser methods? J. Electr. Bioimpedance 2014, 5, 74–91. [Google Scholar] [CrossRef]
- Liu, W.; Ren, Y.; Shao, J.; Jiang, H.; Ding, Y. A theoretical and numerical investigation of travelling wave induction microfluidic pumping in a temperature gradient. J. Phys. D Appl. Phys. 2014, 47, 075501. [Google Scholar] [CrossRef]
- Liu, W.; Ren, Y.; Tao, Y.; Chen, X.; Wu, Q. Electrode cooling effect on out-of-phase electrothermal streaming in rotating electric fields. Micromachines 2017, 8, 327. [Google Scholar] [CrossRef]
- Park, S.; Yossifon, G. Electrothermal based active control of ion transport in a microfluidic device with an ion-permselective membrane. Nanoscale 2018, 10, 11633–11641. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Yang, K.; Wadhwa, A.; Eda, S.; Li, S.; Wu, J. Development of an ac electrokinetics-based immunoassay system for on-site serodiagnosis of infectious diseases. Sens. Actuators A Phys. 2011, 171, 406–413. [Google Scholar] [CrossRef]
- Park, S.; Koklu, M.; BeskoK, A. Particle trapping in high-conductivity media with electrothermally enhanced negative dielectrophoresis. Anal. Chem. 2009, 81, 2303–2310. [Google Scholar] [CrossRef] [PubMed]
- Lian, M.; Islam, N.; Wu, J. Ac electrothermal manipulation of conductive fluids and particles for lab-chip applications. IET Nanobiotechnol. 2007, 1, 36–43. [Google Scholar] [CrossRef] [PubMed]
- Green, N.G.; Ramos, A.; González, A.; Castellanos, A.; Morgan, H. Electric field induced fluid flow on microelectrodes: The effect of illumination. J. Phys. D Appl. Phys. 2000, 33, L13. [Google Scholar] [CrossRef]
- Stubbe, M.; Gyurova, A.; Gimsa, J. Experimental verification of an equivalent circuit for the characterization of electrothermal micropumps: High pumping velocities induced by the external inductance at driving voltages below 5 v. Electrophoresis 2013, 34, 562–574. [Google Scholar] [CrossRef]
- Williams, S.J. Enhanced electrothermal pumping with thin film resistive heaters. Electrophoresis 2013, 34, 1400–1408. [Google Scholar] [CrossRef]
- Kale, A.; Song, L.; Lu, X.; Yu, L.; Hu, G.; Xuan, X. Electrothermal enrichment of submicron particles in an insulator-based dielectrophoretic microdevice. Electrophoresis 2017, 39, 887–896. [Google Scholar] [CrossRef] [Green Version]
- Loire, S.; Kauffmann, P.; Mezić, I.; Meinhart, C. A theoretical and experimental study of ac electrothermal flows. J. Phys. D Appl. Phys. 2012, 45, 185301. [Google Scholar] [CrossRef]
- Iverson, B.D.; Garimella, S.V. Experimental characterization of induction electrohydrodynamics for integrated microchannel pumping. J. Micromech. Microeng. 2009, 19, 055015. [Google Scholar] [CrossRef]
- Felten, M.; Staroske, W.; Jaeger, M.S.; Schwille, P.; Duschl, C. Accumulation and filtering of nanoparticles in microchannels using electrohydrodynamically induced vortical flows. Electrophoresis 2008, 29, 2987–2996. [Google Scholar] [CrossRef] [PubMed]
- Du, E.; Manoochehri, S. Enhanced ac electrothermal fluidic pumping in microgrooved channels. J. Appl. Phys. 2008, 104, 064902. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.; Cheng, P.; Hong, F. A numerical study of an electrothermal vortex enhanced micromixer. Microfluid. Nanofluid. 2008, 5, 13–21. [Google Scholar] [CrossRef]
- Stubbe, M.; Holtappels, M.; Gimsa, J. A new working principle for ac electro-hydrodynamic on-chip micro-pumps. J. Phys. D Appl. Phys. 2007, 40, 6850. [Google Scholar] [CrossRef]
- Singhal, V.; Garimella, S.V. Induction electrohydrodynamics micropump for high heat flux cooling. Sens. Actuators A Phys. 2007, 134, 650–659. [Google Scholar] [CrossRef]
- Tao, Y.; Ren, Y.; Liu, W.; Wu, Y.; Jia, Y.; Lang, Q.; Jiang, H. Enhanced particle trapping performance of induced charge electroosmosis. Electrophoresis 2016, 37, 1326–1336. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, W.; Tao, Y.; Hui, M.; Wu, Q. On ac-field-induced nonlinear electroosmosis next to the sharp corner-field-singularity of leaky dielectric blocks and its application in on-chip micro-mixing. Micromachines 2018, 9, 102. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Q.; Ren, Y.; Cui, P.; Yao, B.; Li, Y.; Hui, M.; Jiang, T.; Bai, L. On the bipolar dc flow field-effect-transistor for multifunctional sample handing in microfluidics: A theoretical analysis under the debye–huckel limit. Micromachines 2018, 9, 82. [Google Scholar] [CrossRef]
- Liu, W.; Ren, Y.; Tao, Y.; Li, Y.; Wu, Q. On traveling-wave field-effect flow control for simultaneous induced-charge electroosmotic pumping and mixing in microfluidics: Physical perspectives and theoretical analysis. J. Micromech. Microeng. 2018, 28, 055004. [Google Scholar] [CrossRef]
- Squires, T.M.; Bazant, M.Z. Induced-charge electro-osmosis. J. Fluid Mech. 2004, 509, 217–252. [Google Scholar] [CrossRef] [Green Version]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena: Theory and microfluidic applications. Phys. Rev. Lett. 2004, 92, 066101. [Google Scholar] [CrossRef] [PubMed]
- Yossifon, G.; Frankel, I.; Miloh, T. Symmetry breaking in induced-charge electro-osmosis over polarizable spheroids. Phys. Fluids 2007, 19, 217. [Google Scholar] [CrossRef]
- Yossifon, G.; Frankel, I.; Miloh, T. On electro-osmotic flows through microchannel junctions. Phys. Fluids 2006, 18, 381. [Google Scholar] [CrossRef]
- Leinweber, F.C.; Eijkel, J.C.T.; Bower, J.G.; van den Berg, A. Continuous flow microfluidic demixing of electrolytes by induced charge electrokinetics in structured electrode arrays. Anal. Chem. 2006, 78, 1425–1434. [Google Scholar] [CrossRef] [PubMed]
- Squires, T.M. Induced-charge electrokinetics: Fundamental challenges and opportunities. Lab Chip 2009, 9, 2477–2483. [Google Scholar] [CrossRef] [PubMed]
- Gregersen, M.M.; Andersen, M.B.; Soni, G.; Meinhart, C.; Bruus, H. Numerical analysis of finite debye-length effects in induced-charge electro-osmosis. Phys. Rev. E 2009, 79, 066316. [Google Scholar] [CrossRef] [PubMed]
- Eckstein, Y.; Yossifon, G.; Seifert, A.; Miloh, T. Nonlinear electrokinetic phenomena around nearly insulated sharp tips in microflows. J. Colloid Interface Sci. 2009, 338, 243–249. [Google Scholar] [CrossRef]
- García-Sánchez, P.; Ramos, A. Electrorotation of a metal sphere immersed in an electrolyte of finite debye length. Phys. Rev. E 2015, 92, 052313. [Google Scholar] [CrossRef]
- Zehavi, M.; Yossifon, G. Particle dynamics and rapid trapping in electro-osmotic flow around a sharp microchannel corner. Phys. Fluids 2014, 26, 133–143. [Google Scholar] [CrossRef]
- Zehavi, M.; Boymelgreen, A.; Yossifon, G. Competition between induced-charge electro-osmosis and electrothermal effects at low frequencies around a weakly polarizable microchannel corner. Phys. Rev. Appl. 2016, 5, 044013. [Google Scholar] [CrossRef]
- Gimsa, J.; Eppmann, P.; Prüger, B. Introducing phase analysis light scattering for dielectric characterization: Measurement of traveling-wave pumping. Biophys. J. 1997, 73, 3309. [Google Scholar] [CrossRef]
- González, A.; Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. Electrothermal flows generated by alternating and rotating electric fields in microsystems. J. Fluid Mech. 2006, 564, 415–433. [Google Scholar] [CrossRef] [Green Version]
- Green, N.G.; Ramos, A.; González, A.; Morgan, H.; Castellanos, A. Fluid flow induced by nonuniform ac electric fields in electrolytes on microelectrodes. I. Experimental measurements. Phys. Rev. E 2000, 61, 4011. [Google Scholar] [CrossRef]
- González, A.; Ramos, A.; Green, N.G.; Castellanos, A.; Morgan, H. Fluid flow induced by nonuniform ac electric fields in electrolytes on microelectrodes. Ii. A linear double-layer analysis. Phys. Rev. E 2000, 61, 4019. [Google Scholar] [CrossRef]
- Green, N.G.; Ramos, A.; Gonzalez, A.; Morgan, H.; Castellanos, A. Fluid flow induced by nonuniform ac electric fields in electrolytes on microelectrodes. Iii. Observation of streamlines and numerical simulation. Phys. Rev. E 2002, 66, 026305. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Shao, J.; Ren, Y.; Liu, J.; Tao, Y.; Jiang, H.; Ding, Y. On utilizing alternating current-flow field effect transistor for flexibly manipulating particles in microfluidics and nanofluidics. Biomicrofluidics 2016, 10, 034105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, Y.; Liu, W.; Jia, Y.; Tao, Y.; Shao, J.; Ding, Y.; Jiang, H. Induced-charge electroosmotic trapping of particles. Lab Chip 2015, 15, 2181–2191. [Google Scholar] [CrossRef]
- Wu, J.; Ben, Y.; Chang, H.-C. Particle detection by electrical impedance spectroscopy with asymmetric-polarization ac electroosmotic trapping. Microfluid. Nanofluid. 2005, 1, 161–167. [Google Scholar] [CrossRef]
- Gonzalez, A.; Ramos, A.; García-Sánchez, P.; Castellanos, A. Effect of the combined action of faradaic currents and mobility differences in ac electro-osmosis. Phys. Rev. E 2010, 81, 016320. [Google Scholar] [CrossRef]
- Liu, W.; Shao, J.; Ren, Y.; Wu, Y.; Wang, C.; Ding, H.; Jiang, H.; Ding, Y. Effects of discrete-electrode arrangement on traveling-wave electroosmotic pumping. J. Micromech. Microeng. 2016, 26, 095003. [Google Scholar] [CrossRef]
- García-Sánchez, P.; Ramos, A.; Green, N.; Morgan, H. Traveling-wave electrokinetic micropumps: Velocity, electrical current, and impedance measurements. Langmuir 2008, 24, 9361–9369. [Google Scholar] [CrossRef] [PubMed]
- Ramos, A.; González, A.; García-Sánchez, P.; Castellanos, A. A linear analysis of the effect of faradaic currents on traveling-wave electroosmosis. J. Colloid Interface Sci. 2007, 309, 323–331. [Google Scholar] [CrossRef] [PubMed]
- Ramos, A.; Morgan, H.; Green, N.G.; González, A.; Castellanos, A. Pumping of liquids with traveling-wave electroosmosis. J. Appl. Phys. 2005, 97, 084906. [Google Scholar] [CrossRef] [Green Version]
- Cahill, B.P.; Heyderman, L.J.; Gobrecht, J.; Stemmer, A. Electro-osmotic streaming on application of traveling-wave electric fields. Phys. Rev. E 2004, 70, 036305. [Google Scholar] [CrossRef] [PubMed]
- Urdaneta, M.; Smela, E. Multiple frequency dielectrophoresis. Electrophoresis 2007, 28, 3145–3155. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Ren, Y.; Tao, Y.; Liu, W.; Jiang, T.; Jiang, H. Efficient micro-nano particle concentration using direct current induced thermal buoyancy convection for multiple liquid media. Anal. Chem. 2019, 91, 4457–4465. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Liu, W.; Ren, Y.; Hu, Y.; Li, G.; Ma, G.; Wu, Q. On developing field-effect-tunable nanofluidic ion diodes with bipolar, induced-charge electrokinetics. Micromachines 2018, 9, 179. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Ren, Y.; Liu, W.; Feng, X.; Hou, L.; Tao, Y.; Jiang, H. Flexible continuous particle beam switching via external-field-reconfigurable asymmetric induced-charge electroosmosis. Anal. Chem. 2018, 90, 11376–11384. [Google Scholar] [CrossRef]
- Canpolat, C.; Qian, S.; Beskok, A. Micro-piv measurements of induced-charge electro-osmosis around a metal rod. Microfluid. Nanofluid. 2013, 14, 153–162. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977. [Google Scholar] [CrossRef]
- Jain, M.; Yeung, A.; Nandakumar, K.J. Efficient micromixing using induced-charge electroosmosis. J. Microelectromech Syst. 2009, 18, 376–384. [Google Scholar] [CrossRef]
- Wu, Z.; Li, D. Micromixing using induced-charge electrokinetic flow. Electrochim. Acta 2008, 53, 5827–5835. [Google Scholar] [CrossRef]
- Zhao, H.; Bau, H.H. Microfluidic chaotic stirrer utilizing induced-charge electro-osmosis. Phys. Rev. E 2007, 75, 066217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Z.; Li, D. Mixing and flow regulating by induced-charge electrokinetic flow in a microchannel with a pair of conducting triangle hurdles. Microfluid. Nanofluid. 2008, 5, 65–76. [Google Scholar] [CrossRef]
- Zhang, F.; Daghighi, Y.; Li, D. Control of flow rate and concentration in microchannel branches by induced-charge electrokinetic flow. J. Colloid Interface Sci. 2011, 364, 588–593. [Google Scholar] [CrossRef] [PubMed]
- Jain, M.; Yeung, A.; Nandakumar, K. Induced charge electro osmotic mixer: Obstacle shape optimization. Biomicrofluidics 2009, 3, 022413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, Y.; Song, C.; Liu, W.; Jiang, T.; Song, J.; Wu, Q.; Jiang, H. On hybrid electroosmotic kinetics for field-effect-reconfigurable nanoparticle trapping in a four-terminal spiral microelectrode array. Electrophoresis 2019, 40, 979–992. [Google Scholar] [CrossRef]
- Prabhakaran, R.A.; Zhou, Y.; Zhao, C.; Hu, G.; Song, Y.; Wang, J.; Yang, C.; Xuan, X. Induced charge effects on electrokinetic entry flow. Phys. Fluids 2017, 29, 42–48. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schnitzer, O.; Yariv, E. Induced-charge electro-osmosis beyond weak fields. Phys. Rev. E 2012, 86, 061506. [Google Scholar] [CrossRef]
- Feng, X.; Ren, Y.; Jiang, H. An effective splitting-and-recombination micromixer with self-rotated contact surface for wide reynolds number range applications. Biomicrofluidics 2013, 7, 647. [Google Scholar] [CrossRef] [PubMed]











© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.; Song, J.; Liu, W.; Tao, Y.; Ren, Y. Multifrequency Induced-Charge Electroosmosis. Micromachines 2019, 10, 447. https://doi.org/10.3390/mi10070447
Du K, Song J, Liu W, Tao Y, Ren Y. Multifrequency Induced-Charge Electroosmosis. Micromachines. 2019; 10(7):447. https://doi.org/10.3390/mi10070447
Chicago/Turabian StyleDu, Kai, Jingni Song, Weiyu Liu, Ye Tao, and Yukun Ren. 2019. "Multifrequency Induced-Charge Electroosmosis" Micromachines 10, no. 7: 447. https://doi.org/10.3390/mi10070447
APA StyleDu, K., Song, J., Liu, W., Tao, Y., & Ren, Y. (2019). Multifrequency Induced-Charge Electroosmosis. Micromachines, 10(7), 447. https://doi.org/10.3390/mi10070447