Switchable Multifunctional Terahertz Metamaterials Based on the Phase-Transition Properties of Vanadium Dioxide
Abstract
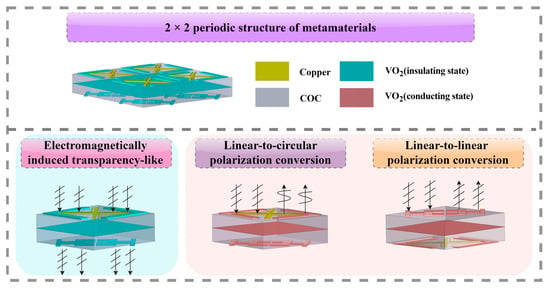
:1. Introduction
2. Structure Model
3. Electromagnetically Induced Transparency-like Effect of Metamaterials
4. Polarization Conversion Properties of Metamaterials
4.1. Simulation Results
4.2. Mechanism Analysis
4.3. Influence of Incidence Angle and Structural Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Harris, S.E.; Field, J.E.; Imamoglu, A. Nonlinear optical processes using electromagnetically induced transparency. Phys. Rev. Lett. 1990, 64, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Boller, K.; Imamolu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593–2596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, C.; Dutton, Z.; Behroozi, C.H.; Hau, L.V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 2001, 409, 490–493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidt, H.; Ram, R.J. All-optical wavelength converter and switch based on electromagnetically induced transparency. Appl. Phys. Lett. 2000, 76, 3173–3175. [Google Scholar] [CrossRef]
- Camacho, R.M.; Broadbent, C.J.; Ali-Khan, I.; Howell, J.C. All-optical delay of images using slow light. Phys. Rev. Lett. 2007, 98, 4. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 2008, 101, 47401. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Lang, T.T.; Hong, Z.; Shen, C.Y.; Shi, G.H. Comparison of Electromagnetically Induced Transparency Performance in Metallic and All-Dielectric Metamaterials. J. Lightwave Technol. 2018, 36, 2083–2093. [Google Scholar] [CrossRef]
- Cao, P.F.; Li, Y.; Wu, Y.Y.; Yuan, Z.N.; Li, S.L.; Cheng, L. Electromagnetically Induced Transparency-Like Terahertz Graphene Metamaterial with Tunable Carrier Mobility. IEEE Sens. J. 2021, 21, 14799–14806. [Google Scholar] [CrossRef]
- Chen, S.H.; Pan, T.S.; Peng, Y.Y.; Yao, G.; Gao, M.; Lin, Y. Analogue of Electromagnetically Induced Transparency Based on Bright-Bright Mode Coupling Between Spoof Electric Localized Surface Plasmon and Electric Dipole. IEEE Trans. Microw. Theory Tech. 2021, 69, 1538–1546. [Google Scholar] [CrossRef]
- Du, C.; Zhou, D.; Guo, H.H.; Pang, Y.Q.; Shi, H.Y.; Liu, W.F.; Singh, C.; Trukhanov, S.; Trukhanov, A.; Xu, Z. Active control scattering manipulation for realization of switchable EIT-like response metamaterial. Opt. Commun. 2021, 483, 5. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Wang, Y.; Yao, Y.; Tian, L.; Geng, Z.X.; Yang, Y.Q.; Jiang, J.X.; He, X.J. Active control of electromagnetically induced transparency based on terahertz hybrid metal-graphene metamaterials for slow light applications. Optik 2020, 200, 8. [Google Scholar] [CrossRef]
- Chen, J.X.; Wang, P.; Chen, C.C.; Lu, Y.H.; Ming, H.; Zhan, Q.W. Plasmonic EIT-like switching in bright-dark-bright plasmon resonators. Opt. Express. 2011, 19, 5970–5978. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Wang, C.; Qin, L.; Peng, R.W.; Xu, D.H.; Xiong, X.; Wang, M. Dual-mode electromagnetically induced transparency and slow light in a terahertz metamaterial. Opt. Lett. 2014, 39, 3539–3542. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Shao, Y.B.; Buyingaridi; Ma, S.; Gao, Y.C. Terahertz hybrid metal-graphene metamaterials with tunable dual-band electromagnetically induced transparency. Optik 2021, 240, 9. [Google Scholar] [CrossRef]
- Chauhan, V.S.; Manchaiah, D.; Kumar, P.; Kumar, R.; Bhushan, S.; Easwaran, R.K. Measurement of multi-frequency dispersions of Electromagnetically Induced Transparency windows using Spatial Light Modulator in rubidium vapor. Optik 2021, 225, 7. [Google Scholar] [CrossRef]
- Zografopoulos, D.C.; Swillam, M.; Beccherelli, R. Hybrid Plasmonic Modulators and Filters Based on Electromagnetically Induced Transparency. IEEE Photonics Technol. Lett. 2016, 28, 818–821. [Google Scholar] [CrossRef]
- Baghel, A.K.; Kulkarni, S.S.; Nayak, S.K. Linear-to-Cross-Polarization Transmission Converter Using Ultrathin and Smaller Periodicity Metasurface. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1433–1437. [Google Scholar] [CrossRef]
- Saqueb, S.A.N.; Sertel, K. Multisensor Compressive Sensing for High Frame-Rate Imaging System in the THz Band. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 520–523. [Google Scholar] [CrossRef]
- Gao, X.; Yang, W.L.; Ma, H.F.; Cheng, Q.; Yu, X.H.; Cui, T.J. A Reconfigurable Broadband Polarization Converter Based on an Active Metasurface. IEEE Trans. Antennas Propag. 2018, 66, 6086–6095. [Google Scholar] [CrossRef]
- Kapustina, O.A.; Kolesnikova, N.A. Liquid-crystalline polarization converter. Tech. Phys. Lett. 2001, 27, 74–76. [Google Scholar] [CrossRef]
- Doumanis, E.; Goussetis, G.; Dickie, R.; Cahill, R.; Baine, P.; Bain, M.; Fusco, V.; Encinar, J.A.; Toso, G. Electronically Reconfigurable Liquid Crystal Based Mm-Wave Polarization Converter. IEEE Trans. Antennas Propag. 2014, 62, 2302–2307. [Google Scholar] [CrossRef]
- Hao, J.M.; Yuan, Y.; Ran, L.X.; Jiang, T.; Kong, J.A.; Chan, C.T.; Zhou, L. Manipulating electromagnetic wave polarizations by anisotropic metamaterials. Phys. Rev. Lett. 2007, 99, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, Y.; Lin, H.; Koshelev, K.; Zhang, F.C.; Yang, Y.Y.; Wu, J.Y.; Kivshar, Y.; Jia, B.H. Full-Stokes Polarization Perfect Absorption with Diatomic Metasurfaces. Nano Lett. 2021, 21, 1090–1095. [Google Scholar] [CrossRef] [PubMed]
- Ji, C.Y.; Chen, S.S.; Han, Y.; Liu, X.; Liu, J.; Li, J.F.; Yao, Y.G. Artificial Propeller Chirality and Counterintuitive Reversal of Circular Dichroism in Twisted Meta-molecules. Nano Lett. 2021, 21, 6828–6834. [Google Scholar] [CrossRef] [PubMed]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.R.; Chen, H.T. Terahertz Metamaterials for Linear Polarization Conversion and Anomalous Refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef] [Green Version]
- Wen, Q.Y.; Zhang, H.W.; Yang, Q.H.; Xie, Y.S.; Chen, K.; Liu, Y.L. Terahertz metamaterials with VO2 cut-wires for thermal tunability. Appl. Phys. Lett. 2010, 97, 3. [Google Scholar] [CrossRef]
- Yao, Z.F.; Wei, T.T.; Wang, Y.K.; Lu, M.J.; Zhang, C.Y.; Zhang, L.L. Tunable multifunctional reflection polarizer based on a graphene metasurface. Appl. Opt. 2019, 58, 3570–3574. [Google Scholar] [CrossRef]
- Li, Y.R.; Luo, J.; Li, X.; Pu, M.B.; Ma, X.L.; Xie, X.; Shi, J.P.; Luo, X.G. Switchable Quarter-Wave Plate and Half-Wave Plate Based on Phase-Change Metasurface. IEEE Photonics J. 2020, 12, 10. [Google Scholar] [CrossRef]
- Song, Z.Y.; Zhang, J.H. Achieving broadband absorption and polarization conversion with a vanadium dioxide metasurface in the same terahertz frequencies. Opt. Express 2020, 28, 12487–12497. [Google Scholar] [CrossRef]
- Li, H.; Xu, W.H.; Cui, Q.; Wang, Y.; Yu, J. Theoretical design of a reconfigurable broadband integrated metamaterial terahertz device. Opt. Express 2020, 28, 40060–40074. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Qi, L.M.; Lan, F.; Lan, C.W.; Yang, J.; Tao, X. A VO2 film-based multifunctional metasurface in the terahertz band. Chin. Opt. Lett. 2022, 20, 7. [Google Scholar] [CrossRef]
- Wang, S.X.; Kang, L.; Werner, D.H. Hybrid Resonators and Highly Tunable Terahertz Metamaterials Enabled by Vanadium Dioxide (VO2). Sci. Rep. 2017, 7, 8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Xia, F.; Li, S.X.; Liu, Y.; Kong, W.J. Actively tunable multi-band terahertz perfect absorber due to the hybrid strong coupling in the multilayer structure. Opt. Express 2021, 29, 28619–28630. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.T.; Zhang, L.; Mukherjee, D.; Zheng, Y.X.; Haislmaier, R.C.; Alem, N.; Engel-Herbert, R. Wafer-scale growth of VO2 thin films using a combinatorial approach. Nat. Commun. 2015, 6, 8. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Xiang, T.Y.; Wu, J.; Yu, Z.T.; Yang, H.L. Tunable and polarization insensitive electromagnetically induced transparency using planar metamaterial. J. Magn. Magn. Mater. 2019, 476, 69–74. [Google Scholar] [CrossRef]
- Cong, L.Q.; Cao, W.; Zhang, X.Q.; Tian, Z.; Gu, J.Q.; Singh, R.; Han, J.G.; Zhang, W.L. A perfect metamaterial polarization rotator. Appl. Phys. Lett. 2013, 103, 5. [Google Scholar] [CrossRef]
- Zhang, J.R.; Zhang, K.; Cao, A.L.; Liu, Y.; Kong, W.J. Bi-functional switchable broadband terahertz polarization converter based on a hybrid graphene-metal metasurface. Opt. Express 2020, 28, 26102–26110. [Google Scholar] [CrossRef]
- Luo, J.; Shi, X.Z.; Luo, X.Q.; Hu, F.R.; Li, G.Y. Broadband switchable terahertz half-/quarter-wave plate based on metal-VO2 metamaterials. Opt. Express 2020, 28, 30861–30870. [Google Scholar] [CrossRef]
- Liu, Y.J.; Xia, S.; Shi, H.Y.; Zhang, A.X.; Xu, Z. Dual-band and high-efficiency polarization converter based on metasurfaces at microwave frequencies. Appl. Phys. B-Lasers Opt. 2016, 122, 8. [Google Scholar] [CrossRef]
- Gao, X.; Han, X.; Cao, W.P.; Li, H.O.; Ma, H.F.; Cui, T.J. Ultrawideband and High-Efficiency Linear Polarization Converter Based on Double V-Shaped Metasurface. IEEE Trans. Antennas Propag. 2015, 63, 3522–3530. [Google Scholar] [CrossRef]
- Wang, Z.J.; Jia, H.; Yao, K.; Cai, W.S.; Chen, H.S.; Liu, Y.M. Circular Dichroism Metamirrors with Near-Perfect Extinction. ACS Photonics 2016, 3, 2096–2101. [Google Scholar] [CrossRef]
- Wen, X.W.; Zheng, J.R. Broadband THz reflective polarization rotator by multiple plasmon resonances. Opt. Express 2014, 22, 28292–28300. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ishikawa, A.; Tanaka, T. Plasmon hybridization in graphene metamaterials. Appl. Phys. Lett. 2013, 102, 4. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Wang, X.; Wang, J.; Li, H.; Lu, Y.; Zhang, Y. Switchable Multifunctional Terahertz Metamaterials Based on the Phase-Transition Properties of Vanadium Dioxide. Micromachines 2022, 13, 1013. https://doi.org/10.3390/mi13071013
Sun Z, Wang X, Wang J, Li H, Lu Y, Zhang Y. Switchable Multifunctional Terahertz Metamaterials Based on the Phase-Transition Properties of Vanadium Dioxide. Micromachines. 2022; 13(7):1013. https://doi.org/10.3390/mi13071013
Chicago/Turabian StyleSun, Zhanshuo, Xin Wang, Junlin Wang, Hao Li, Yuhang Lu, and Yu Zhang. 2022. "Switchable Multifunctional Terahertz Metamaterials Based on the Phase-Transition Properties of Vanadium Dioxide" Micromachines 13, no. 7: 1013. https://doi.org/10.3390/mi13071013
APA StyleSun, Z., Wang, X., Wang, J., Li, H., Lu, Y., & Zhang, Y. (2022). Switchable Multifunctional Terahertz Metamaterials Based on the Phase-Transition Properties of Vanadium Dioxide. Micromachines, 13(7), 1013. https://doi.org/10.3390/mi13071013