Tunable Particle Focusing in a Straight Channel with Symmetric Semicircle Obstacle Arrays Using Electrophoresis-Modified Inertial Effects
Abstract
:1. Introduction
2. Theoretical Background
2.1. Inertial Lift Force
2.2. Electrophoresis
2.3. Dielectrophoresis
2.4. Saffman Force (Shear-Induced Lift Force)
3. Materials and Methods
3.1. Design and Fabrication of a Microfluidic Device
3.2. Particle Preparation
3.3. Experimental Setup
4. Results and Discussion
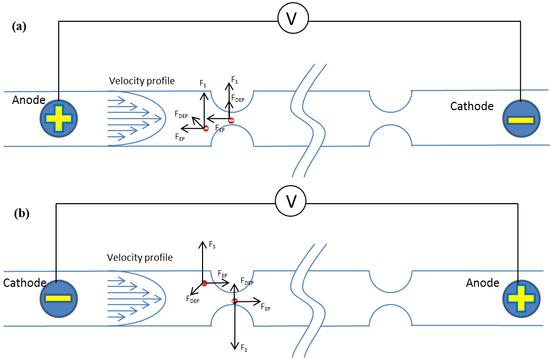
4.1. Schematic of Tunable Particle Focusing in the Straight Channel with Symmetric Semicircle Obstacle Arrays Using EP-Modified Inertial Effects
4.2. Effects of Electric Field Direction
4.3. Effects of Flow Rates
4.4. Effects of Electric Field Magnitude
4.5. Effects of Particle Size
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Bhagat, A.A.S.; Bow, H.; Hou, H.W.; Tan, S.J.; Han, J.; Lim, C.T. Microfluidics for cell separation. Med. Biol. Eng. Comput. 2010, 48, 999–1014. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, W.; Li, M.; Alici, G.; Nguyen, N.-T. Particle inertial focusing and its mechanism in a serpentine microchannel. Microfluid. Nanofluid. 2014, 17, 305–316. [Google Scholar] [CrossRef]
- Çetin, B.; Li, D. Dielectrophoresis in microfluidics technology. Electrophoresis 2011, 32, 2410–2427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forbes, T.P.; Forry, S.P. Microfluidic magnetophoretic separations of immunomagnetically labeled rare mammalian cells. Lab Chip 2012, 12, 1471–1479. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhe, J. Recent advances in particle and droplet manipulation for lab-on-a-chip devices based on surface acoustic waves. Lab Chip 2011, 11, 1280–1285. [Google Scholar] [CrossRef] [PubMed]
- Yamada, M.; Nakashima, M.; Seki, M. Pinched flow fractionation: Continuous size separation of particles utilizing a laminar flow profile in a pinched microchannel. Anal. Chem. 2004, 76, 5465–5471. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.R.; Cox, E.C.; Austin, R.H.; Sturm, J.C. Continuous particle separation through deterministic lateral displacement. Science 2004, 304, 987–990. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D. Inertial microfluidics. Lab Chip 2009, 9, 3038–3046. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yan, S.; Yuan, D.; Alici, G.; Nguyen, N.-T.; Warkiani, M.E.; Li, W. Fundamentals and applications of inertial microfluidics: A review. Lab Chip 2016, 16, 10–34. [Google Scholar] [CrossRef] [PubMed]
- Amini, H.; Lee, W.; Di Carlo, D. Inertial microfluidic physics. Lab Chip 2014, 14, 2739–2761. [Google Scholar] [CrossRef] [PubMed]
- Bhagat, A.A.S.; Kuntaegowdanahalli, S.S.; Papautsky, I. Continuous particle separation in spiral microchannels using dean flows and differential migration. Lab Chip 2008, 8, 1906–1914. [Google Scholar] [CrossRef] [PubMed]
- Kuntaegowdanahalli, S.S.; Bhagat, A.A.S.; Kumar, G.; Papautsky, I. Inertial microfluidics for continuous particle separation in spiral microchannels. Lab Chip 2009, 9, 2973–2980. [Google Scholar] [CrossRef] [PubMed]
- Warkiani, M.E.; Guan, G.; Luan, K.B.; Lee, W.C.; Bhagat, A.A.S.; Chaudhuri, P.K.; Tan, D.S.-W.; Lim, W.T.; Lee, S.C.; Chen, P.C. Slanted spiral microfluidics for the ultra-fast, label-free isolation of circulating tumor cells. Lab Chip 2014, 14, 128–137. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Guan, G.; Hou, H.W.; Bhagat, A.A.S.; Han, J. Separation of leukocytes from blood using spiral channel with trapezoid cross-section. Anal. Chem. 2012, 84, 9324–9331. [Google Scholar] [CrossRef] [PubMed]
- Kemna, E.W.; Schoeman, R.M.; Wolbers, F.; Vermes, I.; Weitz, D.A.; van den Berg, A. High-yield cell ordering and deterministic cell-in-droplet encapsulation using dean flow in a curved microchannel. Lab Chip 2012, 12, 2881–2887. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D.; Edd, J.F.; Irimia, D.; Tompkins, R.G.; Toner, M. Equilibrium separation and filtration of particles using differential inertial focusing. Anal. Chem. 2008, 80, 2204–2211. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yan, S.; Sluyter, R.; Li, W.; Alici, G.; Nguyen, N.-T. Inertial particle separation by differential equilibrium positions in a symmetrical serpentine micro-channel. Sci. Rep. 2014, 4, 4527. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.G.; Choi, S.; Park, J.-K. Three-dimensional hydrodynamic focusing with a single sheath flow in a single-layer microfluidic device. Lab Chip 2009, 9, 3155–3160. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.G.; Choi, S.; Kim, H.-J.; Lim, H.K.; Kim, J.-H.; Huh, N.; Park, J.-K. Inertial blood plasma separation in a contraction-expansion array microchannel. Appl. Phys. Lett. 2011, 98, 253702. [Google Scholar] [CrossRef]
- Lee, M.G.; Shin, J.H.; Bae, C.Y.; Choi, S.; Park, J.-K. Label-free cancer cell separation from human whole blood using inertial microfluidics at low shear stress. Anal. Chem. 2013, 85, 6213–6218. [Google Scholar] [CrossRef] [PubMed]
- Park, J.-S.; Song, S.-H.; Jung, H.-I. Continuous focusing of microparticles using inertial lift force and vorticity via multi-orifice microfluidic channels. Lab Chip 2009, 9, 939–948. [Google Scholar] [CrossRef] [PubMed]
- Yuan, D.; Zhang, J.; Sluyter, R.; Zhao, Q.; Yan, S.; Alici, G.; Li, W. Continuous plasma extraction under viscoelastic fluid in a straight channel with asymmetrical expansion–contraction cavity arrays. Lab Chip 2016, 16, 3919–3928. [Google Scholar] [CrossRef] [PubMed]
- Jeffrey, R.C.; Pearson, J. Particle motion in laminar vertical tube flow. J. Fluid Mech. 1965, 22, 721–735. [Google Scholar] [CrossRef]
- Repetti, R.; Leonard, E. Segré-silberberg annulus formation: A possible explanation. Nature 1964, 203, 1346–1348. [Google Scholar] [CrossRef]
- Kim, Y.W.; Yoo, J.Y. Axisymmetric flow focusing of particles in a single microchannel. Lab Chip 2009, 9, 1043–1045. [Google Scholar] [CrossRef] [PubMed]
- Asmolov, E.S. The inertial lift on a spherical particle in a plane poiseuille flow at large channel reynolds number. J. Fluid Mech. 1999, 381, 63–87. [Google Scholar] [CrossRef]
- Hunter, R.J. Foundations of Colloid Science; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Viovy, J.-L. Electrophoresis of DNA and other polyelectrolytes: Physical mechanisms. Rev. Mod. Phys. 2000, 72, 813. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Pohl, H. The Behavior of Neutral Matter in Nonuniform Electric Fields; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Jones, T.B.; Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Morgan, H.; Green, N. AC Electrokinetics: Colloids and Nanoparticles; Research Studies Press Ltd.: Hertfordshire, UK, 2003; p. 324. [Google Scholar]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Sollier, E.; Murray, C.; Maoddi, P.; Di Carlo, D. Rapid prototyping polymers for microfluidic devices and high pressure injections. Lab Chip 2011, 11, 3752–3765. [Google Scholar] [CrossRef] [PubMed]
- McDonald, J.C.; Whitesides, G.M. Poly(dimethylsiloxane) as a material for fabricating microfluidic devices. Acc. Chem. Res. 2002, 35, 491–499. [Google Scholar] [CrossRef] [PubMed]







© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, D.; Pan, C.; Zhang, J.; Yan, S.; Zhao, Q.; Alici, G.; Li, W. Tunable Particle Focusing in a Straight Channel with Symmetric Semicircle Obstacle Arrays Using Electrophoresis-Modified Inertial Effects. Micromachines 2016, 7, 195. https://doi.org/10.3390/mi7110195
Yuan D, Pan C, Zhang J, Yan S, Zhao Q, Alici G, Li W. Tunable Particle Focusing in a Straight Channel with Symmetric Semicircle Obstacle Arrays Using Electrophoresis-Modified Inertial Effects. Micromachines. 2016; 7(11):195. https://doi.org/10.3390/mi7110195
Chicago/Turabian StyleYuan, Dan, Chao Pan, Jun Zhang, Sheng Yan, Qianbin Zhao, Gursel Alici, and Weihua Li. 2016. "Tunable Particle Focusing in a Straight Channel with Symmetric Semicircle Obstacle Arrays Using Electrophoresis-Modified Inertial Effects" Micromachines 7, no. 11: 195. https://doi.org/10.3390/mi7110195
APA StyleYuan, D., Pan, C., Zhang, J., Yan, S., Zhao, Q., Alici, G., & Li, W. (2016). Tunable Particle Focusing in a Straight Channel with Symmetric Semicircle Obstacle Arrays Using Electrophoresis-Modified Inertial Effects. Micromachines, 7(11), 195. https://doi.org/10.3390/mi7110195