Three-Dimensional Force Measurements During Rapid Palatal Expansion in Sus scrofa
Abstract
:1. Introduction
2. Materials and Methods
2.1. Appliance Fabrication and Incorporation of Sensor
2.2. Force Relationships
2.3. Outcome Evaluation
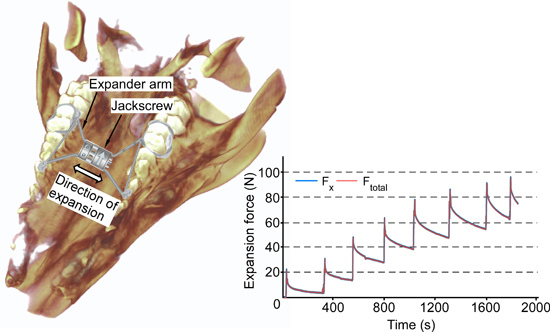
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Haas, A.J. Rapid expansion of the maxillary dental arch and nasal cavity by opening the midpalatal suture. Angle Orthod. 1961, 31, 73–90. [Google Scholar]
- Ghoneima, A.; Abdel-Fattah, E.; Eraso, F.; Fardo, D.; Kula, K.; Hartsfield, J. Skeletal and dental changes after rapid maxillary expansion: A computed tomography study. Aust. Orthod. J. 2010, 26, 141–148. [Google Scholar] [PubMed]
- Leonardi, R.; Cutrera, A.; Barbato, E. Rapid maxillary expansion affects the spheno-occipital synchondrosis in youngsters a study with low-dose computed tomography. Angle Orthod. 2010, 80, 106–110. [Google Scholar] [CrossRef] [PubMed]
- Nervina, J.M.; Kapila, S.D.; Mir, C.F. Assessment of maxillary transverse deficiency and treatment outcomes by cone-beam computed tomography. In Cone Beam Computed Tomography in Orthodontics: Indications, Insights and Innovations; Kapila, S., Ed.; Wiley-Blackwell: Ames, IA, USA, 2014; pp. 383–409. [Google Scholar]
- Ballanti, F.; Lione, R.; Fanucci, E.; Franchi, L.; Baccetti, T.; Cozza, P. Immediate and post-retention effects of rapid maxillary expansion investigated by computed tomography in growing patients. Angle Orthod. 2009, 79, 24–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garib, D.G.; Henriques, J.F.; Janson, G.; de Freitas, M.R.; Fernandes, A.Y. Periodontal effects of rapid maxillary expansion with tooth-tissue-borne and tooth-borne expanders: A computed tomography evaluation. Am. J. Orthod. Dentofac. Orthop. 2006, 129, 749–758. [Google Scholar] [CrossRef] [PubMed]
- Garrett, B.J.; Caruso, J.M.; Rungcharassaeng, K.; Farrage, J.R.; Kim, J.S.; Taylor, G.D. Skeletal effects to the maxilla after rapid maxillary expansion assessed with cone-beam computed tomography. Am. J. Orthod. Dentofac. Orthop. 2008, 134, 8–9. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, C.; Voyer, R.; Paquette, M.; Rompré, P.; Papadakis, A. Periodontal effects of surgically assisted rapid palatal expansion evaluated clinically and with cone-beam computerized tomography: 6-month preliminary results. Am. J. Orthod. Dentofac. Orthop. 2011, 139, S117–S128. [Google Scholar] [CrossRef] [PubMed]
- Kartalian, A.; Gohl, E.; Adamian, M.; Enciso, R. Cone-beam computerized tomography evaluation of the maxillary dentoskeletal complex after rapid palatal expansion. Am. J. Orthod. Dentofac. Orthop. 2010, 138, 486–492. [Google Scholar] [CrossRef] [PubMed]
- Harrison, J.E.; Ashby, D. Orthodontic treatment for posterior crossbites. Cochrane Database Syst. Rev. 2001, 1. [Google Scholar] [CrossRef]
- Schiffman, P.H.; Tuncay, O.C. Maxillary expansion: A meta analysis. Clin. Orthod. Res. 2001, 4, 86–96. [Google Scholar] [CrossRef] [PubMed]
- Zuccati, G.; Casci, S.; Doldo, T.; Clauser, C. Expansion of maxillary arches with crossbite: A systematic review of RCTs in the last 12 years. Eur. J. Orthod. 2013, 35, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Isaacson, R.J.; Wood, J.L.; Ingram, A.H. Forces produced by rapid maxillary expansion I. Design of the force measuring system. Angle Orthod. 1964, 34, 256–260. [Google Scholar]
- Isaacson, R.J.; Wood, J.L.; Ingram, A.H. Forces produced by rapid maxillary expansion II. Forces present during treatment. Angle Orthod. 1964, 34, 261–270. [Google Scholar]
- Zimring, J.F.; Isaacson, R.J. Forces produced by rapid maxillary expansion III. Forces present during retention. Angle Orthod. 1965, 35, 178–186. [Google Scholar] [PubMed]
- Papadaki, M.E.; Troulis, M.J.; Glowacki, J.; Kaban, L.B. A minipig model of maxillary distraction osteogenesis. J. Oral Maxillofac. Surg. 2010, 68, 2783–2791. [Google Scholar] [CrossRef] [PubMed]
- Stembirek, J.; Kyllar, M.; Putnová, I.; Stehlík, L.; Buchtová, M. The pig as an experimental model for clinical craniofacial research. Lab. Anim. 2012, 46, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Pepakayala, V.; Green, S.R.; Gianchandani, Y.B. Passive wireless strain sensors using microfabricated magnetoelastic beam elements. J. Microelectromech. Syst. 2014, 23, 1374–1382. [Google Scholar] [CrossRef]
- Masaki, T.; Kawata, K.; Masuzawa, T. Micro electro-discharge machining and its applications. In Proceedings of the IEEE Micro Electro Mechanical Systems, An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Napa Valley, CA, USA, 11–14 February 1990; pp. 21–26.
- Chen, G.; Ghaed, H.; Haque, R.u.; Wieckowski, M.; Kim, Y.; Kim, G.; Fick, D.; Kim, D.; Seok, M.; Wise, K.; Sylvester, D. A cubic-millimeter energy-autonomous wireless intraocular pressure monitor. In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 20–24 February 2011; pp. 138–139.
- Loeb, G.E.; Walker, A.E.; Uematsu, S.; Konigsmark, B.W. Histological reaction to various conductive and dielectric films chronically implanted in the subdural space. J. Biomed. Mater. Res. 1977, 11, 195–210. [Google Scholar] [CrossRef] [PubMed]






| Arm Number | Angle with xy Plane | Angle with xz Plane | Length (mm) |
|---|---|---|---|
| 1 | 29° | 21° | 13.8 |
| 2 | 21° | 29° | 12.3 |
| 3 | 24° | 33° | 16.5 |
| 4 | 25° | 43° | 16.9 |
| Cross section (all arms) | 1.2 × 1.2 mm2 | ||
| Young’s Modulus | Poisson’s Ratio | Density |
|---|---|---|
| 193 GPa | 0.27 | 8000 kg/m3 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goeckner, K.; Pepakayala, V.; Nervina, J.; Gianchandani, Y.; Kapila, S. Three-Dimensional Force Measurements During Rapid Palatal Expansion in Sus scrofa. Micromachines 2016, 7, 64. https://doi.org/10.3390/mi7040064
Goeckner K, Pepakayala V, Nervina J, Gianchandani Y, Kapila S. Three-Dimensional Force Measurements During Rapid Palatal Expansion in Sus scrofa. Micromachines. 2016; 7(4):64. https://doi.org/10.3390/mi7040064
Chicago/Turabian StyleGoeckner, Kelly, Venkatram Pepakayala, Jeanne Nervina, Yogesh Gianchandani, and Sunil Kapila. 2016. "Three-Dimensional Force Measurements During Rapid Palatal Expansion in Sus scrofa" Micromachines 7, no. 4: 64. https://doi.org/10.3390/mi7040064
APA StyleGoeckner, K., Pepakayala, V., Nervina, J., Gianchandani, Y., & Kapila, S. (2016). Three-Dimensional Force Measurements During Rapid Palatal Expansion in Sus scrofa. Micromachines, 7(4), 64. https://doi.org/10.3390/mi7040064