Hyperthermia Treatment Planning Including Convective Flow in Cerebrospinal Fluid for Brain Tumour Hyperthermia Treatment Using a Novel Dedicated Paediatric Brain Applicator
Abstract
:1. Introduction
2. Materials and Methods
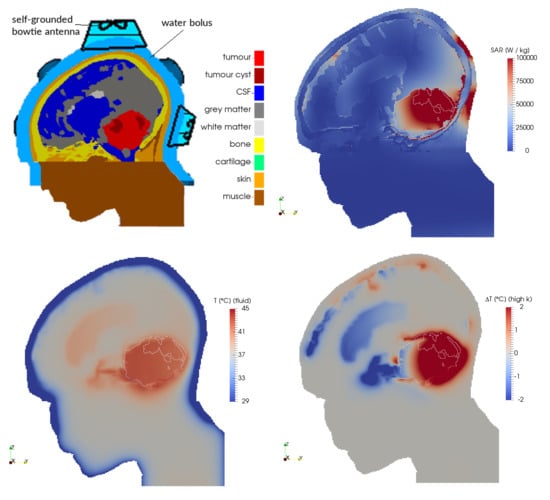
2.1. Patient Model and Electromagnetic Field Simulations
2.2. Temperature Simulations
- fluid: the CSF was modelled using fluid dynamics, including convective flow;
- solid: the CSF was modelled as a solid, similar to current practice in available hyperthermia treatment planning systems; and
- high-k: the CSF was modelled as a solid with an n-fold increased thermal conductivity keff, with keff/k = 2, 5, 10, 20, 50 and 100.
2.3. Analysis
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Overgaard, J.; González González, D.; Hulshof, M.C.; Arcangeli, G.; Dahl, O.; Mella, O.; Bentzen, S.M. Randomised trial of hyperthermia as adjuvant to radiotherapy for recurrent or metastatic malignant melanoma. European Society for Hyperthermic Oncology. Lancet 1995, 345, 540–543. [Google Scholar] [CrossRef]
- van der Zee, J.; González, D.; van Rhoon, G.C.; van Dijk, J.D.; van Putten, W.L.; Hart, A.A. Comparison of radiotherapy alone with radiotherapy plus hyperthermia in locally advanced pelvic tumours: A prospective, randomised, multicentre trial. Lancet 2000, 355, 1119–1125. [Google Scholar] [CrossRef]
- Datta, N.R.; Rogers, S.; Ordóñez, S.G.; Puric, E.; Bodis, S. Hyperthermia and radiotherapy in the management of head and neck cancers: A systematic review and meta-analysis. Int. J. Hyperth. 2016, 32, 31–40. [Google Scholar] [CrossRef] [PubMed]
- Datta, N.R.; Puric, E.; Klingbiel, D.; Gomez, S.; Bodis, S. Hyperthermia and Radiation Therapy in Locoregional Recurrent Breast Cancers: A Systematic Review and Meta-analysis. Int. J. Radiat. Oncol. Biol. Phys. 2016, 94, 1073–1087. [Google Scholar] [CrossRef] [PubMed]
- Wessalowski, R.; Schneider, D.T.; Mils, O.; Friemann, V.; Kyrillopoulou, O.; Schaper, J.; Matuschek, C.; Rothe, K.; Leuschner, I.; Willers, R.; et al. Regional deep hyperthermia for salvage treatment of children and adolescents with refractory or recurrent non-testicular malignant germ-cell tumours: An open-label, non-randomised, single-institution, phase 2 study. Lancet Oncol. 2013, 14, 843–852. [Google Scholar] [CrossRef]
- Liem, E.I.M.L.; Crezee, H.; de la Rosette, J.J.; de Reijke, T.M. Chemohyperthermia in non-muscle-invasive bladder cancer: An overview of the literature and recommendations. Int. J. Hyperth. 2016, 32, 363–373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Issels, R.D.; Lindner, L.H.; Verweij, J.; Wessalowski, R.; Reichardt, P.; Wust, P.; Ghadjar, P.; Hohenberger, P.; Angele, M.; Salat, C.; et al. Effect of Neoadjuvant Chemotherapy Plus Regional Hyperthermia on Long-term Outcomes Among Patients With Localized High-Risk Soft Tissue Sarcoma: The EORTC 62961-ESHO 95 Randomized Clinical Trial. JAMA Oncol. 2018, 4, 483–492. [Google Scholar] [CrossRef]
- Franckena, M.; Stalpers, L.J.A.; Koper, P.C.M.; Wiggenraad, R.G.J.; Hoogenraad, W.J.; van Dijk, J.D.P.; Wárlám-Rodenhuis, C.C.; Jobsen, J.J.; van Rhoon, G.C.; van der Zee, J. Long-Term Improvement in Treatment Outcome After Radiotherapy and Hyperthermia in Locoregionally Advanced Cervix Cancer: An Update of the Dutch Deep Hyperthermia Trial. Int. J. Radiat. Oncol. Biol. Phys. 2008, 70, 1176–1182. [Google Scholar] [CrossRef]
- Colombo, R.; Salonia, A.; Leib, Z.; Pavone-Macaluso, M.; Engelstein, D. Long-term outcomes of a randomized controlled trial comparing thermochemotherapy with mitomycin-C alone as adjuvant treatment for non-muscle-invasive bladder cancer (NMIBC). BJU Int. 2011, 107, 912–918. [Google Scholar] [CrossRef]
- van Dijk, I.W.E.M.; Cardous-Ubbink, M.C.; van der Pal, H.J.H.; Heinen, R.C.; van Leeuwen, F.E.; Oldenburger, F.; van Os, R.M.; Ronckers, C.M.; Schouten–van Meeteren, A.Y.N.; Caron, H.N.; et al. Dose-Effect Relationships for Adverse Events After Cranial Radiation Therapy in Long-term Childhood Cancer Survivors. Int. J. Radiat. Oncol. Biol. Phys. 2013, 85, 768–775. [Google Scholar] [CrossRef]
- Vujaskovic, Z.; Song, C.W. Physiological mechanisms underlying heat-induced radiosensitization. Int. J. Hyperth. 2004, 20, 163–174. [Google Scholar] [CrossRef] [PubMed]
- van Leeuwen, C.M.; Crezee, J.; Oei, A.L.; Franken, N.A.P.; Stalpers, L.J.A.; Bel, A.; Kok, H.P. 3D radiobiological evaluation of combined radiotherapy and hyperthermia treatments. Int. J. Hyperth. 2017, 33, 160–169. [Google Scholar] [CrossRef] [PubMed]
- Van Tellingen, O.; Yetkin-Arik, B.; de Gooijer, M.C.; Wesseling, P.; Wurdinger, T.; de Vries, H.E. Overcoming the blood–brain tumor barrier for effective glioblastoma treatment. Drug Resist. Updates 2015, 19, 12. [Google Scholar] [CrossRef] [PubMed]
- Leuthardt, E.C.; Duan, C.; Kim, M.J.; Campian, J.L.; Kim, A.H.; Miller-Thomas, M.M.; Shimony, J.S.; Tran, D.D. Hyperthermic Laser Ablation of Recurrent Glioblastoma Leads to Temporary Disruption of the Peritumoral Blood Brain Barrier. PLoS ONE 2016, 11, e0148613. [Google Scholar] [CrossRef] [PubMed]
- Bredlau, A.L.; Motamarry, A.; Chen, C.; McCrackin, M.A.; Helke, K.; Armeson, K.E.; Bynum, K.; Broome, A.-M.; Haemmerich, D. Localized delivery of therapeutic doxorubicin dose across the canine blood-brain barrier with hyperthermia and temperature sensitive liposomes. Drug Deliv. 2018, 25, 973–984. [Google Scholar] [CrossRef] [PubMed]
- Kiyatkin, E.A.; Sharma, H.S. Permeability of the blood–brain barrier depends on brain temperature. Neuroscience 2009, 161, 926–939. [Google Scholar] [CrossRef] [PubMed]
- Moriyama, E.; Salcman, M.; Broadwell, R.D. Blood-brain barrier alteration after microwave-induced hyperthermia is purely a thermal effect: I. Temperature and power measurements. Surg. Neurol. 1991, 35, 177–182. [Google Scholar] [CrossRef]
- Sneed, P.K.; Stauffer, P.R.; McDermott, M.W.; Diederich, C.J.; Lamborn, K.R.; Prados, M.D.; Chang, S.; Weaver, K.A.; Spry, L.; Malec, M.K.; et al. Survival benefit of hyperthermia in a prospective randomized trial of brachytherapy boost +/- hyperthermia for glioblastoma multiforme. Int. J. Radiat. Oncol. Biol. Phys. 1998, 40, 287–295. [Google Scholar] [CrossRef]
- Hulshof, M.C.C.M.; Raaymakers, B.W.; Lagendijk, J.J.W.; Koot, R.W.; Crezee, H.; Stalpers, L.J.A.; González González, D. A feasibility study of interstitial hyperthermia plus external beam radiotherapy in glioblastoma multiforme using the multi electrode current source (MECS) system. Int. J. Hyperth. 2004, 20, 451–463. [Google Scholar] [CrossRef]
- Maier-Hauff, K.; Ulrich, F.; Nestler, D.; Niehoff, H.; Wust, P.; Thiesen, B.; Orawa, H.; Budach, V.; Jordan, A. Efficacy and safety of intratumoral thermotherapy using magnetic iron-oxide nanoparticles combined with external beam radiotherapy on patients with recurrent glioblastoma multiforme. J. Neuro-Oncol. 2011, 103, 317–324. [Google Scholar] [CrossRef]
- Mahmoudi, K.; Bouras, A.; Bozec, D.; Ivkov, R.; Hadjipanayis, C. Magnetic hyperthermia therapy for the treatment of glioblastoma: A review of the therapy’s history, efficacy and application in humans. Int. J. Hyperth. 2018, 34, 1316–1328. [Google Scholar] [CrossRef] [PubMed]
- Byun, Y.H.; Gwak, H.S.; Kwon, J.-W.; Song, M.K.; Shin, S.H.; Jo, Y.H.; Yoo, H.; Lee, S.H. Local recurrence of brain metastasis reduced by intra-operative hyperthermia treatment. Int. J. Hyperth. 2018, 35, 168–175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharma, H.S.; Hoopes, P.J. Hyperthermia induced pathophysiology of the central nervous system. Int. J. Hyperth. 2003, 19, 325–354. [Google Scholar] [CrossRef] [PubMed]
- Haveman, J.; Sminia, P.; Wondergem, J.; van der Zee, J.; Hulshof, M.C.C.M. Effects of hyperthermia on the central nervous system: What was learnt from animal studies? Int. J. Hyperth. 2005, 21, 473–487. [Google Scholar] [CrossRef] [PubMed]
- Bredlau, A.L.; McCrackin, M.A.; Motamarry, A.; Helke, K.; Chen, C.; Broome, A.-M.; Haemmerich, D. Thermal Therapy Approaches for Treatment of Brain Tumors in Animals and Humans. Crit. Rev. Biomed. Eng. 2016, 44, 443–457. [Google Scholar] [CrossRef] [PubMed]
- Bing, C.; Ladouceur-Wodzak, M.; Wanner, C.R.; Shelton, J.M.; Richardson, J.A.; Chopra, R. Trans-cranial opening of the blood-brain barrier in targeted regions using a stereotaxic brain atlas and focused ultrasound energy. J. Ther. Ultrasound 2014, 2, 13. [Google Scholar] [CrossRef] [PubMed]
- Maloney, E.; Hwang, J.H. Emerging HIFU applications in cancer therapy. Int. J. Hyperth. 2015, 31, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Mainprize, T.; Lipsman, N.; Huang, Y.; Meng, Y.; Bethune, A.; Ironside, S.; Heyn, C.; Alkins, R.; Trudeau, M.; Sahgal, A.; et al. Blood-Brain Barrier Opening in Primary Brain Tumors with Non-invasive MR-Guided Focused Ultrasound: A Clinical Safety and Feasibility Study. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef] [PubMed]
- Rutkowski, S.; Bode, U.; Deinlein, F.; Ottensmeier, H.; Warmuth-Metz, M.; Soerensen, N.; Graf, N.; Emser, A.; Pietsch, T.; Wolff, J.E.A.; et al. Treatment of early childhood medulloblastoma by postoperative chemotherapy alone. N. Engl. J. Med. 2005, 352, 978–986. [Google Scholar] [CrossRef]
- Duffner, P.K. Long-term effects of radiation therapy on cognitive and endocrine function in children with leukemia and brain tumors. Neurologist 2004, 10, 293–310. [Google Scholar] [CrossRef]
- Smoll, N.R. Relative survival of childhood and adult medulloblastomas and primitive neuroectodermal tumors (PNETs). Cancer 2012, 118, 1313–1322. [Google Scholar] [CrossRef] [PubMed]
- Saad, S.; Wang, T.J.C. Neurocognitive Deficits After Radiation Therapy for Brain Malignancies. Am. J. Clin. Oncol. 2015, 38, 634–640. [Google Scholar] [CrossRef] [PubMed]
- Mulder, R.L.; Kremer, L.C.M.; van Santen, H.M.; Ket, J.L.; van Trotsenburg, A.S.P.; Koning, C.C.E.; Schouten-van Meeteren, A.Y.N.; Caron, H.N.; Neggers, S.J.C.M.M.; van Dalen, E.C. Prevalence and risk factors of radiation-induced growth hormone deficiency in childhood cancer survivors: A systematic review. Cancer Treat. Rev. 2009, 35, 616–632. [Google Scholar] [CrossRef] [PubMed]
- Uday, S.; Murray, R.D.; Picton, S.; Chumas, P.; Raju, M.; Chandwani, M.; Alvi, S. Endocrine sequelae beyond 10 years in survivors of medulloblastoma. Clin. Endocrinol. 2015, 83, 663–670. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; Crezee, J.; Franken, N.A.P.; Stalpers, L.J.A.; Barendsen, G.W.; Bel, A. Quantifying the combined effect of radiation therapy and hyperthermia in terms of equivalent dose distributions. Int. J. Radiat. Oncol. Biol. Phys. 2014, 88, 739–745. [Google Scholar] [CrossRef]
- Michiels, E.M.; Schouten-Van Meeteren, A.Y.; Doz, F.; Janssens, G.O.; van Dalen, E.C. Chemotherapy for children with medulloblastoma. Cochrane Database Syst. Rev. 2015. [Google Scholar] [CrossRef] [PubMed]
- Dobšíček Trefná, H.; Togni, P.; Shiee, R.; Vrba, J.; Persson, M. Design of a wideband multi-channel system for time reversal hyperthermia. Int. J. Hyperth. 2012, 28, 175–183. [Google Scholar] [CrossRef] [Green Version]
- Dobšíček Trefná, H.; Kok, H.P.; Takook, P.; Gellermann, J.; Lannering, B.; Blomgren, K.; Crezee, H.; Persson, M. EP-1271: Development of focused microwave hyperthermia of pediatric brain cancer. Radiother. Oncol. 2015, 115, S685–S686. [Google Scholar] [CrossRef]
- Takook, P.; Persson, M.; Gellermann, J.; Dobšíček Trefná, H. Compact self-grounded Bow-Tie antenna design for an UWB phased-array hyperthermia applicator. Int. J. Hyperth. 2017, 33, 387–400. [Google Scholar] [CrossRef]
- Takook, P.; Persson, M.; Dobšíček Trefná, H. Performance Evaluation of Hyperthermia Applicators to Heat Deep-Seated Brain Tumors. IEEE J. Electromagn. RF Microw. Med. Biol. 2018, 2, 18–24. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1998, 85, 5–34. [Google Scholar] [CrossRef] [PubMed]
- Kotte, A.; van Leeuwen, G.; de Bree, J.; van der Koijk, J.; Crezee, H.; Lagendijk, J. A description of discrete vessel segments in thermal modelling of tissues. Phys. Med. Biol. 1996, 41, 865–884. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; Gellermann, J.; van den Berg, C.A.T.; Stauffer, P.R.; Hand, J.W.; Crezee, J. Thermal modelling using discrete vasculature for thermal therapy: A review. Int. J. Hyperth. 2013, 29, 336–345. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; Kotte, A.N.T.J.; Crezee, J. Planning, optimisation and evaluation of hyperthermia treatments. Int. J. Hyperth. 2017, 33, 593–607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schooneveldt, G.; Kok, H.P.; Geijsen, E.D.; van Ommen, F.; Bakker, A.; Zanartu, M.A.W.; de la Rosette, J.J.M.C.H.; Hulshof, M.C.C.M.; de Reijke, T.M.; Crezee, J. Improved temperature monitoring and treatment planning for loco-regional hyperthermia treatments of Non-Muscle Invasive Bladder Cancer (NMIBC). In World Congress on Medical Physics and Biomedical Engineering, Toronto, ON, Canada, 7–12 June 2015; Jaffray, D.A., Ed.; Springer International Publishing: Cham, Switzerland, 2015; Volume 51, pp. 1691–1694. ISBN 978-3-319-19386-1. [Google Scholar]
- Schooneveldt, G.; Kok, H.P.; Balidemaj, E.; Geijsen, E.D.; van Ommen, F.; Sijbrands, J.; Bakker, A.; de la Rosette, J.J.M.C.H.; Hulshof, M.C.C.M.; de Reijke, T.M.; et al. Improving hyperthermia treatment planning for the pelvis by accurate fluid modeling. Med. Phys. 2016, 43, 5442. [Google Scholar] [CrossRef] [PubMed]
- Schooneveldt, G.; Löke, D.R.; Zweije, R.; Helderman, R.F.C.P.A.; Kok, H.P.; Crezee, H. Experimental validation of a thermophysical fluid model designed to improve the Hyperthermia Treatment Planning near fluid regions. Int. J. Heat Mass Trans. 2019. submitted. [Google Scholar]
- Schooneveldt, G.; Kok, H.P.; Bakker, A.; Geijsen, E.D.; Rasch, C.R.N.; de la Rosette, J.J.M.C.H.; Hulshof, M.C.C.M.; de Reijke, T.M.; Crezee, H. Clinical validation of a novel thermophysical bladder model designed to improve the accuracy of hyperthermia treatment planning in the pelvic region. Int. J. Hyperth. 2018, 35, 383–397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schooneveldt, G.; Kok, H.P.; Bakker, A.; Geijsen, E.D.; Hulshof, M.C.C.M.; de Reijke, T.M.; Crezee, J. The effect of air pockets in the urinary bladder on the temperature distribution during loco-regional hyperthermia treatment of bladder cancer patients. Int. J. Hyperth. 2018, 35, 441–449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- IT’IS Foundation. Tissue Properties Database. V3.1. 2016. Available online: https://itis.swiss/virtual-population/tissue-properties/downloads/database-v3-1/ (accessed on 7 June 2018).
- Gabriel, C.; Gabriel, S. Compilation of the Dielectrical Properties of Body Tissues at RF and Microwave Frequencies; Armstrong Laboratory, Brooks Air Force Base Texas: San Antonio, TX, USA, 1996. [Google Scholar]
- Wang, Z.; Lin, J.C.; Mao, W.; Liu, W.; Smith, M.B.; Collins, C.M. SAR and temperature: Simulations and comparison to regulatory limits for MRI. J. Magn. Reson. Imaging 2007, 26, 437–441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kok, H.P.; van Haaren, P.M.A.; van Dijk, J.D.P.; Crezee, J. On estimation of the temperature maximum in intraluminal or intracavitary hyperthermia. Int. J. Hyperth. 2005, 21, 287–304. [Google Scholar] [CrossRef]
- Dobšíček Trefná, H.; Jonsson, J.; Vessman, B.; Wanemark, J.; Woxlin, E.; Hjalmarson, A.; Adelback, L.; Gellermann, J.; Takook, P.; Lannering, B.; et al. Antenna applicator for microwave hyperthermia treatment of pediatric brain cancer. In Proceedings of the 2014 8th European Conference on Antennas and Propagation (EuCAP 2014), Hague, The Netherlands, 6–11 April 2014; European Association on Antennas and Propagation, Ed.; IEEE: Piscataway, NJ, USA, 2014. ISBN 978-88-907018-4-9. [Google Scholar]
- Dobšíček Trefná, H.; Vrba, J.; Persson, M. Time-reversal focusing in microwave hyperthermia for deep-seated tumors. Phys. Med. Biol. 2010, 55, 2167–2185. [Google Scholar] [CrossRef] [PubMed]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620. [Google Scholar] [CrossRef]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM®; Holzmann CFD: 2017. Available online: https://holzmann-cfd.de/publications/mathematics-numerics-derivations-and-openfoam (accessed on 1 August 2018).
- Yuan, Y.; Cheng, K.-S.; Craciunescu, O.I.; Stauffer, P.R.; Maccarini, P.F.; Arunachalam, K.; Vujaskovic, Z.; Dewhirst, M.W.; Das, S.K. Utility of treatment planning for thermochemotherapy treatment of nonmuscle invasive bladder carcinoma. Med. Phys. 2012, 39, 1170. [Google Scholar] [CrossRef] [PubMed]
- Weinbaum, S.; Jiji, L.M. A New Simplified Bioheat Equation for the Effect of Blood Flow on Local Average Tissue Temperature. J. Biomech. Eng. 1985, 107, 131. [Google Scholar] [CrossRef] [PubMed]
- Crezee, J.; Mooibroek, J.; Lagendijk, J.J.; van Leeuwen, G.M. The theoretical and experimental evaluation of the heat balance in perfused tissue. Phys. Med. Biol. 1994, 39, 813–832. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stoll, A.M.; Greene, L.C. Relationship between pain and tissue damage due to thermal radiation. J. Appl. Physiol. 1959, 14, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; Korshuize-van Straten, L.; Bakker, A.; de Kroon-Oldenhof, R.; Geijsen, E.D.; Stalpers, L.J.A.; Crezee, J. Online Adaptive Hyperthermia Treatment Planning During Locoregional Heating to Suppress Treatment-Limiting Hot Spots. Int. J. Radiat. Oncol. Biol. Phys. 2017, 99, 1039–1047. [Google Scholar] [CrossRef] [PubMed]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Lyons, B.E.; Samulski, T.V.; Cox, R.S.; Fessenden, P. Heat loss and blood flow during hyperthermia in normal canine brain. I: Empirical study and analysis. Int. J. Hyperth. 1989, 5, 225–247. [Google Scholar] [CrossRef]
- Satoh, T.; Nakasone, S.; Nishimoto, A. Cerebral blood flow response to the tissue temperature in tumour and brain tissues. Int. J. Hyperth. 1989, 5, 683–696. [Google Scholar] [CrossRef]
- Moriyama, E. Cerebral blood flow changes during localized hyperthermia. Neurol. Med. Chir. (Tokyo) 1990, 30, 923–929. [Google Scholar] [CrossRef] [PubMed]
- Oberacker, E.; Kuehne, A.; Nadobny, J.; Zschaeck, S.; Weihrauch, M.; Waiczies, H.; Ghadjar, P.; Wust, P.; Niendorf, T.; Winter, L. Radiofrequency applicator concepts for simultaneous MR imaging and hyperthermia treatment of glioblastoma multiforme. Curr. Dir. Biomed. Eng. 2017, 3. [Google Scholar] [CrossRef]
- Turner, P.F.; Ellsworth, J. Apparatus and Method for Creating Small Focus Deep Hyperthermia in Tissues of the Brain 2019. Patent Application US2019/0030354 A1, 31 January 2019. [Google Scholar]
- Verduijn, G.M.; de Wee, E.M.; Rijnen, Z.; Togni, P.; Hardillo, J.A.U.; ten Hove, I.; Franckena, M.; van Rhoon, G.C.; Paulides, M.M. Deep hyperthermia with the HYPERcollar system combined with irradiation for advanced head and neck carcinoma—A feasibility study. Int. J. Hyperth. 2018, 34, 994–1001. [Google Scholar] [CrossRef] [PubMed]
- Rijnen, Z.; Togni, P.; Roskam, R.; van de Geer, S.G.; Goossens, R.H.M.; Paulides, M.M. Quality and comfort in head and neck hyperthermia: A redesign according to clinical experience and simulation studies. Int. J. Hyperth. 2015, 31, 823–830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verhaart, R.F.; Rijnen, Z.; Fortunati, V.; Verduijn, G.M.; van Walsum, T.; Veenland, J.F.; Paulides, M.M. Temperature simulations in hyperthermia treatment planning of the head and neck region: Rigorous optimization of tissue properties. Strahlenther. Onkol. 2014, 190, 1117–1124. [Google Scholar] [CrossRef] [PubMed]
- Verhaart, R.F.; Verduijn, G.M.; Fortunati, V.; Rijnen, Z.; van Walsum, T.; Veenland, J.F.; Paulides, M.M. Accurate 3D temperature dosimetry during hyperthermia therapy by combining invasive measurements and patient-specific simulations. Int. J. Hyperth. 2015, 31, 686–692. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schooneveldt, G.; Bakker, A.; Balidemaj, E.; Chopra, R.; Crezee, J.; Geijsen, E.D.; Hartmann, J.; Hulshof, M.C.C.M.; Kok, H.P.; Paulides, M.M.; et al. Thermal dosimetry for bladder hyperthermia treatment. An overview. Int. J. Hyperth. 2016, 32, 417–433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kothapalli, S.V.V.N.; Altman, M.B.; Zhu, L.; Partanen, A.; Cheng, G.; Gach, H.M.; Straube, W.; Zoberi, I.; Hallahan, D.E.; Chen, H. Evaluation and selection of anatomic sites for magnetic resonance imaging-guided mild hyperthermia therapy: A healthy volunteer study. Int. J. Hyperth. 2018, 34, 1381–1389. [Google Scholar] [CrossRef]
- Balidemaj, E.; Kok, H.P.; Schooneveldt, G.; van Lier, A.L.H.M.W.; Remis, R.F.; Stalpers, L.J.A.; Westerveld, H.; Nederveen, A.J.; van den Berg, C.A.T.; Crezee, J. Hyperthermia treatment planning for cervical cancer patients based on electrical conductivity tissue properties acquired in vivo with EPT at 3 T MRI. Int. J. Hyperth. 2016, 32, 558–568. [Google Scholar] [CrossRef]












| Tissue Type | σ (S/m) | εr (–) | ρ (kg/m3) | Ct (J/(kg K)) | k (W/(m K)) | ω Cb (W/(m3 K)) | Flow |
|---|---|---|---|---|---|---|---|
| tumour | 0.84 | 56.64 | 1056 | 3700 | 0.57 | 22,545 | no |
| tumour cyst | 0.84 | 56.64 | 1056 | 3700 | 0.57 | 0 | no |
| cerebrospinal fluid | 2.28 | 70.95 | 1007 | 4200 | 0.62 | 0 | yes |
| grey matter | 0.76 | 56.48 | 1038 | 3700 | 0.57 | 45,090 | no |
| white matter | 0.46 | 41.43 | 1038 | 3600 | 0.50 | 15,925 | no |
| muscle | 0.93 | 75 | 1050 | 3639 | 0.56 | 12,960 | no |
| bone | 0.095 | 13.03 | 1990 | 1300 | 0.40 | 3400 | no |
| cartilage | 0.60 | 44.94 | 1097 | 3500 | 0.47 | 9000 | no |
| skin | 0.71 | 45.70 | 1125 | 3500 | 0.42 | 8065 | no |
| vitreous humour | 1.54 | 69.00 | 1009 | 4200 | 0.60 | 0 | no |
| air | 0 | 1 | 1.293 | 10,000 | 0.024 | 0 | no |
| bolus water | 0.070 | 83.83 | 1000 | 4180 | 0.60 | 0 | no |
| Case | Region | Parameter | Fluid | Solid | 2 k | 5 k | 10 k | 20 k | 50 k | 100 k |
|---|---|---|---|---|---|---|---|---|---|---|
| pre-op | solid | volume | 22.31 | 36.46 | 30.45 | 24.84 | 22.29 | 20.55 | 17.43 | 14.26 |
| overlap | 22.31 | 20.00 | 19.29 | 17.71 | 16.88 | 16.42 | 15.11 | 13.14 | ||
| Dice | 1.00 | 0.68 | 0.73 | 0.75 | 0.76 | 0.77 | 0.76 | 0.72 | ||
| CSF | volume | 23.94 | 29.37 | 21.39 | 16.12 | 13.20 | 12.61 | 12.57 | 11.68 | |
| overlap | 23.94 | 17.08 | 15.15 | 12.69 | 11.30 | 11.56 | 11.62 | 10.78 | ||
| Dice | 1.00 | 0.64 | 0.67 | 0.63 | 0.61 | 0.63 | 0.64 | 0.61 | ||
| total | volume | 46.25 | 65.83 | 51.85 | 40.96 | 35.49 | 33.17 | 29.99 | 25.94 | |
| overlap | 46.25 | 37.08 | 34.45 | 30.40 | 28.18 | 27.99 | 26.73 | 23.91 | ||
| Dice | 1.00 | 0.66 | 0.70 | 0.70 | 0.69 | 0.70 | 0.70 | 0.66 | ||
| post-op | solid | volume | 0.23 | 19.76 | 17.37 | 14.33 | 10.59 | 5.60 | 0.64 | 0 |
| CSF | volume | 2.74 | 125.11 | 120.91 | 112.89 | 103.80 | 84.28 | 24.95 | 0 | |
| total | volume | 2.97 | 144.87 | 138.27 | 127.22 | 114.38 | 89.88 | 25.59 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schooneveldt, G.; Dobšíček Trefná, H.; Persson, M.; de Reijke, T.M.; Blomgren, K.; Kok, H.P.; Crezee, H. Hyperthermia Treatment Planning Including Convective Flow in Cerebrospinal Fluid for Brain Tumour Hyperthermia Treatment Using a Novel Dedicated Paediatric Brain Applicator. Cancers 2019, 11, 1183. https://doi.org/10.3390/cancers11081183
Schooneveldt G, Dobšíček Trefná H, Persson M, de Reijke TM, Blomgren K, Kok HP, Crezee H. Hyperthermia Treatment Planning Including Convective Flow in Cerebrospinal Fluid for Brain Tumour Hyperthermia Treatment Using a Novel Dedicated Paediatric Brain Applicator. Cancers. 2019; 11(8):1183. https://doi.org/10.3390/cancers11081183
Chicago/Turabian StyleSchooneveldt, Gerben, Hana Dobšíček Trefná, Mikael Persson, Theo M. de Reijke, Klas Blomgren, H. Petra Kok, and Hans Crezee. 2019. "Hyperthermia Treatment Planning Including Convective Flow in Cerebrospinal Fluid for Brain Tumour Hyperthermia Treatment Using a Novel Dedicated Paediatric Brain Applicator" Cancers 11, no. 8: 1183. https://doi.org/10.3390/cancers11081183
APA StyleSchooneveldt, G., Dobšíček Trefná, H., Persson, M., de Reijke, T. M., Blomgren, K., Kok, H. P., & Crezee, H. (2019). Hyperthermia Treatment Planning Including Convective Flow in Cerebrospinal Fluid for Brain Tumour Hyperthermia Treatment Using a Novel Dedicated Paediatric Brain Applicator. Cancers, 11(8), 1183. https://doi.org/10.3390/cancers11081183