A Hybrid In Silico and Tumor-on-a-Chip Approach to Model Targeted Protein Behavior in 3D Microenvironments
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Lines and Culture Media
2.2. Cloning, Expression and Conjugation of DARPins and DARPin Fusions
2.3. Quantification of Receptor Density
2.4. Determination of Binding of DARPin to Cell Surface Receptors
2.5. Specific DARPin Binding to Tumor Cells in Co-Cultures
2.6. Toxicity of DARPin-Toxin Fusions
2.7. DARPin Penetration into Tumor Spheroids
2.8. Quantification of DARPin Penetration Depth in Tumor Spheroids
2.9. Fabrication of Tumor-on-a-Chip
2.10. Real-Time DARPin Penetration in the Tumor-on-a-Chip System
2.11. Quantification of Cell Death in Tumor-on-a-Chip System
2.12. Confocal Microscopy Imaging Settings
2.13. Mathematical Model of DARPins Diffusion In Vitro
- Equation (1). DARPin.
- Equation (2). Receptor.
- Equation (3). DARPin—receptor complex.
3. Results
3.1. Specificity of DARPins and Toxicity of DARPin-Toxin Fusion Proteins in 2D Model Systems
3.2. DARPin Delivery in 3D Multicellular Tumor Spheroids (MCTS)
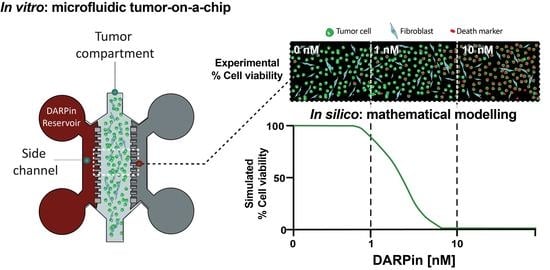
3.3. DARPin Delivery in 3D in a Microfluidic Tumor-on-a-Chip Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carter, P.J.; Lazar, G.A. Next generation antibody drugs: Pursuit of the ‘high-hanging fruit’. Nat. Rev. Drug Discov. 2018, 17, 197–223. [Google Scholar] [CrossRef]
- Jost, C.; Plückthun, A. Engineered proteins with desired specificity: DARPins, other alternative scaffolds and bispecific IgGs. Curr. Opin. Struct. Biol. 2014, 27, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Barua, S.; Mitragotri, S. Challenges associated with Penetration of Nanoparticles across Cell and Tissue Barriers: A Review of Current Status and Future Prospects. Nano Today 2014, 9, 223–243. [Google Scholar] [CrossRef] [PubMed]
- Fujimori, K.; Covell, D.G.; Fletcher, J.E.; Weinstein, J.N. Modeling Analysis of the Global and Microscopic Distribution of Immunoglobulin G, F(ab’)2, and Fab in tumors. Cancer Res. 1989, 49, 5656–5663. [Google Scholar]
- Heldin, C.H.; Rubin, K.; Pietras, K.; Ostman, A. High interstitial fluid pressure—An obstacle in cancer therapy. Nat. Rev. Cancer 2004, 4, 806–813. [Google Scholar] [CrossRef] [PubMed]
- Thurber, G.M.; Schmidt, M.M.; Wittrup, K.D. Antibody tumor penetration: Transport opposed by systemic and antigen-mediated clearance. Adv. Drug Deliv. Rev. 2008, 60, 1421–1434. [Google Scholar] [CrossRef] [Green Version]
- Torok, S.; Rezeli, M.; Kelemen, O.; Vegvari, A.; Watanabe, K.; Sugihara, Y.; Tisza, A.; Marton, T.; Kovacs, I.; Tovari, J.; et al. Limited Tumor Tissue Drug Penetration Contributes to Primary Resistance against Angiogenesis Inhibitors. Theranostics 2017, 7, 400–412. [Google Scholar] [CrossRef] [Green Version]
- Hackam, D.G.; Redelmeier, D.A. Translation of Research Evidence From Animals to Humans. JAMA 2006, 296, 1727–1732. [Google Scholar] [CrossRef]
- Rice, J. Animal models: Not close enough. Nature 2012, 484, S9. [Google Scholar] [CrossRef]
- Seok, J.; Warren, H.S.; Cuenca, A.G.; Mindrinos, M.N.; Baker, H.V.; Xu, W.; Richards, D.R.; McDonald-Smith, G.P.; Gao, H.; Hennessy, L.; et al. Genomic responses in mouse models poorly mimic human inflammatory diseases. Proc. Natl. Acad. Sci. USA 2013, 110, 3507–3512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.B. Three-dimensional tissue culture models in cancer biology. Semin. Cancer Biol. 2005, 15, 365–377. [Google Scholar] [CrossRef]
- van den Brand, D.; Massuger, L.F.; Brock, R.; Verdurmen, W.P. Mimicking Tumors: Toward More Predictive In Vitro Models for Peptide- and Protein-Conjugated Drugs. Bioconjug. Chem. 2017, 28, 846–856. [Google Scholar] [CrossRef] [Green Version]
- Friedrich, J.; Seidel, C.; Ebner, R.; Kunz-Schughart, L.A. Spheroid-based drug screen: Considerations and practical approach. Nat. Protoc. 2009, 4, 309–324. [Google Scholar] [CrossRef] [PubMed]
- Thurber, G.M.; Wittrup, K.D. Quantitative spatiotemporal analysis of antibody fragment diffusion and endocytic consumption in tumor spheroids. Cancer Res. 2008, 68, 3334–3341. [Google Scholar] [CrossRef] [Green Version]
- van Oppen, L.; Pille, J.; Stuut, C.; van Stevendaal, M.; van der Vorm, L.N.; Smeitink, J.A.M.; Koopman, W.J.H.; Willems, P.; van Hest, J.C.M.; Brock, R. Octa-arginine boosts the penetration of elastin-like polypeptide nanoparticles in 3D cancer models. Eur. J. Pharm. Biopharm. 2019, 137, 175–184. [Google Scholar] [CrossRef]
- Hjelstuen, M.H.; Rasch-Halvorsen, K.; Brekken, C.; Bruland, O.; de, L.D.C. Penetration and binding of monoclonal antibody in human osteosarcoma multicell spheroids. Comparison of confocal laser scanning microscopy and autoradiography. Acta Oncol. 1996, 35, 273–279. [Google Scholar] [CrossRef] [PubMed]
- Esch, E.W.; Bahinski, A.; Huh, D. Organs-on-chips at the frontiers of drug discovery. Nat. Rev. Drug Discov. 2015, 14, 248–260. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Portillo-Lara, R.; Annabi, N. Microengineered cancer-on-a-chip platforms to study the metastatic microenvironment. Lab Chip 2016, 16, 4063–4081. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.S.; Zhang, Y.-N.; Zhang, W. Cancer-on-a-chip systems at the frontier of nanomedicine. Drug Discov. Today 2017, 22, 1392–1399. [Google Scholar] [CrossRef]
- Chernyavska, M.; Schmid, M.; Freitag, P.C.; Palacio-Castaneda, V.; Piruska, A.; Huck, W.T.S.; Pluckthun, A.; Verdurmen, W.P.R. Unravelling Receptor and RGD Motif Dependence of Retargeted Adenoviral Vectors using Advanced Tumor Model Systems. Sci. Rep. 2019, 9, 18568. [Google Scholar] [CrossRef]
- Nguyen, M.; De Ninno, A.; Mencattini, A.; Mermet-Meillon, F.; Fornabaio, G.; Evans, S.S.; Cossutta, M.; Khira, Y.; Han, W.; Sirven, P.; et al. Dissecting Effects of Anti-cancer Drugs and Cancer-Associated Fibroblasts by On-Chip Reconstitution of Immunocompetent Tumor Microenvironments. Cell Rep. 2018, 25, 3884–3893.e3883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sung, K.E.; Beebe, D.J. Microfluidic 3D models of cancer. Adv. Drug Deliv. Rev. 2014, 79–80, 68–78. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palacio-Castañeda, V.; Kooijman, L.; Venzac, B.; Verdurmen, W.P.R.; Le Gac, S. Metabolic Switching of Tumor Cells under Hypoxic Conditions in a Tumor-on-a-chip Model. Micromachines 2020, 11, 382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cilliers, C.; Guo, H.; Liao, J.; Christodolu, N.; Thurber, G.M. Multiscale Modeling of Antibody-Drug Conjugates: Connecting Tissue and Cellular Distribution to Whole Animal Pharmacokinetics and Potential Implications for Efficacy. AAPS J. 2016, 18, 1117–1130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Boer, E.; Warram, J.M.; Tucker, M.D.; Hartman, Y.E.; Moore, L.S.; de Jong, J.S.; Chung, T.K.; Korb, M.L.; Zinn, K.R.; van Dam, G.M.; et al. In Vivo Fluorescence Immunohistochemistry: Localization of Fluorescently Labeled Cetuximab in Squamous Cell Carcinomas. Sci. Rep. 2015, 5, 10169. [Google Scholar] [CrossRef] [Green Version]
- Juweid, M.; Neumann, R.; Paik, C.; Perez-Bacete, M.J.; Sato, J.; van Osdol, W.; Weinstein, J.N. Micropharmacology of monoclonal antibodies in solid tumors: Direct experimental evidence for a binding site barrier. Cancer Res. 1992, 52, 5144–5153. [Google Scholar]
- d’Esposito, A.; Sweeney, P.W.; Ali, M.; Saleh, M.; Ramasawmy, R.; Roberts, T.A.; Agliardi, G.; Desjardins, A.; Lythgoe, M.F.; Pedley, R.B.; et al. Computational fluid dynamics with imaging of cleared tissue and of in vivo perfusion predicts drug uptake and treatment responses in tumours. Nat. Biomed. Eng. 2018, 2, 773–787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torres, C.; Dumas, S.; Palacio-Castañeda, V.; Descroix, S.; Brock, R.; Verdurmen, W.P.R. A Computational Investigation of In Vivo Cytosolic Protein Delivery for Cancer Therapy. Pharmaceutics 2021, 13, 562. [Google Scholar] [CrossRef]
- Binz, H.K.; Amstutz, P.; Kohl, A.; Stumpp, M.T.; Briand, C.; Forrer, P.; Grutter, M.G.; Pluckthun, A. High-affinity binders selected from designed ankyrin repeat protein libraries. Nat. Biotechnol. 2004, 22, 575–582. [Google Scholar] [CrossRef]
- Zahnd, C.; Kawe, M.; Stumpp, M.T.; de Pasquale, C.; Tamaskovic, R.; Nagy-Davidescu, G.; Dreier, B.; Schibli, R.; Binz, H.K.; Waibel, R.; et al. Efficient tumor targeting with high-affinity designed ankyrin repeat proteins: Effects of affinity and molecular size. Cancer Res. 2010, 70, 1595–1605. [Google Scholar] [CrossRef] [Green Version]
- Distelmaier, F.; Valsecchi, F.; Forkink, M.; van Emst-de Vries, S.; Swarts, H.G.; Rodenburg, R.J.T.; Verwiel, E.T.P.; Smeitink, J.A.M.; Willems, P.H.G.M.; Koopman, W.J.H. Trolox-Sensitive Reactive Oxygen Species Regulate Mitochondrial Morphology, Oxidative Phosphorylation and Cytosolic Calcium Handling in Healthy Cells. Antioxid. Redox Signal. 2012, 17, 1657–1669. [Google Scholar] [CrossRef] [PubMed]
- van den Brand, D.; van Lith, S.A.M.; de Jong, J.M.; Gorris, M.A.J.; Palacio-Castaneda, V.; Couwenbergh, S.T.; Goldman, M.R.G.; Ebisch, I.; Massuger, L.F.; Leenders, W.P.J.; et al. EpCAM-Binding DARPins for Targeted Photodynamic Therapy of Ovarian Cancer. Cancers 2020, 12, 1762. [Google Scholar] [CrossRef] [PubMed]
- Verdurmen, W.P.; Luginbühl, M.; Honegger, A.; Plückthun, A. Efficient cell-specific uptake of binding proteins into the cytoplasm through engineered modular transport systems. J. Control. Release 2015, 200, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [Green Version]
- Steiner, D.; Forrer, P.; Pluckthun, A. Efficient selection of DARPins with sub-nanomolar affinities using SRP phage display. J. Mol. Biol. 2008, 382, 1211–1227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stefan, N.; Martin-Killias, P.; Wyss-Stoeckle, S.; Honegger, A.; Zangemeister-Wittke, U.; Pluckthun, A. DARPins recognizing the tumor-associated antigen EpCAM selected by phage and ribosome display and engineered for multivalency. J. Mol. Biol. 2011, 413, 826–843. [Google Scholar] [CrossRef] [PubMed]
- Hendriks, B.S.; Opresko, L.K.; Wiley, H.S.; Lauffenburger, D. Quantitative analysis of HER2-mediated effects on HER2 and epidermal growth factor receptor endocytosis: Distribution of homo- and heterodimers depends on relative HER2 levels. J. Biol. Chem. 2003, 278, 23343–23351. [Google Scholar] [CrossRef] [Green Version]
- Hazin, J.; Moldenhauer, G.; Altevogt, P.; Brady, N.R. A novel method for measuring cellular antibody uptake using imaging flow cytometry reveals distinct uptake rates for two different monoclonal antibodies targeting L1. J. Immunol. Methods 2015, 423, 70–77. [Google Scholar] [CrossRef]
- Martin-Killias, P.; Stefan, N.; Rothschild, S.; Pluckthun, A.; Zangemeister-Wittke, U. A novel fusion toxin derived from an EpCAM-specific designed ankyrin repeat protein has potent antitumor activity. Clin. Cancer Res. 2011, 17, 100–110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hathaway, H.J.; Butler, K.S.; Adolphi, N.L.; Lovato, D.M.; Belfon, R.; Fegan, D.; Monson, T.C.; Trujillo, J.E.; Tessier, T.E.; Bryant, H.C.; et al. Detection of breast cancer cells using targeted magnetic nanoparticles and ultra-sensitive magnetic field sensors. Breast Cancer Res. 2011, 13, R108. [Google Scholar] [CrossRef] [Green Version]
- Kreft, M.E.; Jerman, U.D.; Lasic, E.; Hevir-Kene, N.; Rizner, T.L.; Peternel, L.; Kristan, K. The characterization of the human cell line Calu-3 under different culture conditions and its use as an optimized in vitro model to investigate bronchial epithelial function. Eur. J. Pharm. Sci. 2015, 69, 1–9. [Google Scholar] [CrossRef]
- Bunn, P.A., Jr.; Helfrich, B.; Soriano, A.F.; Franklin, W.A.; Varella-Garcia, M.; Hirsch, F.R.; Baron, A.; Zeng, C.; Chan, D.C. Expression of Her-2/neu in human lung cancer cell lines by immunohistochemistry and fluorescence in situ hybridization and its relationship to in vitro cytotoxicity by trastuzumab and chemotherapeutic agents. Clin. Cancer Res. 2001, 7, 3239–3250. [Google Scholar] [PubMed]
- Bartelink, I.H.; Jones, E.F.; Shahidi-Latham, S.K.; Lee, P.R.E.; Zheng, Y.; Vicini, P.; van’t Veer, L.; Wolf, D.; Iagaru, A.; Kroetz, D.L.; et al. Tumor Drug Penetration Measurements Could Be the Neglected Piece of the Personalized Cancer Treatment Puzzle. Clin. Pharmacol. Ther. 2019, 106, 148–163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dogra, P.; Butner, J.D.; Chuang, Y.L.; Caserta, S.; Goel, S.; Brinker, C.J.; Cristini, V.; Wang, Z. Mathematical modeling in cancer nanomedicine: A review. Biomed. Microdevices 2019, 21, 40. [Google Scholar] [CrossRef] [Green Version]
- Mircioiu, C.; Voicu, V.; Anuta, V.; Tudose, A.; Celia, C.; Paolino, D.; Fresta, M.; Sandulovici, R.; Mircioiu, I. Mathematical Modeling of Release Kinetics from Supramolecular Drug Delivery Systems. Pharmaceutics 2019, 11, 140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agoram, B.M. Use of pharmacokinetic/ pharmacodynamic modelling for starting dose selection in first-in-human trials of high-risk biologics. Br. J. Clin. Pharmacol. 2009, 67, 153–160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Y.; Cao, Y. Modeling the dynamics of antibody-target binding in living tumors. Sci. Rep. 2020, 10, 16764. [Google Scholar] [CrossRef]
- Saga, T.; Neumann, R.D.; Heya, T.; Sato, J.; Kinuya, S.; Le, N.; Paik, C.H.; Weinstein, J.N. Targeting cancer micrometastases with monoclonal antibodies: A binding-site barrier. Proc. Natl. Acad. Sci. USA 1995, 92, 8999–9003. [Google Scholar] [CrossRef] [Green Version]
- Debie, P.; Lafont, C.; Defrise, M.; Hansen, I.; van Willigen, D.M.; van Leeuwen, F.W.B.; Gijsbers, R.; D’Huyvetter, M.; Devoogdt, N.; Lahoutte, T.; et al. Size and affinity kinetics of nanobodies influence targeting and penetration of solid tumours. J. Control. Release 2020, 317, 34–42. [Google Scholar] [CrossRef]
- Xenaki, K.T.; Oliveira, S.; van Bergen En Henegouwen, P.M.P. Antibody or Antibody Fragments: Implications for Molecular Imaging and Targeted Therapy of Solid Tumors. Front. Immunol. 2017, 8, 1287. [Google Scholar] [CrossRef]
- Ramanujan, S.; Pluen, A.; McKee, T.D.; Brown, E.B.; Boucher, Y.; Jain, R.K. Diffusion and convection in collagen gels: Implications for transport in the tumor interstitium. Biophys. J. 2002, 83, 1650–1660. [Google Scholar] [CrossRef] [Green Version]
- Hughes, C.S.; Postovit, L.M.; Lajoie, G.A. Matrigel: A complex protein mixture required for optimal growth of cell culture. Proteomics 2010, 10, 1886–1890. [Google Scholar] [CrossRef] [PubMed]
- Weniger, M.; Honselmann, K.C.; Liss, A.S. The Extracellular Matrix and Pancreatic Cancer: A Complex Relationship. Cancers 2018, 10, 316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holzinger, A. From Machine Learning to Explainable AI. In Proceedings of the 2018 World Symposium on Digital Intelligence for Systems and Machines (DISA), Košice, Slovakia, 23–25 August 2018; pp. 55–66. [Google Scholar]
- Budge, E.J.; Tsoti, S.M.; Howgate, D.J.; Sivakumar, S.; Jalali, M. Collective intelligence for translational medicine: Crowdsourcing insights and innovation from an interdisciplinary biomedical research community. Ann. Med. 2015, 47, 570–575. [Google Scholar] [CrossRef] [Green Version]





| Parameter | Value and Units | Reference |
|---|---|---|
| Void fraction tumor-on-a-chip (ε) | 0.80 | Experimental a |
| Void fraction spheroids (ε) | 0.15 | [14] |
| Re0 tumor-on-a-chip (BT-474) | HER2: 2.18 nm EpCAM: 2.45 nm | Calculated b |
| Re0 spheroids (BT-474) | HER2: 234 nm EpCAM: 263 nm | Calculated d |
| kon | HER2-binding DARPin 9_26: 7.38 × 104 m−1·s−1 EpCAM-binding DARPin Ec1: 3.65 × 105 m−1·s−1 | [35,36] |
| koff | HER2-binding DARPin 9_26: 0.1 × 10−3 s−1 EpCAM-binding DARPin Ec1: 3.65 × 105 s−1 | [35,36] |
| ke | HER2: 1.67 × 10−4 s−1 EpCAM: 3.46 × 10−5 s−1 | [37,38] |
| Diffusion coefficient DWater (DARPin) | 164 µm2·s−1 | Estimated c |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palacio-Castañeda, V.; Dumas, S.; Albrecht, P.; Wijgers, T.J.; Descroix, S.; Verdurmen, W.P.R. A Hybrid In Silico and Tumor-on-a-Chip Approach to Model Targeted Protein Behavior in 3D Microenvironments. Cancers 2021, 13, 2461. https://doi.org/10.3390/cancers13102461
Palacio-Castañeda V, Dumas S, Albrecht P, Wijgers TJ, Descroix S, Verdurmen WPR. A Hybrid In Silico and Tumor-on-a-Chip Approach to Model Targeted Protein Behavior in 3D Microenvironments. Cancers. 2021; 13(10):2461. https://doi.org/10.3390/cancers13102461
Chicago/Turabian StylePalacio-Castañeda, Valentina, Simon Dumas, Philipp Albrecht, Thijmen J. Wijgers, Stéphanie Descroix, and Wouter P. R. Verdurmen. 2021. "A Hybrid In Silico and Tumor-on-a-Chip Approach to Model Targeted Protein Behavior in 3D Microenvironments" Cancers 13, no. 10: 2461. https://doi.org/10.3390/cancers13102461
APA StylePalacio-Castañeda, V., Dumas, S., Albrecht, P., Wijgers, T. J., Descroix, S., & Verdurmen, W. P. R. (2021). A Hybrid In Silico and Tumor-on-a-Chip Approach to Model Targeted Protein Behavior in 3D Microenvironments. Cancers, 13(10), 2461. https://doi.org/10.3390/cancers13102461