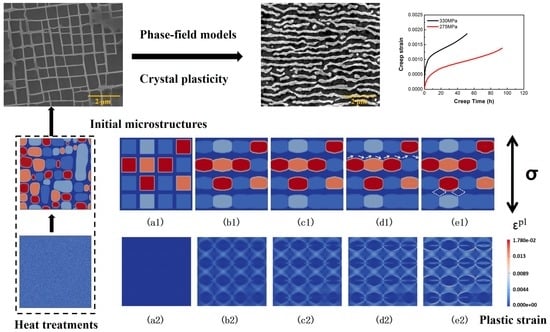
Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation
Abstract
:1. Introduction
2. γ’ Rafting Behavior in Superalloys
2.1. Types of Rafting
2.2. Kinetics of Rafting
3. Crystal Plasticity Models
3.1. Crystal Plasticity Theory
3.2. Phenomenological Constitutive Models
3.3. Physics-Based Constitutive Models
4. Phase-Field Models
4.1. Phase-Field Method
4.2. Ni-Al Binary System
4.3. Multiphase-Field Model
5. Application of Crystal Plasticity and Phase-Field Method in the Rafting Analysis
5.1. Uniaxial Tension
5.2. Creep Deformation
5.2.1. N-Type/P-Type Rafting
5.2.2. Complex Types of Rafting
5.2.3. Collapse and Topological Inversion
6. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Murakumo, T.; Kobayashi, T.; Koizumi, Y.; Harada, H. Creep behaviour of Ni-base single-crystal superalloys with various γ’ volume fraction. Acta Mater. 2004, 52, 3737–3744. [Google Scholar] [CrossRef]
- Yue, Q.; Liu, L.; Yang, W.; He, C.; Sun, D.; Huang, T.; Zhang, J.; Fu, H. Stress dependence of the creep behaviors and mechanisms of a third-generation Ni-based single crystal superalloy. J. Mater. Sci. Technol. 2019, 35, 752–763. [Google Scholar] [CrossRef]
- Xia, W.; Zhao, X.; Yue, L.; Zhang, Z. A review of composition evolution in Ni-based single crystal superalloys. J. Mater. Sci. Technol. 2020, 44, 76–95. [Google Scholar] [CrossRef]
- Pearson, D.; Lemkey, F.; Kear, B. Stress Coarsening of γ’ and its Influence on Creep Properties of a Single Crystal Superalloy. In Proceedings of the 4th International Symposium on Superallos, Champion, PA, USA, 21–25 September 1980; pp. 513–520. [Google Scholar]
- Henderson, P.J.; Mclean, M. Microstructural contributions to friction stress and recovery kinetics during creep of the nickel-base superalloy IN738LC. Acta Metall. 1983, 31, 1203–1219. [Google Scholar] [CrossRef]
- Pollock, T.M.; Argon, A.S. Directional coarsening in nickel-base single crystals with high volume fractions of coherent precipitates. Acta Metall. Mater. 1994, 42, 1859–1874. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, W.; Wen, Z.; Tong, W.; Zhang, Y.; Yue, Z.; He, P. Creep residual life prediction of a nickel-based single crystal superalloy based on microstructure evolution. Mater. Sci. Eng. A 2019, 756, 108–118. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, X.; Yue, Z.; Sun, S. Visco-plasticity phase-field simulation of the mechanical property and rafting behavior in nickel-based superalloys. Intermetallics 2020, 125, 106884. [Google Scholar] [CrossRef]
- Epishin, A.; Link, T.; Portella, P.D.; Bruckner, U. Evolution of the γ/γ’ microstructure during high-temperature creep of a nickel-base superalloy. Acta Mater. 2000, 48, 4169–4177. [Google Scholar] [CrossRef]
- Wu, W.P.; Li, S.Y.; Li, Y.L. An anisotropic elastic–plastic model for predicting the rafting behavior in Ni-based single crystal superalloys. Mech. Mater. 2019, 132, 9–17. [Google Scholar] [CrossRef]
- Fratzl, P.; Paris, O. Strain-induced morphologies during homogeneous phase separation in alloys. Phase Transit. 1999, 67, 707–724. [Google Scholar] [CrossRef]
- Gaubert, A.; le Bouar, Y.; Finel, A. Coupling phase field and viscoplasticity to study rafting in Ni-based superalloys. Philos. Mag. 2010, 90, 375–404. [Google Scholar] [CrossRef]
- Boussinot, G.; le Bouar, Y.; Finel, A. Phase-field simulations with inhomogeneous elasticity: Comparison with an atomic-scale method and application to superalloys. Acta Mater. 2010, 58, 4170–4181. [Google Scholar] [CrossRef]
- Kundin, J.; Mushongera, L.; Goehler, T.; Emmerich, H. Phase-field modeling of the γ’-coarsening behavior in Ni-based superalloys. Acta Mater. 2012, 60, 3758–3772. [Google Scholar] [CrossRef]
- Cottura, M.; le Bouar, Y.; Appolaire, B.; Finel, A. Rôle of elastic inhomogeneity in the development of cuboidal microstructures in Ni-based superalloys. Acta Mater. 2015, 94, 15–25. [Google Scholar] [CrossRef]
- Zhou, N.; Shen, C.; Mills, M.; Wang, Y.Z. Large-scale three-dimensional phase field simulation of γ’-rafting and creep deformation. Philos. Mag. 2010, 90, 405–436. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, L.; Tong, J. Discrete dislocation dynamics modelling of mechanical deformation of nickel-based single crystal superalloys. Int. J. Plast. 2012, 28, 141–158. [Google Scholar] [CrossRef] [Green Version]
- Wu, R.; Zaiser, M.; Sandfeld, S. A continuum approach to combined γ/γ’ evolution and dislocation plasticity in Nickel-based superalloys. Int. J. Plast. 2017, 95, 142–162. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, J.; Wei, H.; Gui, W.M.; Su, H.J.; Jin, T.; Liu, L. A phase-field model for creep behavior in nickel-base single-crystal superalloy: Coupled with creep damage. Scr. Mater. 2018, 147, 16–20. [Google Scholar] [CrossRef]
- Tsukada, Y.; Koyama, T.; Kubota, F.; Murata, Y.; Kondo, Y. Phase-field simulation of rafting kinetics in a nickel-based single crystal superalloy. Intermetallics 2017, 85, 187–196. [Google Scholar] [CrossRef]
- Jokisaari, A.M.; Naghavi, S.S.; Wolverton, C.; Voorhees, P.W.; Heinonen, O.G. Predicting the morphologies of γʹ precipitates in cobalt-based superalloys. Acta Mater. 2017, 141, 273–284. [Google Scholar] [CrossRef]
- Wang, C.; Ali, M.A.; Gao, S.; Goerler, J.V.; Steinbach, I. Combined phase-field crystal plasticity simulation of P- and N-type rafting in Co-based superalloys. Acta Mater. 2019, 175, 21–34. [Google Scholar] [CrossRef]
- Tsao, T.K.; Yeh, A.C.; Kuo, C.M.; Kakehi, K.; Murakami, H.; Yeh, J.W.; Jian, S.R. The High Temperature Tensile and Creep Behaviors of High Entropy Superalloy. Sci. Rep. 2017, 7, 12658. [Google Scholar] [CrossRef] [PubMed]
- Sauza, D.J.; Dunand, D.C.; Seidman, D.N. Microstructural evolution and high-temperature strength of a γ(fcc)/γ’(L12) Co–Al–W–Ti–B superalloy. Acta Mater. 2019, 174, 427–438. [Google Scholar] [CrossRef]
- Schmidt, I.; Gross, D. Directional coarsening in Ni–base superalloys: Analytical results for an elasticity–based model. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 455, 3085–3106. [Google Scholar] [CrossRef]
- Gururajan, M.P.; Abinandanan, T.A. Phase field study of precipitate rafting under a uniaxial stress. Acta Mater. 2007, 55, 5015–5026. [Google Scholar] [CrossRef]
- Ott, M.; Mughrabi, H. Dependence of the high-temperature low-cycle fatigue behaviour of the monocrystalline nickel-base superalloys CMSX-4 and CMSX-6 on the γ/γ’-morphology. Mater. Sci. Eng. A 1999, 272, 24–30. [Google Scholar] [CrossRef]
- Mughrabi, H.; Tetzlaff, U. Microstructure and High-Temperature Strength of Monocrystalline Nickel-Base Superalloys. Adv. Eng. Mater. 2000, 2, 319–326. [Google Scholar] [CrossRef]
- Shui, L.; Jin, T.; Tian, S.; Hu, Z. Influence of precipitate morphology on tensile creep of a single crystal nickel-base superalloy. Mater. Sci. Eng. A 2007, 454, 461–466. [Google Scholar] [CrossRef]
- Tian, S.G.; Wang, M.G.; Yu, H.C.; Yu, X.F.; Li, T.; Qian, B.J. Influence of element Re on lattice misfits and stress rupture properties of single crystal nickel-based superalloys. Mater. Sci. Eng. A 2010, 527, 4458–4465. [Google Scholar]
- Mughrabi, H. The importance of sign and magnitude of γ/γ’ lattice misfit in superalloys—With special reference to the new γ’-hardened cobalt-base superalloys. Acta Mater. 2014, 81, 21–29. [Google Scholar] [CrossRef]
- Yu, J.; Sun, Y.; Sun, X.; Jin, T.; Hu, Z. Anisotropy of high cycle fatigue behavior of a Ni-base single crystal superalloy. Mater. Sci. Eng. A 2013, 566, 90–95. [Google Scholar] [CrossRef]
- Wen, Z.; Zhang, D.; Li, S.; Yue, Z.; Gao, J. Anisotropic creep damage and fracture mechanism of nickel-base single crystal superalloy under multiaxial stress. J. Alloys Compd. 2017, 692, 301–312. [Google Scholar] [CrossRef]
- Fan, Y.N.; Shi, H.J.; Qiu, W.H. Constitutive modeling of creep behavior in single crystal superalloys: Effects of rafting at high temperatures. Mater. Sci. Eng. A 2015, 644, 225–233. [Google Scholar] [CrossRef]
- Han, G.M.; Yu, J.J.; Hu, Z.Q.; Sun, X.F. Creep property and microstructure evolution of a nickel-base single crystal superalloy in orientation. Mater. Charact. 2013, 86, 177–184. [Google Scholar] [CrossRef]
- Yu, H.C.; Su, Y.; Tian, N.; Tian, S.G.; Li, Y.; Yu, X.F.; Yu, L.L. Microstructure evolution and creep behavior of a oriented single crystal nickel-based superalloy during tensile creep. Mater. Sci. Eng. A 2013, 565, 292–300. [Google Scholar] [CrossRef]
- Chatterjee, D.; Hazari, N.; Das, N.; Mitra, R. Microstructure and creep behavior of DMS4-type nickel based superalloy single crystals with orientations near <001> and <011>. Mater. Sci. Eng. A 2010, 528, 604–613. [Google Scholar] [CrossRef]
- Tian, S.; Su, Y.; Yu, L.; Yu, H.; Zhang, S.; Qian, B. Microstructure evolution of a orientation single crystal nickel-base superalloy during tensile creep. Appl. Phys. A 2011, 104, 643–647. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Zhang, G.; Zheng, W.; Qi, D.; Du, K.; Zhang, J.; Lou, L. Creep deformation related to γ’ phase cutting at high temperature of a oriented nickel-base single crystal superalloy. Mater. Sci. Eng. A 2019, 763, 138162. [Google Scholar] [CrossRef]
- Kamaraj, M. Rafting in single crystal nickel-base superalloys—An overview. Sadhana 2003, 28, 115–128. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Yang, C.; Xu, Q.Y. Numerical simulation of microstructure evolution in Ni-based superalloys during P-type rafting using multiphase-field model and crystal plasticity. Comput. Mater. Sci. 2020, 172, 109331. [Google Scholar] [CrossRef]
- Mushongera, L.T.; Fleck, M.; Kundin, J.; Wang, Y.; Emmerich, H. Effect of Re on directional γ’-coarsening in commercial single crystal Ni-base superalloys: A phase field study. Acta Mater. 2015, 93, 60–72. [Google Scholar] [CrossRef]
- Tian, S.G.; Zhang, S.; Liang, F.S.; Li, A.A.; Li, J.J. Microstructure evolution and analysis of a single crystal nickel-based superalloy during compressive creep. Mater. Sci. Eng. A 2011, 528, 4988–4993. [Google Scholar] [CrossRef]
- Fedelich, B.; Künecke, G.; Epishin, A.; Link, T.; Portella, P. Constitutive modelling of creep degradation due to rafting in single-crystalline Ni-base superalloys. Mater. Sci. Eng. A 2009, 510, 273–277. [Google Scholar] [CrossRef]
- Tinga, T.; Brekelmans, W.; Geers, M. Directional coarsening in nickel-base superalloys and its effect on the mechanical properties. Comput. Mater. Sci. 2009, 47, 471–481. [Google Scholar] [CrossRef]
- Caron, P.; Ramusat, C.; Diologent, F. Influence of the γ’ fraction on the γ/γ’ topological inversion during high temperature creep of single crystal superalloys. In Proceedings of the 11th International Symposium on Superalloys: SUPERALLOYS 2008, Seven Springs, PA, USA, 14–18 September 2008; pp. 159–167. [Google Scholar]
- Bergonnier, S.; Hild, F.; Roux, S. Local anisotropy analysis for non-smooth images. Pattern Recognit. 2007, 40, 544–556. [Google Scholar] [CrossRef] [Green Version]
- Caccuri, V.; Desmorat, R.; Cormier, J. Tensorial nature of γ’-rafting evolution in nickel-based single crystal superalloys. Acta Mater. 2018, 158, 138–154. [Google Scholar] [CrossRef]
- Nguyen, L.; Shi, R.P.; Wang, Y.Z.; de Graef, M. Quantification of rafting of γ’ precipitates in Ni-based superalloys. Acta Mater. 2016, 103, 322–333. [Google Scholar] [CrossRef] [Green Version]
- Desmorat, R.; Mattiello, A.; Cormier, J. A tensorial thermodynamic framework to account for the γ’ rafting in nickel-based single crystal superalloys. Int. J. Plast. 2017, 95, 43–81. [Google Scholar] [CrossRef] [Green Version]
- Tinga, T.; Brekelmans, W.A.M.; Geers, M.G.D. Incorporating strain gradient effects in a multiscale constitutive framework for nickel-base superalloys. Philos. Mag. 2008, 88, 3793–3825. [Google Scholar] [CrossRef]
- Henderson, P.; Berglin, L.; Jansson, C. On rafting in a single crystal nickel-base superalloy after high and low temperature creep. Scr. Mater. 1998, 40, 229–234. [Google Scholar] [CrossRef]
- Matan, N.; Cox, D.; Rae, C.; Reed, R. On the kinetics of rafting in CMSX-4 superalloy single crystals. Acta Mater. 1999, 47, 2031–2045. [Google Scholar] [CrossRef]
- Taylor, C.F.E.G.I. The Distortion of an Aluminum Crystal during a Tensile Test. Proc. R. Soc. 1923, 102, 634–667. [Google Scholar]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Chowdhury, H.; Naumenko, K.; Altenbach, H. Aspects of power law flow rules in crystal plasticity with glide-climb driven hardening and recovery. Int. J. Mech. Sci. 2018, 146, 486–496. [Google Scholar] [CrossRef]
- Frost, H.J.; Ashby, M.F. Deformation Mechanism Maps: The Plasticity and Creep of Metals and Ceramics; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Kamaraj, M.; Radhakrishnan, V. First Report on the Deformation Mechanism Mapping of First and Second Generation Ni-Based Single Crystal Super Alloys. Trans. Indian Inst. Metals 2017, 70, 2485–2496. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Bassani, J.L.; Wu, T.Y. Latent hardening in single crystals. II. Analytical characterization and predictions. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 435, 21–41. [Google Scholar]
- Wang, X.M.; Hui, Y.Z.; Hou, Y.Y.; Yu, Z.Y.; Li, L.; Yue, Z.F.; Deng, C.H. Direct investigation on high temperature tensile and creep behavior at different regions of directional solidified cast turbine blades. Mech. Mater. 2019, 136, 103068. [Google Scholar] [CrossRef]
- Me’ric, L.; Poubanne, P.; Cailletaud, G. Single crystal modeling for structural calculations: Part 1—Model presentation. J. Eng. Mater. Technol. 1991, 113, 162–170. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Flewitt, P.; Smith, D.; Cocks, A.; Zhang, S. Quantifying internal stress and internal resistance associated with thermal ageing and creep in a polycrystalline material. Acta Mater. 2014, 67, 207–219. [Google Scholar] [CrossRef]
- Hoppe, R.; Appel, F. Origin and magnitude of internal stresses in TiAl alloys. In Gamma Titanium Aluminide Alloys 2014: A Collection of Research on Innovation and Commercialization of Gamma Alloy Technology; Wiley: Hoboken, NJ, USA, 2014; pp. 159–168. [Google Scholar]
- Kumar, A.V.; Yang, C. Study of work hardening models for single crystals using three dimensional finite element analysis. Int. J. Plast. 1999, 15, 737–754. [Google Scholar] [CrossRef]
- Cottura, M.; Appolaire, B.; Finel, A.; le Bouar, Y. Coupling the Phase Field Method for diffusive transformations with dislocation density-based crystal plasticity: Application to Ni-based superalloys. J. Mech. Phys. Solids 2016, 94, 473–489. [Google Scholar] [CrossRef]
- Arsenlis, A.; Parks, D.M.; Becker, R.; Bulatov, V.V. On the evolution of crystallographic dislocation density in non-homogeneously deforming crystals. J. Mech. Phys. Solids 2004, 52, 1213–1246. [Google Scholar] [CrossRef]
- Arsenlis, A.; Parks, D.M. Modeling the evolution of crystallographic dislocation density in crystal plasticity. J. Mech. Phys. Solids 2002, 50, 1979–2009. [Google Scholar] [CrossRef]
- Ma, A.; Roters, F.; Raabe, D. On the consideration of interactions between dislocations and grain boundaries in crystal plasticity finite element modeling—Theory, experiments, and simulations. Acta Mater. 2006, 54, 2181–2194. [Google Scholar] [CrossRef]
- Ma, A.; Roters, F.; Raabe, D. A dislocation density based constitutive model for crystal plasticity FEM including geometrically necessary dislocations. Acta Mater. 2006, 54, 2169–2179. [Google Scholar] [CrossRef]
- Fleck, N.; Muller, G.; Ashby, M.F.; Hutchinson, J.W. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Evers, L.; Brekelmans, W.; Geers, M. Non-local crystal plasticity model with intrinsic SSD and GND effects. J. Mech. Phys. Solids 2004, 52, 2379–2401. [Google Scholar] [CrossRef]
- Devincre, B.; Kubin, L.; Hoc, T. Physical analyses of crystal plasticity by DD simulations. Scr. Mater. 2006, 54, 741–746. [Google Scholar] [CrossRef]
- Chaboche, J.L. A review of some plasticity and viscoplasticity constitutive theories. Int. J. Plast. 2008, 24, 1642–1693. [Google Scholar] [CrossRef]
- Van der Waals, J.D. Thermodynamische Theorie der Kapillaritat unter voraussetzung stetiger Dichteanderung. Z. Phys. Chem. 1894, 13, 657–725. [Google Scholar]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. An introduction to phase-field modeling of microstructure evolution. Calphad 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Wang, Y.; Banerjee, D.; Su, C.; Khachaturyan, A. Field kinetic model and computer simulation of precipitation of L12 ordered intermetallics from fcc solid solution. Acta Mater. 1998, 46, 2983–3001. [Google Scholar] [CrossRef]
- Harikrishnan, R.; le Graverend, J.B. A creep-damage phase-field model: Predicting topological inversion in Ni-based single crystal superalloys. Mater. Des. 2018, 160, 405–416. [Google Scholar] [CrossRef]
- Amin, W.; Ali, M.A.; Vajragupta, N.; Hartmaier, A. Studying grain boundary strengthening by dislocation-based strain gradient crystal plasticity coupled with a multi-phase-field model. Materials 2019, 12, 2977. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.C.; Osawa, M.; Yokokawa, T.; Harada, H.; Enomoto, M. Modeling the microstructural evolution of Ni-base superalloys by phase field method combined with CALPHAD and CVM. Comput. Mater. Sci. 2007, 39, 871–879. [Google Scholar] [CrossRef]
- Wang, S.L.; Sekerka, R.; Wheeler, A.; Murray, B.; Coriell, S.; Braun, R.; McFadden, G. Thermodynamically-consistent phase-field models for solidification. Phys. D Nonlinear Phenom. 1993, 69, 189–200. [Google Scholar] [CrossRef]
- Tsukada, Y.; Murata, Y.; Koyama, T.; Morinaga, M. Phase-field simulation on the formation and collapse processes of the rafted structure in Ni-based superalloys. Mater. Trans. 2008, 49, 484–488. [Google Scholar] [CrossRef] [Green Version]
- Schleifer, F.; Holzinger, M.; Lin, Y.Y.; Glatzel, U.; Fleck, M. Phase-field modeling of γ/γ″ microstructure formation in Ni-based superalloys with high γ″ volume fraction. Intermetallics 2020, 120, 106745. [Google Scholar] [CrossRef] [Green Version]
- Gurtin, M.E. A gradient theory of single-crystal viscoplasticity that accounts for geometrically necessary dislocations. J. Mech. Phys. Solids 2002, 50, 5–32. [Google Scholar] [CrossRef]
- Steinbach, I.; Apel, M. Multi phase field model for solid state transformation with elastic strain. Phys. D Nonlinear Phenom. 2006, 217, 153–160. [Google Scholar] [CrossRef]
- Cottura, M.; le Bouar, Y.; Finel, A.; Appolaire, B.; Ammar, K.; Forest, S. A phase field model incorporating strain gradient viscoplasticity: Application to rafting in Ni-base superalloys. J. Mech. Phys. Solids 2012, 60, 1243–1256. [Google Scholar] [CrossRef]
- Zhou, N.; Shen, C.; Mills, M.J.; Wang, Y. Contributions from elastic inhomogeneity and from plasticity to γ’ rafting in single-crystal Ni–Al. Acta Mater. 2008, 56, 6156–6173. [Google Scholar] [CrossRef]
- Touratier, F.; Andrieu, E.; Poquillon, D.; Viguier, B. Rafting microstructure during creep of the MC2 nickel-based superalloy at very high temperature. Mater. Sci. Eng. A 2009, 510, 244–249. [Google Scholar] [CrossRef] [Green Version]
- Gaubert, A.; Jouiad, M.; Cormier, J.; le Bouar, Y.; Ghighi, J. Three-dimensional imaging and phase-field simulations of the microstructure evolution during creep tests of <011>-oriented Ni-based superalloys. Acta Mater. 2015, 84, 237–255. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, J.; Wei, H.; Zhao, Y.; Gui, W.; Su, H.; Jin, T.; Liu, L. Study of γ’ rafting under different stress states—A phase-field simulation considering viscoplasticity. J. Alloy. Compd. 2018, 769, 453–462. [Google Scholar] [CrossRef]
- Ali, M.A.; Amin, W.; Shchyglo, O.; Steinbach, I. 45-degree rafting in Ni-based superalloys: A combined phase-field and strain gradient crystal plasticity study. Int. J. Plast. 2020, 128, 102659. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, X.; Yue, Z. The effect of stress state on rafting mechanism and cyclic creep behavior of Ni-base superalloy. Mech. Mater. 2020, 149, 103563. [Google Scholar] [CrossRef]
- Goerler, J.V.; Lopez-Galilea, I.; Roncery, L.M.; Shchyglo, O.; Theisen, W.; Steinbach, I. Topological phase inversion after long-term thermal exposure of nickel-base superalloys: Experiment and phase-field simulation. Acta Mater. 2017, 124, 151–158. [Google Scholar] [CrossRef]










| Loading Diagram | Tension along <001> | Tension along <110> | Tension along <111> |
|---|---|---|---|
 |  |  | |
| Channel 1 | |||
| Channel 2 | |||
| Channel 3 |
| Model | Pros and Cons | Application in the Rafting Analysis |
|---|---|---|
| Phenomenological constitutive models | Pros: Be cost-effective in determining material parameters and applicable in engineering calculations. Cons: Fail to capture the orientation dependence of the mechanical behavior of single crystals; difficult to experimentally verify the hardening rule used in the constitutive models. | Rafting with creep damage [8,19] |
| Physics-based constitutive models | Pros: Be able to model the microstructure evolution and include the contribution of dislocations. Cons: Fail to explicitly capture the motion of dislocations. | Coupling between rafting and crystal plasticity with dislocation densities [67] |
| Discrete dislocation dynamics models | Pros: Explicitly describe the dislocation distribution during microstructural evolution. Cons: Require sufficiently fine grid spacing and great computational cost in simulation. | Distribution of plastic strain in γ-channels and its effect on rafting [16] |
| Continuum dislocation dynamics models | Pros: Consider average distribution of dislocations and need less computational cost. Cons: Difficult to be compared with phenomenological constitutive models in engineering calculations. | Effect of initial dislocation density on rafting [18] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Wang, X.; Yang, F.; Yue, Z.; Li, J.C.M. Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation. Crystals 2020, 10, 1095. https://doi.org/10.3390/cryst10121095
Yu Z, Wang X, Yang F, Yue Z, Li JCM. Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation. Crystals. 2020; 10(12):1095. https://doi.org/10.3390/cryst10121095
Chicago/Turabian StyleYu, Zhiyuan, Xinmei Wang, Fuqian Yang, Zhufeng Yue, and James C. M. Li. 2020. "Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation" Crystals 10, no. 12: 1095. https://doi.org/10.3390/cryst10121095
APA StyleYu, Z., Wang, X., Yang, F., Yue, Z., & Li, J. C. M. (2020). Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation. Crystals, 10(12), 1095. https://doi.org/10.3390/cryst10121095