Tensile Deformation of Ultrafine-Grained Fe-Mn-Al-Ni-C Alloy Studied by In Situ Synchrotron Radiation X-ray Diffraction
Abstract
:1. Introduction
2. Materials and Methods
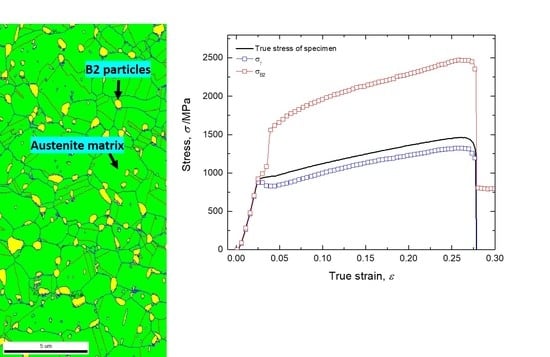
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Furuta, T.; Kuramoto, S.; Ohsuna, T.; Oh-Ishi, K.; Horibuchi, K. Die-hard plastic deformation behavior in an ultrahigh-strength Fe-Ni-Al-C alloy. Scr. Mater. 2015, 101, 87–90. [Google Scholar] [CrossRef]
- Wang, Z.; Baker, I. Effects of annealing and thermo-mechanical treatment on the microstructures and mechanical properties of a carbon-doped FeNiMnAl multi-component alloy. Mater. Sci. Eng. A 2017, 693, 101–110. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Baker, I.; Cai, Z.; Chen, S.; Poplawsky, J.D.; Guo, W. The effect of interstitial carbon on the mechanical properties and dislocation substructure evolution in Fe40.4Ni11.3Mn34.8Al7.5Cr6 high entropy alloys. Acta Mater. 2016, 120, 228–239. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wu, M.; Cai, Z.; Chen, S.; Baker, I. Effect of Ti content on the microstructure and mechanical behavior of (Fe36Ni18Mn33Al13)100−xTix high entropy alloys. Intermet 2016, 75, 79–87. [Google Scholar] [CrossRef] [Green Version]
- Wani, I.S.; Bhattacharjee, T.; Sheikh, S.; Lu, Y.P.; Chatterjee, S.; Bhattacharjee, P.; Guo, S.; Tsuji, N. Ultrafine-Grained AlCoCrFeNi2.1Eutectic High-Entropy Alloy. Mater. Res. Lett. 2016, 4, 174–179. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharjee, T.; Wani, I.S.; Sheikh, S.; Clark, I.T.; Okawa, T.; Guo, S.; Bhattacharjee, P.; Tsuji, N. Simultaneous Strength-Ductility Enhancement of a Nano-Lamellar AlCoCrFeNi2.1 Eutectic High Entropy Alloy by Cryo-Rolling and Annealing. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Tomota, Y.; Lukas, P.; Harjo, S.; Park, J.-H.; Tsuchida, N.; Neov, D. In situ neutron diffraction study of IF and ultra low carbon steels upon tensile deformation. Acta Mater. 2003, 51, 819–830. [Google Scholar] [CrossRef]
- Gao, S.; Bai, Y.; Shibata, A.; Tsuji, N. Microstructures and mechanical property of a Fe-Ni-Al-C alloy containing B2 intermetallic compounds. Mater. Sci. Eng. 2017, 219, 012020. [Google Scholar] [CrossRef] [Green Version]
- Asoo, K.; Tomota, Y.; Harjo, S.; Okitsu, Y. Tensile Behavior of a TRIP-aided Ultra-fine Grained Steel Studied by Neutron Diffraction. ISIJ Int. 2011, 51, 145–150. [Google Scholar] [CrossRef] [Green Version]
- Harjo, S.; Abe, J.; Aizawa, K.; Gong, W.; Iwahashi, T. Deformation Behavior of An Austenitic Steel by Neutron Diffraction. In Proceedings of the Proceedings of the 12th Asia Pacific Physics Conference (APPC12), Makuhari, Japan, 14–19 July 2013; Volume 014017, pp. 1–6. [Google Scholar]
- Fu, S.; Bei, H.; Chen, Y.; Liu, T.; Yu, D.; An, K. Deformation mechanisms and work-hardening behavior of transformation-induced plasticity high entropy alloys by in -situ neutron diffraction. Mater. Res. Lett. 2018, 6, 620–626. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Song, G.; Sisneros, T.A.; Clausen, B.; Pu, C.; Li, L.; Gao, Y.; Liaw, P.K. Load partitioning between the bcc-iron matrix and NiAl-type precipitates in a ferritic alloy on multiple length scales. Sci. Rep. 2016, 6, 23137. [Google Scholar] [CrossRef]
- Saleh, A.A.; Brown, D.W.; Pereloma, E.V.; Clausen, B.; Davies, C.; Tomé, C.N.; Gazder, A.A. An in-situ neutron diffraction study of a multi-phase transformation and twinning-induced plasticity steel during cyclic loading. Appl. Phys. Lett. 2015, 106, 171–911. [Google Scholar] [CrossRef] [Green Version]
- Shibata, A.; Takeda, Y.; Park, N.; Zhao, L.; Harjo, S.; Kawasaki, T.; Gong, W.; Tsuji, N. Nature of dynamic ferrite transformation revealed by in-situ neutron diffraction analysis during thermomechanical processing. Scr. Mater. 2019, 165, 44–49. [Google Scholar] [CrossRef]
- Bae, J.W.; Kim, J.G.; Park, J.M.; Woo, W.; Harjo, S.; Kim, H.S. In situ neutron diffraction study of phase stress evolution in a ferrous medium-entropy alloy under low-temperature tensile loading. Scr. Mater. 2019, 165, 60–63. [Google Scholar] [CrossRef]
- Kim, S.-H.; Kim, H.; Kim, N.J. Brittle intermetallic compound makes ultrastrong low-density steel with large ductility. Nat. Cell Biol. 2015, 518, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Yuan, F.; Xie, Q.; Wang, Y.; Ma, E.; Wu, X. Strain hardening in Fe–16Mn–10Al–0.86C–5Ni high specific strength steel. Acta Mater. 2016, 109, 213–222. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Park, N.; Tian, Y.; Chen, S.; Shibata, A.; Tsuji, N. Novel thermomechanical processing methods for achieving ultragrain refinement of low-carbon steel without heavy plastic deformation. Mater. Res. Lett. 2016, 5, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Miyajima, Y.; Okubo, S.; Miyazawa, T.; Adachi, H.; Fujii, T. In-situ X-ray diffraction during tensile deformation of ultrafine-grained copper using synchrotron radiation. Philos. Mag. Lett. 2016, 96, 294–304. [Google Scholar] [CrossRef]
- Adachi, H.; Miyajima, Y.; Sato, M.; Tsuji, N. Evaluation of dislocation density for 1100 aluminum with different grain size during tensile deformation by using In-situ X-ray diffraction technique. J. Jpn. Inst. Light Met. 2014, 64, 463–469. [Google Scholar] [CrossRef] [Green Version]
- Adachi, H.; Karamatsu, Y.; Nakayama, S.; Miyazawa, T.; Sato, M.; Yamasaki, T. Elastic and Plastic Deformation Behavior Studied by In-Situ Synchrotron X-ray Diffraction in Nanocrystalline Nickel. Mater. Trans. 2016, 57, 1447–1453. [Google Scholar] [CrossRef] [Green Version]
- Hwang, J.; Trang, T.; Lee, O.; Park, G.; Zargaran, A.; Kim, N.J. Improvement of strength – ductility balance of B2-strengthened lightweight steel. Acta Mater. 2020, 191, 1–12. [Google Scholar] [CrossRef]
- Liu, X.; Xue, Q.; Wang, W.; Zhou, L.; Jiang, P.; Ma, H.; Yuan, F.; Wei, Y.; Wu, X. Back-stress-induced strengthening and strain hardening in dual-phase steel. Materialia 2019, 7, 100–376. [Google Scholar] [CrossRef]
- Gao, S.; Chen, M.; Joshi, M.; Shibata, A.; Tsuji, N. Yielding behavior and its effect on uniform elongation in IF steel with various grain sizes. J. Mater. Sci. 2014, 49, 6536–6542. [Google Scholar] [CrossRef]
- Tian, Y.; Gao, S.; Zhao, L.; Lu, S.; Pippan, R.; Zhang, Z.; Tsuji, N. Remarkable transitions of yield behavior and Lüders deformation in pure Cu by changing grain sizes. Scr. Mater. 2018, 142, 88–91. [Google Scholar] [CrossRef]
- Tsuji, N.; Ito, Y.; Saito, Y.; Minamino, Y. Strength and ductility of ultrafine grained aluminum and iron produced by ARB and annealing. Scr. Mater. 2002, 47, 893–899. [Google Scholar] [CrossRef]
- Zheng, R.; Bhattacharjee, T.; Shibata, A.; Sasaki, T.; Hono, K.; Joshi, M.; Tsuji, N. Simultaneously enhanced strength and ductility of Mg-Zn-Zr-Ca alloy with fully recrystallized ultrafine grained structures. Scr. Mater. 2017, 131, 1–5. [Google Scholar] [CrossRef]
- Kamikawa, N.; Huang, X.; Tsuji, N.; Hansen, N. Strengthening mechanisms in nanostructured high-purity aluminium deformed to high strain and annealed. Acta Mater. 2009, 57, 4198–4208. [Google Scholar] [CrossRef]
- Terada, D.; Inoue, S.; Tsuji, N. Microstructure and mechanical properties of commercial purity titanium severely deformed by ARB process. J. Mater. Sci. 2007, 42, 1673–1681. [Google Scholar] [CrossRef]
- Zheng, R.; Du, J.-P.; Gao, S.; Somekawa, H.; Ogata, S.; Tsuji, N. Transition of dominant deformation mode in bulk polycrystalline pure Mg by ultra-grain refinement down to sub-micrometer. Acta Mater. 2020, 198, 35–46. [Google Scholar] [CrossRef]
- Schwab, R. Understanding the complete loss of uniform plastic deformation of some ultrafine-grained metallic materials in tensile straining. Int. J. Plast. 2019, 113, 218–235. [Google Scholar] [CrossRef]
- Schwab, R.; Ruff, V. On the nature of the yield point phenomenon. Acta Mater. 2013, 61, 1798–1808. [Google Scholar] [CrossRef]
- Tsuji, N.; Ogata, S.; Inui, H.; Tanaka, I.; Kishida, K.; Gao, S.; Mao, W.; Bai, Y.; Zheng, R.; Du, J.-P. Strategy for managing both high strength and large ductility in structural materials–sequential nucleation of different deformation modes based on a concept of plaston. Scr. Mater. 2020, 181, 35–42. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, Y.; Wei, Q.; Topping, T.; Dangelewicz, A.; Zhu, Y.; Langdon, T.; Lavernia, E. Influence of specimen dimensions and strain measurement methods on tensile stress–strain curves. Mater. Sci. Eng. A 2009, 525, 68–77. [Google Scholar] [CrossRef]
- De, A.K.; Murdock, D.C.; Mataya, M.C.; Speer, J.G.; Matlock, D.K. Quantitative measurement of deformation-induced martensite in 304 stainless steel by X-ray diffraction. Scr. Mater. 2004, 50, 1445–1449. [Google Scholar] [CrossRef]
- Takaki, S.; Akama, D.; Jiang, F.; Tsuchiyama, T. Correction of the Williamson-Hall Plots by the Diffraction Young’s Modulus. J. Soc. Mater. Sci. Jpn. 2018, 67, 383–388. [Google Scholar] [CrossRef] [Green Version]
- Tomota, Y.; Lukas, P.; Neov, D.; Harjo, S.; Abe, Y. In situ neutron diffraction during tensile deformation of a ferrite-cementite steel. Acta Mater. 2003, 51, 805–817. [Google Scholar] [CrossRef]
- Morooka, S.; Tomota, Y.; Kamiyama, T. Heterogeneous Deformation Behavior Studied by in Situ Neutron Diffraction during Tensile Deformation for Ferrite, Martensite and Pearlite Steels. ISIJ Int. 2008, 48, 525–530. [Google Scholar] [CrossRef] [Green Version]
- Jia, N.; Cong, Z.; Sun, X.; Cheng, S.; Nie, Z.; Ren, Y.; Liaw, P.; Wang, Y.D. An in situ high-energy X-ray diffraction study of micromechanical behavior of multiple phases in advanced high-strength steels. Acta Mater. 2009, 57, 3965–3977. [Google Scholar] [CrossRef]
- Oliver, E.; Daymond, M.R.; Withers, P.J. Interphase and intergranular stress generation in carbon steels. Acta Mater. 2004, 52, 1937–1951. [Google Scholar] [CrossRef]
- Harjo, S.; Tsuchida, N.; Abe, J.; Gong, W. Martensite phase stress and the strengthening mechanism in TRIP steel by neutron diffraction. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Williamson, G.; Hall, W. X-ray line broadening from filed aluminium and wolfram. Acta Met. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Smallman, R.E.; Westmacott, K.H. Stacking faults in face-centred cubic metals and alloys. Philos. Mag. 1957, 2, 669–683. [Google Scholar] [CrossRef]
- Williamson, G.K.; Smallman, R.E. III. Dislocation densities in some annealed and cold-worked metals from measurements on the X-ray debye-scherrer spectrum. Philos. Mag. 1956, 1, 34–46. [Google Scholar] [CrossRef]
- Zhong, Z.Y.; Brokmeier, H.-G.; Gan, W.M.; Maawad, E.; Schwebke, B.; Schell, N. Dislocation density evolution of AA 7020-T6 investigated by in-situ synchrotron diffraction under tensile load. Mater. Charact. 2015, 108, 124–131. [Google Scholar] [CrossRef]
- Dini, G.; Ueji, R.; Najafizadeh, A.; Monir-Vaghefi, S. Flow stress analysis of TWIP steel via the XRD measurement of dislocation density. Mater. Sci. Eng. A 2010, 527, 2759–2763. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Bailey, J.E.; Hirsch, P.B. The dislocation distribution, flow stress, and stored energy in cold-worked polycrystalline silver. Philos. Mag. 1960, 5, 485–497. [Google Scholar] [CrossRef]
- Tian, Y.; Bai, Y.; Zhao, L.; Gao, S.; Yang, H.; Shibata, A.; Zhang, Z.; Tsuji, N. A novel ultrafine-grained Fe 22Mn 0.6C TWIP steel with superior strength and ductility. Mater. Charact. 2017, 126, 74–80. [Google Scholar] [CrossRef]
- Crimp, M.A.; Vedula, K.M. The relationship between cooling rate, grain size and the mechanical behavior of B2 Fe-Al alloys. Mater. Sci. Eng. A 1993, 165, 29–34. [Google Scholar] [CrossRef]
- Yoshida, S.; Bhattacharjee, T.; Bai, Y.; Tsuji, N. Friction stress and Hall-Petch relationship in CoCrNi equi-atomic medium entropy alloy processed by severe plastic deformation and subsequent annealing. Scr. Mater. 2017, 134, 33–36. [Google Scholar] [CrossRef]
- Baker, I.; Nagpal, P.; Liu, F.; Munroe, P. The effect of grain size on the yield strength of FeAl and NiAl. Acta Met. Mater. 1991, 39, 1637–1644. [Google Scholar] [CrossRef]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Yoshimura, T.; Mao, W.; Bai, Y.; Gong, W.; Park, M.-h.; Shibata, A.; Adachi, H.; Sato, M.; Tsuji, N. Tensile Deformation of Ultrafine-Grained Fe-Mn-Al-Ni-C Alloy Studied by In Situ Synchrotron Radiation X-ray Diffraction. Crystals 2020, 10, 1115. https://doi.org/10.3390/cryst10121115
Gao S, Yoshimura T, Mao W, Bai Y, Gong W, Park M-h, Shibata A, Adachi H, Sato M, Tsuji N. Tensile Deformation of Ultrafine-Grained Fe-Mn-Al-Ni-C Alloy Studied by In Situ Synchrotron Radiation X-ray Diffraction. Crystals. 2020; 10(12):1115. https://doi.org/10.3390/cryst10121115
Chicago/Turabian StyleGao, Si, Takuma Yoshimura, Wenqi Mao, Yu Bai, Wu Gong, Myeong-heom Park, Akinobu Shibata, Hiroki Adachi, Masugu Sato, and Nobuhiro Tsuji. 2020. "Tensile Deformation of Ultrafine-Grained Fe-Mn-Al-Ni-C Alloy Studied by In Situ Synchrotron Radiation X-ray Diffraction" Crystals 10, no. 12: 1115. https://doi.org/10.3390/cryst10121115
APA StyleGao, S., Yoshimura, T., Mao, W., Bai, Y., Gong, W., Park, M. -h., Shibata, A., Adachi, H., Sato, M., & Tsuji, N. (2020). Tensile Deformation of Ultrafine-Grained Fe-Mn-Al-Ni-C Alloy Studied by In Situ Synchrotron Radiation X-ray Diffraction. Crystals, 10(12), 1115. https://doi.org/10.3390/cryst10121115