Influence of the Rake Angle on Nanocutting of Fe Single Crystals: A Molecular-Dynamics Study
Abstract
:1. Introduction
2. Simulation Method
3. Results
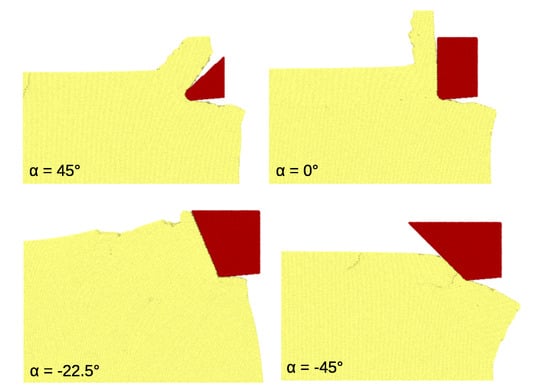
3.1. Plastic Deformation
3.2. Angles
3.3. Chip Thickness
3.4. Forces
3.5. Force Angle
4. Summary
- For the (110)[001] cut system, at not too strongly negative rake angles, the crystal plasticity was governed by a simple mechanism: the evolution of the chip was driven by the generation of edge dislocations with the Burgers vector . These fixed the shear angle to , independently of the rake angle of the tool.
- For positive , the thickness of the cut chip corresponded well to the law predicted by mass conservation, Equation (4).
- While macroscopic cutting of (polycrystalline) iron is governed by a linear relationship between the shear angle and the force angle , in our system, the shear angle was fixed, and also, the force angle was fixed, at . The relation between and was, however, outside that found for macroscopic cutting, Equation (5), of macroscopic (polycrystalline) mild steels and also of other data found experimentally for metal cutting.
- The relation observed between and was even far away from relations derived theoretically, which were shown to hold true in MD simulations of isotropic materials (metallic glasses) [53].
- The chip form was simple—a rectangular shape, showing negligible curvature—as long as a single dislocation glide mechanism governed plasticity. This changed for (strongly) negative rake angles.
- Only for (strongly) negative rake angles, the mechanism of plasticity changed, leading to a complex chip shape or even suppressing the formation of a chip. In these cases, the force angle strongly increased while the friction angle tended to zero.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The (100)[011] Cut System: Twinning


Appendix B. Extended Cutting Length



References
- Fang, F.; Xu, F. Recent Advances in Micro/Nano-cutting: Effect of Tool Edge and Material Properties. Nanomanuf. Metrol. 2018, 1, 4–31. [Google Scholar] [CrossRef]
- Merchant, M.E. Mechanics of the Metal Cutting Process. I. Orthogonal Cutting and a Type 2 Chip. J. Appl. Phys. 1945, 16, 267–275. [Google Scholar] [CrossRef]
- Merchant, M.E. Mechanics of the Metal Cutting Process. II. Plasticity Conditions in Orthogonal Cutting. J. Appl. Phys. 1945, 16, 318–324. [Google Scholar] [CrossRef]
- Astakhov, V.P. On the inadequacy of the single shear plane model of chip formation. Int. J. Mech. Sci. 2005, 47, 1649–1672. [Google Scholar] [CrossRef]
- Oxley, P.L.B. A strain-hardening solution for the “shear angle” in orthogonal metal cutting. Int. J. Mech. Sci. 1961, 3, 68–79. [Google Scholar] [CrossRef]
- Atkins, A.G. Modelling metal cutting using modern ductile fracture mechanics: quantitative explanations for some longstanding problems. Int. J. Mech. Sci. 2003, 45, 373–396. [Google Scholar] [CrossRef]
- Atkins, A.G. Toughness and cutting: A new way of simultaneously determining ductile fracture toughness and strength. Eng. Fract. Mech. 2005, 72, 849–860. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Bringa, E.M.; Gao, Y.; Urbassek, H.M. Molecular dynamics modeling of nanoindentation. In Applied Nanoindentation in Advanced Materials; Tiwari, A., Natarajan, S., Eds.; Wiley: Chichester, UK, 2017; Chapter 14; pp. 313–345. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Alabd Alhafez, I.; Urbassek, H.M. Atomistic Studies of Nanoindentation–A Review of Recent Advances. Crystals 2017, 7, 293. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Brodyanski, A.; Kopnarski, M.; Urbassek, H.M. Nanoscratching of iron: A molecular dynamics study of the influence of surface orientation and scratching direction. Comput. Mater. Sci. 2015, 103, 77–89. [Google Scholar] [CrossRef]
- Alabd Alhafez, I.; Brodyanski, A.; Kopnarski, M.; Urbassek, H.M. Influence of Tip Geometry on Nanoscratching. Tribol. Lett. 2017, 65, 26. [Google Scholar] [CrossRef]
- Komanduri, R.; Chandrasekaran, N.; Raff, L.M. MD simulation of exit failure in nanometric cutting. Mat. Sci. Eng. A 2001, 311, 1. [Google Scholar] [CrossRef]
- Fang, T.H.; Chang, W.J.; Weng, C.I. Nanoindentation and nanomachining characteristics of gold and platinum thin films. Mat. Sci. Eng. A 2006, 430, 332–340. [Google Scholar] [CrossRef]
- Pei, Q.X.; Lu, C.; Fang, F.Z.; Wu, H. Nanometric cutting of copper: A molecular dynamics study. Comput. Mater. Sci. 2006, 37, 434–441. [Google Scholar] [CrossRef]
- Chu, C.Y.; Tan, C.M. Deformation analysis of nanocutting using atomistic model. Int. J. Solids Struct. 2009, 46, 1807–1814. [Google Scholar] [CrossRef] [Green Version]
- Pen, H.M.; Liang, Y.C.; Luo, X.C.; Bai, Q.S.; Goel, S.; Ritchie, J.M. Multiscale simulation of nanometric cutting of single crystal copper and its experimental validation. Comput. Mater. Sci. 2011, 50, 3431–3441. [Google Scholar] [CrossRef] [Green Version]
- Romero, P.A.; Anciaux, G.; Molinari, A.; Molinari, J.F. Friction at the tool-chip interface during orthogonal nanometric machining. Model. Simul. Mater. Sci. Eng. 2012, 20, 055007. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, H.; Dai, L.; Yang, Y.; Du, X.; Tang, P.; Zhang, L. Molecular dynamics simulation of deformation accumulation in repeated nanometric cutting on single crystal copper. RCS Adv. 2015, 5, 12678. [Google Scholar] [CrossRef]
- Narulkar, R.; Bukkapatnam, S.; Raff, L.M.; Komanduri, R. Graphitization as a precursor to wear of diamond in machining pure iron: A molecular dynamics investigation. Comput. Mater. Sci. 2009, 45, 358–366. [Google Scholar] [CrossRef]
- Gao, Y.; Urbassek, H.M. Evolution of plasticity in nanometric cutting of Fe single crystals. Appl. Surf. Sci. 2014, 317, 6–10. [Google Scholar] [CrossRef]
- Alabd Alhafez, I.; Gao, Y.; Urbassek, H.M. Nanocutting: A comparative molecular-dynamics study of fcc, bcc, and hcp metals. Curr. Nanosci. 2017, 13, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Alabd Alhafez, I.; Urbassek, H.M. Orientation dependence in nanocutting of Fe single crystals: A molecular-dynamics study. Comput. Mater. Sci. 2018, 143, 286–294. [Google Scholar] [CrossRef]
- Avila, K.E.; Küchemann, S.; Alabd Alhafez, I.; Urbassek, H.M. An atomistic study of shear-band formation during cutting of metallic glasses. J. Appl. Phys. 2020, 127, 115101. [Google Scholar] [CrossRef]
- Komanduri, R.; Chandrasekaran, N.; Raff, L.M. Molecular dynamics simulation of the nanometric cutting of silicon. Philos. Mag. B 2001, 81, 1989–2019. [Google Scholar] [CrossRef]
- Han, X.S.; Lin, B.; Yu, S.Y.; Wang, S.X. Investigation of tool geometry in nanometric cutting by molecular dynamics simulation. J. Mater. Process. Tech. 2002, 129, 105–108. [Google Scholar] [CrossRef]
- Fang, F.Z.; Wu, H.; Liu, Y.C. Modelling and experimental investigation on nanometric cutting of monocrystalline silicon. Int. J. Mach. Tool Manu. 2005, 45, 1681–1686. [Google Scholar] [CrossRef]
- Cai, M.B.; Li, X.P.; Rahman, M. Study of the temperature and stress in nanoscale ductile mode cutting of silicon using molecular dynamics simulation. J. Mater. Process. Technol. 2007, 192–193, 607–612. [Google Scholar] [CrossRef]
- Lai, M.; Zhang, X.; Fang, F.; Wang, Y.; Feng, M.; Tian, W. Study on nanometric cutting of germanium by molecular dynamics simulation. Nanoscale Res. Lett. 2013, 8, 13. [Google Scholar] [CrossRef] [Green Version]
- Goel, S.; Stukowski, A.; Luo, X.; Agrawal, A.; Reuben, R.L. Anisotropy of single crystal 3C-SiC during nanometric cutting. Model. Simul. Mater. Sci. Eng. 2013, 21, 065004. [Google Scholar] [CrossRef]
- Goel, S.; Kovalchenko, A.; Stukowski, A.; Cross, G. Influence of microstructure on the cutting behaviour of silicon. Acta Mater. 2016, 105, 464–478. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Fang, F.; Zhang, X. Study on surface generation in nano-cutting by large-scale molecular dynamics simulation. Int. J. Adv. Manuf. Technol. 2019, 104, 4325–4329. [Google Scholar] [CrossRef]
- Vardanyan, V.H.; Zhang, Z.; Alabd Alhafez, I.; Urbassek, H.M. Cutting of Al/Si bilayer systems: Molecular dynamics study of twinning, phase transformation, and cracking. Int. J. Adv. Manuf. Technol. 2020, 107, 1297–1307. [Google Scholar] [CrossRef] [Green Version]
- Lai, M.; Zhang, X.D.; Fang, F.Z. Study on critical rake angle in nanometric cutting. Appl. Phys. A 2012, 108, 809–818. [Google Scholar] [CrossRef]
- Hosseini, S.V.; Vahdati, M. Modeling the effect of tool edge radius on contact zone in nanomachining. Comput. Mater. Sci. 2012, 65, 29. [Google Scholar] [CrossRef]
- Xu, F.; Wang, J.; Fang, F.; Zhang, X. A study on the tool edge geometry effect on nano-cutting. Int. J. Adv. Manuf. Technol. 2017, 91, 2787–2797. [Google Scholar] [CrossRef]
- Komanduri, R.; Chandrasekaran, N.; Raff, L.M. Some aspects of machining with negative-rake tools simulating grinding: A molecular dynamics simulation approach. Philos. Mag. B 1999, 79, 955. [Google Scholar] [CrossRef]
- Dai, H.; Du, H.; Chen, J.; Chen, G. Investigation of tool geometry in nanoscale cutting single crystal copper by molecular dynamics simulation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 1208–1220. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Malerba, L.; Marinica, M.C.; Anento, N.; Björkas, C.; Nguyen, H.; Domain, C.; Djurabekova, F.; Olsson, P.; Nordlund, K.; Serra, A.; et al. Comparison of empirical interatomic potentials for iron applied to radiation damage studies. J. Nucl. Mater. 2010, 406, 19–38. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Bringa, E.M.; Kang, K.; Ackland, G.J.; Ruestes, C.J.; Urbassek, H.M. Polycrystalline iron under compression: Plasticity and phase transitions. Phys. Rev. B 2012, 86, 144111. [Google Scholar] [CrossRef]
- Haghighat, S.M.H.; von Pezold, J.; Race, C.P.; Körmann, F.; Friak, M.; Neugebauer, J.; Raabe, D. Influence of the dislocation core on the glide of the 〈111〉{110} edge dislocation in bcc-iron: An embedded atom method study. Comput. Mater. Sci. 2014, 87, 274–282. [Google Scholar] [CrossRef]
- Wagner, R.J.; Ma, L.; Tavazza, F.; Levine, L.E. Dislocation nucleation during nanoindentation of aluminum. J. Appl. Phys. 2008, 104, 114311. [Google Scholar] [CrossRef]
- Banerjee, S.; Naha, S.; Puri, I.K. Molecular simulation of the carbon nanotube growth mode during catalytic synthesis. Appl. Phys. Lett. 2008, 92, 233121. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. Available online: http://lammps.sandia.gov/ (accessed on 13 May 2020). [CrossRef] [Green Version]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 045021. [Google Scholar] [CrossRef]
- Stukowski, A.; Arsenlis, A. On the elastic-plastic decomposition of crystal deformation at the atomic scale. Model. Simul. Mater. Sci. Eng. 2012, 20, 035012. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO –the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. Available online: http://www.ovito.org/ (accessed on 13 May 2020). [CrossRef]
- Henderson, A. ParaView Guide, A Parallel Visualization Application; Kitware Inc.: Clifton Park, NY, USA, 2007; Available online: http://www.paraview.org (accessed on 13 May 2020).
- Krystof, J.; Schallbroch, H. Grundlagen der Zerspanung; Berichte über betriebswissenschaftliche Arbeiten; VDI-Verlag: Berlin, Germany, 1939; Volume 12. [Google Scholar]
- Klocke, F.; König, W. Fertigungsverfahren, 8th ed.; Drehen, Fräsen, Bohren; Springer: Berlin, Germany, 2008; Volume 1. [Google Scholar]
- Pugh, H.L.D. Mechanics of the cutting process. In Proceedings of the Conference on Technology of Engineering Manufacture; The Institute of Mechanical Engineers: London, UK, 1958; pp. 237–254. [Google Scholar]
- Avila, K.E.; Vardanyan, V.H.; Alabd Alhafez, I.; Zimmermann, M.; Kirsch, B.; Urbassek, H.M. Applicability of cutting theory to nanocutting of metallic glasses: Atomistic simulation. 2020. submitted. [Google Scholar]








| (N) | (N) | R (N) | N (N) | (Å) | ||
|---|---|---|---|---|---|---|
| 0.41 | 0.12 | 0.37 | 0.21 | 70.3 | ||
| 0.48 | 0.13 | 0.25 | 0.43 | 39.9 | ||
| 0.69 | 0.18 | 0.18 | 0.69 | 38.0 | ||
| 0.99 | 0.48 | 0.06 | 1.10 | 19.6 | ||
| (*) | 1.01 | 0.48 | 0.06 | 1.12 | 20.0 | |
| 0.60 | 0.66 | 0.04 | 0.89 | 0 | ||
| (*) | 0.56 | 0.60 | 0.03 | 0.82 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhafez, I.A.; Urbassek, H.M. Influence of the Rake Angle on Nanocutting of Fe Single Crystals: A Molecular-Dynamics Study. Crystals 2020, 10, 516. https://doi.org/10.3390/cryst10060516
Alhafez IA, Urbassek HM. Influence of the Rake Angle on Nanocutting of Fe Single Crystals: A Molecular-Dynamics Study. Crystals. 2020; 10(6):516. https://doi.org/10.3390/cryst10060516
Chicago/Turabian StyleAlhafez, Iyad Alabd, and Herbert M. Urbassek. 2020. "Influence of the Rake Angle on Nanocutting of Fe Single Crystals: A Molecular-Dynamics Study" Crystals 10, no. 6: 516. https://doi.org/10.3390/cryst10060516
APA StyleAlhafez, I. A., & Urbassek, H. M. (2020). Influence of the Rake Angle on Nanocutting of Fe Single Crystals: A Molecular-Dynamics Study. Crystals, 10(6), 516. https://doi.org/10.3390/cryst10060516