Grating Coupler Design for Vertical Light Coupling in Silicon Thin Films on Lithium Niobate
Abstract
:1. Introduction
2. Device Design and Methods
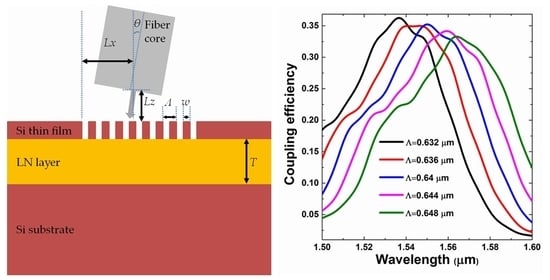
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Witzens, J.; Baehr-Jones, T.; Hochberg, M. Silicon photonics: On-chip OPOs. Nat. Photonics 2010, 4, 10–12. [Google Scholar] [CrossRef]
- Weis, R.S.; Gaylord, T.K. Lithium niobate: Summary of physical properties and crystal structure. Appl. Phys. A 1985, 37, 191–203. [Google Scholar] [CrossRef]
- Lawrence, M. Lithium niobate integrated optics. Rep. Prog. Phys. 1993, 56, 363–429. [Google Scholar] [CrossRef]
- Syms, R.R.A. Advances in channel waveguide lithium niobate integrated optics. Opt. Quant. Electron. 1988, 20, 189–213. [Google Scholar] [CrossRef]
- Rao, A.; Fathpour, S. Compact lithium niobate electrooptic modulators. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 340014. [Google Scholar] [CrossRef]
- Rao, A.; Fathpour, S. Heterogeneous thin-film lithium niobate integrated photonics for electrooptics and nonlinear optics. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 8200912. [Google Scholar] [CrossRef]
- Chiles, J.; Fathpour, S. Mid-infrared integrated waveguide modulators based on silicon-on-lithium-niobate photonics. Optica 2014, 1, 350–355. [Google Scholar] [CrossRef]
- Cao, L.; Aboketaf, A.; Wang, Z.; Preble, S. Hybrid amorphous silicon (a-Si:H)–LiNbO3 electro-optic modulator. Opt. Commun. 2014, 330, 40–44. [Google Scholar] [CrossRef]
- Witmer, J.D.; Hill, J.T.; Safavi-Naeini, A.H. Design of nanobeam photonic crystal resonators for a silicon-on-lithium-niobate platform. Opt. Express 2016, 24, 5876. [Google Scholar] [CrossRef] [Green Version]
- Witmer, J.D.; Valery, J.A.; Arrangoiz-Arriola, P.; Sarabalis, C.J.; Hill, J.T.; Safavi-Naeini, A.H. High-Q photonic resonators and electro-optic coupling using silicon-on-lithium-niobate. Sci. Rep. 2016, 7, 46313. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Xiang, B. Simulation and analysis of electro-optic tunable microring resonators in silicon thin film on lithium niobate. Sci. Rep. 2019, 9, 6302. [Google Scholar] [CrossRef] [PubMed]
- Schmid, B.; Petrov, A.; Eich, M. Optimized grating coupler with fully etched slots. Opt. Express 2009, 17, 11066–11076. [Google Scholar] [PubMed]
- Laere, F.V.; Roelkens, G.; Ayre, M.; Schrauwen, J.; Taillaert, D.; Thourhout, D.V.; Krauss, T.F.; Baets, R. Compact and highly efficient grating couplers between optical fiber and nanophotonic waveguides. J. Lightw. Technol. 2007, 25, 151–156. [Google Scholar] [CrossRef] [Green Version]
- Roelkens, G.; Vermeulen, D.; Thourhout, D.V.; Baets, R.; Brision, S.; Lyan, P.; Gautier, P.; Fédéli, J.M. High efficiency diffractive grating couplers for interfacing a single mode optical fiber with a nanophotonic silicon-on-insulator waveguide circuit. Appl. Phys. Lett. 2008, 92, 131101. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Wang, Y.; Jiang, Y.; Kong, R.; Hu, H. Grating coupler on single-crystal lithium niobate thin film. Opt. Mater. 2017, 72, 136–139. [Google Scholar] [CrossRef]
- Cai, L.; Piazza, G. Low-loss chirped grating for vertical light coupling in lithium niobate on insulator. J. Opt. 2019, 21, 065801. [Google Scholar] [CrossRef]
- Nisar, M.S.; Zhao, X.; Pan, A.; Yuan, S.; Xia, J. Grating coupler for an on-chip lithium niobate ridge waveguide. IEEE Photonics J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Tavlove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Matthew, S.; Shi, R.; Novack, A.; Cher, R.T.P.; Lim, A.E.-J.; Lo, P.G.-Q.; Baehr-Jones, T.; Hochberg, M. A compact bi-wavelength polarization splitting grating coupler fabricated in a 220 nm SOI platform. Opt. Express 2013, 21, 31019–31028. [Google Scholar]
- Wang, Y.; Gao, S.; Wang, K.; Li, H.; Skafidas, E. Ultra-broadband, compact, and high-reflectivity circular Bragg grating mirror based on 220 nm silicon-on-insulator platform. Opt. Express 2017, 25, 6653–6663. [Google Scholar] [CrossRef]
- Vivien, L.; Pascal, D.; Lardenois, S.; Marris-Morini, D.; Cassan, E.; Grillot, F.; Laval, S.; Fédéli, J.-M.; Melhaoui, L.M. Light injection in SOI microwaveguides using high-efficiency grating couplers. J. Lightw. Technol. 2006, 24, 3810–3814. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for absorption of electromagnetic wave. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Suhara, T.; Nishihara, H. Integrated optics components and devices using periodic structures. IEEE J. Quantum Electron. 1986, 22, 845–867. [Google Scholar] [CrossRef] [Green Version]
- Emmons, R.M.; Hall, D.G. Buried-oxide silicon-on-insulator structures. II. Waveguide grating couplers. IEEE J. Quantum Electron. 1992, 28, 164–175. [Google Scholar] [CrossRef]








| T (μm) | Lx (μm) | Ly (μm) | θ (°) | Λ (μm) | DC |
|---|---|---|---|---|---|
| 2.1 | 3.5 | 0 | 8 | 0.64 | 0.829 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Xiang, B. Grating Coupler Design for Vertical Light Coupling in Silicon Thin Films on Lithium Niobate. Crystals 2020, 10, 850. https://doi.org/10.3390/cryst10090850
Han H, Xiang B. Grating Coupler Design for Vertical Light Coupling in Silicon Thin Films on Lithium Niobate. Crystals. 2020; 10(9):850. https://doi.org/10.3390/cryst10090850
Chicago/Turabian StyleHan, Huangpu, and Bingxi Xiang. 2020. "Grating Coupler Design for Vertical Light Coupling in Silicon Thin Films on Lithium Niobate" Crystals 10, no. 9: 850. https://doi.org/10.3390/cryst10090850
APA StyleHan, H., & Xiang, B. (2020). Grating Coupler Design for Vertical Light Coupling in Silicon Thin Films on Lithium Niobate. Crystals, 10(9), 850. https://doi.org/10.3390/cryst10090850