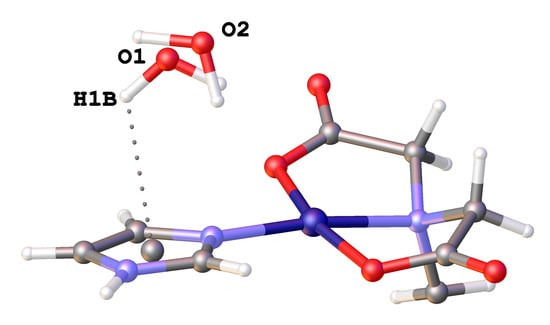
H-Bonds, π-Stacking and (Water)O-H/π Interactions in (µ4-EDTA)Bis(Imidazole) Dicopper(II) Dihydrate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reagents
2.2. Crystallography
2.3. Other Physical Measurements
2.4. Synthesis with Relevant Vis-UV and FTIR Spectral Data
2.5. Theoretical Methods
3. Results and Discussion
3.1. A Comment About the Synthesis of Compound 1
3.2. Thermal Stability
3.3. Copper(II) Coordination and Crystal Structure
3.4. Magnetic Porperties
3.5. DFT Calculations
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, S.; Hoffmann, S.; Prots, Y.; Zhao, J.-T.; Kniep, R. Preparation, Crystal Structures and Thermal Decomposition of Ba2(EDTA) and Ba2(EDTA)·2.5H2O. Z. Anorg. Allg. Chem. 2010, 636, 1710–1715. [Google Scholar] [CrossRef]
- Wu, C.-D.; Guo, Y.-H.; Lin, X.; Wang, S.; Lu, C.-Z.; Zhuang, H.-H. Crystal Structure of Binuclear Oxomolybdenum (V), [Fe(H2O)6][Mo2O4(EDTA)]·5H2O. Jiegou Huaxue 2000, 19, 395–407. [Google Scholar]
- Yin, H.-L.; Zhou, T.-N.; Ao, Y.-Y. Synthesis,Characterization and Structure of a New Partially-sulfided Ni-Mo Dimetallic Complex and Its Evaluation as a Catalyst Precursor for Dibenzothiophene Hydrodesulfurization. Jiegou Huaxue 2015, 34, 1908. [Google Scholar] [CrossRef]
- Liu, H.; Xu, L.; Gao, G.-G.; Li, F.-Y. Two-dimensional Layer Architecture Assembled by Keggin Polyoxotungstate, Cu(II)–EDTA Complex and Sodium Linker: Synthesis, Crystal Structures and Magnetic Properties. J. Solid State Chem. 2007, 180, 1664–1671. [Google Scholar] [CrossRef]
- Polynova, T.N.; Dvorstnova, N.V.; Fillippova, T.V.; Porai-Khosits, M.A.; Nekrasov, Y.V. X-ray Structure Study of Ammonium μ-hexamethylenediaminetetraacetato-bis-(trioxomolybdate) Dihydrate. Koord. Khim. 1986, 12, 1484–1487. [Google Scholar]
- Antsyshkina, A.S.; Sadikov, G.G.; Poznyak, A.L.; Segienko, V.S. Crystal structures of [Cu2(Edta)(Py)2(H2O)2]·2H2O and [Cu(Him)6]{Cu(Im)4[Cu(Edta)(Im)]2}·6H2O, Products of the Interaction of (Ethylenediaminetetraacetato)diaquadicopper(II) with Pyridine and Imidazole. Russ. J. Inorg. Chem. 2006, 51, 241–252. [Google Scholar] [CrossRef]
- Deng, Z.-P.; Gao, S.; Huo, L.-H.; Zhao, H. Synthesis and structure of 2D copper coordination polymer [Cu-2(3-PyOH)(2)(EDTA)](n). Chin. J. Inorg. Chem. 2007, 23, 555. [Google Scholar]
- BRUKER. APEX3 Software v2018.7-2; Bruker AXS Inc.: Madison, WI, USA, 2018. [Google Scholar]
- Sheldrick, G.M. SADABS-Program for Empirical Absorption Correction of Area Detector Data; University of Goettingen: Göttingen, Germany, 1997. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. 2008, A64, 112–122. [Google Scholar] [CrossRef] [Green Version]
- Putz, H.; Brandenburg, K. DIAMOND-Crystal and Molecular Structure Visualization Version 4.6.2; Crystal Impact GbR: Bonn, Germany, 2020. [Google Scholar]
- Young, D.; Ding, F.; Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Zakrzewski, V.G.; et al. Gaussian 16, Revision A.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Rappoport, D.; Furche, F. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 2010, 133, 134105. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Efimenko, Z.M.; Eliseeva, A.A.; Ivanov, D.M.; Galmes, B.; Frontera, A.; Bokach, N.A.; Kukushkin, V.Y. Bifurcated μ2-I···(N,O) Halogen Bonding: The Case of (Nitrosoguanidinate)NiII Cocrystals with Iodine(I)-Based σ-Hole Donors. Cryst. Growth Des. 2020. [Google Scholar] [CrossRef]
- Zelenkov, L.E.; Ivanov, D.M.; Sadykov, E.K.; Bokach, N.A.; Galmes, B.; Frontera, A.; Kukushkin, V.Y. Semicoordination Bond Breaking and Halogen Bond Making Change the Supramolecular Architecture of Metal-Containing Aggregates. Cryst. Growth Des. 2020, 20, 6956–6965. [Google Scholar] [CrossRef]
- Soldatova, N.S.; Postnikov, P.S.; Suslonov, V.V.; Kissler, T.Y.; Ivanov, D.M.; Yusubov, M.S.; Galmes, B.; Frontera, A.; Kukushkin, V.Y. Diaryliodonium as a double σ-hole donor: The dichotomy of thiocyanate halogen bonding provides divergent solid state arylation by diaryliodonium cations. Org. Chem. Front. 2020, 7, 2230–2242. [Google Scholar] [CrossRef]
- Katlenok, E.A.; Haukka, M.; Levin, O.V.; Frontera, A.; Kukushkin, V.Y. Supramolecular Assembly of Metal Complexes by (Aryl)I···dz2 [PtII] Halogen Bonds. Chem. Eur. J. 2020, 26, 7692–7701. [Google Scholar] [CrossRef]
- Rozhkov, A.V.; Eliseeva, A.A.; Baykov, S.V.; Galmes, B.; Frontera, A.; Kukushkin, V.Y. One-Pot Route to X-perfluoroarenes (X = Br, I) Based on FeIII-Assisted C-F Functionalization and Utilization of These Arenes as Building Blocks for Crystal Engineering Involving Halogen Bonding. Cryst. Growth Des. 2020, 20, 5908–5921. [Google Scholar] [CrossRef]
- Rozhkov, A.V.; Ananyev, I.V.; Gomila, R.M.; Frontera, A.; Kukushkin, V.Y. π-Hole···dz2[PtII] Interactions with Electron-Deficient Arenes Enhance the Phosphorescence of PtII-Based Luminophores. Inorg. Chem. 2020, 59, 9308–9314. [Google Scholar] [CrossRef] [PubMed]
- Verdugo-Escamilla, C.; Alarcón-Payer, C.; Frontera, A.; Acebedo-Martínez, F.J.; Domínguez-Martín, A.; Gómez-Morales, J.; Choquesillo-Lazarte, D. Interconvertible Hydrochlorothiazide–Caffeine Multicomponent Pharmaceutical Materials: A Solvent Issue. Crystals 2020, 10, 1088. [Google Scholar] [CrossRef]
- Barbas, R.; Kumar, V.; Vallcorba, O.; Prohens, R.; Frontera, A. Sildenafil–Resorcinol Cocrystal: XRPD Structure and DFT Calculations. Crystals 2020, 10, 1126. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.-P.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theor. Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Bader, R.F.W. A Bond Path: A Universal Indicator of Bonded Interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll Version 13.05.06; TK Gristmill Software: Overland Park, KS, USA, 2013. [Google Scholar]
- Aragay, G.; Hernández, D.; Verdejo, B.; Escudero-Adán, E.C.; Martínez, M.; Ballester, P. Quantification of CH-π Interactions Using Calix[4]pyrrole Receptors as Model Systems. Molecules 2015, 20, 16672–16686. [Google Scholar] [CrossRef] [Green Version]
- Octojić, B.D.; Janjić, G.V.; Zarić, S.D. Parallel Alignment of water and aromatic rings—Crystallographic and Theoretical Evidence for this Interaction. Chem. Commun. 2008, 6546–6548. [Google Scholar] [CrossRef]
- Janjić, G.V.; Malkov, S.N.; Živković, M.V.; Zarić, S.D. What are preferred water-aromatic interactions in proteins and crystal structures of small molecules? Phys. Chem. Chem. Phys. 2014, 16, 23549–23553. [Google Scholar] [CrossRef]
- Hathaway, B.J.; Billing, D.E. The electronic properties and stereochemistry of mono-nuclear complexes of the copper(II) ion. Coord. Chem. Rev. 1970, 5, 143–278. [Google Scholar] [CrossRef]
- Domínguez-Martín, A.; Choquesillo-Lazarte, D.; Dobado, J.A.; Vidal, I.; Lezama, L.; González-Pérez, J.M.; Castiñeiras, A.; Niclós-Gutiérrez, J. From 7-azaindole to adenine: Molecular recognition aspects on mixed-ligand Cu(II) complexes with deaza-adenine ligands. Dalton Trans. 2013, 42, 6119–6130. [Google Scholar] [CrossRef] [PubMed]
- Henke, W.; Kremer, S.; Reinen, D. Cu2+ in Five-Coordination: A Case of a Second-Order Jahn-Teller Effect. 1. Structure and Spectroscopy of the Compounds Cu(terpy)X2· H2O. Inorg. Chem. 1983, 22, 2858–2863. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Kalra, K.; Gorle, S.; Cavallo, L.; Oliva, R.; Chawla, M. Occurrence and Stability of Lone Pair-π and OH-π Interactions between Water and Nucleobases in Functional RNAs. Nucleic Acids Res. 2020, 48, 5825–5838. [Google Scholar] [CrossRef] [PubMed]











| Empirical Formula | C8H12CuN3O5 |
|---|---|
| Empirical formula weight | 293.75 |
| Temperature | 100(2) K |
| Wavelength | 0.71073 Å |
| Crystal system, space group | Monoclinic, C2/c |
| Unit cell dimensions | a = 21.1313(13) Å, α = 90° |
| b = 5.9280(4) Å, β = 110.474(3)° | |
| c = 18.1842(13) Å, γ = 70.545(2)° | |
| Volume | 2134.0(3) Å3 |
| Z, Calculated density | 8, 1.829 Mg/m3 |
| Absorption coefficient | 2.062 mm−1 |
| F(000) | 1200 |
| Crystal size | 0.250 × 0.070 × 0.040 mm2 |
| Theta range for data collection | 3.588 to 30.5050 ° |
| Limiting indices | –28 ≤ h ≤ 30, –8 ≤ k ≤ 8, –25 ≤ l ≤ 25 |
| Reflections collected / unique | 32813 / 3255 [R(int) = 0.0462] |
| Completeness to θ = 25.242 | 99.7% |
| Absorption correction | Semi-empirical from equivalents |
| Max. and min. transmission | 1.000 and 0.857 |
| Refinement method | Full-matrix least-squares on F2 |
| Data/restraints/parameters | 6551/0/307 |
| Goodness-of-fit on F2 | 1.055 |
| Final R indices [I > 2σ(I)] | R1 = 0.0278, wR2 = 0.0619 |
| R indices (all data) | R1 = 0.0354, wR2 = 0.0663 |
| Largest diff. peak and hole | 0.461 and − 0.590 e.Å−3 |
| CCSD ref. number | 2047832 |
| Step or R | Temp. (°C) | Time (min) | Weight (%) Exp. Cal. | Evolved Gases or Residue (R) | |
|---|---|---|---|---|---|
| 1 | 40–210 | 2–19 | 3.366 | 3.066 * | 1 H2O *, CO2 (t) |
| 2 | 210–345 | 19–33 | 33.474 | - | H2O, CO2, CO (t) |
| 3 | 345–400 | 33–38 | 3.704 | - | H2O, CO2, CO, CH4 (t) |
| 4 | 400–425 | 38–42 | 14.307 | - | H2O, CO2, CO, CH4 (t) |
| 5 | 425–515 | 42–51 | 14.817 | - | H2O, CO2, CO, CH4 (t) N2O, NO, NO2 |
| 6 | 515–950 | 51–91 | 1.317 | - | H2O, CO2, CO (t), CH4 (t), N2O, NO, NO2 |
| R | 950 | 95 | 27.088 | 27.080 | 2 CuO |
| Atoms | Distance or Angle |
|---|---|
| Cu(1)-O(11) | 1.9389(12) |
| Cu(1)-N(1) | 1.9451(14) |
| Cu(1)-O(21) | 1.9608(12) |
| Cu(1)-N(10) | 2.0207(14) |
| Cu(1)-O(12)#1 | 2.4878(12) |
| O(11)-Cu(1)-N(1) | 97.23(5) |
| O(11)-Cu(1)-O(21) | 168.16(5) (φ) |
| N(1)-Cu(1)-O(21) | 94.22(5) |
| O(11)-Cu(1)-N(10) | 84.79(5) |
| N(1)-Cu(1)-N(10) | 172.70(5) (θ) |
| O(21)-Cu(1)-N(10) | 84.23(5) |
| O(11)-Cu(1)-O(12)≠1 | 88.90(5) |
| N(1)-Cu(1)-O(12)# 1 | 89.50(5) |
| O(21)-Cu(1)-O(12)#1 | 88.19(5) |
| N(10)-Cu(1)-O(12)#1 | 97.57(5) |
| D-H···A | D(D···A) | <(D-H···A) |
|---|---|---|
| N(3)-H(3)···O(22) ≠ 3 | 2.774(2) | 169.8 |
| O(1)-H1A)···O(12) ≠ 7 | 2.869(4) | 154.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belmont-Sánchez, J.C.; García-Rubiño, M.E.; Frontera, A.; González-Pérez, J.M.; Castiñeiras, A.; Niclós-Gutiérrez, J. H-Bonds, π-Stacking and (Water)O-H/π Interactions in (µ4-EDTA)Bis(Imidazole) Dicopper(II) Dihydrate. Crystals 2021, 11, 48. https://doi.org/10.3390/cryst11010048
Belmont-Sánchez JC, García-Rubiño ME, Frontera A, González-Pérez JM, Castiñeiras A, Niclós-Gutiérrez J. H-Bonds, π-Stacking and (Water)O-H/π Interactions in (µ4-EDTA)Bis(Imidazole) Dicopper(II) Dihydrate. Crystals. 2021; 11(1):48. https://doi.org/10.3390/cryst11010048
Chicago/Turabian StyleBelmont-Sánchez, Jeannette Carolina, María Eugenia García-Rubiño, Antonio Frontera, Josefa María González-Pérez, Alfonso Castiñeiras, and Juan Niclós-Gutiérrez. 2021. "H-Bonds, π-Stacking and (Water)O-H/π Interactions in (µ4-EDTA)Bis(Imidazole) Dicopper(II) Dihydrate" Crystals 11, no. 1: 48. https://doi.org/10.3390/cryst11010048
APA StyleBelmont-Sánchez, J. C., García-Rubiño, M. E., Frontera, A., González-Pérez, J. M., Castiñeiras, A., & Niclós-Gutiérrez, J. (2021). H-Bonds, π-Stacking and (Water)O-H/π Interactions in (µ4-EDTA)Bis(Imidazole) Dicopper(II) Dihydrate. Crystals, 11(1), 48. https://doi.org/10.3390/cryst11010048