Microstructural Changes in Ni-Al-Cr-Based Heat-Resistant Alloy with Re Addition
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
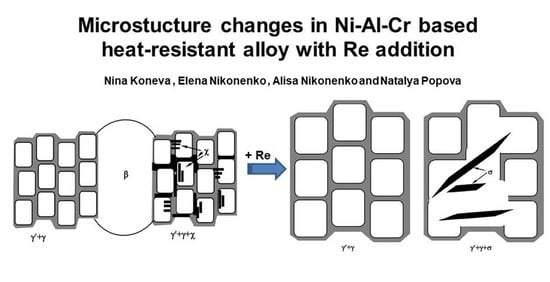
3.1. Phase Composition
3.2. Phase Morphology
3.3. Crystallographic Correspondence of the Primary and Secondary Phases in All States of the Superalloy and the Problem of the Long-Range Stress Field
3.4. Sizes of Quasi-Cuboids, Secondary Phases, and Dislocation Structure
3.5. Scalar Dislocation Density (ρ)
3.6. Phase Transformations during Alloy Annealing after DC
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stoloff, N.S.; Hagel, W.C. Superalloys II; Sims, C.T., Ed.; Wiley-Interscience Publication John Wiley & Sons Publisher: Hoboken, NJ, USA, 1987; p. 615. [Google Scholar]
- Sims, C.T.; Stoloff, N.S.; Hagel, W.C. Superalloys II: High-Temperature Materials for Aerospace and Industrial Power; Metallurgiya Publisher: Moscow, Russia, 1995; Volume 1, p. 385. [Google Scholar]
- Reed, R. The Superalloys: Fundamental and Applications; Cambridge University Press: Cambridge, UK, 2006; p. 363. [Google Scholar]
- Hausmann, D.; Solís, C.; Freund, L.P.; Volz, N.; Heinemann, A.; Göken, M.; Gilles, R.; Neumeier, S. Enhancing the High-Temperature Strength of a Co-Base Superalloy by Optimizing the γ/γ′ Microstructure. Metals 2020, 10, 321. [Google Scholar] [CrossRef] [Green Version]
- Smith, T.; Esser, B.; Antolin, N. Phase transformation strengthening of high-temperature superalloys. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parsa, A.B.; Wollgramm, P.; Buck, H.; Somsen, C.; Kostka, A.; Povstugar, I.; Choi, P.; Raabe, D.; Dlouhy, A.; Müller, J. Advanced Scale Bridging Microstructure Analysis of Single Crystal Ni- Base Superalloys. Adv. Eng. Mater. 2014, 17, 216–230. [Google Scholar] [CrossRef]
- Viswanathan, G.; Shi, R.; Genc, A.; Vorontsov, V.; Kovarik, L.; Rae, C. Segregation at stacking faults within the γ′ phase of two Ni-base superalloys following intermediate temperature creep. Scr. Mater. 2015, 94, 5–8. [Google Scholar] [CrossRef] [Green Version]
- Agudo Jácome, L.; Nörtershäuser, P.; Somsen, C.; Dlouhý, A.; Eggeler, G. On the nature of γ′ phase cutting and its effect on high temperature and low stress creep anisotropy of Nibase single crystal superalloys. Acta Mater. 2014, 69, 246–264. [Google Scholar] [CrossRef]
- Krutz, N.; Shen, C.; Karadge, M.; Egan, A.J.; Bennett, J.R.; Hanlon, T.; Mills, M.J. An Approach Toward Understanding Unstable Gamma Prime Precipitate Evolution and Its Effect on Properties. In Superalloys 2020, The Minerals, Metals & Materials Series; Tin, S., Hardy, M., Clews, J., Cormier, J., Feng, Q., Marcin, J., O’Brien, C., Suzuki, A., Eds.; Springer: Beijing, China, 2020; pp. 691–701. [Google Scholar]
- Kuznetsov, V.P.; Lesnikov, V.P.; Popov, N.A.; Vasil’ev, A.S.; Popova, E.N. Phase Transformations in Single-Crystal Refractory Nickel Alloy with Tantalum, Rhenium and Ruthenium Additions. Metal Sci. Heat Treat. 2018, 60, 100–105. [Google Scholar] [CrossRef]
- Kozlov, E.V.; Nikonenko, E.L.; Popova, N.A.; Koneva, N.A. Structure and composition of higherrhenium-content superalloy based on La-alloyed Ni–Al–Cr. AIP Conf. Proc. 2015, 1683, 020101. [Google Scholar]
- Pollock, T.M. Alloy design for aircraft engines. Nat. Mater. 2016, 15, 809–815. [Google Scholar] [CrossRef] [PubMed]
- Almirall, N.; Wells, P.; Yamamoto, T. Precipitation and hardening in irradiated low alloy steels with a wide range of Ni and Mn compositions. Acta Mater. 2019, 179, 119–128. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, Y.; Marceau, R. Precipitation strengthening of aluminum alloys by room-temperature cyclic plasticity. Science 2019, 2019, 972–975. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, L.; Li, W. High throughput experiment assisted discovery of new Ni-base superalloys. Scr. Mater. 2020, 178, 134–138. [Google Scholar] [CrossRef]
- Barba, D.; Alabort, E.; Pedrazzini, S.; Collins, D.M.; Wilkinson, A.J.; Bagot, P.A.J.; Moody, M.P.; Atkinson, C.; Jérusalem, A.; Reed, R.C. On the microtwinning mechanism in a single crystal superalloy. Acta Mater. 2017, 135, 314–329. [Google Scholar] [CrossRef]
- Seiser, B.; Drautz, R.; Pettifor, D. TCP phase predictions in Ni-based superalloys: Structure maps revisited. Acta Mater. 2011, 59, 749–763. [Google Scholar] [CrossRef]
- Rae, C.M.; Reed, R.C. The precipitation of topologically close-packed phases in rhenium-containing superalloys. Acta Mater. 2001, 49, 4113–4125. [Google Scholar] [CrossRef]
- Kolobov, Y.R.; Kablov, E.N.; Kozlov, E.V. Structure and Properties of Intermetallic Materials with Nano-Phase Hardening; MISiS: Moscow, Russia, 2008; p. 328. [Google Scholar]
- Kozlov, E.V.; Smirnov, A.N.; Nikonenko, E.L.; Popova, N.A.; Koneva, N.A. Phase Morphology and Transformations due to Thermal Treatment of Ni-Al-Cri Ni-Al-Co-based Superalloys. Scale and Concentration Effects; Innovatsionnoe mashinostroenie: Moscow, Russia, 2016; p. 175. [Google Scholar]
- Blavette, D.; Caron, P.; Khan, T. An atom probe investigation of the role of rhenium additions in improving creep resistance of Ni-base superalloys. Scr. Metall. 1986, 20, 1395–1400. [Google Scholar] [CrossRef]
- Mottura, A.; Reed, R.C. What is the role of rhenium in single crystal superalloys? MATEC Web Conf. 2014, 14, 1–6. [Google Scholar] [CrossRef]
- Kozlov, E.V.; Nikonenko, E.L.; Koneva, N.A.; Popova, N.A. Effect of Re Content on Structure and Phase Composition of Ni-Al Alloys. Bull. Russ. Acad. Sci. Phys. 2005, 69, 1116–1120. [Google Scholar]
- Kozlov, E.V.; Popova, N.A.; Kabanina, O.V.; Klimashin, S.I.; Gromov, V.E. The Evolution of Phases State, Defect Structure, Internal Stresses and Redistribution of Carbon and Temper of Cast Structural Steel; Izdatel’stvo SibGIU: Novokuznetsk, Russia, 2007; p. 177. [Google Scholar]
- Saltykov, S.A. Stereometric Metallography; Metallurgy: Moscow, Russia, 1976; p. 271. [Google Scholar]
- Hirsch, P.; Howie, A.; Nicholson, R. Electron Microscopy of Thin Crystals; Mir: Moscow, Russia, 1968; p. 574. [Google Scholar]
- Lyakishev, N.P. Diagrams of Binary Metal Systems; Mechanical engineering: Moscow, Russia, 1996–2000; pp. 1–3. [Google Scholar]
- Cornish, L.A.; Witcomb, M.J. A metallographic study of the Al–Ni–Re phase diagram. J. Alloys Comp. 1999, 291, 145–166. [Google Scholar] [CrossRef]








| Phases | Crystal Lattice Type | Spatial Group | Parameter of Crystal Lattice, nm | Volume Fraction of Phases (±1), % | |
|---|---|---|---|---|---|
| After DC | After DC + Annealing | ||||
| γ′ | Cubic | Pm3m | a = 0.3568–0.3575 | 85.6 | 90.0 |
| γ | Cubic | Fm3m | a = 0.3569 | 8.0 | 9.0 |
| β | Cubic | Pmm | a = 0.288 | 5.0 | 0 |
| χ | Cubic | I3m | a = 0.957–0.960 | 1.4 | 0 |
| σ | Tetragon | P42/mnm | a = 0.910–0.960 c = 0.475–0.499 | 0 | 1.0 |
| The State | Volume Fraction of the State, % | Phase Composition | The Size of Quasi-Cuboids,nm | Particle Size of χ-Phase, nm |
|---|---|---|---|---|
| A | 65 | γ′ + γ | 320 × 440 | - |
| B | 5 | β | - | - |
| C | 30 | γ′ + γ + χ | 320 × 440 | 30 × 240 |
| States | Volume Fraction of States, % | Phase Composition | The Size of Quasi-Cuboids,nm | The Size of σ-Phase Particles, nm |
|---|---|---|---|---|
| A′ | 90 | γ′ + γ | 1440 × 1720 | - |
| B′ | 10 | γ′ + γ + σ | 1440 × 1720 | 290 × 4050 |
| The State of the Alloy | The Width of Interlayers of Ideal Structure (γ′ + γ), μm | The Width of Interlayers with Secondary Phases, μm | The Length of Periodicity, μm |
|---|---|---|---|
| After DC | 120 | 10 | 130 |
| After DC and annealing | 420 | 25 | 445 |
| State of the Alloy | Secondary Phase | ||
|---|---|---|---|
| β-Phase | χ-Phase | σ-Phase | |
| After DC | – | ||
| After DC and annealing | – | – | |
| The State of the Alloy | The Sizes of Quasi-Cuboids of γ′-Phase | The Width of γ-Phase Interlayers, h, nm | Scalar Dislocation Density, ρ⋅10−10, cm−2 | ||
|---|---|---|---|---|---|
| Lateral Size, D, μm | Longitudinal Size, L, μm | in γ′-Phase, ργ′′ | in γ-Phase, ργ | ||
| After DC | 0.32 | 0.44 | 80 | 3.8 | 8.8 |
| After DC+annealing | 1.44 | 1.72 | 170 | 3.0 | 8.3 |
| The State of the Alloy | The Volume Fraction of Ideal γ′-Phase, % | The Volume Fraction of Damaged Mixture γ/γ′, % | The Volume Fraction of β-Phase, % | Phases before and after Transformation |
|---|---|---|---|---|
| After DC | 65 | 30 | - | β+χ |
| After DC and annealing | 90 | 10 | 5 | σ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koneva, N.A.; Nikonenko, E.L.; Nikonenko, A.V.; Popova, N.A. Microstructural Changes in Ni-Al-Cr-Based Heat-Resistant Alloy with Re Addition. Crystals 2021, 11, 89. https://doi.org/10.3390/cryst11020089
Koneva NA, Nikonenko EL, Nikonenko AV, Popova NA. Microstructural Changes in Ni-Al-Cr-Based Heat-Resistant Alloy with Re Addition. Crystals. 2021; 11(2):89. https://doi.org/10.3390/cryst11020089
Chicago/Turabian StyleKoneva, Nina A., Elena L. Nikonenko, Alisa V. Nikonenko, and Natalya A. Popova. 2021. "Microstructural Changes in Ni-Al-Cr-Based Heat-Resistant Alloy with Re Addition" Crystals 11, no. 2: 89. https://doi.org/10.3390/cryst11020089
APA StyleKoneva, N. A., Nikonenko, E. L., Nikonenko, A. V., & Popova, N. A. (2021). Microstructural Changes in Ni-Al-Cr-Based Heat-Resistant Alloy with Re Addition. Crystals, 11(2), 89. https://doi.org/10.3390/cryst11020089