1. Introduction
One of the ways of searching for new crystalline materials is the complication of a chemical composition of crystals with saving of their structure type. Namely, with the transition to an isostructural solid solution, some physical characteristics vary within a wide range. This approach allows one to efficiently control the physicochemical properties and expands the range of promising crystalline materials for various areas of solid-state physics and chemistry. The nonstoichiometric phases
M1−xRxF
2+x (
M = Ca, Sr, Ba;
R = rare earth elements) with the defect fluorite structure are the most commonly used and promising materials in technological applications among known fluoride nonstoichiometric phases. They are formed in 80
MF
2–
RF
3 systems [
1]. The
M1–xRxF
2+x phases have different properties compared to the initial
MF
2, due to their structural features.
According to the modern concept about the structure of nonstoichiometric fluorite phases
M1−xRxF
2+x, the defects formed as a result of heterovalent isomorphic replacement of
M2+ cations by
R3+ cations are grouped into clusters. The anion core of the clusters consists of interstitial anions. According to the principle of local charge compensation, the impurity cations
R3+ are located around the anion core to form cation–anion clusters [
2,
3,
4,
5].
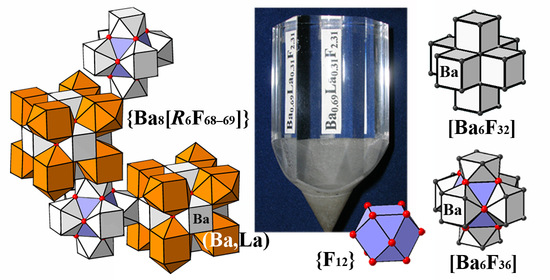
The presence of vacancies in the main anionic motif and interstitial anions in one or more positions is considered to be evidence of cluster formation in the disordered
M1−xRxF
2+x phases. The cuboctahedral groups {F
12} formed by fluorine anions in Wyckoff site 48
i (sp. gr.
) are cores of cation–anion octacubic clusters [
M14−nRnF
64+n] (
Figure 1). The study of the cluster structure based on data on interstitial anions is associated with methodological difficulties in determining light fluorine anions against the background of heavy barium and rare earth cations. The accuracy of determining the occupancies of the positions occupied by the interstitial anions in the
M1−xRxF
2+x structure is quite low.
In early studies of the defect structure of the
M1−xRxF
2+x phases, Wyckoff position 4
a was assumed to be fully occupied with the statistical mixture of the cations (
M1−xRx) [
6]. The reason for this was use of a limited data set, which allowed for localizing interstitial fluorine ions but did not enable to reveal tiny features of a structure such as anharmonic vibrations of ions and displacement of cations from the Wyckoff position 4
a. For the first time, the splitting of the cationic crystallographic Wyckoff site 4
a in the disordered fluorite phases
M1−xRxF
2+x was detected by us in Ba
0.75Lu
0.25F
2.25 [
7].
The tendency toward the positional differentiation is enhanced with an increase in a difference between the ionic radii of the
M2+ and
R3+ cations. The Ba
1−xRxF
2+x (
R = Tm − Lu) solid solutions are characterized by a maximum difference in the sizes of
M2+ and
R3+ cations. We found that in such phases the differentiation of the positions of cations is expressed in a formation of the ordered phases Ba
4R3F
17 (
R = Y, Yb) [
8] with a fluorite-related structure that are formed in the BaF
2–
RF
3 systems with
R = Sm–Lu. In such phases the octacubic clusters transform from disordered defects into elementary structural units (
Figure 2). Long-range order emerges in the spatial arrangement of the clusters.
The cationic motif of the ordered phases is trigonally distorted. Different types of cations occupy various positions, which make it possible to determine their displacements from ideal fluorite positions. The accuracy of determining the cluster structure of the nonstoichiometric phases M1−xRxF2+x based on anionic defects alone is low. The possibility of involving displacements of cations in the refinement of the cluster structure enables one to increase the reliability of the model of the defect structure. For many years, A.M. Golubev successfully developed the idea of extending the cluster structure of ordered phases with a structure derived from the fluorite to the structure of disordered fluorite phases M1−xRxF2+x. The idea is based on the connection between the splitting of the cationic position and the formation of the octacubic clusters.
This work is a continuation of a series of studies [
4,
5] on the investigation of the displacements of cations in the disordered Ba
1−xRxF
2+x (
R = La–Lu) phases. The goal of the study is to complete the investigation of the cationic displacements in Ba
1−xRxF
2+x crystals for the entire rare earth range from La to Lu. This is achieved by selecting the Ba
1−xLa
xF
2+x crystal containing the first member of the rare earth series—La—as the object of this work.
A specific feature of the fluorite phases Ba
1−xRxF
2+x is congruent melting. Such behaviour is anomalous and found only for heterovalent solid solutions with a variable number of atoms in the unit cell. The formation of maxima on Ba
1−xRxF
2+x melting curves was found by [
9] using the differential thermal analysis method for the BaF
2–
RF
3 systems with
R = La–Tb. A rise in the melting point of the congruently melting phase Ba
0.69La
0.31F
2.31 (by 130 K with respect to the melting point of the BaF
2) is the maximum among all congruently melting
M1−xRxF
2+x phases.
The Ba
0.69La
0.31F
2.31 bulk crystals of optical quality can be grown from the melt due to a congruent melting. They are of practical importance as a potential wide band-gap optical material with improved characteristics (compared to the commercially produced BaF
2 single crystals) [
10] and have increased mechanical strength and significant deterioration of cleavage. The possible application of these crystals in a heating–cycling mode requires an understanding of the behavior of their structure during heat treatment. Therefore, a structural study of the Ba
0.69La
0.31F
2.31 crystals annealed at 1173 K for a long time was also performed.
2. Materials and Methods
The Ba0.69La0.31F2.31 single crystal was grown by the Bridgman technique from a melt. The anhydrous BaF2 and LaF3 (99.99%, LANHIT) powders were used as raw materials. The powders were preliminarily annealed in vacuum (~10−2 Pa) for 3–5 h at 450 K and then remelted in a fluorinating CF4 atmosphere. The growth equipment with resistive a graphite heating system and multicellular graphite crucible was applied.
The temperature gradient in the growth zone was ~100 K/cm, crucible pulling rate—5 mm/h and cooling rate of grown crystals ~100 K/h. CF4 (99.999%) was used as a fluorinating agent during growth. Ba0.69La0.31F2.31 single crystals of optical quality were successfully grown with these growth process parameters. Loss of the substance during the crystallization process was about 1 wt.%; no cracks or light-scattering centers were observed.
Postgrowth annealing of Ba0.69La0.31F2.31 crystals was performed in a growth facility at 1173 ± 20 K for 336 h. A fluorinating atmosphere was formed by CF4. The sample for annealing was cut from the middle part of the as-grown crystalline boule (∼0.5 cm3), wrapped in a Ni foil and placed in a graphite crucible. It was located in the near-zero-gradient area of the heater (the axial temperature gradient was less than 5 K/cm). At the end of the heat treatment process, the crucible was cooled by turning off the heater supply and passing a continuous flow of inert gas at room temperature through the volume of the growth chamber. The cooling rate in the initial stage was estimated to be about 200 K/min.
The details of the X-ray diffraction experiment (Xcalibur S Agilent Technologies (Oxford Diffraction), Poland) are listed in
Table 1. An analysis of the diffraction data showed that both crystals belong to the CaF
2 structure type.
The structure was refined within the sp. gr.
using the JANA2006 program [
11]. During refinement, an isotropic extinction correction was introduced into the fitted model according to the Becker–Coppens formalism [
12] (type I, angular distribution of mosaic blocks according to the Gaussian law). When refining the anharmonic components of atomic displacement tensor, the temperature factor was expanded in Gram–Charlier series [
13].
3. Results
Using the method of structural analysis of the M1−xRxF2+x phases, it was found that interstitial fluorine anions appear in difference Fourier syntheses in eight Wyckoff positions: four 32f (w, w, w), two 48i (u, u, 0.5), 48g (q, 0.25, 0.25), 24e (p, 0.5, 0.5) and 4b (0.5, 0.5, 0.5) sp. gr. . The Wyckoff system is used to denote the anions in our work Fint(position)s; s is indicated for the difference of anions in the same position with different coordinates. The matrix anion in Wyckoff site 8c is denoted as F(8c).
The difference Fourier electron density maps for as-grown and annealed Ba
0.69La
0.31F
2.31 single crystals in the (110) plane are shown in
Figure 3. The solid, dotted and long dashed lines in the maps indicate, respectively, positive, negative and zero electron densities. The coordinate grid is given in unit cell fractions. Differences were obtained by subtracting the contributions of ions, Ba
2+ and La
3+ cations, which share the 4
a site in the structure, and matrix anions F
(8c) occupying the Wyckoff position 8
c with refined site occupancy. All atomic displacement parameters were refined in the harmonic approximation.
The difference maps shown in
Figure 3 exhibit pronounced electron density maxima corresponding to interstitial fluorine ions. The maxima in Wyckoff sites 48
i and 4
b are present in the maps of both crystals, which belong to interstitial fluorite ions F
int(48i) и F
int(4b), respectively. The maximum in 32
f in the map of the annealed crystal corresponds to statically displaced matrix F
(8c) anions, which were denoted as F
int(32f)1. The process of shifting matrix anions from their positions is called anionic sublattice relaxation.
The analysis of the displacement of atoms from their crystallographic positions consists in the evaluation of the harmonic and anharmonic thermal vibrations (dynamic displacements) and the analysis of the real displacements (static displacements), which are referred to as the splitting of crystallographic positions. The criterion for applicability of a particular approach is the discrepancy factor.
The character of electron density distribution near the site of the matrix anion F
(8c) in the difference map of the as-grown Ba
0.69La
0.31F
2.31 crystal (
Figure 3a) suggests dynamic displacements of matrix anions. The consideration of anharmonicity of thermal vibrations of F
(8c) anions in this crystal to the third order of expansion in the structure refinement led to complete elimination of the electron density maximum and minimum near the site of the F
(8c) anion in the as-grown phase. In the annealed crystal, the consideration of anharmonicity of thermal vibrations of F
(8c) anion did not lead to any changes in the difference map; thus, it is likely that only static displacements of F
(8c) anions exist in this case.
The distribution of the electron density near the cation position in both crystals (
Figure 3) is characteristic of the static displacement of a part of the cations from Wyckoff position 4
a to 32
f. The attempt to refine the model with the part of Ba
2+ cations being displaced in 32
f was unsuccessful. Implementation of the anharmonic displacement model to thermal vibrations of Ba
2+ and La
3+ cations sharing the 4
a position did not eliminate the maxima and minima of the electron density near the cation position either. The displacement of all La
3+ cations to Wyckoff site 32
f and application of the anharmonic approximation for the thermal oscillations of Ba
2+ cations led to elimination of all heterogeneities in the electron density distribution near Wyckoff site 4
a in the difference Fourier maps of both as-grown and annealed crystals.
In the last stage of refinement, the total number of anions was fixed in correspondence with the composition of each crystal. The coordinates, site occupancy factors and equivalent atomic displacement parameters in the crystals under study are given in
Table 2.
The atomic displacement parameters of the F(8c) anion in as-grown crystal and Ba2+ cation in both crystals were refined within the anharmonic approximation to the third and fourth order of expansion, respectively. The standard deviations for the site occupancies of each atom were calculated with the other refined parameters being fixed.
4. Discussion
According to [
9], no ordered phases were detected in the BaF
2–LaF
3 system. Strictly speaking, one cannot apply any model of an ordered phase for building a model of a structure of the disordered phase Ba
0.69La
0.31F
2.31. Besides, disordered fluorite phases
M1−xRxF
2+x, in contrast to ordered ones
MmRnF
2m+3n, are in a nonequilibrium state. Therefore, the structural unit of the ordered phases may not be strictly repeated in the disordered ones.
Let us assume that the structural model of Ba
0.69La
0.31F
2.31 crystal is based on the octacubic cluster [Ba
14−nLa
nF
64+n], which is an elementary structural unit in Ba
4R3F
17 phases. On the basis of a structure of the ordered phase Ba
4R3F
17, it is possible to propose the formation of anionic groups {F
12} in nonstoichiometric disordered phase Ba
0.69La
0.31F
2.31, which are formed by F
int(48i) anions. The ratio of the number of vacancies (V
(8c)) in the main anionic motif to the number (qF
int(48i)) of interstitial fluorine anions F
int(48i) in both crystals under study is approximately equal to 1.5, which is an additional argument in favor of the formation of the cuboctahedral anionic groups {F
12} in Ba
0.69La
0.31F
2.31 crystals. The fraction of vacancies (V
(8c)) in 8
c positions is calculated from the formula:
where qF
(8c) and qF
int(32f)1 are the numbers of matrix and relaxed anions in 8
c and (32
f)1, respectively.
Other interstitial anions in the ordered phases Ba4R3F17 that correspond to Fint(4b) anions in a disordered one occupy positions in the fluorine cubes outside {F12} groups. In the disordered phase, these anions may be located either outside clusters (inside fluorine cubes) or inside the cuboctahedron {F12}.
The cationic motif in Ba
4R3F
17 is distorted in the way that all
R3+ cations are displaced from the center of the cluster along the four-fold axes, and Ba
2+ cations are shifted towards the center of the cluster along three-fold axes. Based on displacements of cations in the octacubic clusters in Ba
4R3F
17, similar displacements in the disordered phase Ba
0.69La
0.31F
2.31 should be assumed. The results of its structure refinement, however, showed the La
3+ cations being shifted along the three-fold axis instead of Ba
2+. Therefore, we assume that inversed octacubic clusters are formed in both as-grown and annealed crystals in which La
3+ cations are placed in the vertices of a cluster and Ba
2+ in its faces (
Figure 4). Such a cluster was also discovered in Ba
0.88Yb
0.22F
2.22 crystal [
14]. Inversed arrangement of cations in the octacubic cluster is also found in Ba
0.75Lu
0.25F
2.25 [
7] without formation of {F
12} octahedron. The maximum number of
R3+ cations in the octacubic cluster is six.
According to the results of diffraction experiments, the octacubic cluster is formed in the phases Ba
1−xRxF
2+x with
R = La–Nd, Ho–Lu and Y. The dependence of the cluster structure on the type of rare earth element and its concentration for the phases Ba
1−xRxF
2+x has not been systematically studied to date. The dependence of the defect structure on a thermal history of a crystal is crucial in the study of the structure of the
M1−xRxF
2+x fluorite phases. In situ studies of the evolution of the cluster structure of Ca
0.94Y
0.06F
2.06 up to 1200 °C are the most evident [
15].
It is known that the time required to bring a fluorite crystal to an equilibrium state depends on the temperature of the heat treatment [
16]. An in situ experiment does not provide comprehensive information on the dependence of the cluster structure on temperature, since such a study is carried out on crystals that are far from the equilibrium state. The results strongly depend on the duration of an experiment, and for comparison between them, the necessary condition is the unification of the thermal states of the initial crystals. We believe that the most effective method for studying the temperature dependence of the defect structure of the
M1−xRxF
2+x fluorite phases is fixing a thermal state of the crystals at different temperatures by annealing, and then conducting a diffraction experiment at low temperature to reduce thermal vibrations of ions.
This work is the first experimental study of the dependence of the defect structure on the thermal treatment of the Ba1−xRxF2+x phases. The task of the work included the elucidation of possible changes occurring in the cationic and anionic sublattices of Ba0.69La0.31F2.31 during annealing. The authors needed to determine whether the type of the position occupied by interstitial anions and, accordingly, the type of cluster structure changes, and what modifications the atomic displacements of cations and anions undergo.
The changes occurring in the anionic sublattice of the heat-treated Ba0.69La0.31F2.31 crystal consist of a ~1.7-fold decrease in the number of interstitial Fint(4b) anions in the 4b site. During heat treatment, the number of Fint(48i) anions did not change, but their atomic displacement parameter increased, which indicates the deformation of the anionic cuboctahedron {F12} as a result of annealing. In addition, thermal treatment led to the appearance of statically displaced matrix (relaxed) anions in the structure. No changes were found in the cationic sublattice as a result of annealing.
It should be noted that in the process of refining the structure of crystals with high symmetry, such as M1−xRxF2+x phases, strong correlations between refined parameters appear. They do not allow one to obtain occupancies of positions with high accuracy. Occupancies strongly correlate with the atomic displacement parameters, in particular for the positions of La3+ cations and relaxed Fint(32f)1 anions with small distances to neighboring ions. One of the tasks for further research is to conduct a diffraction experiment at low temperature to improve the accuracy of determining the occupancies of positions.
5. Conclusions
The structure of nonstoichiometric fluorite phase Ba0.69La0.31F2.31 in as-grown condition and after a long isothermal annealing at 1173 K was studied by X-ray diffraction.
It was found that the crystals belong to the fluorite structure type.
In both crystals studied, vacancies in the matrix 8c anion position and interstitial fluorine ions at the 48i position (Fint(48i)) were found. The ratio of the number of the Fint(48i) fluorine ions to the number of vacancies is approximately 1.5 in both crystals.
The displacements of the La3+ cations to the 32f site at (w, w, w) with w ≈ 0.023 were found in both as-grown and annealed crystals.
It was established that annealing leads to a change in the type of displacement of the main anions in Wyckoff positions 8c from dynamic to static.
A model of the defect structure of Ba0.69La0.31F2.31 is proposed, according to which interstitial fluorine anions and La3+ cations are aggregated into [Ba14−nLanF64+n] clusters with the cuboctahedral anionic core formed by interstitial fluorine anions in Wyckoff positions 48i. It is proposed that Ba2+ cations are located within the cluster in the centers of the faces, and the La3+ cations are shifted by 0.24 Å from the vertices of the cluster along the three-fold axis towards the center of the cluster.
Investigation of the structure-sensitive properties of Ba0.69La0.31F2.31 crystals in connection with their defect cluster structure is in progress. The solution of this problem will provide the development of an approach to control the characteristics of these type of crystals.