Impurity-Induced Spin-State Crossover in La0.8Sr0.2Co1−xAlxO3
Abstract
:1. Introduction
2. Experimental
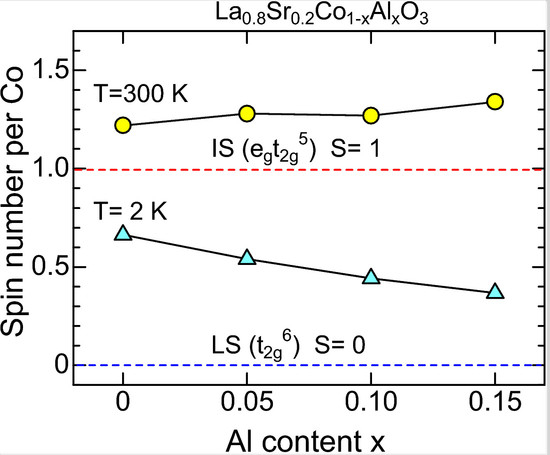
3. Results
4. Discussion
4.1. Effects on Transport Properties
4.2. Comparison with Other Impurities
4.3. An Origin of Impurity-Induced Spin-State Crossover
4.4. Coercive Field Induced by Al Substitution
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gütlich, P.; Garcia, Y.; Goodwin, H.A. Spin crossover phenomena in Fe(II) complexes. Chem. Soc. Rev. 2000, 29, 419–427. [Google Scholar] [CrossRef]
- Sugano, S.; Tanabe, Y.; Kamimura, H. Multiplets of Transition-Metal Ions in Crystals; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Eder, R. Spin-state transition in LaCoO3 by variational cluster approximation. Phys. Rev. B 2010, 81, 035101. [Google Scholar] [CrossRef]
- Jonker, G.; Santen, J.V. Magnetic compounds wtth perovskite structure III. Ferromagnetic compounds of cobalt. Physica 1953, 19, 120–130. [Google Scholar] [CrossRef]
- Raccah, P.M.; Goodenough, J.B. First-order localized-electron collective-electron transition in LaCoO3. Phys. Rev. 1967, 155, 932–943. [Google Scholar] [CrossRef]
- Asai, K.; Yoneda, A.; Yokokura, O.; Tranquada, J.M.; Shirane, G.; Kohn, K. Two spin-state transitions in LaCoO3. J. Phys. Soc. Jpn. 1998, 67, 290–296. [Google Scholar] [CrossRef]
- Vogt, T.; Hriljac, J.A.; Hyatt, N.C.; Woodward, P. Pressure-induced intermediate-to-low spin state transition in LaCoO3. Phys. Rev. B 2003, 67, 140401. [Google Scholar] [CrossRef]
- Kobayashi, W.; Ishiwata, S.; Terasaki, I.; Takano, M.; Grigoraviciute, I.; Yamauchi, H.; Karppinen, M. Room-temperature ferromagnetism in Sr1−xYxCoO3−δ (0.2 ≤ x ≤ 0.25). Phys. Rev. B 2005, 72, 104408. [Google Scholar] [CrossRef]
- Kobayashi, W.; Yoshida, S.; Terasaki, I. High-temperature metallic state of room-temperature ferromagnet Sr1−xYxCoO3−δ. J. Phys. Soc. Jpn. 2006, 75, 103702. [Google Scholar] [CrossRef]
- Golosova, N.O.; Kozlenko, D.P.; Dubrovinsky, L.S.; Drozhzhin, O.A.; Istomin, S.Y.; Savenko, B.N. Spin state and magnetic transformations in Sr0.7Y0.3CoO2.62 at high pressures. Phys. Rev. B 2009, 79, 104431. [Google Scholar] [CrossRef]
- Sheptyakov, D.V.; Pomjakushin, V.Y.; Drozhzhin, O.A.; Istomin, S.Y.; Antipov, E.V.; Bobrikov, I.A.; Balagurov, A.M. Correlation of chemical coordination and magnetic ordering in Sr3YCo4O10.5+δ (δ = 0.02 and 0.26). Phys. Rev. B 2009, 80, 024409. [Google Scholar] [CrossRef]
- Korotin, M.A.; Ezhov, S.Y.; Solovyev, I.V.; Anisimov, V.I.; Khomskii, D.I.; Sawatzky, G.A. Intermediate-spin state and properties of LaCoO3. Phys. Rev. B 1996, 54, 5309–5316. [Google Scholar] [CrossRef]
- Nakao, H.; Murata, T.; Bizen, D.; Murakami, Y.; Ohoyama, K.; Yamada, K.; Ishiwata, S.; Kobayashi, W.; Terasaki, I. Orbital ordering of intermediate-spin state of Co3+ in Sr3YCo4O10.5. J. Phys. Soc. Jpn. 2011, 80, 023711. [Google Scholar] [CrossRef]
- Tokura, Y.; Okimoto, Y.; Yamaguchi, S.; Taniguchi, H.; Kimura, T.; Takagi, H. Thermally induced insulator-metal transition in LaCoO3: A view based on the Mott transition. Phys. Rev. B 1998, 58, R1699–R1702. [Google Scholar] [CrossRef]
- Noguchi, S.; Kawamata, S.; Okuda, K.; Nojiri, H.; Motokawa, M. Evidence for the excited triplet of Co3+ in LaCoO3. Phys. Rev. B 2002, 66, 094404. [Google Scholar] [CrossRef]
- Maris, G.; Ren, Y.; Volotchaev, V.; Zobel, C.; Lorenz, T.; Palstra, T.T.M. Evidence for orbital ordering in LaCoO3. Phys. Rev. B 2003, 67, 224423. [Google Scholar] [CrossRef]
- Haverkort, M.W.; Hu, Z.; Cezar, J.C.; Burnus, T.; Hartmann, H.; Reuther, M.; Zobel, C.; Lorenz, T.; Tanaka, A.; Brookes, N.B.; et al. Spin state transition in LaCoO3 studied using soft X-ray absorption spectroscopy and magnetic circular dichroism. Phys. Rev. Lett. 2006, 97, 176405. [Google Scholar] [CrossRef] [PubMed]
- Klie, R.F.; Zheng, J.C.; Zhu, Y.; Varela, M.; Wu, J.; Leighton, C. Direct measurement of the low-temperature spin-state transition in LaCoO3. Phys. Rev. Lett. 2007, 99, 047203. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, B.; Birol, T.; Haule, K. Role of entropy and structural parameters in the spin-state transition of LaCoO3. Phys. Rev. Mater. 2017, 1, 064403. [Google Scholar] [CrossRef]
- Shimizu, Y.; Takahashi, T.; Yamada, S.; Shimokata, A.; Jin-no, T.; Itoh, M. Symmetry preservation and critical fluctuations in a pseudospin crossover perovskite LaCoO3. Phys. Rev. Lett. 2017, 119, 267203. [Google Scholar] [CrossRef] [PubMed]
- Nasu, J.; Watanabe, T.; Naka, M.; Ishihara, S. Phase diagram and collective excitations in an excitonic insulator from an orbital physics viewpoint. Phys. Rev. B 2016, 93, 205136. [Google Scholar] [CrossRef]
- Sotnikov, A.; Kuneš, J. Field-induced exciton condensation in LaCoO3. Sci. Rep. 2016, 6, 30510. [Google Scholar] [CrossRef] [PubMed]
- Afonso, J.F.; Kuneš, J. Excitonic magnetism in d6 perovskites. Phys. Rev. B 2017, 95, 115131. [Google Scholar] [CrossRef]
- Wang, R.P.; Hariki, A.; Sotnikov, A.; Frati, F.; Okamoto, J.; Huang, H.Y.; Singh, A.; Huang, D.J.; Tomiyasu, K.; Du, C.H.; et al. Excitonic dispersion of the intermediate spin state in LaCoO3 revealed by resonant inelastic X-ray scattering. Phys. Rev. B 2018, 98, 035149. [Google Scholar] [CrossRef]
- Itoh, M.; Natori, I.; Kubota, S.; Motoya, K. Spin-glass behavior and magnetic phase diagram of La1−xSrxCoO3(0 ≤ x ≤ 0.5) studied by magnetization measurements. J. Phys. Soc. Jpn. 1994, 63, 1486–1493. [Google Scholar] [CrossRef]
- Senarís-Rodríguez, M.A.; Goodenough, J.B. Magnetic and transport properties of the system La1−xSrxCoO3−δ (0 < x ≤ 0.50). J. Solid State Chem. 1995, 118, 323–336. [Google Scholar] [CrossRef]
- Masuda, H.; Fujita, T.; Miyashita, T.; Soda, M.; Yasui, Y.; Kobayashi, Y.; Sato, M. Transport and magnetic properties of R1−xAxCoO3 (R = La, Pr and Nd; A = Ba, Sr and Ca). J. Phys. Soc. Jpn. 2003, 72, 873–878. [Google Scholar] [CrossRef]
- Wu, J.; Leighton, C. Glassy ferromagnetism and magnetic phase separation in La1−xSrxCoO3. Phys. Rev. B 2003, 67, 174408. [Google Scholar] [CrossRef]
- Kriener, M.; Zobel, C.; Reichl, A.; Baier, J.; Cwik, M.; Berggold, K.; Kierspel, H.; Zabara, O.; Freimuth, A.; Lorenz, T. Structure, magnetization, and resistivity of La1−xMxCoO3 (M = Ca, Sr, and Ba). Phys. Rev. B 2004, 69, 094417. [Google Scholar] [CrossRef]
- He, C.; Torija, M.A.; Wu, J.; Lynn, J.W.; Zheng, H.; Mitchell, J.F.; Leighton, C. Non-Griffiths-like clustered phase above the Curie temperature of the doped perovskite cobaltite La1−xSrxCoO3. Phys. Rev. B 2007, 76, 014401. [Google Scholar] [CrossRef]
- Podlesnyak, A.; Russina, M.; Furrer, A.; Alfonsov, A.; Vavilova, E.; Kataev, V.; Büchner, B.; Strässle, T.; Pomjakushina, E.; Conder, K.; et al. Spin-state polarons in lightly-hole-doped LaCoO3. Phys. Rev. Lett. 2008, 101, 247603. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, S.; Okimoto, Y.; Taniguchi, H.; Tokura, Y. Spin-state transition and high-spin polarons in LaCoO3. Phys. Rev. B 1996, 53, R2926–R2929. [Google Scholar] [CrossRef]
- Gor’kov, L.P. Theory of superconducitng alloys. In The Physics of Superconductors; Chapter 5; Springer: Berlin, Germany, 2003. [Google Scholar] [CrossRef]
- Fukuzumi, Y.; Mizuhashi, K.; Takenaka, K.; Uchida, S. Universal superconductor-insulator transition and Tc depression in Zn-substituted high-Tc cuprates in the underdoped regime. Phys. Rev. Lett. 1996, 76, 684. [Google Scholar] [CrossRef] [PubMed]
- Kontani, H.; Onari, S. Orbital-fluctuation-mediated superconductivity in iron pnictides: Analysis of the five-orbital Hubbard-Holstein model. Phys. Rev. Lett. 2010, 104, 157001. [Google Scholar] [CrossRef] [PubMed]
- Hagiwara, M.; Katsumata, K.; Affleck, I.; Halperin, B.I.; Renard, J. Observation of S = 1/2 degrees of freedom in an S = 1 linear-chain Heisenberg antiferromagnet. Phys. Rev. Lett. 1990, 65, 3181. [Google Scholar] [CrossRef] [PubMed]
- Masuda, T.; Fujioka, A.; Uchiyama, Y.; Tsukada, I.; Uchinokura, K. Phase transition between dimerized-antiferromagnetic and uniform-antiferromagnetic phases in the impurity-doped spin-Peierls cuprate CuGeO3. Phys. Rev. Lett. 1998, 80, 4566. [Google Scholar] [CrossRef]
- Kyômen, T.; Asaka, Y.; Itoh, M. Negative cooperative effect on the spin-state excitation in LaCoO3. Phys. Rev. B 2003, 67, 144424. [Google Scholar] [CrossRef]
- Asai, S.; Furuta, N.; Yasui, Y.; Terasaki, I. Weak Ferromagnetism in LaCo1−xRhxO3: Anomalous magnetism emerging between two nonmagnetic end phases. J. Phys. Soc. Jpn. 2011, 80, 104705. [Google Scholar] [CrossRef]
- Kimura, S.; Maeda, Y.; Kashiwagi, T.; Yamaguchi, H.; Hagiwara, M.; Yoshida, S.; Terasaki, I.; Kindo, K. Field-induced spin-state transition in the perovskite cobalt oxide Sr1−xYxCoO3−δ. Phys. Rev. B 2008, 78, 180403. [Google Scholar] [CrossRef]
- Smith, R.X.; Hoch, M.J.R.; Moulton, W.G.; Kuhns, P.L.; Reyes, A.P.; Boebinger, G.S.; Zheng, H.; Mitchell, J.F. Evolution of the spin-state transition with doping in La1−xSrxCoO3. Phys. Rev. B 2012, 86, 054428. [Google Scholar] [CrossRef]
- Prakash, R.; Shukla, R.; Nehla, P.; Dhaka, A.; Dhaka, R. Tuning ferromagnetism and spin state in La1−xAxCoO3 (A = Sr, Ca) nanoparticles. J. Alloys Comp. 2018, 764, 379–386. [Google Scholar] [CrossRef]
- Terasaki, I. Thermal conductivity and thermoelectric power of semiconductors. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Koshibae, W.; Tsutsui, K.; Maekawa, S. Thermopower in cobalt oxides. Phys. Rev. B 2000, 62, 6869–6872. [Google Scholar] [CrossRef]
- Terasaki, I.; Sasago, Y.; Uchinokura, K. Large thermoelectric power in NaCo2O4 single crystals. Phys. Rev. B 1997, 56, R12685–R12687. [Google Scholar] [CrossRef]
- Yoshida, S.; Kobayashi, W.; Nakano, T.; Terasaki, I.; Matsubayashi, K.; Uwatoko, Y.; Grigoraviciute, I.; Karppinen, M.; Yamauchi, H. Chemical and physical pressure effects on the magnetic and transport properties of the A-site ordered perovskite Sr3YCo4O10.5. J. Phys. Soc. Jpn. 2009, 78, 094711. [Google Scholar] [CrossRef]
- Terasaki, I.; Shibasaki, S.; Yoshida, S.; Kobayashi, W. Spin State Control of the Perovskite Rh/Co Oxides. Materials 2010, 3, 786–799. [Google Scholar] [CrossRef] [Green Version]
- Asai, S.; Furuta, N.; Okazaki, R.; Yasui, Y.; Terasaki, I. Ga3+ substitution effects in the weak ferromagnetic oxide LaCo0.8Rh0.2O3. Phys. Rev. B 2012, 86, 014421. [Google Scholar] [CrossRef]
- Asai, S.; Okazaki, R.; Terasaki, I.; Yasui, Y.; Kobayashi, W.; Nakao, A.; Kobayashi, K.; Kumai, R.; Nakao, H.; Murakami, Y.; et al. Spin State of Co3+ in LaCo1−xRhxO3 Investigated by Structural Phenomena. J. Phys. Soc. Jpn. 2013, 82, 114606. [Google Scholar] [CrossRef]
- Knizek, K.; Hejtmánek, J.; Marysko, M.; Jirák, Z.; Bursik, J. Stabilization of the high-spin state of Co3+ in LaCo1−xRhxO3. Phys. Rev. B 2012, 85, 134401. [Google Scholar] [CrossRef]
- Terasaki, I.; Asai, S.; Taniguchi, H.; Okazaki, R.; Yasui, Y.; Ikemoto, Y.; Moriwaki, T. Optical evidence for the spin-state disorder in LaCo1−xRhxO3. J. Phys. Condens. Mat. 2017, 29, 235802. [Google Scholar] [CrossRef] [PubMed]
- Sudayama, T.; Nakao, H.; Yamasaki, Y.; Murakami, Y.; Asai, S.; Okazaki, R.; Yasui, Y.; Terasaki, I. Spin state of Co3+ in LaCo1−xRhxO3 studied using X-ray absorption spectroscopy. J. Phys. Soc. Jpn. 2017, 86, 094701. [Google Scholar] [CrossRef]
- Tomiyasu, K.; Kubota, Y.; Shimomura, S.; Onodera, M.; Koyama, S.I.; Nojima, T.; Ishihara, S.; Nakao, H.; Murakami, Y. Spin-state responses to light impurity substitution in low-spin perovskite LaCoO3. Phys. Rev. B 2013, 87, 224409. [Google Scholar] [CrossRef]
- Shibasaki, S.; Terasaki, I.; Nishibori, E.; Sawa, H.; Lybeck, J.; Yamauchi, H.; Karppinen, M. Magnetic and transport properties of the spin-state disordered oxide La0.8Sr0.2Co1−xRhxO3−δ. Phys. Rev. B 2011, 83, 094405. [Google Scholar] [CrossRef]
- Kittel, C. Physical theory of ferromagnetic domains. Rev. Mod. Phys. 1949, 21, 541. [Google Scholar] [CrossRef]
- Kronmüller, H. Theory of the coercive field in amorphous ferromagnetic alloys. J. Mag. Mag. Mater. 1981, 24, 159–167. [Google Scholar] [CrossRef]
- Kneller, E.F.; Luborsky, F.E. Particle size dependence of coercivity and remanence of single-domain particles. J. Appl. Phys. 1963, 34, 656–658. [Google Scholar] [CrossRef]
- Jin, J.; Ohkoshi, S.i.; Hashimoto, K. Giant coercive field of nanometer-sized iron oxide. Adv. Mater. 2004, 16, 48–51. [Google Scholar] [CrossRef]
- Gambardella, P.; Dallmeyer, A.; Maiti, K.; Malagoli, M.C.; Rusponi, S.; Ohresser, P.; Eberhardt, W.; Carbone, C.; Kern, K. Oscillatory magnetic anisotropy in one-dimensional atomic wires. Phys. Rev. Lett. 2004, 93, 077203. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.L.; Drillon, M.; Masciocchi, N.; Sironi, A.; Zhao, J.T.; Rabu, P.; Panissod, P. Ab-initio XRPD crystal structure and giant hysteretic effect (H c= 5.9 T) of a new hybrid terephthalate-based cobalt (II) magnet. Chem. Mater. 2000, 12, 2805–2812. [Google Scholar] [CrossRef]
- Wu, W.; Kiryukhin, V.; Noh, H.J.; Ko, K.T.; Park, J.H.; Ratcliff, W.; Sharma, P.A.; Harrison, N.; Choi, Y.J.; Horibe, Y.; et al. Formation of pancakelike ising domains and giant magnetic coercivity in ferrimagnetic LuFe2O4. Phys. Rev. Lett. 2008, 101, 137203. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, A.; Hashizume, D.; Katori, H.A.; Sasaki, T.; Ohmichi, E.; Nishizaki, T.; Kobayashi, N.; Takagi, H. Ten layered hexagonal perovskite Sr5Ru5−xO15 (x = 0.90), a weak ferromagnet with a giant coercive field Hc ∼ 12 T. Chem. Mater. 2010, 22, 5712–5717. [Google Scholar] [CrossRef]
- Kida, T.; Senda, A.; Yoshii, S.; Hagiwara, M.; Nakano, T.; Terasaki, I. Pressure effect on magnetic properties of a weak ferromagnet BaIrO3. J. Phys. Conf. Ser. 2010, 200, 012084. [Google Scholar] [CrossRef]
- Sato, K.; Bartashevich, M.I.; Goto, T.; Kobayashi, Y.; Suzuki, M.; Asai, K.; Matsuo, A.; Kindo, K. High-field magnetostriction of the spin-state transition compound LaCoO3. J. Phys. Soc. Jpn. 2008, 77, 024601. [Google Scholar] [CrossRef]
- Sato, K.; Matsuo, A.; Kindo, K.; Kobayashi, Y.; Asai, K. Field induced spin-state transition in LaCoO3. J. Phys. Soc. Jpn. 2009, 78, 093702. [Google Scholar] [CrossRef]
- Altarawneh, M.M.; Chern, G.W.; Harrison, N.; Batista, C.D.; Uchida, A.; Jaime, M.; Rickel, D.G.; Crooker, S.A.; Mielke, C.H.; Betts, J.B.; et al. Cascade of magnetic field induced spin transitions in LaCoO3. Phys. Rev. Lett. 2012, 109, 037201. [Google Scholar] [CrossRef] [PubMed]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terasaki, I.; Ikuta, M.; Yamamoto, T.D.; Taniguchi, H. Impurity-Induced Spin-State Crossover in La0.8Sr0.2Co1−xAlxO3. Crystals 2018, 8, 411. https://doi.org/10.3390/cryst8110411
Terasaki I, Ikuta M, Yamamoto TD, Taniguchi H. Impurity-Induced Spin-State Crossover in La0.8Sr0.2Co1−xAlxO3. Crystals. 2018; 8(11):411. https://doi.org/10.3390/cryst8110411
Chicago/Turabian StyleTerasaki, Ichiro, Masamichi Ikuta, Takafumi D. Yamamoto, and Hiroki Taniguchi. 2018. "Impurity-Induced Spin-State Crossover in La0.8Sr0.2Co1−xAlxO3" Crystals 8, no. 11: 411. https://doi.org/10.3390/cryst8110411
APA StyleTerasaki, I., Ikuta, M., Yamamoto, T. D., & Taniguchi, H. (2018). Impurity-Induced Spin-State Crossover in La0.8Sr0.2Co1−xAlxO3. Crystals, 8(11), 411. https://doi.org/10.3390/cryst8110411