Computer Modeling for Single-Screw Extrusion of Wood–Plastic Composites
Abstract
:1. Introduction
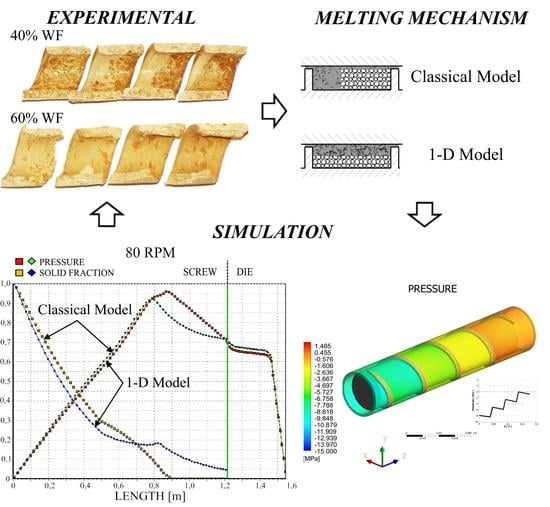
2. Experimental
3. Results
4. Modeling
- –
- Solid conveying, where delay in melting is allowed;
- –
- Melting 1-D or 2-D, depending on the wood flour content;
- –
- Melt conveying in the plasticating unit using 3-D finite element method (FEM)-based screw pumping characteristics;
- –
- Melt flow in the die 1-D or 3-D FEM.
5. Simulations
6. Modeling of Slip Effects
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nova-Institut GmbH. New Market and Trend Report Published. Available online: http://news.bio-based.eu/new-market-and-trend-report-published (accessed on 21 November 2017).
- Bledzki, A.K.; Reihmane, S.; Gassan, J. Thermoplastics Reinforced with Wood Fillers: A Literature Review. Polym. Plast. Technol. Eng. 1998, 37, 451–468. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Misra, M.; Drzal, L.T. Natural Fibers, Biopolymers, and Biocomposites; Taylor & Francis: Boca Raton, FL, USA, 2005; ISBN 978-084-931-741-5. [Google Scholar]
- Klyosov, A.A. Wood-Plastic Composites; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 978-047-014-891-4. [Google Scholar]
- Oksman Niska, K.; Sain, M. Wood-Polymer Composites; Woodhead Publishing Ltd.: Cambridge, UK, 2008; ISBN 978-184-569-272-8. [Google Scholar]
- Zajchowski, S.; Ryszkowska, J. Kompozyty polimerowo-drzewne—Charakterystyka ogólna oraz ich otrzymywanie z materiałów odpadowych. Polimery 2009, 10, 674–682. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Rheological Properties and Their Influence on Extrusion Characteristics of HDPE-Wood Composite Resins. In SPE ANTEK; Society of Plastics Engineers: Houston, TX, USA, 2002; Volume 39, pp. 252–257. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Extrusion Characteristic of HDPE-Wood Composites. In SPE ANTEK; Society of Plastics Engineers: Houston, TX, USA, 2003; Volume 39, pp. 197–201. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Rheological Properties of HDPE-Wood Composites. In SPE ANTEC; Society of Plastics Engineers: Houston, TX, USA, 2003; Volume 39, pp. 975–979. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Extrusion of HDPE-Wood Blends. In SPE ANTEK; Society of Plastics Engineers: Houston, TX, USA, 2004; Volume 40, pp. 448–453. [Google Scholar]
- Li, T.Q.; Wolcott, M.P. Rheology of wood plastics melt. Part 1. Capillary rheometry of HDPE filled with maple. Polym. Eng. Sci. 2005, 45, 549–559. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of wood plastics melt, part 2: Effects of lubricating systems in HDPE/maple composites. Polym. Eng. Sci. 2006, 46, 464–473. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of wood plastics melt, part 3: Nonlinear nature of the flow. Polym. Eng. Sci. 2006, 46, 114–121. [Google Scholar] [CrossRef]
- Hristov, V.; Takács, E.; Vlachopoulos, J. Surface tearing and wall slip phenomena in extrusion of highly filled HDPE/wood flour composites. Polym. Eng. Sci. 2006, 46, 1204–1214. [Google Scholar] [CrossRef]
- Vlachopoulos, J.; Hristov, V. Rheology of Wood Polymer Composites. In Proceedings of the Regional PPS Meeting, Yamagata, Japan, 2–6 July 2006. [Google Scholar]
- Santi, C.R.; Hage, E.; Vlachopoulos, J.; Correa, C.A. Rheology and Processing of HDPE/Wood Flour Composites. Int. Polym. Process. 2009, 24, 346–353. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Behravesh, A.H.; Shakouri, E.; Soury, E. Flow balancing in die design of wood flour/HDPE composite extrusion profiles with consideration of rheological effect. Polym. Eng. Sci. 2010, 50, 543–549. [Google Scholar] [CrossRef]
- Laufer, N.; Hansmann, H.; Koch, M. Rheological Characterisation of the Flow Behaviour of Wood Plastic Composites in Consideration of Different Volume Fractions of Wood. J. Phys. Conf. Ser. 2017, 790, 012017. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Experimental Study for Extrusion of Polypropylene/Wood Flour Composites. Int. Polym. Process. 2015, 30, 113–120. [Google Scholar] [CrossRef]
- Tadmor, Z.; Klein, I. Engineering Principles of Plasticating Extrusion; Van Nostrand Reinhold Co.: New York, NY, USA, 1970; ISBN 978-044-215-635-0. [Google Scholar]
- Ariffin, A.; Ahmad, M.S.B. Review: Single Screw Extruder in Particulate Filler Composite. Polym. Plast. Technol. Eng. 2011, 50, 395–403. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J. Multipurpose Computer Model for Screw Processing of Plastics. Polym. Plast. Technol. Eng. 2012, 51, 626–633. [Google Scholar] [CrossRef]
- Potente, H.; Ridder, H.; Cunha, R.V. Global Concept for Describing and Investigation of Wall Slip Effects in the Extrusion Process. Macromol. Mater. Eng. 2002, 287, 836–842. [Google Scholar] [CrossRef]
- Malik, M.; Kalyon, D.M.; Golba, J.C. Simulation of Co-Rotating Twin Screw Extrusion Process Subject to Pressure-Dependent Wall Slip at Barrel and Screw Surfaces: 3D FEM Analysis for Combinations of Forward- and Reverse-Conveying Screw Elements. Int. Polym. Process. 2014, 29, 51–62. [Google Scholar] [CrossRef]
- Gooneie, A.; Schuschnigg, S.; Duretek, I.; Holzer, C. Numerical simulations of the flow of wood polypropylene composites with wall slipping in a profile die: The significance of material data. In AIP Conference Proceedings 1664; American Institute of Physics: New York, NY, USA, 2015; p. 050014. [Google Scholar]
- Duretek, I.; Schuschnigg, S.; Gooneie, A.; Langecker, G.R.; Holzer, C. Rheological properties of wood polymer composites and their role in extrusion. J. Phys. Conf. Ser. 2015, 602, 012014. [Google Scholar] [CrossRef]
- Maddock, B.H. A Visual Analysis of Flow and Mixing in Extruder Screws. Soc. Plast. Eng. 1959, 15, 383–389. [Google Scholar]
- Street, L.F. Plastifying Extrusion. Intern. Plast. Eng. 1959, 1, 289–296. [Google Scholar]
- Wilczyński, K.; Lewandowski, A.; Wilczyński, K.J. Experimental study for starve-fed single screw extrusion of thermoplastics. Polym. Eng. Sci. 2012, 52, 1258–1270. [Google Scholar] [CrossRef]
- Tadmor, Z. Fundamentals of plasticating extrusion. I. A theoretical model for melting. Polym. Eng. Sci. 1966, 6, 185–190. [Google Scholar] [CrossRef]
- Tadmor, Z.; Duvdevani, I.; Klein, I. Melting in plasticating extuders theory and experiments. Polym. Eng. Sci. 1967, 7, 198–217. [Google Scholar] [CrossRef]
- Altınkaynak, A.; Gupta, M.; Spalding, M.A.; Crabtree, S.L. Melting in a Single Screw Extruder: Experiments and 3D Finite Element Simulations. Int. Polym. Process. 2011, 26, 182–196. [Google Scholar] [CrossRef]
- Agur, E.E.; Vlachopoulos, J. Numerical simulation of a single-screw plasticating extruder. Polym. Eng. Sci. 1982, 22, 1084–1094. [Google Scholar] [CrossRef]
- Vincelette, A.R.; Guerrero, C.S.; Carreau, P.J.; Lafleur, P.G. A Model for Single-screw Plasticating Extruders. Int. Polym. Process. 1989, 4, 232–241. [Google Scholar] [CrossRef]
- Potente, H.; Hanhart, W.; Schöppner, V. Potential Applications for Computer-aided Extruder Design. Int. Polym. Process. 1993, 8, 335–344. [Google Scholar] [CrossRef]
- Wilczyński, K. Single Screw Extrusion Model for Plasticating Extruders. Polym. Plast. Technol. Eng. 1999, 38, 581–608. [Google Scholar] [CrossRef]
- Bawiskar, S.; White, J.L. Solids Conveying and Melting in a Starve Fed Self-wiping Co-rotating Twin Screw Extruder. Int. Polym. Process. 1995, 10, 105–110. [Google Scholar] [CrossRef]
- Bawiskar, S.; White, J.L. Melting model for modular self wiping co-rotating twin screw extruders. Polym. Eng. Sci. 1998, 38, 727–740. [Google Scholar] [CrossRef]
- Sakai, T. The development of on-line techniques and novel processing systems for the monitoring and handling of the evolution of microstructure in nonreactive and reactive polymer systems. Adv. Polym. Technol. 1995, 14, 277–290. [Google Scholar] [CrossRef]
- Potente, H.; Melisch, U. Theoretical and Experimental Investigations of the Melting of Pellets in Co-Rotating Twin-Screw Extruders. Int. Polym. Process. 1996, 11, 101–108. [Google Scholar] [CrossRef]
- Gogos, C.C.; Tadmor, Z.; Kim, M.H. Melting phenomena and mechanisms in polymer processing equipment. Adv. Polym. Technol. 1998, 17, 285–305. [Google Scholar] [CrossRef]
- Vergnes, B.; Delacour, M.L.; Souveton, G.; Bouvier, J.M. A Study of Polymer Melting in a Co-Rotating Twin Screw Extruder. In Proceedings of the International Polymer Processing Society Annual Meeting PPS-15’s, Hertogenbosch, The Netherlands, 31 May–4 June 1999. [Google Scholar]
- Vergnes, B.; Souveton, G.; Delacour, M.L.; Ainser, A. Experimental and Theoretical Study of Polymer Melting in a Co-rotating Twin Screw Extruder. Int. Polym. Process. 2001, 16, 351–362. [Google Scholar] [CrossRef]
- Bawiskar, S.; White, J.L. A Composite Model for Solid Conveying, Melting, Pressure and Fill Factor Profiles in Modular Co. -Rotating Twin Screw Extruders. Int. Polym. Process. 1997, 12, 331–340. [Google Scholar] [CrossRef]
- Vergnes, B.; Valle, G.D.; Delamare, L. A global computer software for polymer flows in corotating twin screw extruders. Polym. Eng. Sci. 1998, 38, 1781–1792. [Google Scholar] [CrossRef]
- Potente, H.; Bastian, M.; Flecke, J. Design of a compounding extruder by means of the SIGMA simulation software. Adv. Polym. Technol. 1999, 18, 147–170. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Experimental Study of Melting in an Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Process. 2001, 16, 257–262. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A.; Wilczyński, K.J. Experimental study of melting of LDPE/PS polyblend in an intermeshing counter-rotating twin screw extruder. Polym. Eng. Sci. 2012, 52, 449–458. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Melting model for intermeshing counter-rotating twin-screw extruders. Polym. Eng. Sci. 2003, 43, 1715–1726. [Google Scholar] [CrossRef]
- Wilczyński, K.; Jiang, Q.; White, J.L. A Composite Model for Melting, Pressure and Fill Factor Profiles in a Metered Fed Closely Intermeshing Counter-rotating Twin Screw Extruder. Int. Polym. Process. 2007, 22, 198–203. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J. Modelowanie przepływu tworzyw w procesie wytłaczania dwuślimakowego przeciwbieżnego, Cz.2. Badania symulacyjne i doświadczalne. Polimery 2011, 56, 45–50. [Google Scholar]
- Jiang, Q.; White, J.L.; Yang, J. A Global Model for Closely Intermeshing Counter-rotating Twin Screw Extruders with Flood Feeding. Int. Polym. Process. 2010, 25, 223–235. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Wilczyński, K.J. Melting Model for Starve Fed Single Screw Extrusion of Thermoplastics. Int. Polym. Process. 2013, 28, 34–42. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A.; Lewandowski, A.; Wilczyński, K. A composite model for starve fed single screw extrusion of thermoplastics. Polym. Eng. Sci. 2014, 54, 2362–2374. [Google Scholar] [CrossRef]
- Ilinca, F.; Hétu, J.F. Three-dimensional Finite Element Solution of the Flow in Single and Twin-Screw Extruders. Int. Polym. Process. 2010, 25, 275–286. [Google Scholar] [CrossRef]
- Teixeira, C.; Gaspar-Cunha, A.; Covas, J.A. Flow and Heat Transfer Along the Length of a Co-rotating Twin Screw Extruder. Polym. Plast. Technol. Eng. 2012, 51, 1567–1577. [Google Scholar] [CrossRef]
- White, J.L.; Potente, H. Screw Extrusion; Carl Hanser Verlag: Munich, Germany, 2003; ISBN 344-619-624-2. [Google Scholar]
- Tadmor, Z.; Gogos, C. Principles of Polymer Processing; Wiley & Sons: New York, NY, USA, 2006; ISBN 047-138-770-3. [Google Scholar]
- Rauwendaal, C. Polymer Extrusion; Hanser: Munich, Germany, 2014; ISBN 978-156-990-516-6. [Google Scholar]
- Campbell, G.A.; Spalding, M.A. One Dimensional Melting in Single-Screw Extruders. In SPE ANTEC; Society of Plastics Engineers: Houston, TX, USA, 2011; Volume 47, pp. 1367–1373. [Google Scholar]
- Wilczyński, K.J.; Lewandowski, A.; Nastaj, A.; Wilczyński, K. Modeling for Starve Fed/Flood Fed Mixing Single-Screw Extruders. Int. Polym. Process. 2016, 31, 82–91. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Nastaj, A.; Wilczyński, K. A Global Model for Starve-Fed Nonconventional Single-Screw Extrusion of Thermoplastics. Adv. Polym. Technol. 2017, 36, 23–35. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A. Study on the Polymer Melt Flow in a Closely Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Process. 2014, 29, 649–659. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A composite model for an intermeshing counter-rotating twin-screw extruder and its experimental verification. Polym. Eng. Sci. 2015, 55, 2838–2848. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Buziak, K. Modelowanie procesu wytlaczania jednoślimakowego polimerowych kompozytów drzewnych przy dozowanym zasilaniu wytłaczarki. Polimery 2018, 63. in press. [Google Scholar]
- Lewandowski, A.; Wilczyński, K. Global Modeling for Single Screw Extrusion with Slip Effects. Int. Polym. Process. 2018, 33. in press. [Google Scholar]
- Ansys Polyflow v. 17. Available online: www.ansys.com (accessed on 7 March 2018).

















| Square-Pitch Screw | |
|---|---|
| Feed/compression/metering sections | 10.78/7.11/9.11 turns |
| Barrel inside diameter, Db | 45 mm |
| Screw pitch | 45 mm |
| Channel depth in feed section, HF | 8 mm |
| Channel depth in metering section, HM | 3 mm |
| Flight width | 5 mm |
| Extruder Operating Conditions | |
| Barrel and die temperature profile | 160/180/190/190/180 °C |
| Frequency of screw rotation | 20, 50, and 80 rpm |
| Material and rheological properties | |
| Density | |
| - bulk, ρbulk | 500 kg/m3 |
| - solid, ρs | 1080 kg/m3 |
| - melt, ρm | 930 kg/m3 |
| Polymer–barrel friction factor | 0.25 |
| Polymer–screw friction factor | 0.15 |
| Heat capacity | |
| - melt, Cpm | 1850 J/(kgK) |
| - solid, Cps | 1160 J/(kgK) |
| Thermal conductivity—melt, km | 0.243 W/(mK) |
| Heat of fusion, λ | 133,850 J/kg |
| Melting temperature, Tm | 125 °C |
| Viscosity, η (see Figure 2, Equation (5)) | |
| - A0 | 12.469780638 |
| - A1 | −0.834550700 |
| - A11 | −0.017832191 |
| - A12 | 0.001331159 |
| - A2 | −0.008413991 |
| - A22 | −0.000025745 |
| where η [Pa∙s], γ̇ [s−1], T [°C] | |
| Experiment | Simulation (See Section 5) | |||
|---|---|---|---|---|
| Screw Speed rpm | Throughput kg/h | Die Pressure MPa | Throughput kg/h | Die Pressure MPa |
| 20 | 7.9 | 10 | 6.6 | 10.7 |
| 50 | 17.4 | 11 | 16.8 | 12.1 |
| 80 | 25.8 | 13 | 27.5 | 12.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilczyński, K.; Buziak, K.; Wilczyński, K.J.; Lewandowski, A.; Nastaj, A. Computer Modeling for Single-Screw Extrusion of Wood–Plastic Composites. Polymers 2018, 10, 295. https://doi.org/10.3390/polym10030295
Wilczyński K, Buziak K, Wilczyński KJ, Lewandowski A, Nastaj A. Computer Modeling for Single-Screw Extrusion of Wood–Plastic Composites. Polymers. 2018; 10(3):295. https://doi.org/10.3390/polym10030295
Chicago/Turabian StyleWilczyński, Krzysztof, Kamila Buziak, Krzysztof J. Wilczyński, Adrian Lewandowski, and Andrzej Nastaj. 2018. "Computer Modeling for Single-Screw Extrusion of Wood–Plastic Composites" Polymers 10, no. 3: 295. https://doi.org/10.3390/polym10030295
APA StyleWilczyński, K., Buziak, K., Wilczyński, K. J., Lewandowski, A., & Nastaj, A. (2018). Computer Modeling for Single-Screw Extrusion of Wood–Plastic Composites. Polymers, 10(3), 295. https://doi.org/10.3390/polym10030295