Grafting-Induced Structural Ordering of Lactide Chains
Abstract
:1. Introduction
2. Model and Simulation Method
3. Results
3.1. Fraction of Backfolded Chains
3.2. Normal and Lateral Density Profiles of the Grafted Chains
3.3. Order Parameter within the Grafted Layer
3.4. Visual Analysis of the Graft’s Conformation
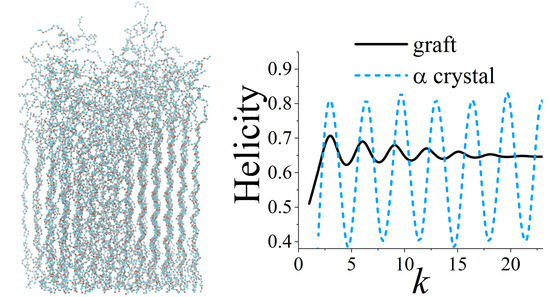
3.5. Helicity of the Grafted Chains
3.6. Influence of Grafting Density on the Structure of the Grafted Layer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kumar, S.K.; Krishnamoorti, R. Nanocomposites: Structure, phase behavior, and properties. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 37–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naskar, A.K.; Keum, J.K.; Boeman, R.G. Polymer matrix nanocomposites for automotive structural components. Nat. Nanotechnol. 2016, 11, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Schadler, L.S. The elusive interphase/interface in polymer nanocomposites. In Comprehensive Composite Materials II; Elsevier: Amsterdam, The Netherland, 2018; pp. 52–72. [Google Scholar]
- Green, P.F. The structure of chain end-grafted nanoparticle/homopolymer nanocomposites. Soft Matter 2011, 7, 7914–7926. [Google Scholar] [CrossRef]
- Kumar, S.K.; Jouault, N.; Benicewicz, B.; Neely, T. Nanocomposites with polymer grafted nanoparticles. Macromolecules 2013, 46, 3199–3214. [Google Scholar] [CrossRef]
- Chen, W.-L.; Cordero, R.; Tran, H.; Ober, C.K. 50th anniversary perspective: Polymer brushes: Novel surfaces for future materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Ginzburg, V.V. Recent developments in theory and modeling of polymer-based nanocomposites. In Problems of Nonlinear Mechanics and Physics of Materials; Springer: Cham, Switzerland, 2019; pp. 205–224. [Google Scholar]
- Lenart, W.R.; Hore, M.J.A. Structure–property relationships of polymer-grafted nanospheres for designing advanced nanocomposites. Nano-Struct. Nano-Objects 2018, 16, 428–440. [Google Scholar] [CrossRef]
- Milner, S.T. Polymer Brushes. Science 1991, 251, 905–914. [Google Scholar] [CrossRef]
- Gay, C. Wetting of a polymer brush by a chemically identical polymer melt. Macromolecules 1997, 30, 5939–5943. [Google Scholar] [CrossRef]
- Borukhov, I.; Leibler, L. Enthalpic stabilization of brush-coated particles in a polymer melt. Macromolecules 2002, 35, 5171–5182. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Ajdari, A.; Leibler, L. Scaling law for entropic effects at interfaces between grafted layers and polymer melts. Macromolecules 1998, 31, 3994–4003. [Google Scholar] [CrossRef]
- Sunday, D.; Ilavsky, J.; Green, D.L. A phase diagram for polymer-grafted nanoparticles in homopolymer matrices. Macromolecules 2012, 45, 4007–4011. [Google Scholar] [CrossRef]
- Kumar, S.K.; Ganesan, V.; Riggleman, R.A. Perspective: Outstanding theoretical questions in polymer-nanoparticle hybrids. J. Chem. Phys. 2017, 147, 020901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Gennes, P.G. Conformations of polymers attached to an interface. Macromolecules 1980, 13, 1069–1075. [Google Scholar] [CrossRef]
- Aubouy, M.; Raphaël, E. Surface-tethered polymers in polymeric matrices. J. Phys. II 1993, 3, 443–448. [Google Scholar] [CrossRef] [Green Version]
- Wijmans, C.M.; Zhulina, E.B.; Fleer, G.J. Effect of free polymer on the structure of a polymer brush and interaction between two polymer brushes. Macromolecules 1994, 27, 3238–3248. [Google Scholar] [CrossRef]
- Glova, A.D.; Falkovich, S.G.; Larin, S.V.; Mezhenskaia, D.A.; Lukasheva, N.V.; Nazarychev, V.M.; Tolmachev, D.A.; Mercurieva, A.A.; Kenny, J.M.; Lyulin, S.V. Poly(lactic acid)-based nanocomposites filled with cellulose nanocrystals with modified surface: All-atom molecular dynamics simulations. Polym. Int. 2016, 65, 892–898. [Google Scholar] [CrossRef]
- Glova, A.D.; Larin, S.V.; Falkovich, S.G.; Nazarychev, V.M.; Tolmachev, D.A.; Lukasheva, N.V.; Lyulin, S.V. Molecular dynamics simulations of oligoester brushes: The origin of unusual conformations. Soft Matter 2017, 13, 6627–6638. [Google Scholar] [CrossRef]
- Birshtein, T.M.; Polotsky, A.A.; Glova, A.D.; Amoskov, V.M.; Mercurieva, A.A.; Nazarychev, V.M.; Lyulin, S.V. How to fold back grafted chains in dipolar brushes. Polymer 2018, 147, 213–224. [Google Scholar] [CrossRef]
- Falkovich, S.G.; Larin, S.V.; Lukasheva, N.V.; Nazarychev, V.M.; Tolmachev, D.A.; Glova, A.D.; Mezhenskaia, D.A.; Kenny, J.M.; Lyulin, S.V. Computational modeling of polylactide and its cellulose-reinforced nanocomposites. In Multifunctional Polymeric Nanocomposites Based on Cellulosic Reinforcements; Elsevier: Amsterdam, The Netherland, 2016; pp. 313–341. [Google Scholar]
- Glova, A.D.; Falkovich, S.G.; Dmitrienko, D.I.; Lyulin, A.V.; Larin, S.V.; Nazarychev, V.M.; Karttunen, M.; Lyulin, S.V. Scale-dependent miscibility of polylactide and polyhydroxybutyrate: molecular dynamics simulations. Macromolecules 2018, 51, 552–563. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- McAliley, J.H.; Bruce, D.A. Development of force field parameters for molecular simulation of polylactide. J. Chem. Theory Comput. 2011, 7, 3756–3767. [Google Scholar] [CrossRef]
- Jorgensen, W.; Maxwell, D.; Tirado-Rives, J. Development and testing of the opls all-atom force-field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Glova, A.D.; Larin, S.V.; Nazarychev, V.M.; Karttunen, M.; Lyulin, S.V. Grafted dipolar chains: Dipoles and restricted freedom lead to unexpected hairpins. Macromolecules. under review.
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Nazarychev, V.M.; Lyulin, A.V.; Larin, S.V.; Gurtovenko, A.A.; Kenny, J.M.; Lyulin, S.V. Molecular dynamics simulations of uniaxial deformation of thermoplastic polyimides. Soft Matter 2016, 12, 3972–3981. [Google Scholar] [CrossRef] [Green Version]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Abraham, M.J.; van der Spoel, D.; Lindahl, E.; Hess, B.; the GROMACS Development Team. Gromacs User Manual Version 5.1.4; GROMACS Development Team: Uppsala, Sweden, 2017; Available online: www.gromacs.org (accessed on 10 December 2019).
- Lukasheva, N.V.; Tolmachev, D.A.; Karttunen, M. Mineralization of phosphorylated cellulose: Crucial role of surface structure and monovalent ions for optimizing calcium content. Phys. Chem. Chem. Phys. 2019, 21, 1067–1077. [Google Scholar] [CrossRef]
- Riniker, S. Fixed-charge atomistic force fields for molecular dynamics simulations in the condensed phase: an overview. J. Chem. Inf. Model. 2018, 58, 565–578. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Nazarychev, V.M.; Lyulin, A.V.; Larin, S.V.; Gofman, I.V.; Kenny, J.M.; Lyulin, S.V. Correlation between the high-temperature local mobility of heterocyclic polyimides and their mechanical properties. Macromolecules 2016, 49, 6700–6710. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Cisneros, G.A.; Karttunen, M.; Ren, P.; Sagui, C. Classical electrostatics for biomolecular simulations. Chem. Rev. 2013, 114, 779–814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falkovich, S.G.; Lyulin, S.V.; Nazarychev, V.M.; Larin, S.V.; Gurtovenko, A.A.; Lukasheva, N.V.; Lyulin, A.V. Influence of the electrostatic interactions on thermophysical properties of polyimides: Molecular-dynamics simulations. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 640–646. [Google Scholar] [CrossRef] [Green Version]
- Nazarychev, V.M.; Larin, S.V.; Yakimansky, A.V.; Lukasheva, N.V.; Gurtovenko, A.A.; Gofman, I.V.; Yudin, V.E.; Svetlichnyi, V.M.; Kenny, J.M.; Lyulin, S.V. Parameterization of electrostatic interactions for molecular dynamics simulations of heterocyclic polymers. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 912–923. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Michaud-Agrawal, N.; Denning, E.J.; Woolf, T.B.; Beckstein, O. MDAnalysis: A toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011, 32, 2319–2327. [Google Scholar] [CrossRef] [Green Version]
- Gowers, R.; Linke, M.; Barnoud, J.; Reddy, T.; Melo, M.; Seyler, S.; Domański, J.; Dotson, D.; Buchoux, S.; Kenney, I.; et al. MDAnalysis: A python package for the rapid analysis of molecular Dynamics simulations. In Proceedings of the 15th Python in Science Conference, Austin, TX, USA, 11–17 July 2016; pp. 98–105. [Google Scholar]
- Deb, D.; Winkler, A.; Yamani, M.H.; Oettel, M.; Virnau, P.; Binder, K. Hard sphere fluids at a soft repulsive wall: A comparative study using Monte Carlo and density functional methods. J. Chem. Phys. 2011, 134, 214706. [Google Scholar] [CrossRef] [Green Version]
- Milchev, A.; Binder, K. Semiflexible polymers grafted to a solid planar substrate: Changing the structure from polymer brush to “polymer bristle”. J. Chem. Phys. 2012, 136, 194901. [Google Scholar] [CrossRef]
- Grest, G.S. Grafted polymer brushes in polymeric matrices. J. Chem. Phys. 1996, 105, 5532–5541. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Structure of a grafted polymer brush: A molecular dynamics simulation. Macromolecules 1989, 22, 4054–4059. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1515–1555. [Google Scholar] [CrossRef]
- Galuschko, A.; Sommer, J.-U. Co-nonsolvency response of a polymer brush: A molecular dynamics study. Macromolecules 2019, 52, 4120–4130. [Google Scholar] [CrossRef]
- Santos, D.E.S.; Li, D.; Ramstedt, M.; Gautrot, J.E.; Soares, T.A. Conformational dynamics and responsiveness of weak and strong polyelectrolyte brushes: Atomistic simulations of poly(dimethyl aminoethyl methacrylate) and poly(2-(methacryloyloxy)ethyl trimethylammonium chloride). Langmuir 2019, 35, 5037–5049. [Google Scholar] [CrossRef] [Green Version]
- Rossi, G.; Elliott, I.G.; Ala-Nissila, T.; Faller, R. Molecular dynamics study of a MARTINI coarse-grained polystyrene brush in good solvent: Structure and dynamics. Macromolecules 2012, 45, 563–571. [Google Scholar] [CrossRef]
- Dimitrov, D.I.; Milchev, A.; Binder, K. Polymer brushes in solvents of variable quality: Molecular dynamics simulations using explicit solvent. J. Chem. Phys. 2007, 127, 084905. [Google Scholar] [CrossRef]
- Glagolev, M.K.; Vasilevskaya, V.V.; Khokhlov, A.R. Compactization of rigid-chain amphiphilic macromolecules with local helical structure. Polym. Sci. Ser. A 2010, 52, 761–774. [Google Scholar] [CrossRef]
- Borzdun, N.I.; Larin, S.V.; Falkovich, S.G.; Nazarychev, V.M.; Volgin, I.V.; Yakimansky, A.V.; Lyulin, A.V.; Negi, V.; Bobbert, P.A.; Lyulin, S.V. Molecular dynamics simulation of poly(3-hexylthiophene) helical structure in vacuo and in amorphous polymer surrounding. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 2448–2456. [Google Scholar] [CrossRef] [Green Version]
- Farah, S.; Anderson, D.G. Physical and mechanical properties of PLA, and their functions in widespread applications—A comprehensive review. Adv. Drug Deliv. Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef] [Green Version]
- Androsch, R.; Schick, C.; Di Lorenzo, M.L. Melting of conformationally disordered crystals (α’-phase) of poly(l-lactic acid). Macromol. Chem. Phys. 2014, 215, 1134–1139. [Google Scholar] [CrossRef]
- Wasanasuk, K.; Tashiro, K.; Hanesaka, M.; Ohhara, T.; Kurihara, K.; Kuroki, R.; Tamada, T.; Ozeki, T.; Kanamoto, T. Crystal structure analysis of poly(l-lactic acid) α-form on the basis of the 2-dimensional wide-angle synchrotron X-ray and neutron diffraction measurements. Macromolecules 2011, 44, 6441–6452. [Google Scholar] [CrossRef]
- Garlotta, D. A Literature Review of Poly(Lactic Acid). J. Polym. Environ. 2001, 9, 63–84. [Google Scholar] [CrossRef]
- Kalish, J.P.; Zeng, X.; Yang, X.; Hsu, S.L. A spectroscopic analysis of conformational distortion in the α’ phase of poly(lactic acid). Polymer 2011, 52, 3431–3436. [Google Scholar] [CrossRef]
- Sasaki, S.; Asakura, T. Helix distortion and crystal structure of the α-form of poly(l-lactide). Macromolecules 2003, 36, 8385–8390. [Google Scholar] [CrossRef]
- Auras, R.; Harte, B.; Selke, S. An overview of polylactides as packaging materials. Macromol. Biosci. 2004, 4, 835–864. [Google Scholar] [CrossRef]
- Hore, M.J.A. Polymers on nanoparticles: Structure & dynamics. Soft Matter 2019, 15, 1120–1134. [Google Scholar]
- Poling-Skutvik, R.; Olafson, K.N.; Narayanan, S.; Stingaciu, L.; Faraone, A.; Conrad, J.C.; Krishnamoorti, R. confined dynamics of grafted polymer chains in solutions of linear polymer. Macromolecules 2017, 50, 7372–7379. [Google Scholar] [CrossRef]











© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glova, A.D.; Melnikova, S.D.; Mercurieva, A.A.; Larin, S.V.; Lyulin, S.V. Grafting-Induced Structural Ordering of Lactide Chains. Polymers 2019, 11, 2056. https://doi.org/10.3390/polym11122056
Glova AD, Melnikova SD, Mercurieva AA, Larin SV, Lyulin SV. Grafting-Induced Structural Ordering of Lactide Chains. Polymers. 2019; 11(12):2056. https://doi.org/10.3390/polym11122056
Chicago/Turabian StyleGlova, Artyom D., Sofya D. Melnikova, Anna A. Mercurieva, Sergey V. Larin, and Sergey V. Lyulin. 2019. "Grafting-Induced Structural Ordering of Lactide Chains" Polymers 11, no. 12: 2056. https://doi.org/10.3390/polym11122056
APA StyleGlova, A. D., Melnikova, S. D., Mercurieva, A. A., Larin, S. V., & Lyulin, S. V. (2019). Grafting-Induced Structural Ordering of Lactide Chains. Polymers, 11(12), 2056. https://doi.org/10.3390/polym11122056