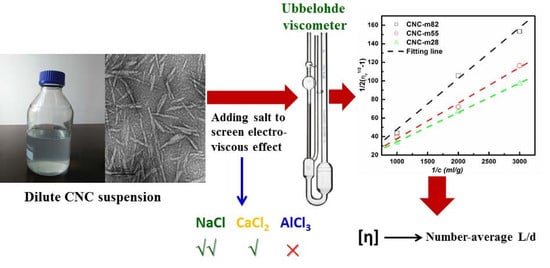
Estimation of Aspect Ratio of Cellulose Nanocrystals by Viscosity Measurement: Influence of Aspect Ratio Distribution and Ionic Strength
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. CNC Preparation
2.3. Transmission Electron Microscopy (TEM)
2.4. Zeta Potential Measurement
2.5. Viscosity Measurement
2.6. Aspect Ratio Estimation
3. Results and Discussion
3.1. Morphology of CNC
3.2. CNC Aspect Ratio Prediction by Viscosity Measurement
3.3. Influence of Aspect Ratio Distribution
3.4. Influence of Ionic Strength
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grishkewich, N.; Mohammed, N.; Tang, J.; Tam, K.C. Recent advances in the application of cellulose nanocrystals. Curr. Opin. Colloid Interface Sci. 2017, 29, 32–45. [Google Scholar] [CrossRef]
- Jonoobi, M.; Oladi, R.; Davoudpour, Y.; Oksman, K.; Dufresne, A.; Hamzeh, Y.; Davoodi, R. Different preparation methods and properties of nanostructured cellulose from various natural resources and residues: A review. Cellulose 2015, 22, 935–969. [Google Scholar] [CrossRef]
- Mariano, M.; El Kissi, N.; Dufresne, A. Cellulose nanocrystals and related nanocomposites: Review of some properties and challenges. J. Polym. Sci. Part B 2014, 52, 791–806. [Google Scholar] [CrossRef]
- Habibi, Y. Key advances in the chemical modification of nanocelluloses. Chem. Soc. Rev. 2014, 43, 1519–1542. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wu, Q.; Zheng, M.; Li, Q.; Wang, S.; Zhang, C. Mechanical, thermal properties and curing kinetics of liquid silicone rubber filled with cellulose nanocrystal. Cellulose 2018, 25, 473–483. [Google Scholar] [CrossRef]
- Mariano, M.; El Kissi, N.; Dufresne, A. Cellulose nanocrystal reinforced oxidized natural rubber nanocomposites. Carbohydr. Polym. 2016, 137, 174–183. [Google Scholar] [CrossRef] [PubMed]
- Siqueira, G.; Bras, J.; Dufresne, A. Cellulosic bionanocomposites: A review of preparation, properties and applications. Polymers 2010, 2, 728–765. [Google Scholar] [CrossRef]
- Sharma, A.; Thakur, M.; Bhattacharya, M.; Mandal, T.; Goswami, S. Commercial application of cellulose nano-composites—A review. Biotechnol. Rep. 2019, 21, e00316. [Google Scholar] [CrossRef] [PubMed]
- Oksman, K.; Aitomaki, Y.; Mathew, A.P.; Siqueira, G.; Zhou, Q.; Butylina, S.; Tanpichai, S.; Zhou, X.J.; Hooshmand, S. Review of the recent developments in cellulose nanocomposite processing. Compos. Part A 2016, 83, 2–18. [Google Scholar] [CrossRef]
- Domingues, R.M.A.; Gomes, M.E.; Reis, R.L. The potential of cellulose nanocrystals in tissue engineering strategies. Biomacromolecules 2014, 15, 2327–2346. [Google Scholar] [CrossRef] [PubMed]
- Li, W.Y.; Lu, S.C.; Zhao, M.C.; Lin, X.X.; Zhang, M.; Xiao, H.; Liu, K.; Huang, L.L.; Chen, L.H.; Ouyang, X.H.; et al. Self-healing cellulose nanocrystals-containing gels via reshuffling of thiuram disulfide bonds. Polymers 2018, 10, 1392. [Google Scholar] [CrossRef]
- Zubik, K.; Singhsa, P.; Wang, Y.A.; Manuspiya, H.; Narain, R. Thermo-responsive Poly(N-Isopropylacrylamide)-Cellulose nanocrystals hybrid hydrogels for wound dressing. Polymers 2017, 9, 119. [Google Scholar] [CrossRef]
- Li, F.; Biagioni, P.; Bollani, M.; Maccagnan, A.; Piergiovanni, L. Multi-functional coating of cellulose nanocrystals for flexible packaging applications. Cellulose 2013, 20, 2491–2504. [Google Scholar] [CrossRef]
- Santos, T.M.; Souza Filho, M.d.S.M.; Caceres, C.A.; Rosa, M.F.; Morais, J.P.S.; Pinto, A.M.B.; Azeredo, H.M.C. Fish gelatin films as affected by cellulose whiskers and sonication. Food Hydrocoll. 2014, 41, 113–118. [Google Scholar] [CrossRef]
- Dai, L.L.; Li, W.; Cao, J.; Li, B.; Liu, S.X. Formation, tuning and application of chiral nematic liquid crystal phase based on nanocrystalline cellulose. Prog. Chem. 2015, 27, 861–869. [Google Scholar]
- Zhao, Y.; Gao, G.Z.; Liu, D.G.; Tian, D.L.; Zhu, Y.Y.; Chang, Y. Vapor sensing with color-tunable multilayered coatings of cellulose nanocrystals. Carbohydr. Polym. 2017, 174, 39–47. [Google Scholar] [CrossRef]
- Kim, D.H.; Song, Y.S. Anisotropic optical film embedded with cellulose nanowhisker. Carbohydr. Polym. 2015, 130, 448–454. [Google Scholar] [CrossRef]
- Kabir, A.; Dunlop, M.J.; Acharya, B.; Bissessur, R.; Ahmed, M. Polymeric composites with embedded nanocrystalline cellulose for the removal of iron(II) from contaminated water. Polymers 2018, 10, 1377. [Google Scholar] [CrossRef]
- Parra-Vasquez, A.N.G.; Stepanek, I.; Davis, V.A.; Moore, V.C.; Haroz, E.H.; Shaver, J.; Hauge, R.H.; Smalley, R.E.; Pasquali, M. Simple length determination of single-walled carbon nanotubes by viscosity measurements in dilute suspensions. Macromolecules 2007, 40, 4043–4047. [Google Scholar] [CrossRef]
- Wierenga, A.M.; Philipse, A.P. Low-Shear viscosities of dilute dispersions of colloidal rodlike silica particles in cyclohexane. J. Colloid Interface Sci. 1996, 180, 360–370. [Google Scholar] [CrossRef]
- Xu, Y.; Atrens, A.D.; Stokes, J.R. Rheology and microstructure of aqueous suspensions of nanocrystalline cellulose rods. J. Colloid Interface Sci. 2017, 496, 130–140. [Google Scholar] [CrossRef]
- Wu, Q.; Meng, Y.; Wang, S.; Li, Y.; Fu, S.; Ma, L.; Harper, D. Rheological behavior of cellulose nanocrystal suspension: Influence of concentration and aspect ratio. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Shafiei-Sabet, S.; Hamad, W.Y.; Hatzikiriakos, S.G. Rheology of nanocrystalline cellulose aqueous suspensions. Langmuir 2012, 28, 17124–17133. [Google Scholar] [CrossRef]
- Lu, A.; Hemraz, U.; Khalili, Z.; Boluk, Y. Unique viscoelastic behaviors of colloidal nanocrystalline cellulose aqueous suspensions. Cellulose 2014, 21, 1239–1250. [Google Scholar] [CrossRef]
- Bercea, M.; Navard, P. Shear dynamics of aqueous suspensions of cellulose whiskers. Macromolecules 2000, 33, 6011–6016. [Google Scholar] [CrossRef]
- Li, M.C.; Wu, Q.L.; Song, K.L.; Lee, S.; Qing, Y.; Wu, Y.Q. Cellulose nanoparticles: Structure-morphology-rheology relationships. ACS Sustain. Chem. Eng. 2015, 3, 821–832. [Google Scholar] [CrossRef]
- Tanaka, R.; Saito, T.; Ishii, D.; Isogai, A. Determination of nanocellulose fibril length by shear viscosity measurement. Cellulose 2014, 21, 1581–1589. [Google Scholar] [CrossRef]
- Meng, Y.; Wu, Q.; Young, T.M.; Huang, B.; Wang, S.; Li, Y. Analyzing three-dimensional structure and geometrical shape of individual cellulose nanocrystal from switchgrass. Polym. Compos. 2015, 38, 2368–2377. [Google Scholar] [CrossRef]
- Tanaka, R.; Saito, T.; Hondo, H.; Isogai, A. Influence of flexibility and dimensions of nanocelluloses on the flow properties of their aqueous dispersions. Biomacromolecules 2015, 16, 2127–2131. [Google Scholar] [CrossRef]
- Wu, Q.; Li, X.; Fu, S.; Li, Q.; Wang, S. Estimation of aspect ratio of cellulose nanocrystals by viscosity measurement: Influence of surface charge density and NaCl concentration. Cellulose 2017, 24, 3255–3264. [Google Scholar] [CrossRef]
- Boluk, Y.; Lahiji, R.; Zhao, L.; McDermott, M.T. Suspension viscosities and shape parameter of cellulose nanocrystals (CNC). Colloids Surf. A Physicochem. Eng. Asp. 2011, 377, 297–303. [Google Scholar] [CrossRef]
- Lenfant, G.; Heuzey, M.C.; van de Ven, T.G.M.; Carreau, P.J. Intrinsic viscosity of suspensions of electrosterically stabilized nanocrystals of cellulose. Cellulose 2015, 22, 1109–1122. [Google Scholar] [CrossRef]
- Elazzouzi-Hafraoui, S.; Nishiyama, Y.; Putaux, J.-L.; Heux, L.; Dubreuil, F.; Rochas, C. The shape and size distribution of crystalline nanoparticles prepared by acid hydrolysis of native cellulose. Biomacromolecules 2008, 9, 57–65. [Google Scholar] [CrossRef]
- Bai, W.; Holbery, J.; Li, K. A technique for production of nanocrystalline cellulose with a narrow size distribution. Cellulose 2009, 16, 455–465. [Google Scholar] [CrossRef]
- Das, K.; Ray, D.; Bandyopadhyay, N.R.; Ghosh, T.; Mohanty, A.K.; Misra, M. A study of the mechanical, thermal and morphological properties of microcrystalline cellulose particles prepared from cotton slivers using different acid concentrations. Cellulose 2009, 16, 783–793. [Google Scholar] [CrossRef]
- Sharma, P.R.; Joshi, R.; Sharma, S.K.; Hsiao, B.S. A simple approach to prepare carboxycellulose nanofibers from untreated biomass. Biomacromolecules 2017, 18, 2333–2342. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.R.; Zheng, B.Q.; Sharma, S.K.; Zhan, C.B.; Wang, R.F.; Bhatia, S.R.; Hsiao, B.S. High aspect ratio carboxycellulose nanofibers prepared by nitro-oxidation method and their nanopaper properties. ACS Appl. Nano Mater. 2018, 1, 3969–3980. [Google Scholar] [CrossRef]
- Geng, L.H.; Mittal, N.; Zhan, C.B.; Ansari, F.; Sharma, P.R.; Peng, X.F.; Hsiao, B.S.; Soderberg, L.D. Understanding the mechanistic behavior of highly charged cellulose nanofibers in aqueous systems. Macromolecules 2018, 51, 1498–1506. [Google Scholar] [CrossRef]
- Geng, L.H.; Peng, X.F.; Zhan, C.B.; Naderi, A.; Sharma, P.R.; Mao, Y.M.; Hsiao, B.S. Structure characterization of cellulose nanofiber hydrogel as functions of concentration and ionic strength. Cellulose 2017, 24, 5417–5429. [Google Scholar] [CrossRef]
- Ubbelohde, L. Arrangement for Testing the Viscosity of Liquid Materials. U.S. Patent 2,091,896, 31 August 1937. [Google Scholar]
- Fedors, R.F. A method for estimating both the solubility parameters and molar volumes of liquids. Supplement. Polym. Eng. Sci. 1974, 14, 472. [Google Scholar] [CrossRef]
- Larson, R.G. The Structure and Rheology of Complex Fluid; Oxford Univeristy Press: New York, NY, USA, 1999. [Google Scholar]
- Batchelor, G.K. The stress system in a suspension of force-free particles. J. Fluid Mech. 1970, 41, 545–570. [Google Scholar] [CrossRef]
- Jowkarderis, L.; van de Ven, T.G.M. Intrinsic viscosity of aqueous suspensions of cellulose nanofibrils. Cellulose 2014, 21, 2511–2517. [Google Scholar] [CrossRef]
- Masruchin, N.; Park, B.D.; Causin, V.; Um, I.C. Characteristics of TEMPO-oxidized cellulose fibril-based hydrogels induced by cationic ions and their properties. Cellulose 2015, 22, 1993–2010. [Google Scholar] [CrossRef]
- Dong, H.; Snyder, J.F.; Williams, K.S.; Andzelm, J.W. Cation-induced hydrogels of cellulose nanofibrils with tunable moduli. Biomacromolecules 2013, 14, 3338–3345. [Google Scholar] [CrossRef]






| NaCl Concentration (mM) | CNC-A | CNC-B | ||
|---|---|---|---|---|
| [η] (mL/g) | L/d | [η] (mL/g) | L/d | |
| 0 | 120 | 40 | 344 | 73 |
| 1.0 | 21 | 14 | 76 | 30 |
| Samples | m1/m2 | n1/n2 | Pm | Pn | [η] (mL/g) (Experiment) | L/d (Experiment) |
|---|---|---|---|---|---|---|
| CNC-m28 | 2:8 | 0.166:1 | 28.3 | 29.3 | 75 | 30 |
| CNC-m55 | 5:5 | 0.664:1 | 22.9 | 24.7 | 55 | 28 |
| CNC-m82 | 8:2 | 2.66:1 | 17.5 | 18.8 | 33 | 18 |
| NaCl Concentration (mM) | [η] (mL/g) | L/d | CaCl2 Concentration (mM) | [η] (mL/g) | L/d | AlCl3 Concentration (mM) | [η] (mL/g) | L/d |
|---|---|---|---|---|---|---|---|---|
| 0 | 120 | 40 | 0 | 120 | 40 | 0 | 120 | 40 |
| 0.5 | 25 | 16 | 0.05 | 37 | 20 | 0.01 | 34 | 19 |
| 1.0 | 21 | 14 | 0.1 | 32 | 18 | 0.02 | 21 | 14 |
| 3.0 | 29 | 17 | 0.2 | 20 | 14 | 0.05 | 22 | 14 |
| 5.0 | 40 | 21 | 0.4 | 26 | 16 | 0.07 | 24 | 18 |
| 10.0 | 45 | 23 | 0.8 | 52 | 24 | 0.10 | 68 | 29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Li, X.; Li, Q.; Wang, S.; Luo, Y. Estimation of Aspect Ratio of Cellulose Nanocrystals by Viscosity Measurement: Influence of Aspect Ratio Distribution and Ionic Strength. Polymers 2019, 11, 781. https://doi.org/10.3390/polym11050781
Wu Q, Li X, Li Q, Wang S, Luo Y. Estimation of Aspect Ratio of Cellulose Nanocrystals by Viscosity Measurement: Influence of Aspect Ratio Distribution and Ionic Strength. Polymers. 2019; 11(5):781. https://doi.org/10.3390/polym11050781
Chicago/Turabian StyleWu, Qiang, Xiuwen Li, Qian Li, Siqun Wang, and Yan Luo. 2019. "Estimation of Aspect Ratio of Cellulose Nanocrystals by Viscosity Measurement: Influence of Aspect Ratio Distribution and Ionic Strength" Polymers 11, no. 5: 781. https://doi.org/10.3390/polym11050781
APA StyleWu, Q., Li, X., Li, Q., Wang, S., & Luo, Y. (2019). Estimation of Aspect Ratio of Cellulose Nanocrystals by Viscosity Measurement: Influence of Aspect Ratio Distribution and Ionic Strength. Polymers, 11(5), 781. https://doi.org/10.3390/polym11050781