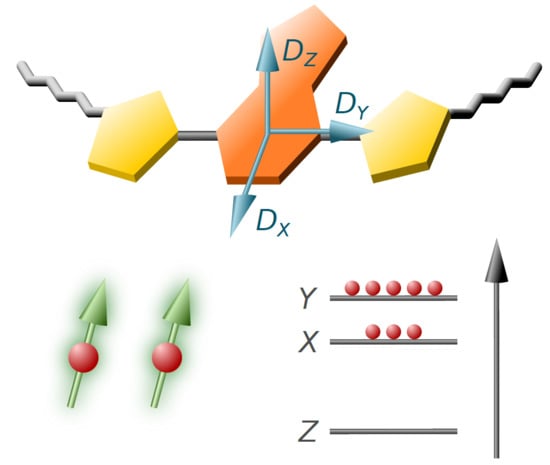
Impact of Side Chains of Conjugated Polymers on Electronic Structure: A Case Study
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Absorption Spectra
3.2. TREPR Spectra
3.3. DFT Calculations
4. Discussion
4.1. Acceptor Dominates Electronic Structure
4.2. Exciton Delocalization Extends with Backbone Length
4.3. Twisting the Backbone Reduces Curvature
4.4. Triplet Excitons Planarize the Polymer Backbone
4.5. Different Functionals/Basis Sets for Geometry Optimizations and Spin Density Calculations
4.6. D Tensor Calculations: Challenging But Informative
4.7. Four Distinct Factors Determining Exciton Delocalization
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A | Acceptor |
| Cbz | Carbazole |
| COSMO | Conductor-like Screening Model |
| CT | Charge Transfer |
| D | Donor |
| DFT | Density Functional Theory |
| ENDOR | Electron Nuclear Double Resonance |
| EPR | Electron Paramagnetic Resonance |
| ISC | Intersystem Crossing |
| PCDTBT | Poly[N-9-heptadecanyl-2,7-carbazole-alt-5,5-(4,7-di-2-thienyl-2,1,3-benzothiadiazole)] |
| PNDIT2 | Poly{[N,N-bis(2-octyldodecyl)-naphthalene-1,4,5,8-bis(dicarboximide)-2,6-diyl]-alt-5,5-(2,2-bithiophene)} |
| TBT | Dithienyl-Benzothiadiazole |
| TREPR | Time-Resolved Electron Paramagnetic Resonance |
| ZFS | Zero-Field Splitting |
References
- Forrest, S.R. The path to ubiquitious and low-cost organic electronic appliances on plastic. Nature 2004, 428, 911–918. [Google Scholar] [CrossRef]
- Katz, H.E.; Huang, J. Thin-film organic electronic devices. Ann. Rev. Mater. Res. 2009, 39, 71–92. [Google Scholar] [CrossRef]
- Sirringhaus, H. 25th anniversary article: Organic field-effect transistors: The path beyond amorphous silicon. Adv. Mater. 2014, 26, 1319–1335. [Google Scholar] [CrossRef]
- Lewis, J. Material challenge for flexible organic devices. Mater. Today 2006, 9, 38–45. [Google Scholar] [CrossRef]
- Logothetidis, S. Flexible organic electronic devices: Materials, process and applications. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 2008, 152, 96–104. [Google Scholar] [CrossRef]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and mechanics for stretchable electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef]
- Ling, H.; Liu, S.; Zheng, Z.; Yan, F. Organic flexible electronics. Small Meth. 2018, 2, 1800070. [Google Scholar] [CrossRef]
- Berggren, M.; Nilsson, D.; Robinson, N.D. Organic materials for printed electronics. Nat. Mater. 2007, 6, 3–5. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.; Lee, Y.; Cho, K.W.; Koo, J.H.; Kim, D.H. Wearable and implantable soft bioelectronics using two-dimensional materials. Acc. Chem. Res. 2019, 52, 73–81. [Google Scholar] [CrossRef]
- Wang, C.; Wang, C.; Huang, Z.; Xu, S. Materials and structures toward soft electronics. Adv. Mater. 2018, 30, 1801368. [Google Scholar] [CrossRef]
- Arias, A.C.; MacKenzie, J.D.; McCulloch, I.; Rivnay, J.; Salleo, A. Materials and applications for large area electronics: Solution-based approaches. Chem. Rev. 2010, 110, 3–24. [Google Scholar] [CrossRef]
- Xu, R.P.; Li, Y.Q.; Tang, J.X. Recent advances in flexible organic light-emitting diodes. J. Mater. Chem. C 2016, 4, 9116–9142. [Google Scholar] [CrossRef]
- Heeger, A.J. Semiconducting polymers: The Third Generation. Chem. Soc. Rev. 2010, 39, 2354–2371. [Google Scholar] [CrossRef]
- Darling, S.B.; You, F. The case for organic photovoltaics. RSC Adv. 2013, 3, 17633–17648. [Google Scholar] [CrossRef]
- Forrest, S.R. Excitons and the lifetime of organic semiconductor devices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140320. [Google Scholar] [CrossRef] [PubMed]
- Azzopardi, B.; Emmott, C.J.M.; Urbina, A.; Kresbs, F.C.; Mutale, J.; Nelson, J. Economic assessment of solar electricity production from organic-based photovoltaic modules in a domestic environment. Energy Environ. Sci. 2011, 4, 3741–3753. [Google Scholar] [CrossRef]
- Brabec, C.J.; Durrant, J.R. Solution-processed organic solar cells. MRS Bull. 2008, 33, 670–675. [Google Scholar] [CrossRef]
- Lu, L.; Zheng, T.; Wu, Q.; Schneider, A.M.; Zhao, D.; Yu, L. Recent advances in bulk heterojunction polymer solar cells. Chem. Rev. 2015, 115, 12666–12731. [Google Scholar] [CrossRef]
- Yeh, N.; Yeh, P. Organic solar cells: Their developments and potentials. Renew. Sust. Energ. Rev. 2013, 21, 421–431. [Google Scholar] [CrossRef]
- Sekine, C.; Tsubata, Y.; Yamada, T.; Kitano, M.; Doi, S. Recent progress of high performance polymer OLED and OPV materials for organic printed electronics. Sci. Technol. Adv. Mater. 2014, 15, 034203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faccetti, A. Seminconductors for organic transistors. Mater. Today 2007, 10, 28–37. [Google Scholar] [CrossRef]
- Janata, J.; Josowicz, M. Conducting polymers in electronic chemical sensors. Nat. Mater. 2002, 2, 19–24. [Google Scholar] [CrossRef] [PubMed]
- Jackson, N.E.; Savoie, B.M.; Marks, T.J.; Chen, L.X.; Ratner, M.A. The next breakthrough for organic photovoltaics? J. Phys. Chem. Lett. 2015, 6, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Scharber, M.C.; Mühlbacher, D.; Koppe, M.; Denk, P.; Waldauf, C.; Heeger, A.J.; Brabec, C.J. Design rules for donors in bulk-heterojunction solar cells—towards 10% energy-conversion efficiency. Adv. Mater. 2006, 18, 789–794. [Google Scholar] [CrossRef]
- Biskup, T. Structure–function relationship of organic semiconductors: Detailed insights from time-resolved EPR spectroscopy. Front. Chem. 2019, 7, 10. [Google Scholar] [CrossRef]
- Forbes, M.D.; Jarocha, L.E.; Sim, S.; Tarasov, V.F. Time-resolved electron paramagnetic resonance spectroscopy: History, technique, and application to supramolecular and macromolecular chemistry. Adv. Phys. Org. Chem. 2014, 47, 1–83. [Google Scholar]
- Weber, S. Transient EPR. eMagRes 2017, 6, 255–270. [Google Scholar]
- Biskup, T.; Sommer, M.; Rein, S.; Meyer, D.L.; Kohlstädt, M.; Würfel, U.; Weber, S. Ordering of PCDTBT revealed by time-resolved electron paramagnetic resonance spectroscopy of its triplet excitons. Angew. Chem. Int. Ed. 2015, 54, 7707–7710. [Google Scholar] [CrossRef]
- Meyer, D.L.; Matsidik, R.; Huettner, S.; Sommer, M.; Biskup, T. Solvent-mediated aggregate formation of PNDIT2: Decreasing the available conformational subspace by introducing locally highly ordered domains. Phys. Chem. Chem. Phys. 2018, 20, 2716–2723. [Google Scholar] [CrossRef]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudl, F.; Heeger, A.J. Polymer photovoltaic cells: Enhanced efficiencies via a network of internal donor-acceptor heterojunctions. Science 1995, 270, 1789–1791. [Google Scholar] [CrossRef]
- Szarko, J.M.; Guo, J.; Liang, Y.; Lee, B.; Rolczynski, B.S.; Strzalka, J.; Xu, T.; Loser, S.; Marks, T.J.; Yu, L.; et al. When function follows form: Effects of donor copolymer side chains on film morphology and BHJ solar cell performance. Adv. Mater. 2010, 22, 5468–5472. [Google Scholar] [CrossRef]
- Lan, S.C.; Chang, C.K.; Lu, Y.H.; Lin, S.W.; Jen, A.K.Y.; Wei, K.H. Side chain structure affects the molecular packing and photovoltaic performance of oligothiophene-based solution-processable small molecules. RSC Adv. 2015, 5, 67718–67726. [Google Scholar] [CrossRef]
- Oberhumer, P.M.; Huang, Y.S.; Massip, S.; James, D.T.; Tu, G.; Albert-Seifried, S.; Beljonne, D.; Cornil, J.; Kim, J.S.; Huck, W.T.S.; et al. Tuning the electronic coupling in a low-bandgap donor–acceptor copolymer via the placement of side-chains. J. Chem. Phys. 2011, 134, 114901. [Google Scholar] [CrossRef] [PubMed]
- Ko, S.; Hoke, E.T.; Pandey, L.; Hong, S.; Mondal, R.; Risko, C.; Yi, Y.; Noriega, R.; McGehee, M.D.; Brédas, J.L.; et al. Controlled conjugated backbone twisting for an increased open-circuit voltage while having a high short-circuit current in poly(hexylthiophene) derivatives. J. Am. Chem. Soc. 2012, 134, 5222–5232. [Google Scholar] [CrossRef]
- Lu, L.P.; Finlayson, C.E.; Kabra, D.; Albert-Seifried, S.; Song, M.H.; Havenith, R.W.A.; Tu, G.; Huck, W.T.S.; Friend, R.H. The influence of side-chain position on the optoelectronic properties of a red-emitting conjugated polymer. Macromol. Chem. Phys. 2013, 214, 967–974. [Google Scholar] [CrossRef]
- Mei, J.; Bao, Z. Side chain engineering in solution-processable conjugated polymers. Chem. Mater. 2014, 26, 604–615. [Google Scholar] [CrossRef]
- Banerji, N.; Gagnon, E.; Morgantini, P.Y.; Valouch, S.; Mohebbi, A.R.; Seo, J.H.; Leclerc, M.; Heeger, A.J. Breaking down the problem: Optical transitions, electronic structure, and photoconductivity in conjugated polymer PCDTBT and in its separate building blocks. J. Phys. Chem. C 2012, 116, 11456–11469. [Google Scholar] [CrossRef]
- Meyer, D.L.; Matsidik, R.; Sommer, M.; Biskup, T. Electronic structure trumps planarity: Unexpected narrow exciton delocalization in PNDIT2 revealed by time-resolved EPR spectroscopy. Adv. Electron. Mater. 2018, 4, 1700384. [Google Scholar] [CrossRef]
- Matt, C.; Meyer, D.L.; Lombeck, F.; Sommer, M.; Biskup, T. TBT entirely dominates the electronic structure of the conjugated copolymer PCDTBT: Insights from time-resolved electron paramagnetic resonance spectroscopy. Macromolecules 2018, 51, 4341–4349. [Google Scholar] [CrossRef]
- Blouin, N.; Michaud, A.; Leclerc, M. A low-bandgap poly(2,7-carbazole) derivative for use in high-performance solar cells. Adv. Mater. 2007, 19, 2295–2300. [Google Scholar] [CrossRef]
- Blouin, N.; Michaud, A.; Gendron, D.; Wakim, S.; Blair, E.; Neagu-Plesu, R.; Belletête, M.; Durocher, G.; Tao, Y.; Leclerc, M. Toward a rational design of poly(2,7-carbazole) derivatives for solar cells. J. Am. Chem. Soc. 2008, 130, 732–742. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, H.; Seifter, J.; Ying, L.; Mikhailovsky, A.; Heeger, A.J.; Bazan, G.C.; Nguyen, T.Q. Molecular doping enhances photoconductivity in polymer bulk heterojunction solar cells. Adv. Mater. 2013, 25, 7038–7044. [Google Scholar] [CrossRef]
- Cho, S.; Seo, J.H.; Park, S.H.; Beaupré, S.; Leclerc, M.; Heeger, A.J. A thermally stable semiconducting polymer. Adv. Mater. 2010, 22, 1253–1257. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Takacs, C.J.; Cowan, S.R.; Seo, J.H.; Gong, X.; Roy, A.; Heeger, A.J. Efficient, air-stable bulk heterojunction polymer solar cells using MoOx as the anode interfacial layer. Adv. Mater. 2011, 23, 2226–2230. [Google Scholar] [CrossRef]
- Peters, C.H.; Sachs-Quintana, I.T.; Kastrop, J.P.; Beaupré, S.; Leclerc, M.; McGehee, M.D. High efficiency polymer solar cells with long operating lifetimes. Adv. Energy Mater. 2011, 1, 491–494. [Google Scholar] [CrossRef]
- Kong, J.; Song, S.; Yoo, M.; Lee, G.Y.; Kwon, O.; Park, J.K.; Back, H.; Kim, G.; Lee, S.H.; Suh, H.; et al. Long-term stable polymer solar cells with significantly reduced burn-in loss. Nat. Commun. 2014, 5, 5688. [Google Scholar] [CrossRef] [Green Version]
- Beaupré, S.; Leclerc, M. PCDTBT: en route for low cost plastic solar cells. J. Mater. Chem. A 2013, 1, 11097–11105. [Google Scholar] [CrossRef]
- Lombeck, F.; Komber, H.; Fazzi, D.; Nava, D.; Kuhlmann, J.; Stegerer, D.; Strassel, K.; Brandt, J.; de Zerio Mendaza, A.D.; Müller, C.; et al. On the effect of prevalent carbazole homocoupling defects on the photovoltaic performance of PCDTBT:PC71BM solar cells. Adv. Energy Mater. 2016, 6, 1601232. [Google Scholar] [CrossRef]
- Beiley, Z.M.; Hoke, E.T.; Noriega, R.; Dacuña, J.; Burkhard, G.F.; Bartelt, J.A.; Salleo, A.; Toney, M.F.; McGehee, M.D. Morphology-dependent trap formation in high performance polymer bulk heterojunction solar cells. Adv. Energy Mater. 2011, 1, 954–962. [Google Scholar] [CrossRef]
- Wang, H.W.; Pentzer, E.; Emrick, T.; Russell, T.P. Preparation of low band gap fibrillar structures by solvent-induced crystallization. ACS Macro Lett. 2014, 3, 30–34. [Google Scholar] [CrossRef]
- Ibraikulov, O.A.; Ngov, C.; Chávez, P.; Bulut, I.; Heinrich, B.; Boyron, O.; Ivanov, K.L.G.D.A.; Swaraj, S.; Méry, S.; Leclerc, N.; et al. Face-on orientation of fluorinated polymers conveyed by long alkyl chains: A prerequisite for high photovoltaic performances. J. Mater. Chem. A 2018, 6, 12038–12045. [Google Scholar] [CrossRef]
- Osaka, I.; Kakara, T.; Takemura, N.; Koganezawa, T.; Takimiya, K. Naphthodithiophene–naphthobisthiadiazole copolymers for solar cells: Alkylation drives the polymer backbone flat and promotes efficiency. J. Am. Chem. Soc. 2015, 135, 8834–8837. [Google Scholar] [CrossRef] [PubMed]
- Rand, B.P.; Cheyns, D.; Vasseur, K.; Giebink, N.C.; Mothy, S.; Yi, Y.; Coropceanu, V.; Beljonne, D.; Cornil, J.; Brédas, J.L.; et al. The impact of molecular orientation on the photovoltaic properties of a phthalocyanine/fullerene heterojunction. Adv. Funct. Mater. 2012, 22, 2987–2995. [Google Scholar] [CrossRef]
- Akaike, K.; Ando, S.; Enozawa, H.; Kosaka, A.; Kajitani, T.; Fukushima, T. An electron-accepting molecular unit exhibiting an orientational preference favorable for organic photovoltaic applications. Thin Solid Film. 2015, 583, 34–39. [Google Scholar] [CrossRef]
- Meyer, D.L.; Schmidt-Meinzer, N.; Rein, S.; Matt, C.; Lombeck, F.; Sommer, M.; Biskup, T. Side-chain engineering of conjugated polymers: Distinguishing its impact on film morphology and electronic structure. J. Phys. Chem. C 2019, submitted. [Google Scholar]
- Lombeck, F.; Di, D.; Yang, L.; Meraldi, L.; Athanasopoulos, S.; Credgington, D.; Sommer, M.; Friend, R.H. PCDTBT: From polymer photovoltaics to light-emitting diodes by side-chain-controlled luminescence. Macromolecules 2016, 49, 9382–9387. [Google Scholar] [CrossRef]
- Lombeck, F.; Komber, H.; Gorelsky, S.I.; Sommer, M. Identifying homocouplings as critical side reactions in direct arylation polycondensation. ACS Macro Lett. 2014, 3, 819–823. [Google Scholar] [CrossRef]
- Meyer, D.L.; Lombeck, F.; Huettner, S.; Sommer, M.; Biskup, T. Direct S0→T excitation of a conjugated polymer repeat unit: Unusual spin-forbidden transitions probed by time-resolved electron paramagnetic resonance spectroscopy. J. Phys. Chem. Lett. 2017, 8, 1677–1682. [Google Scholar] [CrossRef]
- Lombeck, F.; Marx, F.; Strassel, K.; Kunz, S.; Lienert, C.; Komber, H.; Friend, R.; Sommer, M. To branch or not to branch: C–H selectivity of thiophene-based donor–acceptor–donor monomers in direct arylation polycondensation exemplified by PCDTBT. Polym. Chem. 2017, 8, 4738–4745. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef] [Green Version]
- Neese, F. The ORCA program package. Wiley Interdiscip. Rev.-Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Becke, A.D. Density–functional exchange–energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density–functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Al-Laham, M.A.; Shirley, W.A.; Mantzaris, J. A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row elements. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Petersson, G.A.; Al-Laham, M.A. A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms. J. Chem. Phys. 1991, 94, 6081–6090. [Google Scholar] [CrossRef]
- Barone, V. Structure, Magnetic Properties and Reactivities of Open-Shell Species From Density Functional and Self-Consistent Hybrid Methods. In Recent Advances in Density Functional Methods (Part I); Recent Advances in Computational Chemistry; Chong, D.P., Ed.; World Scientific: Singapore, 1995; Volume 1, Chapter 8; pp. 287–334. [Google Scholar]
- Sinnecker, S.; Rajendran, A.; Klamt, A.; Diedenhofen, M.; Neese, F. Calculation of solvent shifts on electronic g-tensors with the conductor-like screening model (COSMO) and its self-consistent generalization to real solvents (direct COSMO-RS). J. Phys. Chem. A 2006, 110, 2235–2245. [Google Scholar] [CrossRef] [PubMed]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Biskup, T. Time-resolved EPR of radical pair intermediates in cryptochromes. Mol. Phys. 2013, 111, 3698–3703. [Google Scholar] [CrossRef]
- Hall, P.L.; Angel, B.R.; Jones, J.P.E. Dependence of spin Hamiltonian parameters E and D on labeling of magnetic axes: Application to ESR of high-spin Fe3+. J. Magn. Reson. 1974, 15, 64–68. [Google Scholar] [CrossRef]
- Weil, J.A.; Bolton, J.R. Electron Paramagnetic Resonance: Elementary Theory and Practical Applications, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Franco, F., Jr. Computational study on the structural and optoelectronic properties of a cabazole-benzothiadiazole based conjugated oligomer with various alkyl side-chain lengths. Mol. Simul. 2017, 43, 222–227. [Google Scholar] [CrossRef]
- Akimov, A.; Masitov, A.; Korchagin, D.; Chapyshev, S.; Misochko, E.; Savitsky, A. W-band EPR studies of high-spin nitrenes with large spin-orbit contribution to zero-field splitting. J. Chem. Phys. 2015, 143, 084313. [Google Scholar] [CrossRef] [PubMed]
- Risko, C.; McGehee, M.D.; Brédas, J.L. A quantum-chemical perspective into low optical-bandgap polymers for highly-efficient organic solar cells. Chem. Sci. 2011, 2, 1200–1218. [Google Scholar] [CrossRef]
- Hornig, A.W.; Hyde, J.S. Paramagnetic resonance in triplet naphthalene at liquid helium temperatures. Mol. Phys. 1963, 6, 33–41. [Google Scholar] [CrossRef]
- Schuch, H.; Seiff, F.; Furrer, R.; Möbius, K.; Dinse, K.P. Direkte Bestimmung des absoluten Vorzeichens des Triplett-Nullfeld-Parameters D mit hochauflösender optischer Detektion von ESR. Z. Naturforsch. A 1974, 29, 1543–1547. [Google Scholar] [CrossRef]
- Hochstrasser, R.M.; Lin, T.S. Magnetic and electric field spectra of organic crystals: Optical measurements of zero-field splittings. J. Chem. Phys. 1968, 49, 4929–4945. [Google Scholar] [CrossRef]
- Tinti, D.S.; Kothandaraman, G.; Harris, C.B. Determination of the absolute sign of the electron spin dipolar and nuclear quadrupolar interactions in molecular excited triplet states. J. Chem. Phys. 1973, 59, 190–193. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sakamoto, N. Exchange interactions and magnetic susceptibilities of Ni2+ in KMgF3 and K2MgF4. J. Phys. Soc. Jpn. 1969, 27, 1444–1450. [Google Scholar] [CrossRef]
- Tait, C.E.; Neuhaus, P.; Anderson, H.L.; Timmel, C.R. Triplet state delocalization in a conjugated porphyrin dimer probed by transient electron paramagnetic resonance techniques. J. Am. Chem. Soc. 2015, 137, 6670–6679. [Google Scholar] [CrossRef] [PubMed]











| Compound | (nm) | (MHz) | (MHz) | (mT) | ||
|---|---|---|---|---|---|---|
| A | 466 | |||||
| D-A | 490 | |||||
| D-A-D | 509 | |||||
| (D-A)n | 518 |
| Compound | State | Dihedral Angles | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D-A | singlet | 35.4 | |||||||||||||
| triplet | 27.0 | ||||||||||||||
| D-A-D | singlet | 37.2 | 35.8 | ||||||||||||
| triplet | 28.7 | 27.0 | |||||||||||||
| (D-A)4 | singlet | 36.2 | 31.7 | 39.3 | 34.3 | 35.2 | 35.1 | 35.4 | |||||||
| triplet | 36.6 | 34.3 | 38.1 | 30.3 | 22.5 | 25.2 | 34.0 | ||||||||
| (D-A)7-D | singlet | 38.2 | 37.3 | 38.7 | 36.0 | 41.3 | 32.5 | 36.4 | 32.9 | 33.4 | 33.0 | 38.2 | 38.3 | 35.2 | 34.9 |
| triplet | 39.3 | 34.7 | 36.5 | 31.8 | 23.3 | 24.5 | 32.4 | 36.5 | 43.2 | 39.3 | 35.7 | 34.7 | 35.5 | 36.1 | |
| Compound | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Calculated | Experimental | |||||||||
| A | 808 | 179 | 0.22 | 1539 | 88 | 0.06 | 0.0 | 0.0 | 0.0 | 1.00 |
| D-A | 736 | 173 | 0.24 | 1457 | 91 | 0.06 | 2.3 | 2.3 | 0.2 | 0.92 |
| D-A-D | 688 | 170 | 0.25 | 1387 | 96 | 0.07 | 0.1 | 0.2 | 0.2 | 0.88 |
| (D-A)n | 675 | 173 | 0.26 | 1384 | 87 | 0.06 | 0.2 | 0.0 | 0.2 | 0.85 |
| Compound | (MHz) | (MHz) | ||||
|---|---|---|---|---|---|---|
| A | ||||||
| D-A | ||||||
| D-A-D | ||||||
| (D-A)n |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matt, C.; Lombeck, F.; Sommer, M.; Biskup, T. Impact of Side Chains of Conjugated Polymers on Electronic Structure: A Case Study. Polymers 2019, 11, 870. https://doi.org/10.3390/polym11050870
Matt C, Lombeck F, Sommer M, Biskup T. Impact of Side Chains of Conjugated Polymers on Electronic Structure: A Case Study. Polymers. 2019; 11(5):870. https://doi.org/10.3390/polym11050870
Chicago/Turabian StyleMatt, Clemens, Florian Lombeck, Michael Sommer, and Till Biskup. 2019. "Impact of Side Chains of Conjugated Polymers on Electronic Structure: A Case Study" Polymers 11, no. 5: 870. https://doi.org/10.3390/polym11050870
APA StyleMatt, C., Lombeck, F., Sommer, M., & Biskup, T. (2019). Impact of Side Chains of Conjugated Polymers on Electronic Structure: A Case Study. Polymers, 11(5), 870. https://doi.org/10.3390/polym11050870