Development of Expanded Takayanagi Model for Tensile Modulus of Carbon Nanotubes Reinforced Nanocomposites Assuming Interphase Regions Surrounding the Dispersed and Networked Nanoparticles
Abstract
:1. Introduction
2. Equations
3. Results and Discussion
3.1. Evaluation of Model by Experimental Data
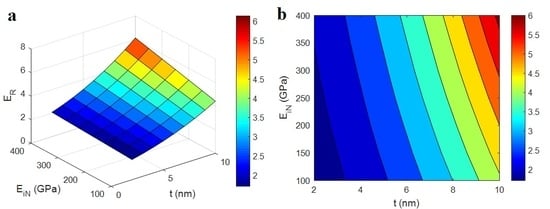
3.2. Parametric Analyses
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, C.F.; Wang, W.N.; Lin, C.H.; Lee, K.J.; Hu, C.C.; Lai, J.Y. Facile Fabrication of Durable Superhydrophobic Films from Carbon Nanotube/Main-Chain Type Polybenzoxazine Composites. Polymers 2019, 11, 1183. [Google Scholar] [CrossRef] [Green Version]
- Keshtkar, M.; Mehdipour, N.; Eslami, H. Thermal Conductivity of Polyamide-6, 6/Carbon Nanotube Composites: Effects of Tube Diameter and Polymer Linkage between Tubes. Polymers 2019, 11, 1465. [Google Scholar] [CrossRef] [Green Version]
- Shokri-Oojghaz, R.; Moradi-Dastjerdi, R.; Mohammadi, H.; Behdinan, K. Stress distributions in nanocomposite sandwich cylinders reinforced by aggregated carbon nanotube. Polym. Compos. 2019, 40, E1918–E1927. [Google Scholar] [CrossRef]
- Liu, S.; Wu, G.; Chen, X.; Zhang, X.; Yu, J.; Liu, M.; Zhang, Y.; Wang, P. Degradation Behavior In Vitro of Carbon Nanotubes (CNTs)/Poly (lactic acid)(PLA) Composite Suture. Polymers 2019, 11, 1015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, G.; Gu, Y.; Hou, X.; Li, R.; Ke, H.; Xiao, X. Hybrid Nanocomposites of Cellulose/Carbon-Nanotubes/Polyurethane with Rapidly Water Sensitive Shape Memory Effect and Strain Sensing Performance. Polymers 2019, 11, 1586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Cao, C.; Chen, X.; Ren, S.; Chen, Y.; Yu, D.; Chen, X. Orientation and Dispersion Evolution of Carbon Nanotubes in Ultra High Molecular Weight Polyethylene Composites under Extensional-Shear Coupled Flow: A Dissipative Particle Dynamics Study. Polymers 2019, 11, 154. [Google Scholar] [CrossRef] [Green Version]
- Bakhtiari, S.S.E.; Karbasi, S.; Tabrizi, S.A.H.; Ebrahimi-Kahrizsangi, R. Chitosan/MWCNTs composite as bone substitute: Physical, mechanical, bioactivity, and biodegradation evaluation. Polym. Compos. 2019, 40, E1622–E1632. [Google Scholar] [CrossRef]
- Rostami, A.; Vahdati, M.; Nazockdast, H. Unraveling the localization behavior of MWCNTs in binary polymer blends using thermodynamics and viscoelastic approaches. Polym. Compos. 2018, 39, 2356–2367. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Liu, B. Carbon Nanotube-Based Organic Thermoelectric Materials for Energy Harvesting. Polymers 2018, 10, 1196. [Google Scholar] [CrossRef] [Green Version]
- Zagho, M.; AlMaadeed, M.; Majeed, K. Thermal properties of TiO2NP/CNT/LDPE hybrid nanocomposite films. Polymers 2018, 10, 1270. [Google Scholar] [CrossRef] [Green Version]
- Zare, Y.; Rhee, K.Y. Modeling of viscosity and complex modulus for poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanocomposites assuming yield stress and network breaking time. Compos. Part B Eng. 2019, 156, 100–107. [Google Scholar] [CrossRef]
- Zare, Y.; Park, S.P.; Rhee, K.Y. Analysis of complex viscosity and shear thinning behavior in poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes biosensor based on Carreau–Yasuda model. Results Phys. 2019, 13, 102245. [Google Scholar] [CrossRef]
- Tang, Z.; Jia, S.; Shi, X.; Li, B.; Zhou, C. Coaxial Printing of Silicone Elastomer Composite Fibers for Stretchable and Wearable Piezoresistive Sensors. Polymers 2019, 11, 666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yue, Y.; Wang, X.; Wu, Q.; Han, J.; Jiang, J. Assembly of Polyacrylamide-Sodium Alginate-Based Organic-Inorganic Hydrogel with Mechanical and Adsorption Properties. Polymers 2019, 11, 1239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otaegi, I.; Aranburu, N.; Iturrondobeitia, M.; Ibarretxe, J.; Guerrica-Echevarría, G. The Effect of the Preparation Method and the Dispersion and Aspect Ratio of CNTs on the Mechanical and Electrical Properties of Bio-Based Polyamide-4, 10/CNT Nanocomposites. Polymers 2019, 11, 2059. [Google Scholar] [CrossRef] [Green Version]
- Zare, Y.; Rhee, K.Y. Following the morphological and thermal properties of PLA/PEO blends containing carbon nanotubes (CNTs) during hydrolytic degradation. Compos. Part B Eng. 2019, 175, 107132. [Google Scholar] [CrossRef]
- Zou, W.; Du, Z.J.; Liu, Y.X.; Yang, X.; Li, H.Q.; Zhang, C. Functionalization of MWNTs using polyacryloyl chloride and the properties of CNT–epoxy matrix nanocomposites. Compos. Sci. Technol. 2008, 68, 3259–3264. [Google Scholar] [CrossRef]
- Kim, S.; Zare, Y.; Garmabi, H.; Rhee, K.Y. Variations of tunneling properties in poly (lactic acid)(PLA)/poly (ethylene oxide)(PEO)/carbon nanotubes (CNT) nanocomposites during hydrolytic degradation. Sens. Actuators A Phys. 2018, 274, 28–36. [Google Scholar] [CrossRef]
- Park, J.M.; Gu, G.Y.; Wang, Z.J.; Kwon, D.J.; DeVries, K.L. Interfacial durability and electrical properties of CNT or ITO/PVDF nanocomposites for self-sensor and micro actuator applications. Appl. Surf. Sci. 2013, 287, 75–83. [Google Scholar] [CrossRef]
- Rostami, A.; Moosavi, M.I. High-performance thermoplastic polyurethane nanocomposites induced by hybrid application of functionalized graphene and carbon nanotubes. J. Appl. Polym. Sci. 2019, 48520. [Google Scholar] [CrossRef]
- Jeong, W.; Kessler, M.R. Effect of functionalized MWCNTs on the thermo-mechanical properties of poly (5-ethylidene-2-norbornene) composites produced by ring-opening metathesis polymerization. Carbon 2009, 47, 2406–2412. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Evaluation of the Tensile Strength in Carbon Nanotube-Reinforced Nanocomposites Using the Expanded Takayanagi Model. JOM 2019, 71, 1–9. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y.; Park, S.J. Modeling the roles of carbon nanotubes and interphase dimensions in the conductivity of nanocomposites. Results Phys. 2019, 15, 102562. [Google Scholar] [CrossRef]
- Rostami, A.; Eskandari, F.; Masoomi, M.; Nowrouzi, M. Evolution of Microstructure and Physical Properties of PMMA/MWCNTs Nanocomposites upon the Addition of Organoclay. J. Oil Gas Petrochem. Technol. 2019, 6, 28–38. [Google Scholar]
- Zare, Y.; Rhee, K.Y. The effective conductivity of polymer carbon nanotubes (CNT) nanocomposites. J. Phys. Chem. Solids 2019, 131, 15–21. [Google Scholar] [CrossRef]
- Bartczak, Z.; Argon, A.; Cohen, R.; Weinberg, M. Toughness mechanism in semi-crystalline polymer blends: II. High-density polyethylene toughened with calcium carbonate filler particles. Polymer 1999, 40, 2347–2365. [Google Scholar] [CrossRef]
- Favier, V.; Cavaille, J.; Canova, G.; Shrivastava, S. Mechanical percolation in cellulose whisker nanocomposites. Polym. Eng. Sci. 1997, 37, 1732–1739. [Google Scholar] [CrossRef]
- Favier, V.; Chanzy, H.; Cavaille, J. Polymer nanocomposites reinforced by cellulose whiskers. Macromolecules 1995, 28, 6365–6367. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K. Evaluation and Development of Expanded Equations Based on Takayanagi Model for Tensile Modulus of Polymer Nanocomposites Assuming the Formation of Percolating Networks. Phys. Mesomech. 2018, 21, 351–357. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y.; Park, S.J. A modeling methodology to investigate the effect of interfacial adhesion on the yield strength of MMT reinforced nanocomposites. J. Ind. Eng. Chem. 2019, 69, 331–337. [Google Scholar] [CrossRef]
- Peng, W.; Rhim, S.; Zare, Y.; Rhee, K.Y. Effect of “Z” factor for strength of interphase layers on the tensile strength of polymer nanocomposites. Polym. Compos. 2019, 40, 1117–1122. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Effects of interphase regions and filler networks on the viscosity of PLA/PEO/carbon nanotubes biosensor. Polym. Compos. 2019, 40, 4135–4141. [Google Scholar] [CrossRef]
- Hassanzadeh-Aghdam, M.K.; Mahmoodi, M.J.; Ansari, R. Creep performance of CNT polymer nanocomposites-An emphasis on viscoelastic interphase and CNT agglomeration. Compos. Part B Eng. 2019, 168, 274–281. [Google Scholar] [CrossRef]
- Zare, Y.; Rhim, S.; Garmabi, H.; Rhee, K.Y. A simple model for constant storage modulus of poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanocomposites at low frequencies assuming the properties of interphase regions and networks. J. Mech. Behav. Biomed. Mater. 2018, 80, 164–170. [Google Scholar] [CrossRef] [PubMed]
- Zare, Y.; Rhee, K.Y. Tensile strength prediction of carbon nanotube reinforced composites by expansion of cross-orthogonal skeleton structure. Compos. Part B Eng. 2019, 161, 601–607. [Google Scholar] [CrossRef]
- Baxter, S.C.; Robinson, C.T. Pseudo-percolation: Critical volume fractions and mechanical percolation in polymer nanocomposites. Compos. Sci. Technol. 2011, 71, 1273–1279. [Google Scholar] [CrossRef]
- Shin, H.; Yang, S.; Choi, J.; Chang, S.; Cho, M. Effect of interphase percolation on mechanical behavior of nanoparticle-reinforced polymer nanocomposite with filler agglomeration: A multiscale approach. Chem. Phys. Lett. 2015, 635, 80–85. [Google Scholar] [CrossRef]
- Celzard, A.; McRae, E.; Deleuze, C.; Dufort, M.; Furdin, G.; Marêché, J. Critical concentration in percolating systems containing a high-aspect-ratio filler. Phys. Rev. B 1996, 53, 6209. [Google Scholar] [CrossRef]
- Loos, M.; Manas-Zloczower, I. Micromechanical models for carbon nanotube and cellulose nanowhisker reinforced composites. Polym. Eng. Sci. 2013, 53, 882–887. [Google Scholar] [CrossRef]
- Razavi, R.; Zare, Y.; Rhee, K.Y. The roles of interphase and filler dimensions in the properties of tunneling spaces between CNT in polymer nanocomposites. Polym. Compos. 2019, 40, 801–810. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y.; Park, S.J. A developed equation for electrical conductivity of polymer carbon nanotubes (CNT) nanocomposites based on Halpin-Tsai model. Results Phys. 2019, 14, 102406. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.W. Carbon nanotube networks: Sensing of distributed strain and damage for life prediction and self healing. Adv. Mater. 2006, 18, 2837–2841. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, S.; Wang, F.; Wen, B.; Han, C.; Ding, Y.; Yang, M. Graphene networks with low percolation threshold in ABS nanocomposites: Selective localization and electrical and rheological properties. ACS Appl. Mater. Interfaces 2014, 6, 12252–12260. [Google Scholar] [CrossRef] [PubMed]
- Du, F.; Scogna, R.C.; Zhou, W.; Brand, S.; Fischer, J.E.; Winey, K.I. Nanotube networks in polymer nanocomposites: Rheology and electrical conductivity. Macromolecules 2004, 37, 9048–9055. [Google Scholar] [CrossRef]
- Cao, X.; Dong, H.; Li, C.M.; Lucia, L.A. The enhanced mechanical properties of a covalently bound chitosan-multiwalled carbon nanotube nanocomposite. J. Appl. Polym. Sci. 2009, 113, 466–472. [Google Scholar] [CrossRef]
- Yang, B.X.; Shi, J.H.; Pramoda, K.; Goh, S.H. Enhancement of the mechanical properties of polypropylene using polypropylene-grafted multiwalled carbon nanotubes. Compos. Sci. Technol. 2008, 68, 2490–2497. [Google Scholar] [CrossRef]
- Mi, Y.; Zhang, X.; Zhou, S.; Cheng, J.; Liu, F.; Zhu, H.; Dong, X.; Jiao, Z. Morphological and mechanical properties of bile salt modified multi-walled carbon nanotube/poly (vinyl alcohol) nanocomposites. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2041–2046. [Google Scholar] [CrossRef]
- Chen, S.; Sarafbidabad, M.; Zare, Y.; Rhee, K.Y. Estimation of the tensile modulus of polymer carbon nanotube nanocomposites containing filler networks and interphase regions by development of the Kolarik model. RSC Adv. 2018, 8, 23825–23834. [Google Scholar] [CrossRef] [Green Version]
- Al-Saleh, M.H. Influence of conductive network structure on the EMI shielding and electrical percolation of carbon nanotube/polymer nanocomposites. Synth. Met. 2015, 205, 78–84. [Google Scholar] [CrossRef]
- Chatterjee, A.P. A model for the elastic moduli of three-dimensional fiber networks and nanocomposites. J. Appl. Phys. 2006, 100, 054302. [Google Scholar] [CrossRef]
- Zhou, Z.; Sarafbidabad, M.; Zare, Y.; Rhee, K.Y. Prediction of storage modulus in solid-like poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes nanocomposites assuming the contributions of nanoparticles and interphase regions in the networks. J. Mech. Behav. Biomed. Mater. 2018, 86, 368–374. [Google Scholar] [CrossRef] [PubMed]
- Wan, C.; Chen, B. Reinforcement and interphase of polymer/graphene oxide nanocomposites. J. Mater. Chem. 2012, 22, 3637–3646. [Google Scholar] [CrossRef]
- Rafiee, R.; Pourazizi, R. Influence of CNT functionalization on the interphase region between CNT and polymer. Comput. Mater. Sci. 2014, 96, 573–578. [Google Scholar] [CrossRef]
- Choi, J.; Shin, H.; Yang, S.; Cho, M. The influence of nanoparticle size on the mechanical properties of polymer nanocomposites and the associated interphase region: A multiscale approach. Compos. Struct. 2015, 119, 365–376. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. A Simulation Work for the Influences of Aggregation/Agglomeration of Clay Layers on the Tensile Properties of Nanocomposites. JOM 2019, 71, 3989–3995. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. A multistep methodology for calculation of the tensile modulus in polymer/carbon nanotube nanocomposites above the percolation threshold based on the modified rule of mixtures. RSC Adv. 2018, 8, 30986–30993. [Google Scholar] [CrossRef] [Green Version]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, Y.; Rhee, K.Y. Development of Expanded Takayanagi Model for Tensile Modulus of Carbon Nanotubes Reinforced Nanocomposites Assuming Interphase Regions Surrounding the Dispersed and Networked Nanoparticles. Polymers 2020, 12, 233. https://doi.org/10.3390/polym12010233
Zare Y, Rhee KY. Development of Expanded Takayanagi Model for Tensile Modulus of Carbon Nanotubes Reinforced Nanocomposites Assuming Interphase Regions Surrounding the Dispersed and Networked Nanoparticles. Polymers. 2020; 12(1):233. https://doi.org/10.3390/polym12010233
Chicago/Turabian StyleZare, Yasser, and Kyong Yop Rhee. 2020. "Development of Expanded Takayanagi Model for Tensile Modulus of Carbon Nanotubes Reinforced Nanocomposites Assuming Interphase Regions Surrounding the Dispersed and Networked Nanoparticles" Polymers 12, no. 1: 233. https://doi.org/10.3390/polym12010233
APA StyleZare, Y., & Rhee, K. Y. (2020). Development of Expanded Takayanagi Model for Tensile Modulus of Carbon Nanotubes Reinforced Nanocomposites Assuming Interphase Regions Surrounding the Dispersed and Networked Nanoparticles. Polymers, 12(1), 233. https://doi.org/10.3390/polym12010233