Thermodynamic and Transport Properties of Tetrabutylphosphonium Hydroxide and Tetrabutylphosphonium Chloride–Water Mixtures via Molecular Dynamics Simulation †
Abstract
:1. Introduction
2. Methodology
3. Results
3.1. Force Field Validation: TBPH–Water and TBPCl–Water Densities
3.2. Structural Properties
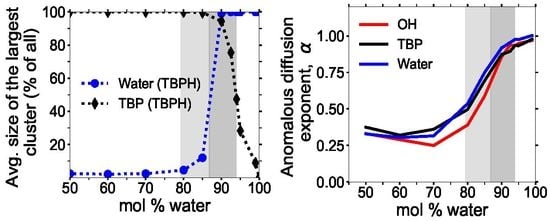
3.3. Clustering of Water and TBP
3.4. Hydrogen Bonding
3.5. Thermodynamic Data
3.5.1. Excess Properties
3.5.2. Heat Capacity and Thermal Expansivity
3.6. Diffusion Properties
3.7. Comparison between Aqueous Solutions of Alkylimidazolium ILs and TBPH
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AMBER | Assisted model building with energy refinement |
| BMIM | 1-butyl-3-methylimidazolium |
| Cl | Chloride |
| DMF | Dimethylformamide |
| EMIM | 1-ethyl-3-methylimidazolium |
| GLYCAM06 | Glycosylation-dependent cell adhesion molecule 2006 |
| IL | Ionic Liquid |
| LAMMPS | Large-scale atomic/molecular massively parallel simulator |
| LJ | Lennard-Jones |
| MD | Molecular dynamics |
| MSD | Mean squared displacement |
| MSDS | Material safety data sheet |
| NPT | Isobaric-isothermal |
| NVT | Constant volume-isothermal |
| O | Oxygen |
| OH | Hydroxide |
| P | Phosphorous |
| PPPM | Particle–particle–particle–mesh |
| ReaxFF | Type of reactive force field |
| RESPA | Reversible reference system propagator algorithms |
| TAMSD | Time-averaged mean squared displacement |
| TBA | Tetrabutylammonium |
| TBACl | Tetrabutylammonium chloride |
| TBAH | Tetrabutylammonium hydroxide |
| TBP | Tetrabutylphosphonium |
| TBPCl | Tetrabutylphosphonium chloride |
| TBPH | Tetrabutylphosphonium hydroxide |
| TIP3P | Three-site transferrable intermolecular potential |
| TIP4P | Four-site transferrable intermolecular potential |
| VMD | Visual molecular dynamics |
| Etotal | Total potential energy |
| Kr | Potential energy bond constant |
| Kθ | Potential energy angle constant |
| Kϕ | Potential energy torsion/dihedral angle constant |
| n | Number of maximums in the torsion/dihedral angle |
| qi | Charge of atom i |
| qj | Charge of atom j |
| r | Bond length |
| rij | Radial distance between atoms i and j |
| r0 | Equilibrium bond length |
| γ | Equilibrium torsion/dihedral angle |
| ϵij | Well depth of LJ potential between atoms i and j |
| θ | Bond angle |
| θ0 | Equilibrium bond angle |
| σij | Zero of LJ potential between atoms i and j |
| ϕ | Torsion/dihedral angle |
| t | Time |
| Δ | Lag time |
| ri | Center of mass of molecule i |
| Mean squared displacement (MSD) | |
| Time-averaged mean squared displacement (TAMSD) of molecule i | |
| Particle-averaged TAMSD | |
| Kα | Generalized diffusion coefficient |
| α | Anomalous diffusion exponent |
| χ | Ergodicity breaking parameter |
| cp | Heat capacity at constant pressure |
| αp | Thermal expansivity at constant pressure |
Appendix A
Appendix A.1. RDFs at Varying Water Concentrations for TBPCl


Appendix A.2. Simulation Snapshots at Varying Water Concentrations for TBPCl




Appendix A.3. Diffusion Properties


| Kα (10−6 cm2 s−1)/α (1/sα) | ||||||
|---|---|---|---|---|---|---|
| H2O | TBP+ | Cl− | ||||
| Mole% | Kα | α | Kα | α | Kα | α |
| 50.0 | 0.660 | 0.314 | 0.208 | 0.394 | 0.483 | 0.321 |
| 60.0 | 0.796 | 0.379 | 0.214 | 0.309 | 0.527 | 0.282 |
| 70.0 | 1.27 | 0.506 | 0.226 | 0.409 | 0.520 | 0.348 |
| 80.0 | 2.2 | 0.664 | 0.341 | 0.494 | 0.674 | 0.500 |
| 85.0 | 3.79 | 0.818 | 0.520 | 0.747 | 0.909 | 0.699 |
| 90.0 | 8.61 | 0.923 | 1.11 | 0.871 | 2.42 | 0.847 |
| 92.5 | 12.6 | 0.974 | 1.80 | 0.922 | 4.16 | 0.916 |
| 94.0 | 19.2 | 0.968 | 2.71 | 0.901 | 6.79 | 0.947 |
| 95.0 | 23.3 | 0.981 | 3.21 | 0.960 | 9.02 | 0.935 |
| 99.0 | 89.3 | 0.986 | 14.3 | 0.982 | 41.8 | 1.05 |
| 99.97 a | 141 | 0.991 | – – | – – | – – | – – |



References
- Fang, Z.; Smith, R.L.; Qi, X. (Eds.) Production of Biofuels and Chemicals with Ionic Liquids; Springer: Dordrecht, The Netherlands, 2014; pp. 1–340. [Google Scholar]
- Abe, H. Fast and facile dissolution of cellulose with tetrabutylphosphonium hydroxide containing 40 wt% water. Chem. Commun. 2012, 48, 11808–11810. [Google Scholar] [CrossRef] [PubMed]
- Burns, F.P. Assessment of phosphonium ionic liquid-dimethylformamide mixtures for dissolution of cellulose. Compos. Interfaces 2013, 21, 59–73. [Google Scholar] [CrossRef]
- Rabideau, B.D. Observed Mechanism for the Breakup of Small Bundles of Cellulose Iα and Iβ in Ionic Liquids from Molecular Dynamics Simulations. J. Phys. Chem. B 2013, 117, 3469–3479. [Google Scholar] [CrossRef] [PubMed]
- Mazza, M. Influence of water on the dissolution of cellulose in selected ionic liquids. Cellulose 2009, 16, 207–215. [Google Scholar] [CrossRef]
- Swatloski, R. Dissolution of Cellulose with Ionic Liquids. J. Am. Chem. Soc. 2002, 124, 4974–4975. [Google Scholar] [CrossRef] [PubMed]
- Viell, J. Disintegration and dissolution kinetics of wood chips in ionic liquids. Holzforschung 2011, 65, 519–525. [Google Scholar] [CrossRef]
- Viell, J. Multi-scale processes of beech wood disintegration and pretreatment with 1-ethyl-3-methylimidazolium acetate/water mixtures. Biotechnol. Biofuels 2016, 9, 7. [Google Scholar] [CrossRef] [Green Version]
- Parthasarathi, R. Theoretical Insights into the Role of Water in the Dissolution of Cellulose Using IL/Water Mixed Solvent Systems. J. Phys. Chem. B 2015, 119, 14339–14349. [Google Scholar] [CrossRef]
- Niazi, A.A. Effects of Water Concentration on the Structural and Diffusion Properties of Imidazolium-Based Ionic Liquid–Water Mixtures. J. Phys. Chem. B 2013, 117, 1378–1388. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Martinez, L. Packmol: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W. (VMD)—(V)isual (M)olecular (D)ynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Zhou, G. A force field for molecular simulation of tetrabutylphosphonium amino acid ionic liquids. J. Phys. Chem. B 2007, 111, 7078–7084. [Google Scholar] [CrossRef] [PubMed]
- Sambasivarao, S. Development of OPLS-AA Force Field Parameters for 68 Unique Ionic Liquids. J. Chem. Theory Comput. 2009, 5, 1038–1050. [Google Scholar] [CrossRef]
- Våacha, R. Benchmarking Polarizable MD Simulation of Aqueous NaOH by Diffraction Measurements. J. Phys. Chem. A 2009, 113, 4022–4027. [Google Scholar] [CrossRef]
- Abascal, J.L. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Cornell, W.D. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef] [Green Version]
- Lorentz, H.A. Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase. Ann. D. Phys. 1881, 12, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Berthelot, D. Sur le mélange des gaz. C. R. Hebd. Acad. Sci. 1898, 126, 1703–1855. [Google Scholar]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Tuckerman, M. Reversible multiple time scale molecular dynamics. Am. Inst. Phys. 1992, 97, 1990–2001. [Google Scholar] [CrossRef] [Green Version]
- Hockney, R.W. Computer Simulation Using Particles; Hockney, R.W., Eastwood, J.W., Eds.; Taylor and Francis Group: New York, NY, USA, 1988; pp. 1–564. [Google Scholar]
- Isle-Holder, R.E. Reconsidering Dispersion Potentials: Reduced Cutoffs in Mesh-Based Ewald Solvers Can be Faster than Truncation. J. Comput. Chem. 2013, 9, 5412–5420. [Google Scholar]
- Ryckaert, J.P. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Flyvbjerg, H. Error estimates on averages of correlated data. J. Chem. Phys. 1989, 91, 461–466. [Google Scholar] [CrossRef]
- Jorgensen, W.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Price, D.J. A modified TIP3P water potential for simulation with Ewald summation. J. Chem. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef]
- Kirschner, K.N. GLYCAM06: A generalizable biomolecular force field. Carbohydrates. J. Comput. Chem. 2008, 29, 622–655. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q. Molecular Dynamics Simulation of Poly(ethylene terephthalate) Oligomers. J. Phys. Chem. B 2009, 114, 786–795. [Google Scholar] [CrossRef]
- Metzler, R. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [Green Version]
- Grebenkov, D.S. Time-averaged mean square displacement for switching diffusion. Phys. Rev. E 2019, 99, 032133. [Google Scholar] [CrossRef] [Green Version]
- Hanwell, M.D. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 1–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolfram Research, Inc. Mathematica Software; Software Version 12.0; Wolfram Research, Inc.: Champaign, IL, USA, 2019. [Google Scholar]
- Chempath, S. Density Functional Theory Study of Degradation of Tetraalkylammonium Hydroxides. J. Phys. Chem. C 2010, 114, 11977–11983. [Google Scholar] [CrossRef]
- Abe, H. Maintenance-Free Cellulose Solvents Based on Onium Hydroxides. ACS Sustain. Chem. Eng. 2015, 3, 1771–1776. [Google Scholar] [CrossRef]
- Tetrabutylphoshonium Hydroxide 40 wt% in H2O, Tetrabutylphoshonium Hydroxide (TBPH), CAS #14518-69-5; Sigma-Aldrich: St. Louis, MO, USA, 2017.
- Tetrabutylphoshonium Hydroxide 40 wt% in H2O, Tetrabutylphoshonium Hydroxide (TBPH), CAS #14518-69-5; Fisher Scientific: Fair Lawn, NJ, USA, 2017.
- Tetrabutylammonium Hydroxide (TBAH) 54–55% aq. solution extrapure AR, Tetrabutylammonium Hydroxide, CAS #2052-49-5; Sisco Research Laboratories Pvt. Ltd. (SRL): Maharashtra, India, 2017.
- Tetrabutylammonium Hydroxide 40 wt% in H2O, Tetrabutylammonium Hydroxide (TBAH), CAS #2052-49-5; Sigma-Aldrich: St. Louis, MO, USA, 2017.
- Tetrabutylammonium chloride 50 wt% in H2O, Tetrabutylammonium chloride (TBACl), CAS #1112-67-0; Fisher Scientific: Fair Lawn, NJ, USA, 2018.
- Haughney, M. Molecular-Dynamics Simulation of Liquid Methanol. J. Phys. Chem. 1987, 91, 4934–4940. [Google Scholar] [CrossRef]
- Hess, B. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Chowdhuri, S. Hydrogen Bonds in Aqueous Electrolyte Solutions: Statistics and Dynamics Based on Both Geometric and Energetic Criteria. Phys. Rev. E 2002, 66, 041203. [Google Scholar] [CrossRef]
- Chandra, A. Effects of Ion Atmosphere on Hydrogen-Bond Dynamics in Aqueous Electrolyte Solutions. Phys. Rev. Lett. 2000, 85, 768. [Google Scholar] [CrossRef]
- Luzar, A. Effect of Environment on Hydrogen Bond Dynamics in Liquid Water. Phys. Rev. Lett. 1996, 76, 928–931. [Google Scholar] [CrossRef]
- Luzar, A. Resolving the Hydrogen Bond Dynamics Conundrum. J. Chem. Phys. 2000, 113, 10663–10675. [Google Scholar] [CrossRef] [Green Version]
- Luzar, A. Structure and Hydrogen-Bond Dynamics of Water-Dimethyl Sulfoxide Mixtures by Computer-Simulations. J. Chem. Phys. 1993, 98, 8160–8173. [Google Scholar] [CrossRef] [Green Version]
- Luzar, A. Hydrogen-bond kinetics in liquid water. Nature 1996, 379, 55–57. [Google Scholar] [CrossRef]
- Ertl, P. JSME Molecule Editor. Available online: https://www.mn-am.com/online_demos/corina_demo_interactive (accessed on 1 June 2017).
- Sun, X. The reorientation mechanism of hydroxide ions in water: A molecular dynamics study. Chem. Phys. Lett. 2009, 481, 9–16. [Google Scholar] [CrossRef]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics; Smith, J.M., Van Ness, H.C., Abbott, M.M., Glandt, E.D., Klein, M.T., Edgar, T.F., Eds.; McGraw-Hill: Boston, MA, USA, 2005; pp. 1–817. [Google Scholar]
- Thompson, M.W. Scalable Screening of Soft Matter: A Case Study of Mixtures of Ionic Liquids and Organic Solvents. J. Phys. Chem. B 2019, 123, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, H. A jump motion of small molecules in glassy polymers: A molecular dynamics simulation. J. Chem. Phys. 1990, 93, 2062. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Diffusion of penetrants in amorphous polymers: A molecular dynamics study. J. Chem. Phys. 1991, 94, 3192–3199. [Google Scholar] [CrossRef]
- Zhang, W. Second-Generation ReaxFF Water Force Field: Improvements in the Description of Water Density and OH-Anion Diffusion. J. Phys. Chem. B 2017, 121, 6021–6032. [Google Scholar] [CrossRef]
- Mardoukhi, Y. Geometry controlled anomalous diffusion in random fractal geometries: Looking beyond the infinite cluster. Phys. Chem. Chem. Phys. 2015, 17, 30134–30147. [Google Scholar] [CrossRef] [Green Version]
- Menjoge, A. Influence of Water on Diffusion in Imidazolium-Based Ionic Liquids: A Pulsed Field Gradient NMR study. J. Phys. Chem. B. 2009, 113, 6353–6359. [Google Scholar] [CrossRef]
- Pace, S. Enrichment of microbial communities tolerant to the ionic liquids tetrabutylphosphonium chloride and tributylethylphosphonium diethylphosphate. Appl. Microbio. Biot. 2016, 100, 5639–5652. [Google Scholar] [CrossRef] [Green Version]
- Weiner, P.K. AMBER: Assisted model building with energy refinement. A general program for modeling molecules and their interactions. J. Comput. Chem. 1981, 2, 287–303. [Google Scholar] [CrossRef]
- Chempath, S. Mechanism of Tetraalkylammonium Headgroup Degradation in Alkaline Fuel Cell Membranes. J. Phys. Chem. C 2008, 112, 3179–3182. [Google Scholar] [CrossRef]
- Chowdhury, S. Reactivity of ionic liquids. Tetrahedron 2007, 63, 12363–12389. [Google Scholar] [CrossRef] [Green Version]
- Ye, Y. Relative Chemical Stability of Imidazolium-Based Alkaline Anion Exchange Polymerized Ionic Liquids. Macromolecules 2011, 44, 8494–8503. [Google Scholar] [CrossRef]
- Schröder, C. Comparing reduced partial charge models with polarizable simulations of ionic liquids. Phys. Chem. Chem. Phys. 2012, 14, 3089–3102. [Google Scholar] [CrossRef]



















| Mole% | Total | Total | Total | Total |
|---|---|---|---|---|
| Water | NIL | NH2O | Molecules | Atoms |
| 0.55 a | 180 | 1 | 181 | 9,903 |
| 5.26 | 180 | 10 | 190 | 9,930 |
| 10.0 | 180 | 20 | 200 | 9,960 |
| 20.0 | 180 | 45 | 225 | 10,035 |
| 30.0 | 180 | 77 | 257 | 10,131 |
| 40.0 | 180 | 120 | 300 | 10,260 |
| 50.0 | 170 | 170 | 340 | 9,860 |
| 60.0 | 165 | 248 | 413 | 9,819 |
| 70.0 | 160 | 374 | 534 | 9,922 |
| 80.0 | 150 | 600 | 750 | 10,050 |
| 85.0 | 140 | 794 | 934 | 10,082 |
| 90.0 | 120 | 1,080 | 1,200 | 9,840 |
| 92.5 b | 110 | 1,357 | 1,467 | 10,121 |
| 94.0 b | 100 | 1,567 | 1,667 | 10,201 |
| 95.0 | 90 | 1,710 | 1,800 | 10,080 |
| 99.0 | 30 | 2,970 | 3,000 | 10,560 |
| 99.97 a | 1 | 3,000 | 3,001 | 9,055 |
| TBPH–Water | |||
|---|---|---|---|
| Mole% | Mass Heat Capacity | Molar Heat Capacity | Thermal Expansivity |
| Water | cp, J g −1 K−1 | cp, J mol−1 K−1 | αp, 10−4 K−1 |
| 50.0 | 4.31 ± 0.17 | 634.7 ± 25.2 | 6.74 ± 0.39 |
| 60.0 | 4.33 ± 0.25 | 524.9 ± 29.8 | 6.57 ± 0.28 |
| 70.0 | 4.51 ± 0.21 | 430.7 ± 20.1 | 6.70 ± 0.26 |
| 80.0 | 4.72 ± 0.17 | 328.7 ± 12.2 | 7.33 ± 0.36 |
| 85.0 | 4.82 ± 0.16 | 273.7 ± 9.2 | 7.18 ± 0.21 |
| 90.0 | 4.89 ± 0.18 | 214.4 ± 8.1 | 7.65 ± 0.30 |
| 95.0 | 5.08 ± 0.16 | 157.3 ± 5.1 | 7.88 ± 0.23 |
| 99.0 | 5.10 ± 0.17 | 105.0 ± 3.4 | 4.93 ± 0.24 |
| 99.97 a | 4.95 ± 0.17 | 89.6 ± 3.0 | 3.07 ± 0.21 |
| 50.0 | 4.09 ± 0.21 | 639.9 ± 32.6 | 6.80 ± 0.22 |
| 60.0 | 4.08 ± 0.19 | 524.5 ± 24.5 | 7.30 ± 0.22 |
| 70.0 | 4.24 ± 0.19 | 428.2 ± 19.5 | 7.03 ± 0.22 |
| 80.0 | 4.46 ± 0.20 | 327.1 ± 14.5 | 7.38 ± 0.24 |
| 85.0 | 4.63 ± 0.21 | 275.7 ± 12.7 | 7.74 ± 0.36 |
| 90.0 | 4.75 ± 0.12 | 217.0 ± 5.6 | 7.50 ± 0.22 |
| 95.0 | 4.95 ± 0.20 | 157.7 ± 6.2 | 7.83 ± 0.28 |
| 99.0 | 5.06 ± 0.13 | 105.2 ± 2.7 | 4.77 ± 0.31 |
| 99.97 a | 4.96 ± 0.21 | 89.8 ± 3.8 | 3.03 ± 0.42 |
| Kα (10−6 cm2 s−1)/α (1/sα) | ||||||
|---|---|---|---|---|---|---|
| H2O | TBP+ | OH− | ||||
| Mole% | Kα | α | Kα | α | Kα | α |
| 50.0 | 0.423 | 0.329 | 0.179 | 0.375 | 0.434 | 0.331 |
| 60.0 | 0.496 | 0.304 | 0.151 | 0.320 | 0.440 | 0.289 |
| 70.0 | 1.01 | 0.315 | 0.203 | 0.360 | 0.657 | 0.249 |
| 80.0 | 1.82 | 0.536 | 0.297 | 0.496 | 0.786 | 0.390 |
| 85.0 | 2.80 | 0.749 | 0.455 | 0.693 | 1.03 | 0.588 |
| 90.0 | 7.17 | 0.917 | 1.01 | 0.872 | 2.16 | 0.855 |
| 92.5 | 12.2 | 0.954 | 1.62 | 0.894 | 3.65 | 0.937 |
| 94.0 | 17.2 | 0.977 | 2.34 | 0.935 | 5.97 | 0.934 |
| 95.0 | 22.1 | 0.975 | 2.93 | 0.932 | 8.22 | 0.949 |
| 99.0 | 87.3 | 1.00 | 14.7 | 0.978 | 43.5 | 0.969 |
| 99.97 a | 139 | 0.999 | – – | – – | – – | – – |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crawford, B.; Ismail, A.E. Thermodynamic and Transport Properties of Tetrabutylphosphonium Hydroxide and Tetrabutylphosphonium Chloride–Water Mixtures via Molecular Dynamics Simulation. Polymers 2020, 12, 249. https://doi.org/10.3390/polym12010249
Crawford B, Ismail AE. Thermodynamic and Transport Properties of Tetrabutylphosphonium Hydroxide and Tetrabutylphosphonium Chloride–Water Mixtures via Molecular Dynamics Simulation. Polymers. 2020; 12(1):249. https://doi.org/10.3390/polym12010249
Chicago/Turabian StyleCrawford, Brad, and Ahmed E. Ismail. 2020. "Thermodynamic and Transport Properties of Tetrabutylphosphonium Hydroxide and Tetrabutylphosphonium Chloride–Water Mixtures via Molecular Dynamics Simulation" Polymers 12, no. 1: 249. https://doi.org/10.3390/polym12010249
APA StyleCrawford, B., & Ismail, A. E. (2020). Thermodynamic and Transport Properties of Tetrabutylphosphonium Hydroxide and Tetrabutylphosphonium Chloride–Water Mixtures via Molecular Dynamics Simulation. Polymers, 12(1), 249. https://doi.org/10.3390/polym12010249