Study on the Pyrolysis Kinetics and Mechanisms of the Tread Compounds of Silica-Filled Discarded Car Tires
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.3. Pyrolysis Kinetics
2.3.1. Proposed Reaction Mechanism
2.3.2. Method for Solving Kinetic Parameters
2.3.3. Test method for kinetic parameters
3. Results and Analysis
3.1. Thermogravimetric Analysis
3.2. Kinetics Analysis
3.3. Reaction Mechanism Analysis
3.4. Model Reconstruction
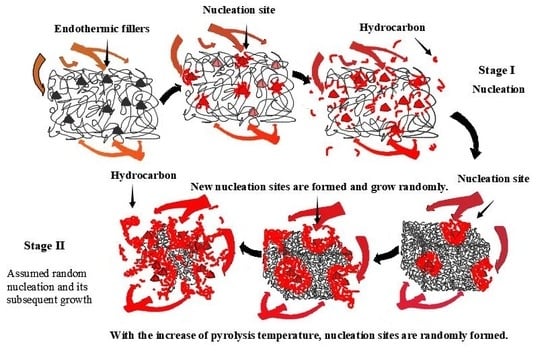
3.5. Reaction Principle Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- IRSG WWF. Available online: http://www.rubberstudy.com/news-article.aspx?id=5147&b=default.aspx (accessed on 3 March 2018).
- Oyedun, A.; Lam, K.-L.; Fittkau, M.; Hui, C.-W. Optimisation of particle size in waste tyre pyrolysis. Fuel 2012, 95, 417–424. [Google Scholar] [CrossRef]
- Salmasi, S.S.Z.; Abbas-Abadi, M.S.; Haghighi, M.N.; Abedini, H. The effect of different zeolite based catalysts on the pyrolysis of poly butadiene rubber. Fuel 2015, 160, 544–548. [Google Scholar] [CrossRef]
- Dębek, C.; Walendziewski, J. Hydrorefining of oil from pyrolysis of whole tyres for passenger cars and vans. Fuel 2015, 159, 659–665. [Google Scholar] [CrossRef]
- Chen, T.; Wu, J.; Zhang, Z.; Zhu, M.; Sun, L.; Wu, J.; Zhang, D. Key thermal events during pyrolysis and CO2-gasification of selected combustible solid wastes in a thermogravimetric analyser. Fuel 2014, 137, 77–84. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, C.; Chaos, M.; Chen, R.; Lu, S. Estimation of beech pyrolysis kinetic parameters by Shuffled Complex Evolution. Bioresour. Technol. 2016, 200, 658–665. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Xiao, H.-H.; He, J.-J.; Sun, Q.; Gong, L.; Sun, J.-H. Application of genetic algorithm to pyrolysis of typical polymers. Fuel Process. Technol. 2015, 138, 48–55. [Google Scholar] [CrossRef]
- Rehan, M.; Miandad, R.; Barakat, M.A.; Ismail, I.M.I.; Almeelbi, T.; Gardy, J.; Hassanpour, A.; Khan, M.Z.; Demirbas, A.; Nizami, A.S. Effect of zeolite catalysts on pyrolysis liquid oil. Int. Biodeterior. Biodegrad. 2017, 119, 162–175. [Google Scholar] [CrossRef]
- Guo, Q.; Yue, X.; Wang, M.; Liu, Y. Pyrolysis of scrap printed circuit board plastic particles in a fluidized bed. Powder Technol. 2010, 198, 422–428. [Google Scholar] [CrossRef]
- Ma, C.; Yan, Q.; Yu, J.; Chen, T.; Wang, D.; Liu, S.; Bikane, K.; Sun, L. The behavior of heteroatom compounds during the pyrolysis of waste computer casing plastic under various heating conditions. J. Clean. Prod. 2019, 219, 461–470. [Google Scholar] [CrossRef]
- Sogancioglu, M.; Yel, E.; Ahmetli, G. Pyrolysis of waste high density polyethylene (HDPE) and low density polyethylene (LDPE) plastics and production of epoxy composites with their pyrolysis chars. J. Clean. Prod. 2017, 165, 369–381. [Google Scholar] [CrossRef]
- Wu, M.; Zhao, M.; Chang, G.; Hu, X.; Guo, Q. A composite obtained from waste automotive plastics and sugarcane skin flour: Mechanical properties and thermo-chemical analysis. Powder Technol. 2019, 347, 27–34. [Google Scholar] [CrossRef]
- Jiang, T.; Liu, S.; AlMutawa, F.; Tanner, J.E.; Tan, G. Comprehensive reuse of pyrolysis chars from coals for fabrication of highly insulating building materials. J. Clean. Prod. 2019, 222, 424–435. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Omairey, E.; Cai, J.; Gu, F.; Bridgwater, A. V Intermediate pyrolysis of organic fraction of municipal solid waste and rheological study of the pyrolysis oil for potential use as bio-bitumen. J. Clean. Prod. 2018, 187, 390–399. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Yan, B.; Li, H.; Yu, S.; Liu, S.; Yu, H.; Ge, X. SO42−/ZrO2 as catalyst for upgrading of pyrolysis oil by esterification. Fuel 2018, 226, 190–194. [Google Scholar] [CrossRef]
- Cao, X.; Li, L.; Shitao, Y.; Liu, S.; Hailong, Y.; Qiong, W.; Ragauskas, A.J. Catalytic conversion of waste cooking oils for the production of liquid hydrocarbon biofuels using in-situ coating metal oxide on SBA-15 as heterogeneous catalyst. J. Anal. Appl. Pyrolysis 2019, 138, 137–144. [Google Scholar] [CrossRef]
- Qi, P.; Chang, G.; Wang, H.; Zhang, X.; Guo, Q. Production of aromatic hydrocarbons by catalytic co-pyrolysis of microalgae and polypropylene using HZSM-5. J. Anal. Appl. Pyrolysis 2018, 136, 178–185. [Google Scholar] [CrossRef]
- Chang, G.; Miao, P.; Wang, H.; Wang, L.; Hu, X.; Guo, Q. A synergistic effect during the co-pyrolysis of Nannochloropsis sp. and palm kernel shell for aromatic hydrocarbon production. Energy Convers. Manag. 2018, 173, 545–554. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, Z.; Cui, Z. Helical carbon nanofibers prepared by pyrolysis of acetylene with a catalyst derived from the decomposition of copper tartrate. Carbon N. Y. 2003, 41, 3072–3074. [Google Scholar] [CrossRef]
- Yu, L.; Sui, L.; Qin, Y.; Du, F.; Cui, Z. Catalytic synthesis of carbon nanofibers and nanotubes by the pyrolysis of acetylene with iron nanoparticles prepared using a hydrogen-arc plasma method. Mater. Lett. 2009, 63, 1677–1679. [Google Scholar] [CrossRef]
- Zhang, G.; He, Y.; Feng, Y.; Wang, H.; Zhang, T.; Xie, W.; Zhu, X. Enhancement in liberation of electrode materials derived from spent lithium-ion battery by pyrolysis. J. Clean. Prod. 2018, 199, 62–68. [Google Scholar] [CrossRef]
- Zhang, G.; He, Y.; Wang, H.; Feng, Y.; Xie, W.; Zhu, X. Application of mechanical crushing combined with pyrolysis-enhanced flotation technology to recover graphite and LiCoO2 from spent lithium-ion batteries. J. Clean. Prod. 2019, 231, 1418–1427. [Google Scholar] [CrossRef]
- Zhong, W.; Guo, Q.; Wang, X.; Zhang, L. Catalytic hydroprocessing of fast pyrolysis bio-oil from Chlorella. J. Fuel Chem. Technol. 2013, 41, 571–578. [Google Scholar] [CrossRef]
- Balasundram, V.; Ibrahim, N.; Kasmani, R.M.; Hamid, M.K.A.; Isha, R.; Hasbullah, H.; Ali, R.R. Thermogravimetric catalytic pyrolysis and kinetic studies of coconut copra and rice husk for possible maximum production of pyrolysis oil. J. Clean. Prod. 2017, 167, 218–228. [Google Scholar] [CrossRef]
- Han, D.; Yang, X.; Li, R.; Wu, Y. Environmental impact comparison of typical and resource-efficient biomass fast pyrolysis systems based on LCA and Aspen Plus simulation. J. Clean. Prod. 2019, 231, 254–267. [Google Scholar] [CrossRef]
- Duan, J.; Fang, L.; Gao, S.; Zhang, Z.; Wang, W. Numerical simulation and structural optimization of multi-compartment fluidized bed reactor for biomass fast pyrolysis. Chem. Eng. Process. 2019, 140, 114–126. [Google Scholar] [CrossRef]
- Li, Z.H.; Yuan, K.; Yu, Y.Z.; Liu, F.P.; Li, X.C. Study on Pyrolysis Methods and Equipment of the Waste Rubber. Advanced Mater. Res. 2014, 1052, 529–534. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Z.; Xu, D.; Guo, Q. Pyrolysis of waste plastic crusts of televisions. Environ. Technol. 2012, 33, 1987–1992. [Google Scholar] [CrossRef]
- Chang, G.; Miao, P.; Yan, X.; Wang, G.; Guo, Q. Phenol preparation from catalytic pyrolysis of palm kernel shell at low temperatures. Bioresour. Technol. 2018, 253, 214–219. [Google Scholar] [CrossRef]
- Koga, N.; Malek, J. Accommodation of the actual solid-state process in the kinetic model function. Part 2. Applicability of the empirical kinetic model function to diffusion-controlled reactions. Thermochim. Acta 1996, 282–283, 69–80. [Google Scholar] [CrossRef]
- Koga, N.; Tanaka, H. Accommodation of the actual solid-state process in the kinetic model function: I. Significance of the non-integral kinetic exponents. J. Therm. Anal. Calorim. 1994, 41, 455–469. [Google Scholar] [CrossRef]
- Murray, P.; White, J. Kinetics of the thermal dehydration of clays. Part IV. Interpretation of the differential thermal analysis of the clay minerals. Trans. Br. Ceram. Soc. 1955, 54, 204–238. [Google Scholar]
- Kissinger, H.E. Variation of peak temperature with heating rate in differential thermal analysis. J. Res. Natl. Bur. Stand. (1934) 1956, 57, 217–221. [Google Scholar] [CrossRef]
- Akahira, T. Trans. Joint convention of four electrical institutes. Res. Rep. Chiba Inst. Technol. 1971, 16, 22–31. [Google Scholar]
- Chen, R.; Li, Q.; Zhang, Y.; Xu, X.; Zhang, D. Pyrolysis kinetics and mechanism of typical industrial non-tyre rubber wastes by peak-differentiating analysis and multi kinetics methods. Fuel 2019, 235, 1224–1237. [Google Scholar] [CrossRef]
- Gonzalez, J.F.; Encinar, J.M.; Canito, J.L.; Rodriguez, J.J. Pyrolysis of automobile tires wastes. Influence of operating variable and kinetic study. Int. Symp. Anal. Appl. Pyrolysis 2001, 59, 667–683. [Google Scholar] [CrossRef]
- Mazloom, G.; Farhadi, F.; Khorasheh, F. Kinetic modeling of pyrolysis of scrap tires. J. Anal. Appl. Pyrolysis 2009, 84, 157–164. [Google Scholar] [CrossRef]
- Leung, D.Y.C.; Wang, C.L. Kinetic study of scrap tyre pyrolysis and combustion. J. Anal. Appl. Pyrolysis 1998, 45, 153–169. [Google Scholar] [CrossRef]
- Conesa, J.A.; Font, R.; Marcilla, A. Mass spectrometry validation of a kinetic model for the thermal decomposition of tyre wastes. J. Anal. Appl. Pyrolysis 1997, 43, 83–96. [Google Scholar] [CrossRef]
- Maciejewski, M. Computational aspects of kinetic analysis. Thermochim. Acta 2000, 355, 145–154. [Google Scholar] [CrossRef]
- Brown, M.E.; Maciejewski, M.; Vyazovkin, S.; Nomen, R.; Sempere, J.; Burnham, A.; Opfermann, J.; Strey, R.; Anderson, H.L.; Kemmler, A.; et al. Computational aspects of kinetic analysis Part A: The ICTAC Kinetics Project-data, methods and results. Thermochim. Acta 2000, 355, 125–143. [Google Scholar] [CrossRef]
- Kordoghli, S.; Khiari, B.; Paraschiv, M.; Zagrouba, F.; Tazerout, M. Production of hydrogen and hydrogen-rich syngas during thermal catalytic supported cracking of waste tyres in a bench-scale fixed bed reactor. Int. J. Hydrogen Energy 2019, 44, 11289–11302. [Google Scholar] [CrossRef]
- Kordoghli, S.; Paraschiv, M.; Kuncser, R.; Tazerout, M.; Zagrouba, F. Catalysts’ influence on thermochemical decomposition of waste tires. Environ. Prog. Sustain. Energy 2017, 36, 1560–1567. [Google Scholar] [CrossRef]
- Hilal DemirbaŞ, A. Yields and heating values of liquids and chars from spruce trunkbark pyrolysis. Energy Sources 2005, 27, 1367–1373. [Google Scholar] [CrossRef]
- Demirbas, A. Determination of calorific values of bio-chars and pyro-oils from pyrolysis of beech trunkbarks. J. Anal. Appl. Pyrolysis 2004, 72, 215–219. [Google Scholar] [CrossRef]
- Bridgwater, A. V Renewable fuels and chemicals by thermal processing of biomass. Chem. Eng. J. 2003, 91, 87–102. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. In Journal of Polymer Science Part C: Polymer Symposia; Wiley Online Library: New York, NY, USA, 1964; Volume 6, pp. 183–195. [Google Scholar]
- Starink, M.J. A new method for the derivation of activation energies from experiments performed at constant heating rate. Thermochim. Acta 1996, 288, 97–104. [Google Scholar] [CrossRef]
- Málek, J. The applicability of Johnson-Mehl-Avrami model in the thermal analysis of the crystallization kinetics of glasses. Thermochim. Acta 1995, 267, 61–73. [Google Scholar] [CrossRef]
- Šesták, J.; Málek, J. Diagnostic limits of phenomenological models of heterogeneous reactions and thermal analysis kinetics. Solid State Ionics 1993, 63, 245–254. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, J.; Wu, S.; Wang, B.; Wang, Z. Pyrolysis kinetics of phenol–formaldehyde resin by non-isothermal thermogravimetry. Carbon N. Y. 2010, 48, 352–358. [Google Scholar] [CrossRef]
- Vlaev, L.; Nedelchev, N.; Gyurova, K.; Zagorcheva, M. A comparative study of non-isothermal kinetics of decomposition of calcium oxalate monohydrate. J. Anal. Appl. Pyrolysis 2008, 81, 253–262. [Google Scholar] [CrossRef]
- Liqing, L.; Donghua, C. Application of iso-temperature method of multiple rate to kinetic analysis. J. Therm. Anal. Calorim. 2004, 78, 283–293. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, D.; Li, M.; He, J.-J.; Gao, Z.-H.; Zhou, Y.; Sun, J.-H. Pyrolytic behavior of waste extruded polystyrene and rigid polyurethane by multi kinetics methods and Py-GC/MS. Fuel 2018, 222, 11–20. [Google Scholar] [CrossRef]
- Ding, Y.; Ezekoye, O.A.; Zhang, J.; Wang, C.; Lu, S. The effect of chemical reaction kinetic parameters on the bench-scale pyrolysis of lignocellulosic biomass. Fuel 2018, 232, 147–153. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, D.; Gu, J.; Bao, B.; Zhang, Q. Determination of pyrolysis characteristics and kinetics of palm kernel shell using TGA–FTIR and model-free integral methods. Energy Convers. Manag. 2015, 89, 251–259. [Google Scholar] [CrossRef]
- Lopez, G.; Aguado, R.; Olazar, M.; Arabiourrutia, M.; Bilbao, J. Kinetics of scrap tyre pyrolysis under vacuum conditions. Waste Manag. 2009, 29, 2649–2655. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Park, J.K.; Chun, H.D. Pyrolysis kinetics of scrap tire rubbers. I: Using DTG and TGA. J. Environ. Eng. (USA) 1995, 121, 507–514. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Cherbański, R.; Wróblewski, K.; Molga, E. Pyrolysis of waste tyres–The effect of reaction kinetics on the results of thermogravimetric analysis. Chem. Process Eng. 2017, 38, 363–377. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-state kinetic models: Basics and mathematical fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef]
- Senneca, O.; Salatino, P.; Chirone, R. A fast heating-rate thermogravimetric study of the pyrolysis of scrap tyres. Fuel 1999, 78, 1575–1581. [Google Scholar] [CrossRef]
- Encinar, J.M.; González, J.F.; González, J. Fixed-bed pyrolysis of Cynara cardunculus L. Product yields and compositions. Fuel Process. Technol. 2000, 68, 209–222. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, Y.; Meng, D.; Jiao, T.; Qin, X.; Bai, G.; Liang, P. Effect of ash and dolomite on the migration of sulfur from coal pyrolysis volatiles. J. Anal. Appl. Pyrolysis 2019, 140, 349–354. [Google Scholar] [CrossRef]










| Tread rubber | Mixed ingredients (PHR) | ||||||
| SBR | NR | TSR20 | Silica | V700 | N234 | Antilux | |
| 15 | 105 | 20 | 70 | 13 | 18 | 3 | |
| Si69 | SAD | DPG | ZnO | S | CZ | 4040 | |
| 13 | 3 | 1 | 2 | 1.15 | 2 | 2 | |
| Inner liner | Mixed ingredients (PHR) | ||||||
| BR9000 | SBR | TSR20 | N234 | TDAE | RD | ||
| 15 | 15 | 70 | 45 | 3 | 1.5 | ||
| SAD | ZnO | Antilux | 6PPD | CBS | S | ||
| 3 | 3.5 | 1.5 | 2 | 1.5 | 1.8 | ||
| No. | Rate-Determining Mechanism | ||
|---|---|---|---|
| 1. Chemical process or mechanism non-invoking equations | |||
| 1 | Chemical reaction | ||
| 2 | Chemical reaction | ||
| 3 | Chemical reaction | ||
| 4 | Chemical reaction | ||
| 5 | Chemical reaction | ||
| 6 | Chemical reaction | ||
| 7 | Chemical reaction | ||
| 8 | Chemical reaction | ||
| 9 | Chemical reaction | ||
| 2. Acceleratory rate equations | |||
| 10 | Nucleation | ||
| 11 | Nucleation | ||
| 12 | Nucleation | ||
| 13 | Nucleation | ||
| 14 | Nucleation | ||
| 3. Sigmoidal rate equations or random nucleation and subsequent growth | |||
| 15 | Assumed random nucleation and its subsequent growth | ||
| 16 | Assumed random nucleation and its subsequent growth | ||
| 17 | Assumed random nucleation and its subsequent growth | ||
| 18 | Assumed random nucleation and its subsequent growth | ||
| 19 | Assumed random nucleation and its subsequent growth | ||
| 20 | Assumed random nucleation and its subsequent growth | ||
| 21 | Assumed random nucleation and its subsequent growth | ||
| 22 | Assumed random nucleation and its subsequent growth | ||
| 23 | Branching nuclei | ||
| 4. Deceleratory rate equations | |||
| 4.1. Phase boundary reaction | |||
| 24 | Contracting disk | ||
| 25 | Contracting cylinder (cylindrical symmetry) | ||
| 26 | Contracting sphere (spherical symmetry) | ||
| 4.2. Based on the diffusion mechanism | |||
| 27 | One-dimensional diffusion | ||
| 28 | Two-dimensional diffusion | ||
| 29 | Two-dimensional diffusion | ||
| 30 | Three-dimensional diffusion, spherical symmetry | ||
| 31 | Three-dimensional diffusion, cylindrical symmetry | ||
| 32 | Three-dimensional diffusion | ||
| 33 | Three-dimensional diffusion | ||
| 34 | Three-dimensional diffusion | ||
| 35 | Three-dimensional diffusion | ||
| 36 | Three-dimensional diffusion | ||
| Reaction I | No. of equation | 10 | 11 | 12 | 13 | 27 | ||||
| Test results | Slope | −0.36 | −0.12 | −0.08 | −0.06 | −0.48 | ||||
| R2 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | |||||
| Reaction II | No. of equation | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | |
| Test results | Slope | −0.45 | −0.30 | −0.22 | −0.14 | −0.11 | −0.90 | −1.34 | −1.79 | |
| R2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | ||
| Reaction A | No. of equation | 35 | ||||||||
| Test results | Slope | −1.07 | ||||||||
| R2 | 0.99 | |||||||||
| Reaction B | No. of equation | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | |
| Test results | Slope | −0.64 | −0.43 | −0.32 | −0.21 | −0.16 | −1.28 | −1.92 | −2.56 | |
| R2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | ||
| Function Name | Mechanism | ||
|---|---|---|---|
| Power law model | Acceleration curve, Nucleation | ||
| J-A-M equation | Assumed random nucleation and its subsequent growth |
| Reaction | Model | n | R2 | Result Test | |||
|---|---|---|---|---|---|---|---|
| Slope | R2 | ||||||
| I | Power-law model | 0.2473 | 0.99 | −0.98 | 0.98 | ||
| II | J-A-M equation | 0.4142 | 0.99 | −1.08 | 0.99 | ||
| B | J-A-M equation | 0.5405 | 0.99 | −1.00 | 0.99 | ||
| Research Object | Degradation Temperature Range (K) | Activation Energy (kJ/mol) | Pre-Exponential Factor (1/min) | Source |
|---|---|---|---|---|
| Reaction I | 500–645 | 155.26 | 1.29 × 1012 | This study |
| Reaction II | 645–750 | 315.40 | 2.92 × 1022 | |
| Tread rubber | 500–750 | 237.05 | 2.92 × 1022 | |
| Reaction A | 515–650 | 219.89 | 3.94 × 1019 | |
| Reaction B | 650–720 | 300.58 | 1.35 × 1021 | |
| Inner liner | 515–720 | 280.72 | 1.35 × 1021 | |
| Tread rubber of unknown tire | 300–773 | 33–283 | 7.56 × 102–1.39 × 1019 | [2,60] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhao, B.; Tian, X.; Wang, K.; Tian, Z.; Han, W.; Bian, H. Study on the Pyrolysis Kinetics and Mechanisms of the Tread Compounds of Silica-Filled Discarded Car Tires. Polymers 2020, 12, 810. https://doi.org/10.3390/polym12040810
Wang C, Zhao B, Tian X, Wang K, Tian Z, Han W, Bian H. Study on the Pyrolysis Kinetics and Mechanisms of the Tread Compounds of Silica-Filled Discarded Car Tires. Polymers. 2020; 12(4):810. https://doi.org/10.3390/polym12040810
Chicago/Turabian StyleWang, Chuansheng, Baishun Zhao, Xiaolong Tian, Kongshuo Wang, Zhongke Tian, Wenwen Han, and Huiguang Bian. 2020. "Study on the Pyrolysis Kinetics and Mechanisms of the Tread Compounds of Silica-Filled Discarded Car Tires" Polymers 12, no. 4: 810. https://doi.org/10.3390/polym12040810
APA StyleWang, C., Zhao, B., Tian, X., Wang, K., Tian, Z., Han, W., & Bian, H. (2020). Study on the Pyrolysis Kinetics and Mechanisms of the Tread Compounds of Silica-Filled Discarded Car Tires. Polymers, 12(4), 810. https://doi.org/10.3390/polym12040810