Deformation Properties of Concentrated Metal-in-Polymer Suspensions under Superimposed Compression and Shear
Abstract
:1. Introduction
2. Materials and Methods
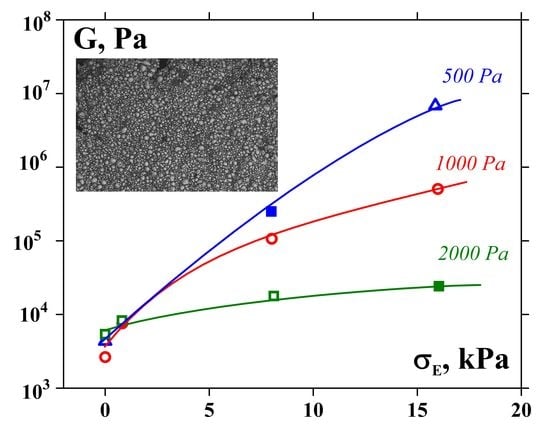
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guazzelli, É.; Pouliquen, O. Rheology of dense granular suspensions. J. Fluid. Mech. 2018, 852. [Google Scholar] [CrossRef] [Green Version]
- Tanner, R.I. Review: Rheology of noncolloidal suspensions with non-Newtonian matrices. J. Rheol. 2019, 63, 705–717. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Mityukov, A.V.; Kotomin, S.V.; Shabeko, A.A.; Kulichikhin, V.G. Elasticity and plasticity of highly concentrated noncolloidal suspensions under shear. J. Rheol. 2020, 64, 469–479. [Google Scholar] [CrossRef]
- Malkin, A.; Kulichikhin, V.; Ilyin, S. A modern look on yield stress fluids. Rheol. Acta 2017, 56, 177–188. [Google Scholar] [CrossRef]
- Sherwood, J.D.; Durban, D. Squeeze flow of a power-law viscoplastic solid. J. Non Newton. Fluid Mech. 1996, 62, 35–54. [Google Scholar] [CrossRef]
- Adams, M.J.; Aydin, İ.; Briscoe, B.J.; Sinha, S.K. A finite element analysis of the squeeze flow of an elasto-viscoplastic paste material. J. Non Newton. Fluid Mech. 1997, 71, 41–57. [Google Scholar] [CrossRef]
- Roussel, N.; Lanos, C. Plastic Fluid Flow Parameters Identification Using a Simple Squeezing Test. Appl. Rheol. 2003, 13, 132–141. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Patlazhan, S.A. Wall slip for complex liquids—Phenomenon and its causes. Adv. Colloid Interf. Sci. 2018, 257, 42–57. [Google Scholar] [CrossRef]
- Cloitre, M.; Bonnecaze, R.T. A review on wall slip in high solid dispersions. Rheol. Acta 2017, 56, 283–305. [Google Scholar] [CrossRef]
- He, J.; Lee, S.S.; Kalyon, D.M. Shear viscosity and wall slip behavior of dense suspensions of polydisperse particles. J. Rheol. 2018, 63, 19–32. [Google Scholar] [CrossRef]
- Wagner, N.J.; Brady, J.F. Shear thickening in colloidal dispersions. Phys. Today 2009, 62, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Cwalina, C.D.; Wagner, N.J. Material properties of the shear-thickened state in concentrated near hard-sphere colloidal dispersions. J. Rheol. 2014, 58, 949–967. [Google Scholar] [CrossRef]
- Seto, R.; Mari, R.; Morris, J.F.; Denn, M.M. Discontinuous Shear Thickening of Frictional Hard-Sphere Suspensions. Phys. Rev. Lett. 2013, 111, 218301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mutch, K.J.; Laurati, M.; Amann, C.P.; Fuchs, M.; Egelhaaf, S.U. Time-dependent flow in arrested states—Transient behaviour. Eur. Phys. J. Spec. Top. 2013, 222, 2803–2817. [Google Scholar] [CrossRef] [Green Version]
- Brown, E.; Jaeger, H.M. Dynamic Jamming Point for Shear Thickening Suspensions. Phys. Rev. Lett. 2009, 103, 086001. [Google Scholar] [CrossRef] [Green Version]
- Denn, M.M.; Morris, J.F. Rheology of Non-Brownian Suspensions. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 203–228. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Kulichikhin, V.G. Shear thickening and dynamic glass transition of concentrated suspensions. State of the problem. Colloid J. 2016, 78, 1–8. [Google Scholar] [CrossRef]
- Hsiao, L.C.; Jamali, S.; Glynos, E.; Green, P.F.; Larson, R.G.; Solomon, M.J. Rheological State Diagrams for Rough Colloids in Shear Flow. Phys. Rev. Lett. 2017, 119, 158001. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Mari, R.; Denn, M.M.; Morris, J.F. A constitutive model for simple shear of dense frictional suspensions. J. Rheol. 2018, 62, 457–468. [Google Scholar] [CrossRef]
- Zmievski, V.; Grmela, M.; Bousmina, M.; Dagréou, S. Nonlinear microstructure and rheology of semidilute colloidal suspensions of structureless particles. Phys. Rev. E 2005, 71, 051503. [Google Scholar] [CrossRef]
- Boromand, A.; Jamali, S.; Grove, B.; Maia, J.M. A generalized frictional and hydrodynamic model of the dynamics and structure of dense colloidal suspensions. J. Rheol. 2018, 62, 905–918. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.-Q. Strain localization during squeeze of an entangled polymer melt under constant force. J. Rheol. 2018, 62, 491–499. [Google Scholar] [CrossRef]
- Varga, Z.; Swan, J.W. Large scale anisotropies in sheared colloidal gels. J. Rheol. 2018, 62, 405–418. [Google Scholar] [CrossRef]
- Alonso-Marroquín, F.; Luding, S.; Herrmann, H.J.; Vardoulakis, I. Role of anisotropy in the elastoplastic response of a polygonal packing. Phys. Rev. E 2005, 71, 051304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kawabata, H.; Nishiura, D.; Sakaguchi, H.; Tatsumi, Y. Self-organized domain microstructures in a plate-like particle suspension subjected to rapid simple shear. Rheol. Acta 2013, 52, 1–21. [Google Scholar] [CrossRef]
- Montesi, A.; Peña, A.A.; Pasquali, M. Vorticity Alignment and Negative Normal Stresses in Sheared Attractive Emulsions. Phys. Rev. Lett. 2004, 92, 058303. [Google Scholar] [CrossRef] [Green Version]
- Sommer, D.E.; Favaloro, A.J.; Pipes, R.B. Coupling anisotropic viscosity and fiber orientation in applications to squeeze flow. J. Rheol. 2018, 62, 669–679. [Google Scholar] [CrossRef]
- De Cagny, H.; Fall, A.; Denn, M.M.; Bonn, D. Local rheology of suspensions and dry granular materials. J. Rheol. 2015, 59, 957–969. [Google Scholar] [CrossRef] [Green Version]
- Fall, A.; Ovarlez, G.; Hautemayou, D.; Mézière, C.; Roux, J.-N.; Chevoir, F. Dry granular flows: Rheological measurements of the μ(I)-rheology. J. Rheol. 2015, 59, 1065–1080. [Google Scholar] [CrossRef] [Green Version]
- Møller, P.C.F.; Rodts, S.; Michels, M.A.J.; Bonn, D. Shear banding and yield stress in soft glassy materials. Phys. Rev. E 2008, 77, 041507. [Google Scholar] [CrossRef] [Green Version]
- Miller, J. A complex fluid exhibits unexpected heterogeneous flow. Phys. Today 2010, 63, 18. [Google Scholar] [CrossRef]
- Laun, H.M.; Münstedt, H. Elongational behaviour of a low density polyethylene melt. Rheol. Acta 1978, 17, 415–425. [Google Scholar] [CrossRef]
- Laun, H.M. Prediction of Elastic Strains of Polymer Melts in Shear and Elongation. J. Rheol. 1986, 30, 459–501. [Google Scholar] [CrossRef]
- Khan, S.A.; Prud’homme, R.K.; Larson, R.G. Comparison of the rheology of polymer melts in shear, and biaxial and uniaxial extensions. Rheol. Acta 1987, 26, 144–151. [Google Scholar] [CrossRef]
- Gabriel, C.; Münstedt, H. Creep recovery behavior of metallocene linear low-density polyethylenes. Rheol. Acta 1999, 38, 393–403. [Google Scholar] [CrossRef]
- Wolff, F.; Resch, J.A.; Kaschta, J.; Münstedt, H. Comparison of viscous and elastic properties of polyolefin melts in shear and elongation. Rheol. Acta 2009, 49, 95. [Google Scholar] [CrossRef]
- Patham, B.; Jayaraman, K. Creep recovery of random ethylene-octene copolymer melts with varying comonomer content. J. Rheol. 2005, 49, 989–999. [Google Scholar] [CrossRef]
- Resch, J.A.; Stadler, F.J.; Kaschta, J.; Münstedt, H. Temperature Dependence of the Linear Steady-State Shear Compliance of Linear and Long-Chain Branched Polyethylenes. Macromolecules 2009, 42, 5676–5683. [Google Scholar] [CrossRef]
- Rolón-Garrido, V.H.; Resch, J.A.; Wolff, F.; Kaschta, J.; Münstedt, H.; Wagner, M.H. Prediction of steady-state viscous and elastic properties of polyolefin melts in shear and elongation. Rheol. Acta 2011, 50, 645–653. [Google Scholar] [CrossRef]
- Lodge, A.S. Elastic Liquids; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Malkin, A.Y.; Isayev, A. Rheology: Conceptions, Methods, and Applications; ChemTec Publishing: Toronto, ON, Canada, 2017. [Google Scholar]
- O’Brien, C.J.; Foiles, S.M. Exploration of the mechanisms of temperature-dependent grain boundary mobility: Search for the common origin of ultrafast grain boundary motion. J. Mater. Sci. 2016, 51, 6607–6623. [Google Scholar] [CrossRef]
- Fall, A.; Bertrand, F.; Hautemayou, D.; Mezière, C.; Moucheront, P.; Lemaître, A.; Ovarlez, G. Macroscopic Discontinuous Shear Thickening versus Local Shear Jamming in Cornstarch. Phys. Rev. Lett. 2015, 114, 098301. [Google Scholar] [CrossRef] [PubMed]
- Saw, S.; Grob, M.; Zippelius, A.; Heussinger, C. Unsteady flow, clusters, and bands in a model shear-thickening fluid. Phys. Rev. E 2020, 101, 012602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rathee, V.; Blair, D.L.; Urbach, J.S. Localized transient jamming in discontinuous shear thickening. J. Rheol. 2020, 64, 299–308. [Google Scholar] [CrossRef] [Green Version]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malkin, A.Y.; Kulichikhin, V.G.; Mityukov, A.V.; Kotomin, S.V. Deformation Properties of Concentrated Metal-in-Polymer Suspensions under Superimposed Compression and Shear. Polymers 2020, 12, 1038. https://doi.org/10.3390/polym12051038
Malkin AY, Kulichikhin VG, Mityukov AV, Kotomin SV. Deformation Properties of Concentrated Metal-in-Polymer Suspensions under Superimposed Compression and Shear. Polymers. 2020; 12(5):1038. https://doi.org/10.3390/polym12051038
Chicago/Turabian StyleMalkin, Alexander Ya., Valery G. Kulichikhin, Anton V. Mityukov, and Sergey V. Kotomin. 2020. "Deformation Properties of Concentrated Metal-in-Polymer Suspensions under Superimposed Compression and Shear" Polymers 12, no. 5: 1038. https://doi.org/10.3390/polym12051038
APA StyleMalkin, A. Y., Kulichikhin, V. G., Mityukov, A. V., & Kotomin, S. V. (2020). Deformation Properties of Concentrated Metal-in-Polymer Suspensions under Superimposed Compression and Shear. Polymers, 12(5), 1038. https://doi.org/10.3390/polym12051038