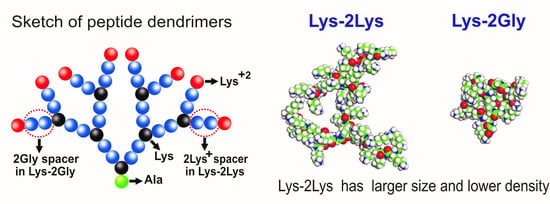
Comparison of Structure and Local Dynamics of Two Peptide Dendrimers with the Same Backbone but with Different Side Groups in Their Spacers
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. The Global Characteristics
3.2. The Local Structure
3.3. Orientational Mobility and NMR Relaxation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buhleier, E.; Wehner, E.; Vogtle, F. “Cascade” and “nonskid-chain-like” syntheses of molecular cavity topologies. Synthesis 1978, 78, 155–158. [Google Scholar] [CrossRef]
- Frechet, M.J.; Tomalia, D.A. (Eds.) Dendrimers and Other Dendritic Polymer, 1st ed.; Wiley: London, UK, 2001. [Google Scholar] [CrossRef]
- Bourne, N.; Stanberry, L.R.; Kern, E.R.; Holan, G.; Matthews, B.; Bernstein, D.I. Dendrimers, a new class of candidate topical microbicides with activity against herpes simplex virus infection. Antimicrob. Agents Chemother. 2000, 44, 2471–2474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sherje, A.P.; Jadhav, M.; Dravyakar, B.R.; Kadam, D. Dendrimers: A versatile nanocarrier for drug delivery and targeting. Int. J. Pharm. 2018, 548, 707–720. [Google Scholar] [CrossRef] [PubMed]
- Madaan, K.; Kumar, S.; Poonia, N.; Lather, V.; Pandita, D. Dendrimers in drug delivery and targeting: Drug-dendrimer interactions and toxicity issues. J. Pharm. Bioallied Sci. 2014, 6, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Bielinska, A.; Kukowska-Latallo, J.F.; Johnson, J.; Tomalia, D.A.; Baker, J.R., Jr. Regulation of in vitro gene expression using antisense oligonucleotides or antisense expression plasmids transfected using starburst PAMAM dendrimers. Nucleic Acids Res. 1996, 24, 2176–2182. [Google Scholar] [CrossRef] [Green Version]
- Dutta, T.; Jain, N.K.; McMillan, N.A.; Parekh, H.S. Dendrimer nanocarriers as versatile vectors in gene delivery. Nanomedicine 2010, 6, 25–34. [Google Scholar] [CrossRef]
- Ionov, M.; Lazniewska, J.; Dzmitruk, V.; Halets, I.; Loznikova, S.; Novopashina, D.; Apartsin, E.; Krasheninina, O.; Venyaminova, A.; Milowska, K.; et al. Anticancer siRNA cocktails as a novel tool to treat cancer cells. Part (A). Mechanisms of interaction. Int. J. Pharm. 2015, 485, 261–269. [Google Scholar] [CrossRef]
- Dzmitruk, V.; Szulc, A.; Shcharbin, D.; Janaszewska, A.; Shcharbina, N.; Lazniewska, J.; Novopashina, D.; Buyanova, M.; Ionov, M.; Klajnert-Maculewicz, B.; et al. Anticancer siRNA cocktails as a novel tool to treat cancer cells. Part (B). Efficiency of pharmacological action. Int. J. Pharm. 2015, 485. [Google Scholar] [CrossRef]
- Yamamoto, K.; Imaoka, T.; Tanabe, M.; Kambe, T. New Horizon of Nanoparticle and Cluster Catalysis with Dendrimers. Chem. Rev. 2020, 120, 1397–1437. [Google Scholar] [CrossRef]
- Denkewalter, R.G.; Kolc, J.; Lukasavage, W.J. Preparation of Lysine Based Macromolecular Highly Branched Compound. U.S. Patent No. 4 (360), 646, 6 April 1979. [Google Scholar]
- Denkewalter, R.G.; Kolc, J.; Lukasavage, W.J. Macromolecular Highly Branched Homogeneous Compound Based on Lysine Units. U.S. Patent No. 4 (289), 872, 15 September 1981. [Google Scholar]
- Vlasov, G.P.; Korol’kov, V.I.; Pankova, G.A.; Tarasenko, I.I.; Baranov, A.N.; Glazkov, P.B.; Kiselev, A.V.; Ostapenko, O.V.; Lesina, E.A.; Baranov, V.S. Lysine Dendrimers and Their Starburst Polymer Derivatives: Possible Application for DNA Compaction and in vitro Delivery of Genetic Constructs. Russ. J. Bioorg. Chem. 2004, 30, 12. [Google Scholar] [CrossRef]
- McCarthy, T.D.; Karellas, P.; Henderson, S.A.; Giannis, M.; O’Keefe, D.F.; Heery, G.; Paull, J.; Matthews, B.R.; Holan, G. Dendrimers as drugs: Discovery and preclinical and clinical development of dendrimer-based microbicides for HIV and STI prevention. Mol. Pharm. 2005, 2, 312–318. [Google Scholar] [CrossRef] [PubMed]
- Patri, A.K.; Majoros, I.J.; Baker, J.R. Dendritic polymer macromolecular carriers for drug delivery. Curr. Opin. Chem. Biol. 2002, 6, 466–471. [Google Scholar] [CrossRef]
- Fox, M.E.; Guillaudeu, S.; Frechet, J.M.; Jerger, K.; Macaraeg, N.; Szoka, F.C. Synthesis and in vivo antitumor efficacy of PEGylated poly (l-lysine) dendrimer-camptothecin conjugates. Mol. Pharm. 2009, 6, 1562–1572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaminskas, L.M.; Kelly, B.D.; McLeod, V.M.; Sberna, G.; Owen, D.J.; Boyd, B.J.; Porter, C.J. Characterisation and tumour targeting of PEGylated polylysine dendrimers bearing doxorubicin via a pH labile linker. J. Control. Release 2011, 152, 241–248. [Google Scholar] [CrossRef]
- Al-Jamal, K.; Al-Jamal, W.; Wang, J.; Rubio, N.; Buddle, J.; Gathercole, D.; Zloh, M.; Kestrels, K. Cationic poly-L-lysine dendrimer complexes doxorubicin and delays tumor growth in vitro and in vivo. ACS Nano 2013, 7, 1905–1917. [Google Scholar] [CrossRef]
- Ohsaki, M.; Okuda, T.; Wada, A.; Hirayama, T.; Niidome, T.; Aoyagi, H. In vitro gene transfection using dendritic poly (L-lysine). Bioconjug. Chem. 2002, 13, 510–517. [Google Scholar] [CrossRef]
- Okuda, T.; Kidoaki, S.; Ohsaki, M.; Koyama, Y.; Yoshikawa, K.; Niidome, T.; Aoyagi, H. Time-dependent complex formation of dendritic poly (L-lysine) with plasmid DNA and correlation with in vitro transfection efficiencies. Org. Biomol. Chem. 2003, 1, 1270–1273. [Google Scholar] [CrossRef]
- Cong, H.; Wang, K.; Zhou, Z.; Yang, J.; Piao, Y.; Yu, B.; Shen, Y.; Zhou, Z. Tuning the Brightness and Photostability of Organic Dots for Multivalent Targeted Cancer Imaging and Surgery. ACS Nano 2020, 14, 5887–5900. [Google Scholar] [CrossRef]
- Al-Jamal, K.T.; Akerman, S.; Podesta, J.E.; Yilmazer, A.; Turton, J.A.; Bianco, A.; Vargesson, N.; Kanthou, C.; Florence, A.T.; Tozer, G.M.; et al. Systemic antiangiogenic activity of cationic poly-l-lysine dendrimer delays tumor growth. Proc. Natl. Acad. Sci. USA 2010, 107, 3966–3971. [Google Scholar] [CrossRef] [Green Version]
- Boyd, B.J.; Kaminskas, L.M.; Karellas, P.; Krippner, G.; Lessene, R.; Porter, C.J. Cationic poly-l-lysine dendrimers: Pharmacokinetics, biodistribution, and evidence for metabolism and bioresorption after intravenous administration to rats. Mol. Pharm. 2006, 3, 614–627. [Google Scholar] [CrossRef]
- Isaksson, K.; Akerberg, D.; Posaric-Bauden, M.; Andersson, R.; Tingstedt, B. In vivo toxicity and biodistribution of intraperitoneal and intravenous poly-l-lysine and poly-l-lysine/poly-l-glutamate in rats. J. Mater. Sci. Mater. Med. 2014, 25, 1293–1299. [Google Scholar] [CrossRef]
- Aharoni, S.M.; Crosby, C.R., III; Walsh, E.K. Size and solution properties of globular tert-butyloxycarbonyl-poly(α,ϵ-l-lysine). Macromolecules 1982, 15, 1093–1098. [Google Scholar] [CrossRef]
- Aharoni, S.; Murthy, M. Spherical non-draining BOC-poly-(α,ϵ-l-lysine) macromolecules SAX and viscous study. Polym. Commun. 1983, 24, 132. [Google Scholar]
- Neelov, I.; Falkovich, S.; Markelov, D.; Paci, E.; Darinskii, A.; Tenhu, H. Molecular Dynamics of Lysine Dendrimers. Computer Simulation and NMR. In Dendrimers in Biomedical Applications; Royal Society of Chemistry: London, UK, 2013; pp. 99–114. [Google Scholar] [CrossRef]
- Neelov, I.; Markelov, D.; Falkovich, S.; Ilyash, M.; Okrugin, B.; Darinskii, A. Mathematical simulation of lysine dendrimers. Temperature dependencies. Polym. Sci. Ser. C 2013, 55, 154–161. [Google Scholar] [CrossRef]
- Markelov, D.A.; Falkovich, S.G.; Neelov, I.M.; Ilyash, M.Y.; Matveev, V.V.; Lahderanta, E.; Ingman, P.; Darinskii, A.A. Molecular dynamics simulation of spin–lattice NMR relaxation in poly-l-lysine dendrimers: Manifestation of the semiflexibility effect. Phys. Chem. Chem. Phys. 2015, 17, 3214–3226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roberts, B.P.; Scanlon, M.J.; Krippner, G.Y.; Chalmers, D.K. Molecular Dynamics of Poly(l-lysine) Dendrimers with Naphthalene Disulfonate Caps. Macromolecules 2009, 42, 2775–2783. [Google Scholar] [CrossRef]
- Falkovich, S.; Markelov, D.; Neelov, I.; Darinskii, A. Are structural properties of dendrimers sensitive to the symmetry of branching? Computer simulation of lysine dendrimers. J. Chem. Phys. 2013, 139, 064903. [Google Scholar] [CrossRef]
- Shavykin, O.; Mikhailov, I.; Darinskii, A.; Neelov, I.; Leermakers, F. Effect of an asymmetry of branching on structural characteristics of dendrimers revealed by Brownian dynamics simulations. Polymer 2018, 146, 256–266. [Google Scholar] [CrossRef]
- Shavykin, O.; Neelov, I.; Darinskii, A. Is the Manifestation of the Local Dynamics in the Spin-Lattice NMR Relaxation in Dendrimers Sensitive to Excluded Volume Interactions. Phys. Chem. Chem. Phys. 2016, 18, 24307–24317. [Google Scholar] [CrossRef] [Green Version]
- Dalakoglou, G.; Karatasos, K.; Lyulin, S.; Larin, S.; Darinskii, A.; Lyulin, A. Conformational Effects in Non-Stoichiometric Complexes of Two Hyperbranched Molecules with a Linear Polyelectrolyte. Polymers 2002, 4, 240–255. [Google Scholar] [CrossRef] [Green Version]
- Shavykin, O.V.; Leermakers, F.A.; Neelov, I.M.; Darinskii, A.A. Self-Assembly of Lysine-Based Dendritic Surfactants Modeled by the Self-Consistent Field Approach. Langmuir 2018, 34, 1613–1626. [Google Scholar] [CrossRef]
- Rao, C.; Tam, J.P. Synthesis of peptide dendrimer. J. Am. Chem. Soc. 1994, 116, 6975–6976. [Google Scholar] [CrossRef]
- Tam, J.P. Synthetic peptide vaccine design: Synthesis and properties of a high-density multiple antigenic peptide system. Proc. Natl. Acad. Sci. USA 1988, 85, 5409–5413. [Google Scholar] [CrossRef] [Green Version]
- Vlasov, G.; Tarasenko, I.; Valueva, S.; Kipper, A.; Tarabukina, E.; Filippov, A.; Avdeeva, E.; Vorob’ev, V.I. Hyperbranched Poly(l-lysine) Containing Additional Amino Acids or Their Oligomers Between Branching Points: Synthesis and Structure. Polym. Sci. Ser. A 2005, 47, 422–429. [Google Scholar] [CrossRef]
- Crespo, L.; Sanclimens, G.; Pons, M.; Giralt, E.; Royo, M.; Albericio, F. Peptide and amide bond-containing dendrimers. Chem. Rev. 2005, 105, 1663–1682. [Google Scholar] [CrossRef]
- Choi, J.S.; Nam, K.; Park, J.y.; Kim, J.B.; Lee, J.K.; Park, J.S. Enhanced Transfection Efficiency of PAMAM Dendrimer by Surface Modification with l-Arginine. J. Control. Release 2004, 99, 445–456. [Google Scholar] [CrossRef]
- Aldawsari, H.; Raj, B.S.; Edrada-Ebel, R.; Blatchford, D.R.; Tate, R.J.; Tetley, L.; Dufès, C. Enhanced gene expression in tumors after intravenous administration of arginine-, lysine- and leucine-bearing polyethylenimine polyplex. Nanomed. Nanotechnol. Biol. Med. 2011, 7, 615–623. [Google Scholar] [CrossRef]
- Delort, E.; Darbre, T.; Reymond, J.L. A strong positive dendritic effect in a peptide dendrimer-catalyzed ester hydrolysis reaction. J. Am. Chem. Soc. 2004, 126, 15642–15643. [Google Scholar] [CrossRef]
- Darbre, T.; Reymond, J.L. Peptide dendrimers as artificial enzymes, receptors, and drug-delivery agents. Acc. Chem. Res. 2006, 39, 925–934. [Google Scholar] [CrossRef]
- Javor, S.; Delort, E.; Darbre, T.; Reymond, J.L. A peptide dendrimer enzyme model with a single catalytic site at the core. J. Am. Chem. Soc. 2007, 129, 13238–13246. [Google Scholar] [CrossRef]
- Polcyn, P.; Zielinska, P.; Zimnicka, M.; Troc, A.; Kalicki, P.; Solecka, J.; Laskowska, A.; Urbanczyk-Lipkowska, Z. Novel antimicrobial peptide dendrimers with amphiphilic surface and their interactions with phospholipids—Insights from mass spectrometry. Molecules 2013, 18, 7120–7144. [Google Scholar] [CrossRef] [Green Version]
- Pires, J.; Siriwardena, T.; Stach, M.; Tinguely, R.; Kasraian, S.; Luzzaro, F.; Leib, S.; Darbre, T.; Reymond, J.L.; Endimiani, A. In Vitro Activity of the Novel Antimicrobial Peptide Dendrimer G3KL against Multidrug-Resistant Acinetobacter baumannii and Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 2015, 59, 7915–7918. [Google Scholar] [CrossRef] [Green Version]
- Klajnert, B.; Janiszewska, J.; Urbanczyk-Lipkowska, Z.; Bryszewska, M.; Shcharbin, D.; Labieniec, M. Biological properties of low molecular mass peptide dendrimers. Int. J. Pharm. 2006, 309, 208–217. [Google Scholar] [CrossRef]
- Manikkath, J.; Hegde, A.R.; Kalthur, G.; Parekh, H.S.; Mutalik, S. Influence of peptide dendrimers and sonophoresis on the transdermal delivery of ketoprofen. Int. J. Pharm. 2017, 521, 110–119. [Google Scholar] [CrossRef] [Green Version]
- Santos, S.; Gonzaga, R.; Silva, J.; Savino, D.; Prieto, D.; Shikay, J.; Silva, R.; Paulo, L.; Ferreira, E.; Giarolla, J. Peptide dendrimers: Drug/gene delivery and other approaches. Can. J. Chem. 2017, 95, 907–916. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhang, Q.; Chang, H.; Cheng, Y. Surface-engineered dendrimers in gene delivery. Chem. Rev. 2015, 115, 5274–5300. [Google Scholar] [CrossRef]
- Kwok, A.; Eggimann, G.; Reymond, J.; Darbre, T.; Hollfelder, F. Peptide dendrimer/lipid hybrid systems are efficient DNA transfection reagents: Structure-activity relationships highlight the role of charge distribution across dendrimer generations. ACS Nano 2013, 7, 4668–4682. [Google Scholar] [CrossRef]
- Kwok, A.; Eggimann, G.; Heitz, M.; Reymond, J.L.; Hollfelder, F.; Darbre, T.; Darbre, T. Efficient Transfection of siRNA by Peptide Dendrimer–Lipid Conjugates. Chem. Biol. Chem. 2016, 17, 2223–2229. [Google Scholar] [CrossRef] [Green Version]
- Mannisto, M.; Vanderkerken, S.; Toncheva, V.; Elomaa, M.; Ruponen, M.; Schacht, E.; Urtti, A. Structure–activity relationships of poly (l-lysines): Effects of pegylation and molecular shape on physicochemical and biological properties in gene delivery. J. Control. Release 2002, 83, 169–182. [Google Scholar] [CrossRef]
- Luo, K.; Li, C.; Wang, G.; Nie, Y.; He, B.; Wu, Y.; Gu, Z. Peptide dendrimers as efficient and biocompatible gene delivery vectors: Synthesis and in vitro characterization. J. Control. Release 2011, 155, 77–87. [Google Scholar] [CrossRef]
- Luo, K.; Li, C.; Li, L.; She, W.; Wang, G.; Gu, Z. Arginine functionalized peptide dendrimers as potential gene delivery vehicles. Biomaterials 2012, 33, 4917–4927. [Google Scholar] [CrossRef]
- Rewatkar, P.V.; Parekh, H.S.; Parat, M.O. Molecular determinants of the cellular entry of asymmetric peptide dendrimers and role of caveolae. PLoS ONE 2016, 11, e0147491. [Google Scholar] [CrossRef] [PubMed]
- Gorzkiewicz, M.; Konopka, M.; Janaszewska, A.; Tarasenko, I.I.; Sheveleva, N.N.; Gajek, A.; Neelov, I.M.; Klajnert-Maculewicz, B. Application of new lysine-based peptide dendrimers D3K2 and D3G2 for gene delivery: Specific cytotoxicity to cancer cells and transfection in vitro. Bioorg. Chem. 2020, 95, 103504. [Google Scholar] [CrossRef] [PubMed]
- Gorzkiewicz, M.; Kopec, O.; Janaszewska, A.; Konopka, M.; Pedziwiatr-Werbicka, E.; Tarasenko, I.I.; Bezrodnyi, V.V.; Neelov, I.M.; Klajnert-Maculewicz, B. Poly(lysine) Dendrimers Form Complexes with siRNA and Provide Its Efficient Uptake by Myeloid Cells: Model Studies for Therapeutic Nucleic Acid Delivery. Int. J. Mol. Sci. 2020, 21, 3138. [Google Scholar] [CrossRef]
- Mikhailov, I.; Darinskii, A. Does symmetry of branching affect the properties of dendrimers? Polym. Sci. Ser. A 2014, 56, 534–544. [Google Scholar] [CrossRef]
- Filipe, L.C.S.; Machuqueiro, M.; Darbre, T.; Baptista, A.M. Exploring the Structural Properties of Positively Charged Peptide Dendrimers. J. Phys. Chem. B 2016, 120, 11323–11330. [Google Scholar] [CrossRef] [Green Version]
- Filipe, L.C.S.; Campos, S.R.R.; Machuqueiro, M.; Darbre, T.; Baptista, A.M. Structuring peptide dendrimers through pH modulation and substrate binding. J. Phys. Chem. B 2016, 120, 10138–10152. [Google Scholar] [CrossRef]
- Okrugin, B.; Neelov, I.; Leermakers, F.M.; Borisov, O. Structure of asymmetrical peptide dendrimers: Insights given by self-consistent field theory. Polymer 2017, 125, 292–302. [Google Scholar] [CrossRef]
- Sheveleva, N.N.; Markelov, D.A.; Vovk, M.A.; Mikhailova, M.E.; Tarasenko, I.I.; Neelov, I.M.; Lahderanta, E. NMR studies of excluded volume interactions in peptide dendrimers. Sci. Rep. 2018, 8, 8916. [Google Scholar] [CrossRef] [Green Version]
- Sheveleva, N.N.; Markelov, D.A.; Vovk, M.A.; Mikhailova, M.E.; Tarasenko, I.I.; Tolstoy, P.M.; Neelov, I.M.; Lähderanta, E. Lysine-based dendrimer with double arginine residues. RSC Adv. 2019, 9, 18018–18026. [Google Scholar] [CrossRef] [Green Version]
- Sheveleva, N.N.; Markelov, D.A.; Vovk, M.A.; Tarasenko, I.I.; Mikhailova, M.E.; Ilyash, M.Y.; Neelov, I.M.; Lahderanta, E. Stable Deuterium Labeling of Histidine-Rich Lysine-Based Dendrimers. Molecules 2019, 24, 2481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yevlampieva, N.; Dobrodumov, A.; Nazarova, O.; Okatova, O.; Cottet, H. Hydrodynamic Behavior of Dendrigraft Polylysines in Water and Dimethylformamide. Polymers 2012, 4, 20–31. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Pall, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. Software X 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [Green Version]
- Mazo, M.A.; Shamaev, M.Y.; Balabaev, N.K.; Darinskii, A.A.; Neelov, I.M. Conformational mobility of carbosilane dendrimer: Molecular dynamics simulation. Phys. Chem. Chem. Phys. 2004, 6, 1285–1289. [Google Scholar] [CrossRef]
- Kurbatov, A.O.; Balabaev, N.K.; Kramarenko, E.Y. A Comparative Study of Intramolecular Mobility of Single Siloxane and Carbosilane Dendrimers via Molecular Dynamics Simulations. Polymers 2018, 10, 838. [Google Scholar] [CrossRef] [Green Version]
- Okrugin, B.; Ilyash, M.; Markelov, D.; Neelov, I. Lysine dendrigraft nanocontainers. Influence of topology on their size and internal structure. Pharmaceutics 2018, 10, 129. [Google Scholar] [CrossRef] [Green Version]
- Neelov, I.; Adolf, D. Brownian dynamics simulations of dendrimers under elongational flow: Bead-rod model with hydrodynamic interactions. Macromolecules 2003, 36, 6914–6924. [Google Scholar] [CrossRef]
- Neelov, I.; Adolf, D. Brownian dynamics simulation of hyperbranched polymers under elongational flow. Phys. Chem. B 2004, 108, 7627–7636. [Google Scholar] [CrossRef]
- Darinsky, A.; Lyulin, A.; Neelov, I. Computer simulations of molecular motion in liquid crystals by the method of Brownian dynamics. Macromol. Theory Simul. 1993, 2, 523–530. [Google Scholar] [CrossRef]
- Darinskii, A.; Gotlib, Y.; Lyulin, A.; Neyelov, L. Computer simulation of local dynamics of a polymer chain in the orienting field of the LC type. Vysokomol. Soedin. Ser. A 1991, 33, 1211–1220. [Google Scholar] [CrossRef]
- Darinskii, A.; Gotlib, Y.; Lukyanov, M.; Lyulin, A.; Neelov, I. Computer simulation of the molecular motion in LC and oriented polymers. In Application of Scattering Methods to the Dynamics of Polymer Systems; Ewen, B., Fischer, E., Fytas, G., Eds.; Progress in Colloid & Polymer Science; Springer: Berlin, Germany, 1993; Volume 91, pp. 13–15. [Google Scholar] [CrossRef]
- Neelov, I.M.; Binder, K. Brownian dynamics of grafted polymer chains: Time-dependent properties. Macromol. Theory Simul. 1995, 4, 1063–1084. [Google Scholar] [CrossRef]
- Neelov, I.; Adolf, D.; McLeish, T.; Paci, E. Molecular dynamics simulation of dextran extension by constant force in single molecule AFM. Biophys. J. 2006, 91, 3579–3588. [Google Scholar] [CrossRef] [Green Version]
- Gowdy, J.; Batchelor, M.; Neelov, I.; Paci, E. Nonexponential kinetics of loop formation in proteins and peptides: A signature of rugged free energy landscapes? J. Phys. Chem. B 2017, 121, 9518–9525. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ennari, J.; Elomaa, M.; Neelov, I.; Sundholm, F. Modeling of water-free and water containing solid polyelectrolytes. Polymer 2000, 41, 985–990. [Google Scholar] [CrossRef]
- Ennari, J.; Neelov, I.; Sundholm, F. Molecular dynamics simulation of the PEO sulfonic acid anion in water. Comput. Theor. Polym. Sci. 2000, 10, 403–410. [Google Scholar] [CrossRef]
- Ennari, J.; Neelov, I.; Sundholm, F. Simulation of a PEO based solid polyelectrolyte, comparison of the CMM and the Ewald summation method. Polymer 2000, 41, 2149–2155. [Google Scholar] [CrossRef]
- Ennari, J.; Neelov, I.; Sundholm, F. Molecular dynamics simulation of the structure of PEO based solid polymer electrolytes. Polymer 2000, 41, 4057–4063. [Google Scholar] [CrossRef]
- Ennari, J.; Neelov, I.; Sundholm, F. Estimation of the ion conductivity of a PEO-based polyelectrolyte system by molecular modeling. Polymer 2001, 42, 8043–8050. [Google Scholar] [CrossRef]
- Ennari, J.; Neelov, I.; Sunholm, F. Modelling of gas transport properties of polymer electrolytes containing various amounts of water. Polymer 2004, 45, 4171–4179. [Google Scholar] [CrossRef]
- Neelov, I.; Adolf, D.; Lyulin, A.; Davies, G. Brownian dynamics simulation of linear polymers under elongational flow: Bead–rod model with hydrodynamic interactions. J. Chem. Phys. 2002, 117, 4030–4041. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.; Postma, J.; DiNola, A.; Haak, J. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Evans, D.; Holian, B.L. The Nose–Hoover thermostat. J. Chem. Phys. 1985, 83, 4069. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1982, 52, 7182. [Google Scholar] [CrossRef]
- Kell, G.S. Isothermal Compressibility of liquid Water at 1 Atm. J. Chem. Eng. Data 1970, 15, 119–122. [Google Scholar] [CrossRef]
- Rosmalen, M.; Krom, M.; Merkx, M. Tuning the Flexibility of Glycine-Serine Linkers To Allow Rational Design of Multidomain Proteins. Biochemistry 2017, 56, 6565–6574. [Google Scholar] [CrossRef]
- Shaitan, K.; Mikhailyuk, M.; Leont’ev, K.; Saraikin, S.; Belyakov, A.A. Molecular dynamics of bending fluctuations of the elements of protein secondary structure. Biophysics 2002, 47, 411–419. [Google Scholar]
- Klein, J.; Jiang, S.; Galimidi, R.; Keeffe, J.R.; Bjorkman, P. Design and characterization of structured protein linkers with differing flexibilities. Protein Eng. Des. Sel. 2014, 27, 325–330. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. The Course of Theoretical Physics. Mechanics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1976; Volume 1, p. 224. [Google Scholar] [CrossRef]
- Klos, J.; Sommer, J. Properties of Dendrimers with Flexible Spacer-Chains: A Monte Carlo Study. Macromolecules 2009, 42, 4878–4886. [Google Scholar] [CrossRef]
- Theodorou, D.N.; Suter, U.W. Shape of unperturbed linear polymers: Polypropylene. Macromolecules 1985, 18, 1206–1214. [Google Scholar] [CrossRef]
- Rudnick, G.; Gaspari, G. The aspherity of random walks. J. Phys. A 1986, 4, L191. [Google Scholar] [CrossRef]
- Maiti, P.; Cagin, T.; Wang, G.; Goddard, W. Structure of PAMAM Dendrimers: Generations 1 through 11. Macromolecules 2004, 37, 6236–6254. [Google Scholar] [CrossRef]
- Zacharopoulos, N.; Economou, I. Morphology and Organization of Poly(propylene imine) Dendrimers in the Melt from Molecular Dynamics Simulation. Macromolecules 2002, 35, 1814–1821. [Google Scholar] [CrossRef]
- Burchard, W. Solution Properties of Branched Macromolecules. In Advances in Polymer Science; Springer: Berlin, Germany, 1999; Volume 143, pp. 113–194. [Google Scholar] [CrossRef]
- Nygaard, M.; Kragelund, B.B.; Papaleo, E.; Lindorff-Larsen, K. An Efficient Method for Estimating the Hydrodynamic Radius of Disordered Protein Conformations. Biophys. J. 2017, 113, 550–557. [Google Scholar] [CrossRef] [Green Version]
- Kirkwood, J.G. The general theory of irreversible processes in solutions of macromolecules. J. Polym. Sci. Polym. Phys. Ed. 1954, 12, 1–14. [Google Scholar] [CrossRef]
- Kollman, P.A.; Allen, L.C. Theory of the hydrogen bond. Chem. Rev. 1972, 72, 283–303. [Google Scholar] [CrossRef]
- Jeffrey, G.A.; Saenger, W. (Eds.) Hydrogen Bonding in Biological Structures, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1991; p. 569. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83. [Google Scholar] [CrossRef]
- Martinho, N.; Silva, L.; Florindo, H.; Brocchini, S.; Zloh, M.; Barata, T. Rational design of novel, fluorescent, tagged glutamic acid dendrimers with different terminal groups and in silico analysis of their properties. Int. J. Nanomed. 2017, 112, 7053–7073. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Ran, Q.; Haag, R.; Ballauff, M.; Dzubiella, J. Charged Dendrimers Revisited: Effective Charge and Surface Potential of Dendritic Polyglycerol Sulfate. Macromolecules 2017, 50, 4759–4769. [Google Scholar] [CrossRef] [Green Version]
- Klos, J.S. The Poisson-Boltzmann-Flory Approach to Charged Dendrimers: Effect of Generation and Spacer Length. Macromolecules 2019, 52, 3625–3635. [Google Scholar] [CrossRef]
- Delgado, A.V.; Gonzalez-Caballero, F.; Hunter, R.J.; Koopal, L.K.; Lyklema, J. Measurement and interpretation of electrokinetic phenomena. Pure Appl. Chem. 2005, 77, 1753–1805. [Google Scholar] [CrossRef] [Green Version]
- Ohshima, H. Theory of Colloid and Interfacial Electric Phenomena. Interface Science and Technology; Academic Press: Cambridge, MA, USA, 2006; Volume 12, p. 473. [Google Scholar] [CrossRef]
- Wolterink, J.K.; Leermakers, F.A.; Fleer, G.J.; Koopal, L.K.; Zhulina, E.B.; Borisov, O.V. Screening in Solutions of Star-Branched Polyelectrolytes. Macromolecules 1999, 32, 2365. [Google Scholar] [CrossRef]
- Gotlib, Y.Y.; Balabaev, N.K.; Darinskii, A.A.; Neelov, I.M. Investigation of Local Motions in Polymers by the Method of Molecular Dynamics. Macromolecules 1980, 13, 602–608. [Google Scholar] [CrossRef]
- Markelov, D.; Dolgushev, M.; Lahderanta, E. NMR Relaxation in Dendrimers. Annu. Rep. NMR Spectrosc. 2017, 91, 1–66. [Google Scholar] [CrossRef]
- Kimmich, R. (Ed.) NMR—Tomography, Diffusometry, Relaxometry; Springer: Germany, Berlin, 1997. [Google Scholar] [CrossRef]
- Kruk, D.; Herrmann, A.; Rossler, E.A. Field-Cycling NMR Relaxometry of Viscous Liquids and Polymers. Prog. Nucl. Magn. Reson. Spectrosc. 2012, 63, 33–64. [Google Scholar] [CrossRef]
- Gupta, S.; Biswas, P. Orientational Relaxation of Poly(propylene imine) Dendrimers at Different pH. J. Phys. Chem. 2020. [Google Scholar] [CrossRef]
- Gotlib, Y.; Markelov, D. Permittivity of a dendrimer containing polar groups. Polym. Sci. Ser. A 2004, 46, 815–832. [Google Scholar] [CrossRef]
- Gotlib, Y.Y.; Markelov, D.A. Theory of Orientational Relaxation of Individual Specified Units in a Dendrimer. Polym. Sci. Ser. A 2007, 49, 1137–1154. [Google Scholar] [CrossRef]
- Markelov, D.A.; Dolgushev, M.; Gotlib, Y.Y.; Blumen, A. NMR relaxation of the orientation of single segments in semiflexible dendrimers. J. Chem. Phys. 2014, 140, 244904. [Google Scholar] [CrossRef] [Green Version]
- Grimm, J.; Dolgushev, M. Dynamics of internally functionalized dendrimers. Phys. Chem. Chem. Phys. 2016, 18, 19050–19061. [Google Scholar] [CrossRef] [Green Version]
- Sheveleva, N.N.; Dolgushev, M.; Lähderanta, E.; Markelov, D.A. NMR Relaxation of Functionalized Dendrimers. Macromolecules 2019, 52, 9766–9772. [Google Scholar] [CrossRef]
- Markelov, D.A.; Lyulin, S.V.; Gotlib, Y.Y.; Lyulin, A.V.; Matveev, V.V.; Lahderanta, E.; Darinskii, A.A. Orientational mobility and relaxation spectra of dendrimers: Theory and computer simulation. J. Chem. Phys. 2009, 130, 044907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Markelov, D.A.; Gotlib, Y.Y.; Darinskii, A.A.; Lyulin, A.V.; Lyulin, S.V. Local Orientational Mobility in Dendrimers. Theory and Computer-Aided Simulation. Polym. Sci. Ser. A 2009, 51, 331–339. [Google Scholar] [CrossRef]
- Karatasos, K.; Adolf, D.; Davies, G. Statics and dynamics of model dendrimers as studied by molecular dynamics simulations. J. Chem. Phys. 2001, 115, 5310–5318. [Google Scholar] [CrossRef] [Green Version]
- Karatasos, K.; Lyulin, A. Local polymer dynamics under strong connectivity constraints: The dendrimer case. J. Chem. Phys. 2006, 15, 184907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sadovnichy, V.; Tikhonravov, A.; Voevodin, V.; Opanasenko, V. “Lomonosov”: Supercomputing at Moscow State University. In Contemporary High Performance Computing: From Petascale toward Exascale; Chapman and Hall/CRC: London, UK, 2013; pp. 283–307. [Google Scholar] [CrossRef]

















| Dendrimer | M (g/mol) | (e) | (e) | (e) | (nm) | |||
|---|---|---|---|---|---|---|---|---|
| Lys-2Lys | 5695.08 | +44 | 16 | +16 | 28 | +28 | 13,228 | 7.5 |
| Lys-2Gly | 3675.44 | +16 | 16 | +16 | 28 | 0 | 13,396 | 7.5 |
| Temperature | Lys-2Lys | Lys-2Gly |
|---|---|---|
| 280 K | 13.7 | 3.6 |
| 290 K | 10.5 | 3.2 |
| 300 K | 9.0 | 2.8 |
| 310 K | 7.0 | 2.1 |
| 320 K | 5.5 | 2.0 |
| 340 K | 5.1 | 1.3 |
| Dendrimer | [nm] | [nm] | [nm] | [nm] | [nm] | ||
|---|---|---|---|---|---|---|---|
| Lys-2Lys | 2.04 | 1.68 | 0.83 | 2.63 | 2.71 | 3.14 | 0.02 |
| Lys-2Gly | 1.27 | 1.12 | 0.89 | 1.64 | 1.93 | 2.43 | 0.01 |
| Dendrimer | (e) | (e/nm) | (mV) | ||||
|---|---|---|---|---|---|---|---|
| Lys-2Lys | 1.52 | 179.17 | 5.69 | 13.18 | 0.30 | 0.11 | 17.27 |
| Lys-2Gly | 7.68 | 100.68 | 0.67 | 9.39 | 0.59 | 0.13 | 20.03 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikhtaniuk, S.E.; Bezrodnyi, V.V.; Shavykin, O.V.; Neelov, I.M.; Sheveleva, N.N.; Penkova, A.V.; Markelov, D.A. Comparison of Structure and Local Dynamics of Two Peptide Dendrimers with the Same Backbone but with Different Side Groups in Their Spacers. Polymers 2020, 12, 1657. https://doi.org/10.3390/polym12081657
Mikhtaniuk SE, Bezrodnyi VV, Shavykin OV, Neelov IM, Sheveleva NN, Penkova AV, Markelov DA. Comparison of Structure and Local Dynamics of Two Peptide Dendrimers with the Same Backbone but with Different Side Groups in Their Spacers. Polymers. 2020; 12(8):1657. https://doi.org/10.3390/polym12081657
Chicago/Turabian StyleMikhtaniuk, Sofia E., Valeriy V. Bezrodnyi, Oleg V. Shavykin, Igor M. Neelov, Nadezhda N. Sheveleva, Anastasia V. Penkova, and Denis A. Markelov. 2020. "Comparison of Structure and Local Dynamics of Two Peptide Dendrimers with the Same Backbone but with Different Side Groups in Their Spacers" Polymers 12, no. 8: 1657. https://doi.org/10.3390/polym12081657
APA StyleMikhtaniuk, S. E., Bezrodnyi, V. V., Shavykin, O. V., Neelov, I. M., Sheveleva, N. N., Penkova, A. V., & Markelov, D. A. (2020). Comparison of Structure and Local Dynamics of Two Peptide Dendrimers with the Same Backbone but with Different Side Groups in Their Spacers. Polymers, 12(8), 1657. https://doi.org/10.3390/polym12081657