AC Electrokinetics of Salt-Free Multilayered Polymer-Grafted Particles
Abstract
:1. Introduction
2. Model
- The equilibrium electric field on the surface must satisfy the Gauss law:
- Impermeability to ions:
- Stagnancy of the liquid:
- Discontinuity of the normal component of the displacement vector ( is the relative permittivity of the particle). Using Equations (4) and (10), and the continuity of the potential,
- Continuity of the potential and of the normal displacement vector:
- Continuity of the normal and tangential components of the fluid velocity:
- Continuity of the vorticity and the pressure ( is the density of the solution):
- Continuity of ionic concentrations and velocities:
- Electroneutrality of the cell for the equilibrium:
- The macroscopic quantities are the result of averages of local quantities in the cell volume [42]:
3. Materials and Methods
3.1. Materials
3.2. Methods
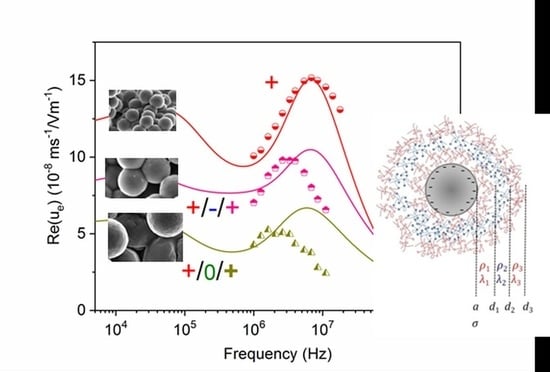
4. Results and Discussion
4.1. Model Predictions
4.2. Particle Characterization
4.3. Dynamic Mobility and Permittivity of the Suspensions. Predictions and Experiments
5. Limitations and Future Scope of the Model
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stark, W.J.; Stoessel, P.R.; Wohlleben, W.; Hafner, A. Industrial applications of nanoparticles. Chem. Soc. Rev. 2015, 44, 5793–5805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kestell, A.E.; DeLorey, G.T. Nanoparticles: Properties, Classification, Characterization; Nova Science Publishers: Hauppauge, NY, USA, 2009. [Google Scholar]
- Delgado, A.V.; López-Viota, J.; Ramos-Tejada, M.M.; Arias, J.L. Particle geometry, charge, and wettability: The fate of nanoparticle-based drug vehicles. In Colloid and Interface Science in Pharmaceutical Research and Development; Oshima, H., Ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Petros, R.A.; DeSimone, J.M. Strategies in the design of nanoparticles for therapeutic applications. Nat. Rev. Drug Discov. 2010, 9, 615–627. [Google Scholar] [CrossRef] [PubMed]
- Hume, D.A. The mononuclear phagocyte system. Curr. Opin. Immunol. 2006, 18, 49–53. [Google Scholar] [CrossRef]
- Howard, M.D.; Jay, M.; Dziublal, T.D.; Lu, X. PEGylation of nanocarrier drug delivery systems: State of the art. J. Biomed. Nanotechnol. 2008, 4, 133–148. [Google Scholar] [CrossRef]
- Deng, J.; He, J.; Zheng, J.-S.; Terakawa, S.; Huang, H.; Fang, L.-C.; Li, Y.; Cheng, P.; Jiang, L.-L. Preparation and Application of Amino- and Dextran-Modified Superparamagnetic Iron Oxide Nanoparticles. Part. Sci. Technol. 2013, 31, 241–247. [Google Scholar] [CrossRef]
- Gulbake, A.; Jain, S.K. Chitosan: A potential polymer for colon-specific drug delivery system. Expert Opin. Drug Deliv. 2012, 9, 713–729. [Google Scholar] [CrossRef]
- Dobrovolskaia, M.A.; Aggarwal, P.; Hall, J.B.; McNeil, S.E. Preclinical studies to understand nanoparticle interaction with the immune system and its potential effects on nanoparticle biodistribution. Mol. Pharm. 2008, 5, 487–495. [Google Scholar] [CrossRef] [Green Version]
- Canton, I.; Battaglia, G. Endocytosis at the nanoscale. Chem. Soc. Rev. 2012, 41, 2718–2739. [Google Scholar] [CrossRef]
- Pietronave, S.; Iafisco, M.; Locarno, D.; Rimondini, L.; Prat, M. Functionalized nanomaterials for diagnosis and therapy of cancer. J. Appl. Biomater. Biomech. 2009, 7, 77–89. [Google Scholar]
- Allen, T.M. Ligand-targeted therapeutics in anticancer therapy. Nat. Rev. Cancer 2002, 2, 750–763. [Google Scholar] [CrossRef]
- Del Mar Ramos-Tejada, M.; Viota, J.L.; Rudzka, K.; Delgado, A.V. Preparation of multi-functionalized Fe3O4/Au nanoparticles for medical purposes. Colloids Surf. B Biointerfaces 2015, 128, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merlin, J.; Duval, J.F.L. Electrodynamics of soft multilayered particles dispersions: Dielectric permittivity and dynamic mobility. Phys. Chem. Chem. Phys. 2014, 16, 15173–15188. [Google Scholar] [CrossRef] [PubMed]
- Duval, J.F.L.; Werner, C.; Zimmermann, R. Electrokinetics of soft polymeric interphases with layered distribution of anionic and cationic charges. Curr. Opin. Colloid Interface Sci. 2016, 24, 1–12. [Google Scholar] [CrossRef]
- Ohshima, H. Theory of electrostatics and electrokinetics of soft particles. Sci. Technol. Adv. Mater. 2009, 10. [Google Scholar] [CrossRef] [PubMed]
- Decher, G.; Hong, J.D.; Schmitt, J. Buildup of ultrathin multilayer films by a self-assembly process. 3. consecutively alternating adsorption of anionic and cationic polyelectrolytes on charged surfaces. Thin Solid Films 1992, 210, 831–835. [Google Scholar] [CrossRef]
- Decher, G. Fuzzy nanoassemblies: Toward layered polymeric multicomposites. Science 1997, 277, 1232–1237. [Google Scholar] [CrossRef]
- Oosawa, F. Thermodynamic properties of rodlike polyelectrolyte solutions in presence of salts. J. Polym. Sci. A 1963, 1, 1501–1508. [Google Scholar] [CrossRef]
- Medebach, M.; Palberg, T. Phenomenology of colloidal crystal electrophoresis. J. Chem. Phys. 2003, 119, 3360–3370. [Google Scholar] [CrossRef]
- Wette, P.; Schope, H.J.; Palberg, T. Experimental determination of effective charges in aqueous suspensions of colloidal spheres. Colloids Surf. A Physicochem. Eng. Asp. 2003, 222, 311–321. [Google Scholar] [CrossRef]
- Medebach, M.; Palberg, T. Electrophoretic mobility of electrostatically interacting colloidal spheres. J. Phys. Condens. Matter 2004, 16, 5653–5658. [Google Scholar] [CrossRef]
- Palberg, T.; Medebach, M.; Garbow, N.; Evers, M.; Fontecha, A.B.; Reiber, H.; Bartsch, E. Electrophoresis of model colloidal spheres in low salt aqueous suspension. J. Phys. Condens. Matter 2004, 16, S4039–S4050. [Google Scholar] [CrossRef]
- Ohshima, H. Electrophoretic mobility of soft particles. J. Colloid Interface Sci. 1994, 163, 474–483. [Google Scholar] [CrossRef]
- Ohshima, H. Electrophoretic mobility of a spherical colloidal particle in a salt-free medium. J. Colloid Interface Sci. 2002, 248, 499–503. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Dynamic electrophoretic mobility of spherical colloidal particles in a salt-free medium. J. Colloid Interface Sci. 2003, 265, 422–427. [Google Scholar] [CrossRef]
- Ohshima, H. Electrokinetic phenomena in a dilute suspension of spherical colloidal particles in a salt-free medium. Colloids Surf. A Physicochem. Eng. Asp. 2003, 222, 207–211. [Google Scholar] [CrossRef]
- Dukhin, S.S.; Zimmermann, R.; Werner, C. Electrokinetic fingerprinting of grafted polyelectrolyte layers—A theoretical approach. Adv. Colloid Interface Sci. 2006, 122, 93–105. [Google Scholar] [CrossRef]
- Duval, J.F.L.; Ohshima, H. Electrophoresis of diffuse soft particles. Langmuir 2006, 22, 3533–3546. [Google Scholar] [CrossRef]
- Ohshima, H. Electrokinetics of soft particles. Colloid Polym. Sci. 2007, 285, 1411–1421. [Google Scholar] [CrossRef]
- Arroyo, F.J.; Carrique, F.; Ruiz-Reina, E.; Delgado, A.V. Double layer polarization in “realistic” aqueous salt-free suspensions. Colloids Surf. A Physicochem. Eng. Asp. 2011, 376, 14–20. [Google Scholar] [CrossRef]
- Roa, R.; Carrique, F.; Ruiz-Reina, E. Electric double layer for spherical particles in salt-free concentrated suspensions including ion size effects. Phys. Chem. Chem. Phys. 2011, 13, 3960–3968. [Google Scholar] [CrossRef] [Green Version]
- Vissers, T.; Imhof, A.; Carrique, F.; Delgado, A.V.; van Blaaderen, A. Electrophoresis of concentrated colloidal dispersions in low-polar solvents. J. Colloid Interface Sci. 2011, 361, 443–455. [Google Scholar] [CrossRef] [PubMed]
- Roa, R.; Carrique, F.; Ruiz-Reina, E. Ion size effects on the electrokinetics of salt-free concentrated suspensions in ac fields. J. Colloid Interface Sci. 2012, 387, 153–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delgado, A.V.; Carrique, F.; Roa, R.; Ruiz-Reina, E. Recent developments in electrokinetics of salt-free concentrated suspensions. Curr. Opin. Colloid Interface Sci. 2016, 24, 32–43. [Google Scholar] [CrossRef]
- Lyklema, J. Fundamentals of Interface and Colloid Science; Academic Press: London, UK, 1995; Volume II. [Google Scholar]
- Ahualli, S.; Jimenez, M.L.; Carrique, F.; Delgado, A.V. AC Electrokinetics of Concentrated Suspensions of Soft Particles. Langmuir 2009, 25, 1986–1997. [Google Scholar] [CrossRef] [PubMed]
- Kuwabara, S. The forces experienced by randomly distributed parellel circular cylinders or spheres in a viscous flow at small reynolds numbers. J. Phys. Soc. Jpn. 1959, 14, 527–532. [Google Scholar] [CrossRef]
- Ohshima, H. Dynamic electrophoretic mobility of spherical colloidal particles in concentrated suspensions. J. Colloid Interface Sci. 1997, 195, 137–148. [Google Scholar] [CrossRef]
- Carrique, F.; Ruiz-Reina, E.; Roa, R.; Arroyo, F.J.; Delgado, A.V. General electrokinetic model for concentrated suspensions in aqueous electrolyte solutions: Electrophoretic mobility and electrical conductivity in static electric fields. J. Colloid Interface Sci. 2015, 455, 46–54. [Google Scholar] [CrossRef]
- Ahualli, S.; Gonzalez, M.A.; Delgado, A.V.; Jimenez, M.L. Dynamic electrophoretic mobility and electric permittivity of concentrated suspensions of plate-like gibbsite particles. J. Colloid Interface Sci. 2017, 502, 112–121. [Google Scholar] [CrossRef]
- Ahualli, S.; Delgado, A.; Miklavcic, S.J.; White, L.R. Dynamic electrophoretic mobility of concentrated dispersions of spherical colloidal particles. On the consistent use of the cell model. Langmuir 2006, 22, 7041–7051. [Google Scholar] [CrossRef]
- Tirado, M.C.; Arroyo, F.J.; Delgado, A.V.; Grosse, C. Measurement of the low-frequency dielectric properties of colloidal suspensions: Comparison between different methods. J. Colloid Interface Sci. 2000, 227, 141–146. [Google Scholar] [CrossRef]
- Jimenez, M.L.; Arroyo, F.J.; van Turnhout, J.; Delgado, A.V. Analysis of the dielectric permittivity of suspensions by means of the logarithmic derivative of its real part. J. Colloid Interface Sci. 2002, 249, 327–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chassagne, C.; Dubois, E.; Jimenez, M.L.; van der Ploeg, J.P.M.; van Turnhout, J. Compensating for Electrode Polarization in Dielectric Spectroscopy Stuides of Colloidal Suspensions: Theoretical Assessment of Existing Methods. Front. Chem. 2016, 4, 30. [Google Scholar] [CrossRef] [PubMed]
- Shilov, V.N.; Delgado, A.V.; Gonzalez-Caballero, E.; Horno, J.; Lopez-Garcia, J.J.; Grosse, C. Polarization of the electrical double layer. Time evolution after application of an electric field. J. Colloid Interface Sci. 2000, 232, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Dukhin, S.S.; Shilov, V.N. Dielectric Phenomena and the Double Layer in Disperse Systems and Polyelectrolytes; Keter Publishing: Jerusalem, Israel, 1974. [Google Scholar]
- Ohshima, H. Electrical phenomena in a suspension of soft particles. Soft Matter 2012, 8, 3511–3514. [Google Scholar] [CrossRef]
- Ohshima, H. Electrokinetic phenomena of soft particles. Curr. Opin. Colloid Interface Sci. 2013, 18, 73–82. [Google Scholar] [CrossRef]
- Hunter, R.J. Foundations of Colloid Science; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Arroyo, F.J.; Carrique, F.; Bellini, T.; Delgado, A.V. Dielectric dispersion of colloidal suspensions in the presence of stern layer conductance: Particle size effects. J. Colloid Interface Sci. 1999, 210, 194–199. [Google Scholar] [CrossRef]
- Carrique, F.; Arroyo, F.J.; Delgado, A.V. Electrokinetics of concentrated suspensions of spherical colloidal particles with surface conductance, arbitrary zeta potential, and double-layer thickness in static electric fields. J. Colloid Interface Sci. 2002, 252, 126–137. [Google Scholar] [CrossRef] [Green Version]
- Jimenez, M.L.; Delgado, A.V.; Ahualli, S.; Hoffmann, M.; Wittemanb, A.; Ballauff, M. Giant permittivity and dynamic mobility observed for spherical polyelectrolyte brushes. Soft Matter 2011, 7, 3758–3762. [Google Scholar] [CrossRef] [Green Version]












| Particle | Diameter (±S.D.) (nm) |
|---|---|
| Bare PS | 1000 ± 60 |
| PS/PDADMAC (+) | 1060 ± 60 |
| PS/PDADMAC/PSS (+/−) | 1240 ± 60 |
| PS/PDADMAC/PSS/PDADMAC (+/−/+) | 1060 ± 100 |
| PS/PDADMAC/PEO/PDADMAC (+/0/+) | 1120 ± 100 |
| Particle | Layer Thickness (nm) | Layer Charge (C/m3) | |
|---|---|---|---|
| PS/PDADMAC (+) | 40 | 7 × 105 | 10 |
| PS/PDADMAC/PSS (+/−) | 50/50 | 1 × 105/−7 × 105 | 10/35 |
| PS/PDADMAC/PSS/PDADMAC (+/−/+) | 50/50/40 | 1 × 105/−1 × 105/7 × 105 | 10/35/25 |
| PS/PDADMAC/PEO/PDADMAC (+/0/+) | 40/2/10 | 7 × 105/0/7 × 105 | 30/35/30 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahualli, S.; Bermúdez, S.; Carrique, F.; Jiménez, M.L.; Delgado, Á.V. AC Electrokinetics of Salt-Free Multilayered Polymer-Grafted Particles. Polymers 2020, 12, 2097. https://doi.org/10.3390/polym12092097
Ahualli S, Bermúdez S, Carrique F, Jiménez ML, Delgado ÁV. AC Electrokinetics of Salt-Free Multilayered Polymer-Grafted Particles. Polymers. 2020; 12(9):2097. https://doi.org/10.3390/polym12092097
Chicago/Turabian StyleAhualli, Silvia, Sara Bermúdez, Félix Carrique, María L. Jiménez, and Ángel V. Delgado. 2020. "AC Electrokinetics of Salt-Free Multilayered Polymer-Grafted Particles" Polymers 12, no. 9: 2097. https://doi.org/10.3390/polym12092097
APA StyleAhualli, S., Bermúdez, S., Carrique, F., Jiménez, M. L., & Delgado, Á. V. (2020). AC Electrokinetics of Salt-Free Multilayered Polymer-Grafted Particles. Polymers, 12(9), 2097. https://doi.org/10.3390/polym12092097