Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density
Abstract
:1. Introduction
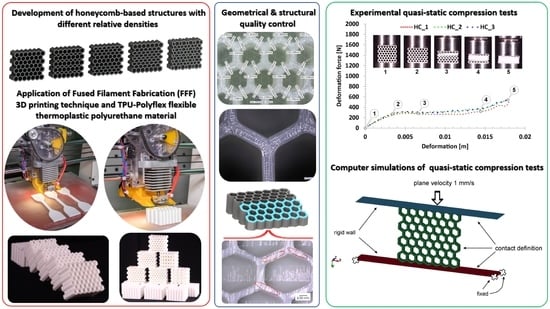
2. Development and Fabrication of Structural Specimens
3. Structural and Geometrical Quality Control
4. Determination of Mechanical Properties of the TPU Material
5. Experimental Investigations of Mechanical Properties of the Structural Specimens
6. Numerical Investigations of Mechanical Properties of Structural Specimens
7. Conclusions
- -
- Fused filament fabrication is a cost-effective 3D printing process that allows objects to be fabricated using specific filaments such as thermoplastic polyurethane (TPU 95) with unique mechanical properties. Nevertheless, the material proposed by the authors requires a direct-type filament feeding mechanism and it is recommended to conduct further technological studies in order to define the appropriate 3D printing parameters, which guarantee a structural and geometric quality of the manufactured objects.
- -
- The conducted characterisation of the mechanical properties of the TPU 95 material allows to confirm that it exhibits hyperelastic properties with a high deformation range. For this reason, it is necessary to use a suitable constitutive material model in computer simulations.
- -
- The experimental compression tests have shown a linear relationship between the relative density of the applied topology and the deformation energy value. Specimens with gradually changing topologies showed a higher value of the deformation energy compared to the reference honeycomb structure.
- -
- By analysing the history plots of the deformation processes of the specimens, a lack of crack damage mechanism can be observed due to the high flexibility of the applied TPU 95 filament. The main mechanisms occurring during the compression test were buckling and bending.
- -
- The proposed numerical approach to the investigations made it possible to predict the structural deformation process. The results obtained agree well with the data recorded during the experimental tests.
- -
- The adopted simplified rubber material constitutive model, defined on the basis of experimental compression and tensile tests, enables correct reproduction of the mechanical response of the structural specimens made with the TPU 95 filament.
- -
- The developed models will be used in further numerical investigations conducted under dynamic load conditions.
- -
- Planned investigations taking into account dynamic loading conditions will be carried out experimentally as well as numerically. The experimental approach will be performed with the Split Hopkinson Pressure Bar stand implementation in a direct impact configuration. The numerical approach will allow for verification of the proposed numerical model. A good correlation between results enables us to perform further optimisation studies.
- -
- Obtained results of the dynamic tests offer the chance for evaluation of developed structures as well as highly flexible Polyflex TPU 95a material in terms of energy absorption.
Author Contributions
Funding
Conflicts of Interest
References
- Li, N.; Huang, S.; Zhang, G.; Qin, R.; Liu, W.; Xiong, H.; Shi, G.; Blackburn, J. Progress in additive manufacturing on new materials: A review. J. Mater. Sci. Technol. 2019, 35, 242–269. [Google Scholar] [CrossRef]
- Strong, D.; Kay, M.; Conner, B.; Wakefield, T.; Manogharan, G. Hybrid manufacturing—Integrating traditional manufacturers with additive manufacturing (AM) supply chain. Addit. Manuf. 2018, 21, 159–173. [Google Scholar] [CrossRef]
- Prakash, K.S.; Nancharaih, T.; Rao, V.S. Additive manufacturing techniques in manufacturing —An Overview. Mater. Today Proc. 2018, 5, 3873–3882. [Google Scholar] [CrossRef]
- Murr, L. Frontiers of 3D printing/additive manufacturing: From human organs to aircraft fabrication. J. Mater. Sci. Technol. 2016, 32, 987–995. [Google Scholar] [CrossRef]
- Ngo, T.; Kashani, A.; Imbalzano, G.; Nguyen, Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Craveiro, F.; Duarte, J.P.; Bartolo, P.; Bartolo, P. Additive manufacturing as an enabling technology for digital construction: A perspective on Construction 4.0. Autom. Constr. 2019, 103, 251–267. [Google Scholar] [CrossRef]
- Du Plessis, A.; Broeckhoven, C.; Yadroitsava, I.; Yadroitsev, I.; Hands, C.H.; Kunju, R.; Bhate, D. Beautiful and functional: A review of biomimetic design in additive manufacturing. Addit. Manuf. 2019, 27, 408–427. [Google Scholar] [CrossRef]
- Dizon, J.R.C.; Espera, A.H.; Chen, Q.; Advincula, R.C. Mechanical characterization of 3D-printed polymers. Addit. Manuf. 2018, 20, 44–67. [Google Scholar] [CrossRef]
- Kumar, S.; Czekanski, A. Roadmap to sustainable plastic additive manufacturing. Mater. Today Commun. 2018, 15, 109–113. [Google Scholar] [CrossRef]
- Yuan, S.; Shen, F.; Chua, C.K.; Zhou, K. Polymeric composites for powder-based additive manufacturing: Materials and applications. Prog. Polym. Sci. 2019, 91, 141–168. [Google Scholar] [CrossRef]
- Azarov, A.V.; Antonov, F.K.; Golubev, M.; Khaziev, A.; Ushanov, S.A. Composite 3D printing for the small size unmanned aerial vehicle structure. Compos. Part B Eng. 2019, 169, 157–163. [Google Scholar] [CrossRef]
- Valino, A.D.; Dizon, J.R.C.; Espera, A.H., Jr.; Chen, Q.; Messman, J.; Advincula, R.C. Advances in 3D printing of thermoplastic polymer composites and nanocomposites. Prog. Polym. Sci. 2019, 98, 101162. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Khosravani, M.R.; Kaynak, A. Fracture resistance analysis of 3D-printed polymers. Polymers 2020, 12, 302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zolfagharian, A.; Kaynak, A.; Bodaghi, M.; Kouzani, A.Z.; Gharaie, D.W.P.; Nahavandi, S. Control-based 4D printing: Adaptive 4D-printed systems. Appl. Sci. 2020, 10, 3020. [Google Scholar] [CrossRef]
- Kluczyński, J.; Śnieżek, L.; Kravcov, A.; Grzelak, K.; Svoboda, P.; Szachogłuchowicz, I.; Franek, O.; Morozov, N.; Torzewski, J.; Kubeček, P. The examination of restrained joints created in the process of multi-material FFF additive manufacturing technology. Materials 2020, 13, 903. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Tian, X.; Huang, L.; Li, D.; Malakhov, A.V.; Polilov, A.N. Programmable morphing composites with embedded continuous fibers by 4D printing. Mater. Des. 2018, 155, 404–413. [Google Scholar] [CrossRef]
- Mitchell, A.; Lafont, U.; Hołyńska, M.; Semprimoschnig, C. Additive manufacturing—A review of 4D printing and future applications. Addit. Manuf. 2018, 24, 606–626. [Google Scholar] [CrossRef]
- Rayate, A.; Jain, P.K. A Review on 4D printing material composites and their applications. Mater. Today Proc. 2018, 5, 20474–20484. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-based 3D printing of polymer and associated composite: A review on mechanical properties, defects and treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef]
- Kashyap, D.; Kumar, P.K.; Kanagaraj, S. 4D printed porous radiopaque shape memory polyurethane for endovascular embolization. Addit. Manuf. 2018, 24, 687–695. [Google Scholar] [CrossRef]
- Haryńska, A.; Carayon, I.; Kucińska-Lipka, J.; Janik, H. Fabrication and characterization of flexible medical-grade TPU filament for fused deposition modeling 3DP technology. Polymers 2018, 10, 1304. [Google Scholar] [CrossRef] [Green Version]
- Blok, L.; Longana, M.L.; Yu, H.; Woods, B. An investigation into 3D printing of fibre reinforced thermoplastic composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar] [CrossRef]
- Sang, L.; Han, S.; Li, Z.; Yang, X.; Hou, W. Development of short basalt fiber reinforced polylactide composites and their feasible evaluation for 3D printing applications. Compos. Part B Eng. 2019, 164, 629–639. [Google Scholar] [CrossRef]
- Soltani, A.; Noroozi, R.; Bodaghi, M.; Zolfagharian, A.; Hedayati, R. 3D printing on-water sports boards with bio-inspired core designs. Polymers 2020, 12, 250. [Google Scholar] [CrossRef] [Green Version]
- Herzberger, J.; Sirrine, J.M.; Williams, C.B.; Long, T.E. Polymer design for 3D printing elastomers: Recent advances in structure, properties, and printing. Prog. Polym. Sci. 2019, 97, 101144. [Google Scholar] [CrossRef]
- Robinson, M.; Soe, S.P.; Johnston, R.; Adams, R.; Hanna, B.; Burek, R.; McShane, G.; Celeghini, R.; Alves, M.; Theobald, P. Mechanical characterisation of additively manufactured elastomeric structures for variable strain rate applications. Addit. Manuf. 2019, 27, 398–407. [Google Scholar] [CrossRef]
- Antolak-Dudka, A.; Płatek, P.; Durejko, T.; Baranowski, P.; Małachowski, J.; Sarzyński, M.; Czujko, T. Static and dynamic loading behavior of Ti6Al4V Honeycomb Structures Manufactured by Laser Engineered Net Shaping (LENSTM) technology. Materials 2019, 12, 1225. [Google Scholar] [CrossRef] [Green Version]
- Delcuse, L.; Bahi, S.; Gunputh, U.; Rusinek, A.; Wood, P.; Miguelez, M. Effect of powder bed fusion laser melting process parameters, build orientation and strut thickness on porosity, accuracy and tensile properties of an auxetic structure in IN718 alloy. Addit. Manuf. 2020, 36, 101339. [Google Scholar] [CrossRef]
- Stanczak, M.; Fras, T.; Blanc, L.; Pawlowski, P.; Rusinek, A. Blast-induced compression of a thin-walled aluminum honeycomb structure—Experiment and modeling. Metals 2019, 9, 1350. [Google Scholar] [CrossRef] [Green Version]
- Kurzawa, A.; Pyka, D.; Jamroziak, K.; Bajkowski, M.; Bocian, M.; Magier, M.; Koch, J. Assessment of the impact resistance of a composite material with EN AW-7075 matrix reinforced with α-Al2O3 particles using a 7.62 × 39 mm projectile. Materials 2020, 13, 769. [Google Scholar] [CrossRef] [Green Version]
- Jamroziak, K.; Bajkowski, M.; Bocian, M.; Polak, S.; Magier, M.; Kosobudzki, M.; Stepien, R. Ballistic head protection in the light of injury criteria in the case of the Wz.93 combat helmet. Appl. Sci. 2019, 9, 2702. [Google Scholar] [CrossRef] [Green Version]
- Arkusz, K.; Klekiel, T.; Slawinski, G.; Będziński, R. Influence of energy absorbers on Malgaigne fracture mechanism in lumbar-pelvic system under vertical impact load. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 313–323. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Le Barbenchon, L.; Bednarcyk, B.A.; Scarpa, F.; Chen, Y. Bioinspired multilayered cellular composites with enhanced energy absorption and shape recovery. Addit. Manuf. 2020, 36, 101430. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M.; Aghdam, M.; Zadpoor, A.A. Mechanical properties of additively manufactured thick honeycombs. Materials 2016, 9, 613. [Google Scholar] [CrossRef]
- Lopez, D.M.B.; Ahmad, R. Tensile mechanical behaviour of multi-polymer sandwich structures via fused deposition modelling. Polymers 2020, 12, 651. [Google Scholar] [CrossRef] [Green Version]
- Velasco-Hogan, A.; Xu, J.; Meyers, M.A. Additive manufacturing as a method to design and optimize bioinspired structures. Adv. Mater. 2018, 30. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Q.; Scarpa, F.; Liu, Y.; Leng, J. In-plane elasticity of a novel auxetic honeycomb design. Compos. Part B Eng. 2017, 110, 72–82. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Gong, X.; Zhang, Q.; Scarpa, F.; Liu, Y.; Leng, J. In-plane mechanics of a novel zero Poisson’s ratio honeycomb core. Compos. Part B Eng. 2016, 89, 67–76. [Google Scholar] [CrossRef] [Green Version]
- Boldrin, L.; Hummel, S.; Scarpa, F.; Di Maio, D.; Lira, C.; Ruzzene, M.; Remillat, C.; Lim, T.-C.; Rajasekaran, R.; Patsias, S. Dynamic behaviour of auxetic gradient composite hexagonal honeycombs. Compos. Struct. 2016, 149, 114–124. [Google Scholar] [CrossRef] [Green Version]
- Zaharia, S.M.; Enescu, L.A.; Pop, M.A. Mechanical Performances of lightweight sandwich structures produced by material extrusion-based additive manufacturing. Polymers 2020, 12, 1740. [Google Scholar] [CrossRef]
- Bates, S.R.; Farrow, I.R.; Trask, R.S. Compressive behaviour of 3D printed thermoplastic polyurethane honeycombs with graded densities. Mater. Des. 2019, 162, 130–142. [Google Scholar] [CrossRef]
- Kucewicz, M.; Baranowski, P.; Małachowski, J.; Popławski, A.; Płatek, P. Modelling, and characterization of 3D printed cellular structures. Mater. Des. 2018, 142, 177–189. [Google Scholar] [CrossRef]
- Kucewicz, M.; Baranowski, P.; Małachowski, J. A method of failure modeling for 3D printed cellular structures. Mater. Des. 2019, 174, 107802. [Google Scholar] [CrossRef]
- Yang, C.; Vora, H.D.; Chang, Y. Behavior of auxetic structures under compression and impact forces. Smart Mater. Struct. 2018, 27, 025012. [Google Scholar] [CrossRef]
- Qi, C.; Jiang, F.; Yu, C.; Yang, S. In-plane crushing response of tetra-chiral honeycombs. Int. J. Impact Eng. 2019, 130, 247–265. [Google Scholar] [CrossRef]
- Tabacu, S.; Ducu, C. Experimental testing and numerical analysis of FDM multi-cell inserts and hybrid structures. Thin-Walled Struct. 2018, 129, 197–212. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.; Hu, G.; Liao, W.-H. Large deformations of soft metamaterials fabricated by 3D printing. Mater. Des. 2017, 131, 81–91. [Google Scholar] [CrossRef]
- Hallquist, J. LS-DYNA® Theory Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006; ISBN 9254492507. [Google Scholar]
- Kucewicz, M.; Baranowski, P.; Stankiewicz, M.; Konarzewski, M.; Płatek, P.; Małachowski, J. Modelling and testing of 3D printed cellular structures under quasi-static and dynamic conditions. Thin-Walled Struct. 2019, 145, 106385. [Google Scholar] [CrossRef]
- Baranowski, P.; Płatek, P.; Antolak-Dudka, A.; Sarzyński, M.; Kucewicz, M.; Durejko, T.; Małachowski, J.; Janiszewski, J.; Czujko, T. Deformation of honeycomb cellular structures manufactured with Laser Engineered Net Shaping (LENS) technology under quasi-static loading: Experimental testing and simulation. Addit. Manuf. 2019, 25, 307–316. [Google Scholar] [CrossRef]
- Hanssen, A.; Hopperstad, O.; Langseth, M.; Ilstad, H. Validation of constitutive models applicable to aluminium foams. Int. J. Mech. Sci. 2002, 44, 359–406. [Google Scholar] [CrossRef]
- Baranowski, P.; Małachowski, J.; Mazurkiewicz, Ł. Numerical and experimental testing of vehicle tyre under impulse loading conditions. Int. J. Mech. Sci. 2016, 106, 346–356. [Google Scholar] [CrossRef]
- Baranowski, P.; Małachowski, J.; Janiszewski, J.; Wekezer, J. Detailed tyre FE modelling with multistage validation for dynamic analysis. Mater. Des. 2016, 96, 68–79. [Google Scholar] [CrossRef]
- Freidenberg, A.; Lee, C.; Durant, B.; Nesterenko, V.; Stewart, L.; Hegemier, G. Characterization of the Blast Simulator elastomer material using a pseudo-elastic rubber model. Int. J. Impact Eng. 2013, 60, 58–66. [Google Scholar] [CrossRef]
- Karagiozova, D.; Mines, R. Impact of aircraft rubber tyre fragments on aluminium alloy plates: II—Numerical simulation using LS-DYNA. Int. J. Impact Eng. 2007, 34, 647–667. [Google Scholar] [CrossRef]



























| No. | Wall Thickness [mm] | Dimensions of Specimen [mm] | Theoretical Relative Density ρrel [–] |
|---|---|---|---|
| Specimen No.1 (HC) | 1.0 | 31.4 × 34.4 × 20.0 | 0.37 |
| Specimen No.2 (HCG_D) | 1.0 | 31.4 × 34.4 × 20.0 | 0.39 |
| Specimen No.3 (HCG_I) | 1.0 | 31.4 × 34.4 × 20.0 | 0.39 |
| Specimen No.4 (HCG_Ds) | 1.0 | 31.4 × 34.4 × 20.0 | 0.38 |
| Specimen No.5 (HCG_BD) | 1.0 | 31.4 × 34.4 × 20.0 | 0.42 |
| Mechanical properties | Density (ASTM D792) | Melt Index (210 °C, 1.2 kg) | Elastic Modulus (X-Y) ASTM D638 | Tensile Strength (X-Y) ASTM D638 | Elongation at Break (X-Y) ASTM D638 | Shore Hardness ASTM D2240 |
|---|---|---|---|---|---|---|
| TPU 95-Polyflex | 1.20–1.24 | 3–6 (g/10 min) | 9.4 ± 0.3 (MPa) | 29.0 ± 2.8 (MPa) | 330.1 ± 14.9 (%) | 95 A |
| Parameters Group | Nozzle Temperature (°C) | Bed Temperature (°C) | Wall Printing Speed (mm/s) | Infill Printing Speed (mm/s) | Layer Height (mm) | Line Width (mm) | Flow Ratio (%) |
|---|---|---|---|---|---|---|---|
| Parameters set No.1 | 215.0 ± 0.2 | 60.0 ± 0.1 | 6.00 | 12.00 | 0.2 | 0.4 | 145.0 |
| Parameters set No.2 | 215.0 ± 0.2 | 60.0 ± 0.1 | 6.00 | 12.00 | 0.2 | 0.4 | 125.0 |
| Parameters set No.3 | 215.0 ± 0.2 | 60.0 ± 0.1 | 12.00 | 12.00 | 0.2 | 0.4 | 100.0 |
| Set Groups | W1 [mm] | W2 [mm] | W3 [mm] | W4 [mm] | S1 [mm] | S2 [mm] | S3 [mm] | S4 [mm] | H1 [mm] | H2 [mm] | H3 [mm] | H4 [mm] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nominal Values | 0.60 | 0.80 | 1.00 | 1.2 | 0.60 | 0.80 | 1.00 | 1.2 | 0.60 | 0.80 | 1.00 | 1.2 |
| Set No.1 | 0.89 ± 0.02 | 1.06 ± 0.02 | 1.13 ± 0.03 | 1.32 ± 0.03 | 0.94 ± 0.05 | 1.12 ± 0.06 | 1.27 ± 0.04 | 1.48 ± 0.09 | 0.94 ± 0.04 | 1.11 ± 0.03 | 1.28 ± 0.03 | 1.50 ± 0.05 |
| Set No.2 | 0.80 ± 0.02 | 1.01 ± 0.02 | 1.13 ± 0.03 | 1.33 ± 0.03 | 0.75 ± 0.04 | 0.94 ± 0.04 | 1.21 ± 0.05 | 1.39 ± 0.06 | 0.73 ± 0.05 | 0.93 ± 0.06 | 1.11 ± 0.09 | 1.32 ± 0.09 |
| Set No.3 | 0.72 ± 0.02 | 0.84 ± 0.02 | 1.28 ± 0.03 | 1.36 ± 0.03 | 0.66 ± 0.02 | 0.84 ± 0.03 | 1.13 ± 0.03 | 1.31 ± 0.04 | 0.67 ± 0.02 | 0.84 ± 0.03 | 1.11 ± 0.03 | 1.38 ± 0.04 |
| Strain [-] | −0.83 | −0.78 | −0.71 | −0.69 | −0.64 | −0.43 | −0.33 | −0.23 | −0.14 | −0.09 | −0.04 | −0.03 |
| Stress [MPa] | −270.48 | −156.06 | −83.28 | −69.07 | −50.23 | −20.11 | −14.95 | −10.02 | −6.02 | −3.91 | −1.96 | −1.05 |
| Strain [-] | 0.0 | 0.04 | 0.1 | 0.23 | 0.71 | 1.45 | 2.34 | 2.67 | 2.96 | 3.24 | 3.55 | 3.81 |
| Stress [MPa] | 0.0 | 2.0 | 4.01 | 5.99 | 7.99 | 10.01 | 14.99 | 20.02 | 25.0 | 29.97 | 34.99 | 38.0 |
| RO Density | KM Linear Bulk Modulus | SGL Specimen Gauge Length | SW Specimen Width | ST Specimen Thickness |
|---|---|---|---|---|
| 1100.00 kg/m3 | 1.650 × 109 Pa | 1.00 | 1.00 | 1.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Płatek, P.; Rajkowski, K.; Cieplak, K.; Sarzyński, M.; Małachowski, J.; Woźniak, R.; Janiszewski, J. Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density. Polymers 2020, 12, 2120. https://doi.org/10.3390/polym12092120
Płatek P, Rajkowski K, Cieplak K, Sarzyński M, Małachowski J, Woźniak R, Janiszewski J. Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density. Polymers. 2020; 12(9):2120. https://doi.org/10.3390/polym12092120
Chicago/Turabian StylePłatek, Paweł, Kamil Rajkowski, Kamil Cieplak, Marcin Sarzyński, Jerzy Małachowski, Ryszard Woźniak, and Jacek Janiszewski. 2020. "Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density" Polymers 12, no. 9: 2120. https://doi.org/10.3390/polym12092120
APA StylePłatek, P., Rajkowski, K., Cieplak, K., Sarzyński, M., Małachowski, J., Woźniak, R., & Janiszewski, J. (2020). Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density. Polymers, 12(9), 2120. https://doi.org/10.3390/polym12092120