Assessing the Compressive and Impact Behavior of Plastic Safety Toe Caps through Computational Modelling
Abstract
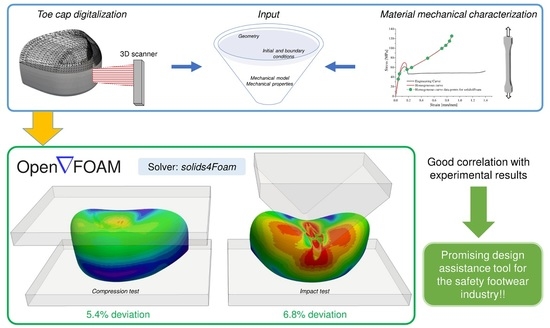
:1. Introduction
1.1. Safety Footwear
1.2. Fluid-Solid Interaction within OpenFOAM®
2. Materials and Methods
2.1. Material Characterization
2.1.1. InfraRed Spectroscopy
2.1.2. Thermal Analysis
2.1.3. Morphology
2.1.4. Mechanical Characterization
2.2. Simulation Setup
2.2.1. Toe Cap Geometry
2.2.2. Mesh Sensitivity Analysis
2.2.3. Quasi-Static Compression Test
2.2.4. Impact Test
- The base plate was defined to have a fixed zero displacement in all Cartesian directions (Fixed walls patch in Figure 4 Right);
- To constrain the striker to the y-direction, the faces with normal vector pointing into x- and z-direction were set as symmetry planes (Symmetry planes patches in Figure 4 Right);
- The contact regions were simulated with the same method and values used for the compression structural analysis (Upper and Bottom contact patches in Figure 4 Right).
- The initial velocity was imposed on the striker by using the OpenFOAM ® utility, setFields.
3. Results and Discussion
3.1. Toe Cap Material Characterization
3.2. Mesh Sensitivity Analysis
3.3. Quasi-Static Compression Test
3.4. Impact Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eurostat. Health and Safety at Work: Accidents at Work by NACE Rev. 2 Activity and Part of Body Injured. Available online: https://ec.europa.eu/eurostat/web/health/data/database## (accessed on 24 February 2020).
- ISO. Personal Protective Equipment—Safety Footwear; ISO 20345:2011(E); ISO: Geneva, Switzerland, 2011. [Google Scholar]
- ISO. Personal Protective Equipment—Protective Footwear; ISO 20346:2014; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- ISO. Personal Protective Equipment—Occupational Footwear; ISO 20347:2012; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Kwon, J.Y.; Campbell, J.T.; Myerson, M.S.; Jeng, C.L. Effect of a Steel Toe Cap on Forefoot Injury Pattern in a Cadaveric Model. Foot Ankle Int. 2011, 32, 443–447. [Google Scholar] [CrossRef] [PubMed]
- Chiou, S.S.; Turner, N.; Zwiener, J.; Weaver, D.L.; Haskell, W.E. Effect of Boot Weight and Sole Flexibility on Gait and Physiological Responses of Firefighters in Stepping Over Obstacles. Hum. Factors: J. Hum. Factors Ergon. Soc. 2012, 54, 373–386. [Google Scholar] [CrossRef]
- Abreu, M.J.; Pereira, C.S.; Mendonça, J.P.; Abreu, A.P. Design of innovative protective insoles for satefy footwear. In Proceedings of the 2017 International Conference on Engineering, Technology and Innovation (ICE/ITMC), Madeira Island, Portugal, 27–29 June 2017; pp. 231–236. [Google Scholar]
- Goldcher, A.; Acker, D. Chaussures de sécurité, de protection et de travail. EMC-Podol. 2005, 1, 12–23. [Google Scholar] [CrossRef]
- Marr, S.; Quine, S. Shoe concerns and foot problems of wearers of safety footwear. Occup. Med. 1993, 43, 73–77. [Google Scholar] [CrossRef]
- Janson, D.; Newman, S.; Dhokia, V. Safety footwear: A survey of end-users. Appl. Ergon. 2021, 92, 103333. [Google Scholar] [CrossRef]
- Wojcik, F.J. Foot Shield. U.S. Patent 1,626,489, 26 April 1927. [Google Scholar]
- Hauer, A.W. Toe Protector. U.S. Patent 2,002,662, 28 May 1935. [Google Scholar]
- Allard, A.R. Safety Shoe. U.S. Patent 2,079,237, 4 May 1937. [Google Scholar]
- Richards, W.J. Safety Show. U.S. Patent 2,836,909, 3 June 1958. [Google Scholar]
- Costa, S.L.; Mendonça, J.P.; Peixinho, N. Numerical Simulation of Quasi-Static Compression Behavior of the Toe Cap Component for Safety Footwear. Int. J. Comput. Theory Eng. 2014, 6, 285–291. [Google Scholar] [CrossRef] [Green Version]
- Frulla, C. Protective Toecap, Particularly for Safety Shoes. WO 03/037127 A1, 8 May 2003. [Google Scholar]
- Fron, F. Plastic Foot Protector. U.S. Patent 4,103,438, 1 August 1978. [Google Scholar]
- Tanaka, Y.; Hirota, M.; Ishida, T. Resin Safety Shoe Toe Cap. European Patent 1 380 221 A1, 14 January 2004. [Google Scholar]
- Yang, C.C.; Duhovic, M.; Lin, R.; Bhattacharyya, D. Finite element modelling and analysis of composites toecaps. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Auckland, New Zealand, 8–9 April 2009; Volume 4, pp. 1–6. [Google Scholar] [CrossRef]
- Erden, S.; Ertekin, M. Mechanical Evaluation of a Composite Overshoe Protector. Tekst. Ve Konfeks. 2017, 27, 414–420. [Google Scholar]
- Lee, S.M.; Lim, T.S.; Gil Lee, D. Damage tolerance of composite toecap. Compos. Struct. 2005, 67, 167–174. [Google Scholar] [CrossRef]
- Dykeman, J.L. Protective Toe Cap for Footwear. U.S. Patent 4,735,003, 5 April 1988. [Google Scholar]
- Costa, S.L.; Silva, J.; Peixinho, N.; Mendonça, J.P. Advanced Metallic Solution for Toe Cap Component. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013; pp. 1–9. [Google Scholar]
- Bartkowiak, G.; Baszczyński, K.; Bogdan, A.; Brochocka, A.; Dąbrowska, A.; Hrynyk, R.; Irzmańska, E.; Koradecka, D.; Kozłowski, E.; Majchrzycka, K.; et al. Use of Personal Protective Equipment: 25. In Handbook of Human Factors and Ergonomics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; pp. 668–684. [Google Scholar]
- Yang, C.-C. Development of High Strength Composite Toecaps Using LS-DYNA. Master’s Thesis, Centre for Advanced Composite Materials/Department of Mechanical Engineering, The University of Auckland, Auckland, New Zealand, 2010. [Google Scholar]
- Jankauskaitė, V.; Žukas, T.; Žukienė, K.; Malcius, M. Low-weight Impact Behaviour of Carbon Fibre Reinforced Methyl Methacrylate Nanocomposites. Mater. Sci. 2015, 21, 232–237. [Google Scholar] [CrossRef]
- Costa, S.; Peixinho, N.; Mendonça, J. Design and Testing of a New Metallic Solution for Toecap Component on Safety Footwear. Appl. Mech. Mater. 2010, 44–47, 1460–1464. [Google Scholar] [CrossRef]
- Peixinho, N.; Costa, S.; Mendonça, J. Impact Behaviour of Safety Shoe High Strength Steel Parts. Eng. Trans. 2018, 66, 175–185. [Google Scholar]
- Costa, S.L.; Mendonça, J.P.; Peixinho, N. Study on the impact behaviour of a new safety toe cap model made of ultra-high-strength steels. Mater. Des. 2016, 91, 143–154. [Google Scholar] [CrossRef]
- Soares, R.C.F. Simulação Numérica do Comportamento ao Impacto de Componentes para Calçado de Segurança. Master’s Thesis, Departamento de Engenharia Mecânica, Universidade do Minho, Braga, Portugal, 2015. [Google Scholar]
- Dirksen, N.; Deters, P.; Peikenkamp, K. Numerical simulation of compression testing according to DIN EN 12568 of steel toe caps for safety footwear. Footwear Sci. 2019, 11, S182–S184. [Google Scholar] [CrossRef]
- Hu, K.; Chen, G.; Zhou, C.; Reniers, G.; Qi, S.; Zhou, Z. Dynamic response of a large vertical tank impacted by blast fragments from chemical equipment. Saf. Sci. 2020, 130, 104863. [Google Scholar] [CrossRef]
- Masoumi, A.; Shojaeefard, M.H.; Najibi, A. Comparison of steel, aluminum and composite bonnet in terms of pedestrian head impact. Saf. Sci. 2011, 49, 1371–1380. [Google Scholar] [CrossRef]
- Sun, J.; Fan, H.; Wei, C.; Jiang, T.; Zhao, Y. Numerical simulation on foam ceramic blasting block device under the action of explosion transform. Saf. Sci. 2012, 50, 588–592. [Google Scholar] [CrossRef]
- Schamp, E.; Shaw, P.; Vernon, J.; Kantor, E.; Bertram, H. In-Depth Assessment of the Situation of the European Footwear Sector and Prospects for Its Future Development: Task 7: Synthesis Report—Study; Revised Final Report; Risk & Policy Analysts Ltd, Publications Office of the European Union: Luxembourg, 2012; Available online: https://op.europa.eu/en/publication-detail/-/publication/daf8fc79-394f-4157-996d-829b63b916dc (accessed on 21 February 2020).
- Cardiff, P.; Karač, A.; De Jaeger, P.; Jasak, H.; Nagy, J.; Ivanković, A.; Tuković, Ž. An open-source finite volume toolbox for solid mechanics and fluid-solid interaction simulations. arXiv 2018, arXiv:1808.10736. [Google Scholar]
- Foot and Leg Protectors—Requirements and Test Methods for Toecaps and Penetration Resistant Inserts; EN 12568:2010; European Committee for Standardization: Brussels, Belgium, 2010.
- Foam-Extend. Available online: https://sourceforge.net/projects/foam-extend/ (accessed on 21 October 2020).
- Tuković, Ž.; Karač, A.; Cardiff, P.; Jasak, H.; Ivanković, A. OpenFOAM Finite Volume Solver for Fluid-Solid Interaction. Trans. FAMENA 2018, 42, 1–31. [Google Scholar] [CrossRef]
- Tang, T.; Hededal, O.; Cardiff, P. On finite volume method implementation of poro-elasto-plasticity soil model. Int. J. Numer. Anal. Methods Géoméch. 2015, 39, 1410–1430. [Google Scholar] [CrossRef]
- Cardiff, P.; Tuković, Ž.; De Jaeger, P.; Clancy, M.; Ivanković, A. A Lagrangian cell-centred finite volume method for metal forming simulation. Int. J. Numer. Methods Eng. 2017, 109, 1777–1803. [Google Scholar] [CrossRef] [Green Version]
- Cardiff, P.; Karač, A.; Ivanković, A. A large strain finite volume method for orthotropic bodies with general material orientations. Comput. Methods Appl. Mech. Eng. 2014, 268, 318–335. [Google Scholar] [CrossRef]
- Cardiff, P.; Tukovic, Z.; Jasak, H.; Ivankovic, A. A block-coupled Finite Volume methodology for linear elasticity and unstructured meshes. Comput. Struct. 2016, 175, 100–122. [Google Scholar] [CrossRef] [Green Version]
- Tuković, Ž.; Bukač, M.; Cardiff, P.; Jasak, H.; Ivanković, A. Added Mass Partitioned Fluid–Structure Interaction Solver Based on a Robin Boundary Condition for Pressure. In OpenFOAM®: Selected Papers of the 11th Workshop; Nóbrega, J.M., Jasak, H., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1–22. [Google Scholar]
- Polanco-Loria, M.; Clausen, A.H.; Berstad, T.; Hopperstad, O.S. Constitutive model for thermoplastics with structural applications. Int. J. Impact Eng. 2010, 37, 1207–1219. [Google Scholar] [CrossRef]
- Manas, P.; Vrana, R.; Hejmal, Z.; Dubec, B. Determination of the Material Properties of Recycled Rubber for Explicit FEM Simulation. Key Eng. Mater. 2017, 755, 1–7. [Google Scholar] [CrossRef]
- Owaid, H.S. Modeling of A Head-Neck Assembly Drop Tower Impact Test Using Abaqus. Master’s Thesis, The University of Maine, Orono, ME, USA, 2009. [Google Scholar]
- Wan, X.; Liu, X.; Shan, Y.; Jiang, E.; Yuan, H. Numerical and experimental investigation on the effect of tire on the 13° impact test of automotive wheel. Adv. Eng. Softw. 2019, 133, 20–27. [Google Scholar] [CrossRef]
- Waxman, R.; Guven, I. Implementation of a Neo-Hookean Material Model in State-Based Peridynamics to Represent Nylon Bead Behavior during High-Speed Impact. In Proceedings of the AIAA SciTech Forum, AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Deblieck, R.; Remerie, K.; Fonteyne, W.V.D.; Boerakker, M. A Morphology-Based Model to Describe the Low-Temperature Impact Behaviour of Rubber-Toughened Polypropylene. Polymers 2021, 13, 2218. [Google Scholar] [CrossRef] [PubMed]
- cfMesh. Available online: https://sourceforge.net/projects/cfmesh/ (accessed on 23 October 2020).
- Fabritius, B.; Tabor, G. Improving the quality of finite volume meshes through genetic optimisation. Eng. Comput. 2016, 32, 425–440. [Google Scholar] [CrossRef] [Green Version]
- Norris, S.E. Finite Volume Methods for Non-Orthogonal Meshes. In A Parallel Navier Stokes Solver for Natural Convection and Free Surface Flow; University of Sydney: Sydney, Australia, 2000; Chapter 5; Available online: http://hdl.handle.net/2123/376 (accessed on 30 October 2020).
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College London, University of London, London, UK, 1996. Available online: http://hdl.handle.net/10044/1/8335 (accessed on 28 October 2020).
- ISO. Personal Protective Equipment—Test Methods for Footwear; ISO 20344:2011 (E); ISO: Geneva, Switzerland, 2011. [Google Scholar]
- Lee, J.; Xu, G.; Liang, H. Experimental and numerical analysis of friction and wear behavior of polycarbonate. Wear 2001, 251, 1541–1556. [Google Scholar] [CrossRef]
- PDL Staff. Fatigue and Tribological Properties of Plastics and Elastomers; Plastics Design Library: Morris, NY, USA, 1995. [Google Scholar]
- Abbate, M.; Martuscelli, E.; Musto, P.; Ragosta, G.; Scarinzi, G. Toughening of a highly cross-linked epoxy resin by reactive blending with bisphenol A polycarbonate. I. FTIR spectroscopy. J. Polym. Sci. Part B Polym. Phys. 1994, 32, 395–408. [Google Scholar] [CrossRef]
- Delpech, M.C.; Coutinho, F.M.; Habibe, M.E.S. Bisphenol A-based polycarbonates: Characterization of commercial samples. Polym. Test. 2002, 21, 155–161. [Google Scholar] [CrossRef]
- ParaView—v5.6.2. Available online: https://www.paraview.org/ (accessed on 23 October 2020).
- Kropidłowska, P.; Irzmańska, E.; Zgórniak, P.; Byczkowska, P. Evaluation of the mechanical strength and protective properties of polycarbonate toecaps subjected to repeated impacts simulating workplace conditions. Int. J. Occup. Saf. Ergon. 2021, 27, 698–707. [Google Scholar] [CrossRef] [PubMed]





















| Category of Footwear | |||
|---|---|---|---|
| Toe Cap Requirements | Safety ISO 20345 | Protective ISO 20346 | Occupational ISO 20347 |
| Impact energy (J) | 200 | 100 | - |
| Compression load (kN) | 15 | 10 | - |
| Toe cap size | ≤5 | 6 | 7 | 8 | 9 | ≥10 |
| Toe cap clearance (mm) | 19.5 | 20.0 | 20.5 | 21.0 | 21.5 | 22.0 |
| Shoe size | ≤36 | 37–38 | 39–40 | 41–42 | 43–44 | ≥45 |
| Toe cap clearance inside the shoe (mm) | 12.5 | 13.0 | 13.5 | 14.0 | 14.5 | 15.0 |
| Mesh Properties/Cell Type (Number/%) | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|
| cell average size (mm) | 1.7 | 1.1 | 0.65 | 0.449 | 0.31 |
| Total number of cells | 25,216 | 74,272 | 227,541 | 670,640 | 1,973,199 |
| Max. non-orthogonality | 64.16 | 67.75 | 61.40 | 57.11 | 58.69 |
| Average non-orthogonality | 19.28 | 15.6 | 3.98 | 3.15 | 2.61 |
| Max. skewness | 1.12 | 0.99 | 1.22 | 1.86 | 0.99 |
| Average skewness | 0.29 | 0.22 | 0.09 | 0.07 | 0.05 |
| Hexahedron | 24,598 (97.55%) | 73,243 (98.61%) | 226,626 (99.60%) | 669,560 (99.84%) | 1,971,480 (99.91%) |
| Prism | 56 (0.22%) | 74 (0.10%) | 98 (0.04%) | 136 (0.02%) | 206 (0.01%) |
| Pyramid | 258 (1.02%) | 409 (0.55%) | 383 (0.17%) | 472 (0.07%) | 715 (0.04%) |
| Tetrahedron | 304 (1.21%) | 546 (0.74%) | 434 (0.19%) | 472 (0.07%) | 798 (0.04%) |
| Discretization Schemes | Solver Control Parameters | ||
|---|---|---|---|
| d2dt2 | Euler | D, DD and sigmaHyd | |
| Time | Euler | ||
| Gradient | Least squares | Solver | PCG |
| Divergence | Gauss Linear | Preconditioner | FDIC |
| Laplacian | Gauss Linear corrected | Tolerance | 1 × 10−7 |
| laplacian(DD,D) | Relative tolerance | 0.1 | |
| laplacian(DDD,DD) | |||
| Surface normal gradient | New skew corrected 1 | ||
| snGrad(D) | |||
| nGrad(DD) | |||
| Interpolation | Linear | ||
| Toe Cap | Plate/Striker | ||
|---|---|---|---|
| Elastic modulus | 2.5 | 200 | GPa |
| Poisson ratio | 0.3 | 0.3 | - |
| Density | 1200 | 7850 | kg/m3 |
| Initial yield stress | 35.7 | - | MPa |
| Mesh Size and Additional Information | |||
|---|---|---|---|
| Component | Striker | M4 | Plates |
| Nr. of elements | 8168 | 670,640 | 8208 |
| Max. aspect ratio | 7.49 | 7.13 | 1.56 |
| Non orthogonality: | |||
| Maximum | 62.81 | 57.11 | 2.16 |
| Average | 18.42 | 3.15 | 0.56 |
| Max. skewness | 0.63 | 1.86 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, P.V.; Ramoa, B.; Machado, A.V.; Cardiff, P.; Nóbrega, J.M. Assessing the Compressive and Impact Behavior of Plastic Safety Toe Caps through Computational Modelling. Polymers 2021, 13, 4332. https://doi.org/10.3390/polym13244332
Rodrigues PV, Ramoa B, Machado AV, Cardiff P, Nóbrega JM. Assessing the Compressive and Impact Behavior of Plastic Safety Toe Caps through Computational Modelling. Polymers. 2021; 13(24):4332. https://doi.org/10.3390/polym13244332
Chicago/Turabian StyleRodrigues, Pedro Veiga, Bruno Ramoa, Ana Vera Machado, Philip Cardiff, and João Miguel Nóbrega. 2021. "Assessing the Compressive and Impact Behavior of Plastic Safety Toe Caps through Computational Modelling" Polymers 13, no. 24: 4332. https://doi.org/10.3390/polym13244332
APA StyleRodrigues, P. V., Ramoa, B., Machado, A. V., Cardiff, P., & Nóbrega, J. M. (2021). Assessing the Compressive and Impact Behavior of Plastic Safety Toe Caps through Computational Modelling. Polymers, 13(24), 4332. https://doi.org/10.3390/polym13244332