A Fuzzy Logic-Based Cost Modelling System for Recycling Carbon Fibre Reinforced Composites
Abstract
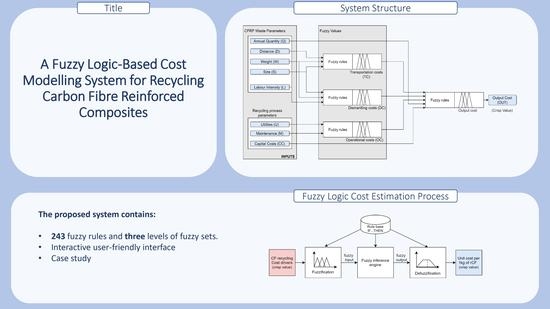
:1. Introduction
2. CFRP Recycling Cost Structure
2.1. Transportation Cost
2.2. Dismantling Cost
2.3. Operational Cost
2.4. Capital Cost
2.5. Fuzzy Ranges
3. Development of the Fuzzy Logic Cost Modelling System
3.1. Fuzzification
3.2. Fuzzy Inference
3.3. Defuzzification
4. System Application and Results of Fuzzy System
- As the weight of five main inputs (Q, CC, TC, OC, and DC (see Figure 1 for notation)) for the output cost is equal (based on developed rules), the change of two or more of these inputs has a significant impact. For example, it is evident that the higher capital cost in combination with the higher operational cost (Maintenance + Utility) lead to the resultant highest cost.
- Single inputs (CC, Q) without the first-level inputs have the highest effect on the output cost. This is clear from cases 7 and 8, where the increased annual quantity with similar other inputs decreased the output cost to almost 10%.
- Other input parameters for dismantling and transportation cost acting together become a cost-increasing factor. For instance, comparing cases 2 and 3, even though capital cost were lower for case 2 than for case 3, the increased input parameters for waste characteristics (labour intensity and size) yielded results of more expensive output cost. Labour-intensive large waste components require additional cost for dismantling and transportation.
- The accuracy of the system’s results is dependent on the chosen ranges for output cost and input parameters. The availability of data and expert knowledge is a critical factor for the correct implementation of the model. Ranges for output cost should be adjusted for the chosen market and country.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, W.; Huang, H.; Cheng, H.; Liu, Z. CFRP reclamation and remanufacturing based on a closed-loop recycling process for carbon fibers using supercritical N-butanol. Fibers Polym. 2020, 21, 604–618. [Google Scholar] [CrossRef]
- Deng, J.; Xu, L.; Zhang, L.; Peng, J.; Guo, S.; Liu, J.; Koppala, S. Recycling of carbon fibers from CFRP waste by microwave thermolysis. Processes 2019, 7, 207. [Google Scholar] [CrossRef] [Green Version]
- Akbar, A.; Liew, K. Assessing recycling potential of carbon fiber reinforced plastic waste in production of eco-efficient cement-based materials. J. Clean. Prod. 2020, 274, 123001. [Google Scholar] [CrossRef]
- Sukanto, H.; Raharjo, W.W.; Ariawan, D.; Triyono, J. Carbon fibers recovery from CFRP recycling process and their usage: A review. IOP Conf. Series: Mater. Sci. Eng. 2021, 1034, 012087. [Google Scholar] [CrossRef]
- Zhang, J.; Chevali, V.S.; Wang, H.; Wang, C.-H. Current status of carbon fibre and carbon fibre composites recycling. Compos. Part B: Eng. 2020, 193, 108053. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Seidlitz, H.; Krenz, J.; Goracy, K.; Urbaniak, M.; Rösch, J.J. Recycling of carbon fiber reinforced composite polymers—Review—Part 2: Recovery and application of recycled carbon fibers. Polymers 2020, 12, 3003. [Google Scholar] [CrossRef]
- Dong, P.A.V.; Azzaro-Pantel, C.; Cadene, A.-L. Economic and environmental assessment of recovery and disposal pathways for CFRP waste management. Resour. Conserv. Recycl. 2018, 133, 63–75. [Google Scholar] [CrossRef] [Green Version]
- Giorgini, L.; Benelli, T.; Brancolini, G.; Mazzocchetti, L. Recycling of carbon fiber reinforced composite waste to close their life cycle in a cradle-to-cradle approach. Curr. Opin. Green Sustain. Chem. 2020, 26, 100368. [Google Scholar] [CrossRef]
- Gopalraj, S.K.; Kärki, T. A review on the recycling of waste carbon fibre/glass fibre-reinforced composites: Fibre recovery, properties and life-cycle analysis. SN Appl. Sci. 2020, 2, 433. [Google Scholar] [CrossRef] [Green Version]
- Krauklis, A.E.; Karl, C.W.; Gagani, A.I.; Jørgensen, J.K. Composite material recycling technology—State-of-the-art and sustainable development for the 2020s. J. Compos. Sci. 2021, 5, 28. [Google Scholar] [CrossRef]
- Moens, E.; De Smit, K.; Marien, Y.; Trigilio, A.; Van Steenberge, P.; Van Geem, K.; Dubois, J.-L.; D’Hooge, D. Progress in reaction mechanisms and reactor technologies for thermochemical recycling of poly(methyl methacrylate). Polymers 2020, 12, 1667. [Google Scholar] [CrossRef]
- Fortman, D.J.; Brutman, J.P.; De Hoe, G.X.; Snyder, R.L.; Dichtel, W.R.; Hillmyer, M.A. Approaches to sustainable and continually recyclable cross-linked polymers. ACS Sustain. Chem. Eng. 2018, 6, 11145–11159. [Google Scholar] [CrossRef] [Green Version]
- Chapman, C.; Ward, S. Project Risk Management: Processes, Techniques and Insights; John Wiley & Sons: Chichester, UK, 2003. [Google Scholar]
- Shehab, E.; Alanazi, G.; Sarfraz, S. Towards recycling cost modelling framework for carbon fibre composites. In Proceedings of the 26th International Conference on Transdisciplinary Engineering, Tokyo, Japan, 30 July–1 August 2019; pp. 593–602. [Google Scholar] [CrossRef]
- Shehab, E.; Alanazi, G.; Sarfraz, S. Challenges in cost modelling of recycling carbon fiber composites. In Proceedings of the 27th International Conference on Transdisciplinary Engineering (TE2020), Warsaw, Poland, 1–10 July 2020; pp. 594–601. [Google Scholar] [CrossRef]
- Meiirbekov, A.; Shehab, E.; Amantayeva, A.; Suleimen, A.; Tokbolat, S.; Sarfraz, S. Understanding uncertainty in recycling Carbon fiber reinforced composites. In Proceedings of the 18th International Conference on Manufacturing Research (ICMR 2021), Derby, UK, 7–10 September 2021; pp. 166–171. [Google Scholar] [CrossRef]
- Özkan, I.; Türkşen, I.B. Uncertainty and fuzzy decisions. In Chaos Theory in Politics; Springer: Dordrecht, The Netherlands, 2014; pp. 17–27. [Google Scholar] [CrossRef]
- Shehab, E.; Abdalla, H. An intelligent knowledge-based system for product cost modelling. Int. J. Adv. Manuf. Technol. 2002, 19, 49–65. [Google Scholar] [CrossRef]
- Mason, A.K.; Kahn, D.J. Estimating costs with fuzzy logic. AACE Int. Trans. 1997, 3, 122–127. [Google Scholar]
- Wiehn, G.; Górak, A.; Pedrycz, W. Cost modelling of waste in incineration plants: An application of fuzzy sets toward decision making under uncertainty. Ecol. Model. 1996, 85, 83–91. [Google Scholar] [CrossRef]
- Chansaad, A.P.; Chaiprapat, S.; Yenradee, P. A parametric-fuzzy logic system for paint cost estimation of products with uncertain geometric characteristics. In Proceedings of the International Conference on Fuzzy Theory and Its Application, Taipei, Taiwan, 6–8 December 2013; pp. 482–487. Available online: https://ieeexplore.ieee.org/document/6825488 (accessed on 15 June 2021). [CrossRef]
- Phillis, Y.A.; Kouikoglou, V.S.; Zhu, X. Fuzzy assessment of material recyclability and its applications. J. Intell. Robot. Syst. 2008, 55, 21–38. [Google Scholar] [CrossRef]
- Keivanpour, S.; Kadi, D.A.; Mascle, C. Economic sustainability of end-of- life vehicle recycling infrastructure under uncertainty. A fuzzy logic approach. In Proceedings of the 5th IESM Conference, Rabat, Morocco, 28–30 October 2013; pp. 5–10. [Google Scholar]
- Li, X.; Bai, R.; McKechnie, J. Environmental and financial performance of mechanical recycling of carbon fibre reinforced polymers and comparison with conventional disposal routes. J. Clean. Prod. 2016, 127, 451–460. [Google Scholar] [CrossRef]
- Meng, F.; McKechnie, J.; Pickering, S.J. An assessment of financial viability of recycled carbon fibre in automotive applications. Compos. Part A: Appl. Sci. Manuf. 2018, 109, 207–220. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Cui, Y.; Pickering, S.; McKechnie, J. From aviation to aviation: Environmental and financial viability of closed-loop recycling of carbon fibre composite. Compos. Part B: Eng. 2020, 200, 108362. [Google Scholar] [CrossRef]
- Swedberg, S.; Svalstedt, M. Commercial Aircraft Wing Structure: Design of a Carbon Fiber Composite Structure. 2020. Available online: https://www.diva-portal.org/smash/get/diva2:1441558/FULLTEXT01.pdf (accessed on 20 June 2021).
- Ahmad, H.; Markina, A.A.; Porotnikov, M.V.; Ahmad, F. A review of carbon fiber materials in automotive industry. IOP Conf. Series: Mater. Sci. Eng. 2020, 971, 032011. [Google Scholar] [CrossRef]
- Irena.org. Wind Energy. 2020. Available online: https://www.irena.org/wind (accessed on 21 June 2021).
- Duval, G. How Big Are the Blades of a Wind Turbine? 2021. Available online: https://www.semprius.com/wind-turbine-blades-size/ (accessed on 21 June 2021).
- Nagle, A.J.; Delaney, E.L.; Bank, L.C.; Leahy, P.G. A comparative life cycle assessment between landfilling and co-processing of waste from decommissioned Irish wind turbine blades. J. Clean. Prod. 2020, 277, 123321. [Google Scholar] [CrossRef]
- Yuan, F.-C. The use of a fuzzy logic-based system in cost-volume-profit analysis under uncertainty. Expert Syst. Appl. 2009, 36, 1155–1163. [Google Scholar] [CrossRef]
- Pickering, S. Recycling technologies for thermoset composite materials—Current status. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1206–1215. [Google Scholar] [CrossRef]
- Cacciottolo, M. BBC News—How do you recycle a jumbo jet? 2010. Available online: http://news.bbc.co.uk/2/hi/uk_news/magazine/8542482.stm (accessed on 30 June 2021).
- Suncor Energy Products. Suncor Energy Adelaide Wind Power Project Decommissioning Plan Report. 2012. Available online: https://www.suncor.com/-/media/project/suncor/files/about-us/adelaide-wind-power-project/2012-11-adelaide-wind-power-project-decommissioning-plan-report-en.pdf?la=en-ca&modified=20210121181324&hash=76F5FD80B6B0BD64D3ED0920C60F61B5C980AE56 (accessed on 1 July 2021).
- Murphy. Operating Cost. 2021. Available online: https://www.investopedia.com/terms/o/operating-cost.asp (accessed on 1 July 2021).
- Howarth, J.; Mareddy, S.S.; Mativenga, P. Energy intensity and environmental analysis of mechanical recycling of carbon fibre composite. J. Clean. Prod. 2014, 81, 46–50. [Google Scholar] [CrossRef]
- Song, Y.S.; Youn, J.R.; Gutowski, T.G. Life cycle energy analysis of fiber-reinforced composites. Compos. Part A: Appl. Sci. Manuf. 2009, 40, 1257–1265. [Google Scholar] [CrossRef]
- Witik, R.A.; Teuscher, R.; Michaud, V.; Ludwig, C.; Månson, J.-A.E. Carbon fibre reinforced composite waste: An environmental assessment of recycling, energy recovery and landfilling. Compos. Part A: Appl. Sci. Manuf. 2013, 49, 89–99. [Google Scholar] [CrossRef]
- Meng, F.; McKechnie, J.; Turner, T.; Pickering, S. Energy and environmental assessment and reuse of fluidised bed recycled carbon fibres. Compos. Part A: Appl. Sci. Manuf. 2017, 100, 206–214. [Google Scholar] [CrossRef]
- Shibata, K.; Nakagawa, M. CFRP Recycling Technology Using Depolymerization under Ordinary Pressure. 2014. Available online: https://www.mc.showadenko.com/english/report/056/56_sou01.pdf (accessed on 10 July 2021).
- Keith, M.J.; Leeke, G.A. Optimisation of Solvolysis for Recycling Carbon Fibre Reinforced Composites. In Proceedings of the ECCM17—17th European Conference on Composite Materials, Munich, Germany, 26–30 June 2016; pp. 1–7. [Google Scholar]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L. Data normalisation techniques in decision making: Case study with TOPSIS method. Int. J. Inf. Decis. Sci. 2018, 10, 19. [Google Scholar] [CrossRef]
- Halliwell, S. End of Life Options for Composite Waste. 2006. Available online: https://compositesuk.co.uk/system/files/documents/endoflifeoptions.pdf (accessed on 12 July 2021).
- Knight, C. Recycling High-Performance Carbon Fiber Reinforced Polymer Composites Using Sub-Critical and Supercritical Water; Florida State University: Tallahassee, FL, USA, 2013; Available online: https://fsu.digital.flvc.org/islandora/object/fsu%3A183778/datastream/PDF/view (accessed on 15 July 2021).
- Mittal, A.; Parkash, K.; Mittal, H. Software cost estimation using fuzzy logic. ACM SIGSOFT Softw. Eng. Notes 2010, 35, 1–7. [Google Scholar] [CrossRef]
- Mamdani, E.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Kayacan, E.; Khanesar, M.A. Fundamentals of type-1 fuzzy logic theory. In Fuzzy Neural Networks for Real Time Control Applications; Kayacan, E., Khanesar, M.A., Eds.; Butterworth-Heinemann: Oxford, UK, 2016; pp. 13–24. [Google Scholar] [CrossRef]
- Wang, K. Computational intelligence in agile manufacturing engineering. In Agile Manufacturing: The 21st Century Competitive Strategy; Elsevier: Amsterdam, The Netherlands, 2001; pp. 297–315. [Google Scholar] [CrossRef]
- MATLAB. Defuzzification Methods. 2021. Available online: https://www.mathworks.com/help/fuzzy/defuzzification-methods.html (accessed on 15 August 2021).
- Rentizelas, A.; Trivyza, N.L.; Lichtenegger, G. Reverse logistics optimisation model for end-of-life wind turbine blades waste composites. In Proceedings of the International Joint Conference on Industrial Engineering and Operations Management—IJCIEOM 2019, Novi Sad, Serbia, 15–17 July 2019. [Google Scholar]
- Gignac, J. Wind Turbine Blades Don’t Have to End Up in Landfills. 2020. Available online: https://blog.ucsusa.org/james-gignac/wind-turbine-blades-recycling/ (accessed on 22 August 2021).













| Input Variable | Level | Range |
|---|---|---|
| Low | 0–200 | |
| Transportation distance (km) | Medium | 150–400 |
| High | 350–2000 | |
| Low | 1000–12,600 | |
| Weight (Wind Turbine blades) (kg) | Medium | 12,000–16,000 |
| High | 15,400–30,000 | |
| Low | 0.1–10 | |
| Volume (m3) | Medium | 8–50 |
| High | 45–200 | |
| Low | 4–40 | |
| Labour intensity (manhours) | Medium | 38–70 |
| High | 68–160 |
| Industry | Cost (EUR/kg) | References |
|---|---|---|
| Aerospace | 0.54 | [34] |
| Automotive | 1.53 | [24] |
| Wind turbine | 0.42 | [35] |
| Recycling Technique | Energy Consumption (MJ/kg) | References |
|---|---|---|
| Mechanical recycling | 0.27 (150 kg/h) 2.03 (10 kg/h) | [37] |
| Pyrolysis | 2.8 30 | [38] [39] |
| Fluidized bed process | 6 (at 12 kg/h·m2 feed rate) | [40] |
| Solvolysis | 63–91 | [41,42] |
| Technique | Capital Investment According to the Literature | Adjusted Capital Cost Up-to-Date | Capital Cost at a Capacity of 1000 Tons/Year | Normalized Values |
|---|---|---|---|---|
| Pyrolysis | 10,000,000 EUR for a capacity of avg. 50,000 tons per year [7] | 10,188,034 EUR for a capacity of avg. 50,000 tons per year | 974,335 EUR | 0.16 |
| Mechanical | 200,000 EUR for a capacity of 4000 tons per year [44] (only shredder) | 425,714 EUR for a capacity of 4000 tons per year (a hammer miller included) | 185,303 EUR | 0.03 |
| Fluidized bed | 4,100,000 EUR for a capacity of 1000 tons per year [25] | 4,379,211 EUR for a capacity of 1000 tons per year | 4,379,211 EUR | 0.72 |
| Supercritical Water | 5,770,000 EUR for a capacity of 150 kg per hour [45] | 6,065,115 EUR for a capacity of 150 kg per hour | 6,065,115 EUR | 1 |
| Output (Level 2) | Level | MECHANICAL | PYROLYSIS | FBP | SCW | ||||
|---|---|---|---|---|---|---|---|---|---|
| Cost | LOW | 1 | 1.3 | 1.6 | 2.1 | 1.7 | 2.2 | 14 | 16.8 |
| MEDIUM | 1.2 | 1.8 | 1.8 | 2.8 | 2 | 2.9 | 15.9 | 21.5 | |
| HIGH | 1.6 | 2.2 | 2.5 | 3.5 | 2.7 | 3.7 | 20.6 | 23.4 | |
| VERY HIGH | 2.1 | 3.5 | 3.2 | 5.5 | 3.4 | 5.9 | 22.5 | 28.1 | |
| Rule Rk | If ANNUAL QUANTITY Is | If TRANSPORTATION COST Is | If CAPITAL COST Is | If DISMANTLING COST Is | If OPERATIONAL COST Is | Then OUTPUT COST Is |
|---|---|---|---|---|---|---|
| R1 | low | low | low | low | low | low |
| R2 | low | low | low | low | medium | low |
| R3 | low | low | low | low | high | medium |
| R4 | low | low | low | medium | low | low |
| R5 | low | low | low | medium | medium | medium |
| … | ||||||
| R239 | high | high | high | medium | medium | medium |
| R240 | high | high | high | medium | high | high |
| R241 | high | high | high | high | low | medium |
| R242 | high | high | high | high | medium | high |
| R243 | high | high | high | high | high | high |
| CASE No. | INPUTS | OUTPUT Cost (EUR/kg) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Recycling Technique Parameters | Waste Characteristics | |||||||||||
| Capital Cost | Maintenance | Utility Level | Weight, kg | Size, m3 | Labour Intensity, Manhours | Distance, km | Annual Quantity, tons | Mechanical | Pyrolysis | FB | SCW | |
| 1 | MEDIUM | LOW | LOW | 100 | 10 | 5 | 250 | 1500 | 1.15 | 1.7807 | 1.88 | 18.6992 |
| 2 | MEDIUM | LOW | LOW | 50 | 1 | 10 | 200 | 1500 | 1.3 | 1.7751 | 1.8748 | 15.0128 |
| 3 | LOW | MEDIUM | LOW | 2500 | 50 | 80 | 500 | 2900 | 1.5 | 2.3227 | 2.4501 | 18.6998 |
| 4 | MEDIUM | MEDIUM | LOW | 1200 | 2 | 40 | 1000 | 1500 | 1.5 | 2.3281 | 2.4502 | 18.6996 |
| 5 | HIGH | MEDIUM | LOW | 500 | 50 | 70 | 100 | 500 | 1.9 | 2.5768 | 3.2 | 21.9997 |
| 6 | HIGH | HIGH | MEDIUM | 1500 | 5 | 30 | 1500 | 1250 | 1.5 | 2.3248 | 3.55 | 22 |
| 7 | HIGH | HIGH | HIGH | 4000 | 8 | 70 | 1000 | 500 | 2.8 | 4.5398 | 4.8242 | 24.6484 |
| 8 | HIGH | HIGH | HIGH | 4000 | 15 | 80 | 1000 | 2250 | 2.53 | 4.0954 | 4.2743 | 24.3502 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shehab, E.; Meiirbekov, A.; Amantayeva, A.; Suleimen, A.; Tokbolat, S.; Sarfraz, S.; Ali, M.H. A Fuzzy Logic-Based Cost Modelling System for Recycling Carbon Fibre Reinforced Composites. Polymers 2021, 13, 4370. https://doi.org/10.3390/polym13244370
Shehab E, Meiirbekov A, Amantayeva A, Suleimen A, Tokbolat S, Sarfraz S, Ali MH. A Fuzzy Logic-Based Cost Modelling System for Recycling Carbon Fibre Reinforced Composites. Polymers. 2021; 13(24):4370. https://doi.org/10.3390/polym13244370
Chicago/Turabian StyleShehab, Essam, Arshyn Meiirbekov, Akniyet Amantayeva, Aidar Suleimen, Serik Tokbolat, Shoaib Sarfraz, and Md Hazrat Ali. 2021. "A Fuzzy Logic-Based Cost Modelling System for Recycling Carbon Fibre Reinforced Composites" Polymers 13, no. 24: 4370. https://doi.org/10.3390/polym13244370
APA StyleShehab, E., Meiirbekov, A., Amantayeva, A., Suleimen, A., Tokbolat, S., Sarfraz, S., & Ali, M. H. (2021). A Fuzzy Logic-Based Cost Modelling System for Recycling Carbon Fibre Reinforced Composites. Polymers, 13(24), 4370. https://doi.org/10.3390/polym13244370