Mathematical Modeling of Outdoor Natural Weathering of Polycarbonate: Regional Characteristics of Degradation Behaviors
Abstract
:1. Introduction
2. Experimental
2.1. Samples
2.2. Exposure Tests
2.3. Color Measurement
3. Theory
3.1. Modeling of Degradation Rate Function
3.2. Contribution Ratio of Degradational Factors
3.3. Cross-Correlation Analysis
4. Results and Discussion
4.1. Environmental Data and Surface Temperature Estimation
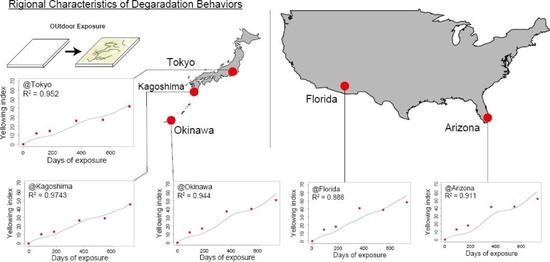
4.2. Outdoor Aging Behavior of Appearance Quality
4.3. Reproducing Outdoor Aging Behavior from the Environmental Dataset
4.4. Contribution of Climate Conditions
4.5. Effects of Phase Between Climate Factors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diepens, M.; Gijsman, P. Photodegradation of bisphenol A polycarbonate. Polym. Degrad. Stab. 2007, 92, 397–406. [Google Scholar] [CrossRef]
- Pickett, J.E. Influence of photo-Fries reaction products on the photodegradation of bisphenol-A polycarbonate. Polym. Degrad. Stab. 2011, 96, 2253–2265. [Google Scholar] [CrossRef]
- Pickett, J.E.; Gardner, M.M. Reproducibility of Florida weathering data. Polym. Degrad. Stab. 2005, 90, 418–430. [Google Scholar] [CrossRef]
- Coyle, D.J. Life prediction for CIGS solar modules part 1: Modeling moisture ingress and degradation. Prog. Photovolt. Res. Appl. 2013, 21, 156–172. [Google Scholar] [CrossRef]
- Peck, D.S. Comprehensive Model for Humidity Testing Correlation. In Proceedings of the 24th International Reliability Physics Symposium, Anaheim, CA, USA, 1–3 April 1986; pp. 44–50. [Google Scholar]
- Hertz, D.; Azaria, M. Time delay estimation between two phase shifted signals via generalized cross-correlation methods. Signal Process. 1985, 8, 235–257. [Google Scholar] [CrossRef]
- Tocháček, J.; Vrátníčková, Z. Polymer life-time prediction: The role of temperature in UV accelerated ageing of polypropylene and its copolymers. Polym. Test. 2014, 36, 82–87. [Google Scholar] [CrossRef]
- Bauer, D.R. Global exposure models for automotive coating photo-oxidation. Polym. Degrad. Stab. 2000, 69, 297–306. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, M.; Zhou, Y.; Wang, S.; Li, G.; Jiang, L.; Dan, Y. Aging life prediction system of polymer outdoors constructed by ANN. 1. Lifetime prediction for polycarbonate. Polym. Degrad. Stab. 2014, 105, 218–236. [Google Scholar] [CrossRef]
- Carlsson, B.; Möller, K.; Köhl, M.; Heck, M.; Brunold, S.; Frei, U.; Marechal, J.-C.; Jorgensen, G. The applicability of accelerated life testing for assessment of service life of solar thermal components. Sol. Energy Mater. Sol. Cells 2004, 84, 255–274. [Google Scholar] [CrossRef]
- Celina, M.C. Review of polymer oxidation and its relationship with materials performance and lifetime prediction. Polym. Degrad. Stab. 2013, 98, 2419–2429. [Google Scholar] [CrossRef]
- Striny, K.; Schelling, A. Reliability Evaluation of Aluminum-Metallized MOS Dynamic RAM’s in Plastic Packages in High Humidity and Temperature Environments. IEEE Trans. Compon. Hybrids Manuf. Technol. 1981, 4, 476–481. [Google Scholar] [CrossRef]
- Martin, J.W.; Chin, J.W.; Nguyen, T. Reciprocity law experiments in polymeric photodegradation: A critical review. Prog. Org. Coat. 2003, 47, 292–311. [Google Scholar] [CrossRef]
- Sierra-Porta, D. Cross correlation and time-lag between cosmic ray intensity and solar activity during solar cycles 21, 22 and 23. Astrophys. Space Sci. 2018, 363, 137. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, G.; Bingham, C.; Netter, J.; Goggin, R. Service Life Prediction of Organic Coatings: A Systems Approach Chapter 11. A Unique Facility for Ultra-Accelerated Natural Sunlight Exposure Testing of Materials; Bauer, D.R., Martin, J., Eds.; Oxford University Press: Oxford, UK, 1999; pp. 170–185. [Google Scholar]
- Pickett, J.E.; Sargent, J.R. Sample temperatures during outdoor and laboratory weathering exposures. Polym. Degrad. Stab. 2009, 94, 189–195. [Google Scholar] [CrossRef]
- Andrady, A.L.; Searle, N.D.; Crewdson, L.F.E. Wavelength sensitivity of unstabilized and UV stabilized polycarbonate to solar simulated radiation. Polym. Degrad. Stab. 1992, 35, 235–247. [Google Scholar] [CrossRef]
- Factor, A.; Ligon, W.V.; May, R.J. The role of oxygen in the photoaging of bisphenol A polycarbonate. 2. GC/GC/high-resolution MS analysis of Florida-weathered polycarbonate. Macromolecules 1987, 20, 2461–2468. [Google Scholar] [CrossRef]
- Tjandraatmadja, G.F.; Burn, L.S.; Jollands, M.C. Evaluation of commercial polycarbonate optical properties after QUV-A radiation—the role of humidity in photodegradation. Polym. Degrad. Stab. 2002, 78, 435–448. [Google Scholar] [CrossRef]
- Avenel, C.; Raccurt, O.; Gardette, J.-L.; Therias, S. Review of accelerated ageing test modelling and its application to solar mirrors. Sol. Energy Mater. Sol. Cells 2018, 186, 29–41. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Nguyen Tri, P.; Nguyen, T.D.; El Aidani, R.; Trinh, V.T.; Decker, C. Accelerated degradation of water borne acrylic nanocomposites used in outdoor protective coatings. Polym. Degrad. Stab. 2016, 128, 65–76. [Google Scholar] [CrossRef]










| Location | Duration | (MJ/m2⋅year) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Tokyo | Aug. 2013 ~ July 2015 | 16.6 | 21.7 | 11.8 | 0.77 | 53.6 | 26.2 | 1876 | 45 |
| Kagoshima | 15.9 | 20.0 | 12.8 | 0.94 | 87.0 | 18.5 | 2791 | 30 | |
| Okinawa | 23.3 | 26.3 | 20.9 | 1.00 | 77.2 | 27.6 | 1577 | 20 | |
| Florida | Sep. 2013 ~ Aug. 2015 | 24.5 | 30.4 | 19.6 | 0.87 | 74.1 | 28.1 | 3876 | 26 |
| Arizona | 22.7 | 31.3 | 14.0 | 0.90 | 33.1 | 23.9 | 237.0 | 45 |
| Property | Sample | (%) | ||
|---|---|---|---|---|
| ⊿YI | PC1 | 0.99 | 18.06 | |
| PC4 | 0.32 | 10.70 | ||
| Gloss retention | PC1 | 0.16 | 10.94 | |
| PC4 | 10.71 | 0.05 |
| Non-stabilized,⊿YI | Stabilized,⊿YI | ||||
| Tokyo | 67.2 | 32.8 | Tokyo | 53.1 | 46.9 |
| Kagoshima | 70.2 | 29.8 | Kagoshima | 53.6 | 43.4 |
| Okinawa | 74.8 | 25.2 | Okinawa | 62.2 | 37.8 |
| Florida | 74.9 | 25.1 | Florida | 62.4 | 37.6 |
| Arizona | 64.3 | 35.7 | Arizona | 49.9 | 50.1 |
| Non-stabilized, Gloss loss | Stabilized, Gloss loss | ||||
| Tokyo | 67.2 | 32.8 | Tokyo | 53.1 | 46.9 |
| Kagoshima | 70.2 | 29.8 | Kagoshima | 53.6 | 43.4 |
| Okinawa | 74.8 | 25.2 | Okinawa | 62.2 | 37.8 |
| Florida | 74.9 | 25.1 | Florida | 62.4 | 37.6 |
| Arizona | 64.3 | 35.7 | Arizona | 49.9 | 50.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishida, T.; Kitagaki, R. Mathematical Modeling of Outdoor Natural Weathering of Polycarbonate: Regional Characteristics of Degradation Behaviors. Polymers 2021, 13, 820. https://doi.org/10.3390/polym13050820
Ishida T, Kitagaki R. Mathematical Modeling of Outdoor Natural Weathering of Polycarbonate: Regional Characteristics of Degradation Behaviors. Polymers. 2021; 13(5):820. https://doi.org/10.3390/polym13050820
Chicago/Turabian StyleIshida, Takato, and Ryoma Kitagaki. 2021. "Mathematical Modeling of Outdoor Natural Weathering of Polycarbonate: Regional Characteristics of Degradation Behaviors" Polymers 13, no. 5: 820. https://doi.org/10.3390/polym13050820
APA StyleIshida, T., & Kitagaki, R. (2021). Mathematical Modeling of Outdoor Natural Weathering of Polycarbonate: Regional Characteristics of Degradation Behaviors. Polymers, 13(5), 820. https://doi.org/10.3390/polym13050820