Changes in Electrical Conductance of Polymer Composites Melts Due to Carbon Nanofiller Particles Migration
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Composite Processing
2.2.2. Methods of Investigation
2.2.3. Modeling the Processes of Filler Migration to the Composite Surface
3. Results
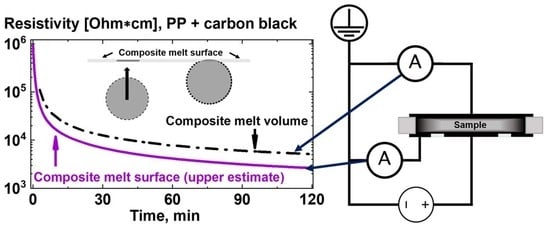
3.1. Experimental Studies
3.2. Numerical Studies
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bose, S.; Özdilek, C.; Leys, J.; Seo, J.W.; Wübbenhorst, M.; Vermant, J.; Moldenaers, P. Phase separation as a tool to control dispersion of multiwall carbon nanotubes in polymeric blends. ACS Appl. Mater. Interfaces 2010, 2, 800–807. [Google Scholar] [CrossRef]
- Tang, Y.; Lewin, M.; Pearce, E.M. Effects of annealing on the migration behavior of pa6/clay nanocomposites. Macromol. Rapid Commun. 2006, 27, 1545–1549. [Google Scholar] [CrossRef]
- Tao, F.; Nysten, B.; Baudouin, A.-C.; Thomassin, J.-M.; Vuluga, D.; Detrembleur, C.; Bailly, C. Influence of nanoparticle–polymer interactions on the apparent migration behaviour of carbon nanotubes in an immiscible polymer blend. Polymer 2011, 52, 4798–4805. [Google Scholar] [CrossRef]
- Xiong, Z.-Y.; Wang, L.; Sun, Y.; Guo, Z.-X.; Yu, J. Migration of MWCNTs during melt preparation of ABS/PC/MWCNT conductive composites via PC/MWCNT masterbatch approach. Polymer 2013, 54, 447–455. [Google Scholar] [CrossRef]
- Alig, I.; Lellinger, D.; Dudkin, S.M.; Pötschke, P. Conductivity spectroscopy on melt processed polypropylene–multiwalled carbon nanotube composites: Recovery after shear and crystallization. Polymer 2007, 48, 1020–1029. [Google Scholar] [CrossRef]
- Alig, I.; Skipa, T.; Engel, M.; Lellinger, D.; Pegel, S.; Pötschke, P. Electrical conductivity recovery in carbon nanotube–polymer composites after transient shear. Phys. Status Solidi 2007, 244, 4223–4226. [Google Scholar] [CrossRef]
- Deng, H.; Skipa, T.; Zhang, R.; Lellinger, D.; Bilotti, E.; Alig, I.; Peijs, T. Effect of melting and crystallization on the conductive network in conductive polymer composites. Polymer 2009, 50, 3747–3754. [Google Scholar] [CrossRef]
- Heinrich, G.; Costa, F.R.; Abdel-Goad, M.; Wagenknecht, U. Structural kinetics in filled elastomers and PE/LDH composites. Kautschuk Gummi Kunststoffe 2005, 58, 163–167. [Google Scholar]
- Fournier, J.; Boiteux, G.; Seytre, G.; Marichy, G. Percolation network of polypyrrole in conducting polymer composites. Synth. Met. 1997, 84, 839–840. [Google Scholar] [CrossRef]
- Pegel, S.; Pötschke, P.; Petzold, G.; Alig, I.; Dudkin, S.M.; Lellinger, D. Dispersion, agglomeration, and network formation of multiwalled carbon nanotubes in polycarbonate melts. Polymer 2008, 49, 974–984. [Google Scholar] [CrossRef]
- Salehiyan, R.; Ray, S.S. Tuning the conductivity of nanocomposites through nanoparticle migration and interface crossing in immiscible polymer blends: A review on fundamental understanding. Macromol. Mater. Eng. 2019, 304. [Google Scholar] [CrossRef]
- Teng, C.-Y.; Sheng, Y.-J.; Tsao, H.-K. Surface segregation and bulk aggregation in an athermal thin film of polymer–nanoparticle blends: Strategies of controlling phase behavior. Langmuir 2017, 33, 2639–2645. [Google Scholar] [CrossRef] [PubMed]
- Lekkerkerker, H.N.; Tuinier, R. Colloids and the Depletion Interaction; Metzler, J.B., Ed.; Springer: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Sukenik, S.; Sapir, L.; Harries, D. Balance of enthalpy and entropy in depletion forces. Curr. Opin. Colloid Interface Sci. 2013, 18, 495–501. [Google Scholar] [CrossRef] [Green Version]
- Edwards, T.D.; Bevan, M.A. Depletion-mediated potentials and phase behavior for micelles, macromolecules, nanoparticles, and hydrogel particles. Langmuir 2012, 28, 13816–13823. [Google Scholar] [CrossRef] [PubMed]
- Grekhov, A.M.; Eremin, Y.S. Influence of carbon-nanotube concentration in chloroform on the kinetics of agglomeration and sedimentation. Nanotechnol. Russia 2015, 10, 523–529. [Google Scholar] [CrossRef]
- Blythe, T.; Bloor, D. Electrical Properties of Polymers, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008; ISBN 978-0521558389. [Google Scholar]
- Sahimi, M. Applications of Percolation Theory, 1st ed.; Routledge: London, UK, 1994; ISBN 978-0748400768. [Google Scholar]
- Stauffer, D.; Aharony, A.; Redner, S. Introduction to percolation theory. Phys. Today 1993, 46, 64. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, B.-Y.; Wang, W.-J.; Guo, Z.-X.; Yu, J. Highly efficient electrically conductive networks in carbon-black-filled ternary blends through the formation of thermodynamically induced self-assembled hierarchical structures. J. Appl. Polym. Sci. 2018, 135, 45877. [Google Scholar] [CrossRef]
- Katada, A.; Konishi, Y.; Isogai, T.; Tominaga, Y.; Asai, S.; Sumita, M. Dynamic percolation phenomenon of poly (methyl methacrylate)/surface fluorinated carbon black composite. J. Appl. Polym. Sci. 2003, 89, 1151–1155. [Google Scholar] [CrossRef]
- Wu, G.; Asai, S.; Sumita, M. Carbon black as a self-diagnosing probe to trace polymer dynamics in highly filled compositions. Macromolecules 2002, 35, 1708–1713. [Google Scholar] [CrossRef]
- Wu, G.; Asai, S.; Zhang, C.; Miura, T.; Sumita, M. A delay of percolation time in carbon-black-filled conductive polymer composites. J. Appl. Phys. 2000, 88, 1480–1487. [Google Scholar] [CrossRef]
- Zhao, Y.; Byshkin, M.; Cong, Y.; Kawakatsu, T.; Guadagno, L.; De Nicola, A.; Yu, N.; Milano, G.; Dong, B. Self-assembly of carbon nanotubes in polymer melts: Simulation of structural and electrical behaviour by hybrid particle-field molecular dynamics. Nanoscale 2016, 8, 15538–15552. [Google Scholar] [CrossRef] [PubMed]
- Gumerov, R.A.; Rudov, A.A.; Richtering, W.; Möller, M.; Potemkin, I.I. Amphiphilic arborescent copolymers and microgels: From unimolecular micelles in a selective solvent to the stable monolayers of variable density and nanostructure at a liquid interface. ACS Appl. Mater. Interfaces 2017, 9, 31302–31316. [Google Scholar] [CrossRef]
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
- Lebedev, O.V.; Bogdanova, O.I.; Goncharuk, G.P.; Ozerin, A.N. Tribological and percolation properties of polypropylene/nanodiamond soot composites. Polym. Polym. Compos. 2019, 28, 369–377. [Google Scholar] [CrossRef]
- Abbasi, H.; Antunes, M.; Velasco, J.I. Recent advances in carbon-based polymer nanocomposites for electromagnetic interference shielding. Prog. Mater. Sci. 2019, 103, 319–373. [Google Scholar] [CrossRef]
- PP H030 GP/3. Available online: http://www.sibur-int.com/upload/documents/TDSH030GP3v14.pdf (accessed on 29 December 2020).
- P267-E. Available online: https://studylib.ru/doc/2305578/e-lektroprovodnyj-tehnicheskij-uglerod-p-267-e---p-268 (accessed on 29 December 2020).
- Graphene Supermarket. Available online: https://graphene_supermarket.com (accessed on 25 December 2020).
- Nanocyl. Available online: https://www.nanocyl.com/product/nc7000/ (accessed on 25 December 2020).
- Tuball. Available online: https://tuball.com/en/about-tuball (accessed on 25 December 2020).
- Krestinin, A.V.; Dremova, N.N.; Knerel’Man, E.I.; Blinova, L.N.; Zhigalina, V.G.; Kiselev, N.A. Characterization of SWCNT products manufactured in Russia and the prospects for their industrial application. Nanotechnol. Russ. 2015, 10, 537–548. [Google Scholar] [CrossRef]
- LAMMPS. Available online: http://lammps.sandia.gov (accessed on 31 January 2021).
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Frenkel, D.; Smit, B.; Ratner, M.A. Understanding molecular simulation: From algorithms to applications. Phys. Today 1997, 50, 66. [Google Scholar] [CrossRef]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302–1322. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Mechanics of Chain Molecules, 2nd ed.; Hanser Publishers: New York, NY, USA, 1989. [Google Scholar]
- Lee, H.S.; Yun, C.H.; Kim, H.M.; Lee, C.J. Persistence length of multiwalled carbon nanotubes with static bending. J. Phys. Chem. C 2007, 111, 18882–18887. [Google Scholar] [CrossRef]
- Everaers, R.; Ejtehadi, M.R. Interaction potentials for soft and hard ellipsoids. Phys. Rev. E 2003, 67, 041710. [Google Scholar] [CrossRef] [Green Version]
- And, K.A.F.; Qin, Y. Molecular-dynamics simulation of colloidal nanoparticle forces. Ind. Eng. Chem. Res. 2006, 45, 5477–5481. [Google Scholar] [CrossRef]
- Rahaman, M.; Aldalbahi, A.; Govindasami, P.; Khanam, N.P.; Bhandari, S.; Feng, P.; Altalhi, T. A new insight in determining the percolation threshold of electrical conductivity for extrinsically conducting polymer composites through different sigmoidal models. Polymers 2017, 9, 527. [Google Scholar] [CrossRef]
- Lisunova, M.; Mamunya, Y.; Lebovka, N.; Melezhyk, A. Percolation behaviour of ultrahigh molecular weight polyethylene/multi-walled carbon nanotubes composites. Eur. Polym. J. 2007, 43, 949–958. [Google Scholar] [CrossRef]
- Powell, M.J. Site percolation in randomly packed spheres. Phys. Rev. B 1979, 20, 4194–4198. [Google Scholar] [CrossRef]
- Capuani, F.; Pagonabarraga, I.; Frenkel, D. Lattice-Boltzmann simulation of the sedimentation of charged disks. J. Chem. Phys. 2006, 124, 124903. [Google Scholar] [CrossRef] [Green Version]
- Nair, N.; Kim, W.-J.; Braatz, A.R.D.; Strano, M.S. Dynamics of surfactant-suspended single-walled carbon nanotubes in a centrifugal field. Langmuir 2008, 24, 1790–1795. [Google Scholar] [CrossRef]
- Panalytical, M. Combining Dynamic Light Scattering and Raman Spectroscopy to Characterize Single Wall Carbon Nanotubes (SWNTs). Available online: https://www.azonano.com/article.aspx?ArticleID=4133 (accessed on 3 April 2020).
- Subramanian, M.N. Polymer Blends and Composites: Chemistry and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 153–168. [Google Scholar]
- Zhbanov, A.I.; Pogorelov, E.G.; Chang, Y.-C. Van der Waals interaction between two crossed carbon nanotubes. ACS Nano 2010, 4, 5937–5945. [Google Scholar] [CrossRef] [Green Version]
- Chiou, Y.-C.; Olukan, T.A.; AlMahri, M.A.; Apostoleris, H.; Chiu, C.H.; Lai, C.-Y.; Lu, J.-Y.; Santos, S.; Almansouri, I.; Chiesa, M. Direct measurement of the magnitude of the van der waals interaction of single and multilayer graphene. Langmuir 2018, 34, 12335–12343. [Google Scholar] [CrossRef] [PubMed]
- Lewin, M.; Frank, R.; Mey-Marom, A. Surface free energies of polymeric materials, additives and minerals. Polym. Adv. Technol. 2005, 16, 429–441. [Google Scholar] [CrossRef]
- Asai, S.; Sakata, K.; Sumita, M.; Miyasaka, K. Effect of interfacial free energy on the heterogeneous distribution of oxidized carbon black in polymer blends. Polym. J. 1992, 24, 415–420. [Google Scholar] [CrossRef]
- Chervanyov, A.I. Depletion forces acting on nanoparticles in confined polymer systems: Potential theory. Phys. Rev. E 2011, 83, 061801. [Google Scholar] [CrossRef] [PubMed]
- Miura, T.; Seki, K. Diffusion influenced adsorption kinetics. J. Phys. Chem. B 2015, 119, 10954–10961. [Google Scholar] [CrossRef] [PubMed]


















| Filler Type | Filler Content, wt.% | PP Content, cc, wt.% | Sample Code |
|---|---|---|---|
| CB | 12.5 | 87.5 | PP + 12.5 wt.% CB |
| 15 | 85 | PP + 15 wt.% CB | |
| GnPs | 10 | 90 | PP + 10 wt.% GnPs |
| MWCNTs | 1 | 99 | PP + 1 wt.% MWCNTs |
| 7.5 | 92.5 | PP + 7.5 wt.% MWCNTs | |
| SWCNTs | 0.5 | 99.5 | PP + 0.5 wt.% SWCNTs |
| 7.5 | 92.5 | PP + 7.5 wt.% SWCNTs |
| Filler | Experimental, cc, wt.% | Theoretical, cc, wt.% |
|---|---|---|
| CB | 14 ± 1 | 35 |
| GnPs | 22 ± 1 | 20 |
| MWCNTs | 3 ± 0.5 | 1.1 |
| SWCNTs | 1 ± 0.2 | 0.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lebedev, O.V.; Goncharuk, G.P.; Ozerin, A.N. Changes in Electrical Conductance of Polymer Composites Melts Due to Carbon Nanofiller Particles Migration. Polymers 2021, 13, 1030. https://doi.org/10.3390/polym13071030
Lebedev OV, Goncharuk GP, Ozerin AN. Changes in Electrical Conductance of Polymer Composites Melts Due to Carbon Nanofiller Particles Migration. Polymers. 2021; 13(7):1030. https://doi.org/10.3390/polym13071030
Chicago/Turabian StyleLebedev, Oleg V., Galina P. Goncharuk, and Alexander N. Ozerin. 2021. "Changes in Electrical Conductance of Polymer Composites Melts Due to Carbon Nanofiller Particles Migration" Polymers 13, no. 7: 1030. https://doi.org/10.3390/polym13071030
APA StyleLebedev, O. V., Goncharuk, G. P., & Ozerin, A. N. (2021). Changes in Electrical Conductance of Polymer Composites Melts Due to Carbon Nanofiller Particles Migration. Polymers, 13(7), 1030. https://doi.org/10.3390/polym13071030