Complexation in Aqueous Solution of a Hydrophobic Polyanion (PSSNa) Bearing Different Charge Densities with a Hydrophilic Polycation (PDADMAC)
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Solution Behavior and Conformation of P(St-co-SSNa)
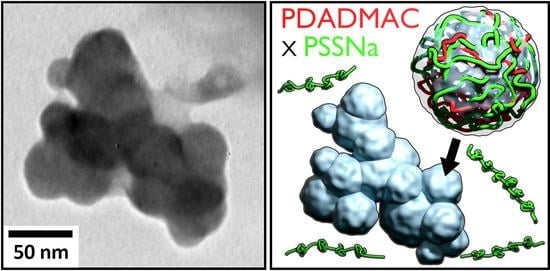
3.2. Observations of P(St-co-SSNa)-PDADMAC Complexes
3.3. Characterization of P(St-co-SSNa)-PDADMAC Complexes by DLS and Zetametry
3.4. Characterization of P(St-co-SSNa)-PDADMAC Complexation by ITC
3.5. Spectrophotometric Titration of P(St-co-SSNa) with Toluidine Blue
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meka, V.S.; Sing, M.K.G.; Pichika, M.R.; Nali, S.R.; Kolapalli, V.R.M.; Kesharwani, P. A comprehensive review on polyelectrolyte complexes. Drug Discov. Today 2017, 22, 1697–1706. [Google Scholar] [CrossRef] [PubMed]
- Thunemann, A.F.; Müller, M.; Dautzenberg, H.; Joanny, J.F.O.; Lowne, H. Polyelectrolyte Complexes. Adv. Polym. Sci. 2004, 166, 113–171. [Google Scholar]
- Kabanov, V. Fundamentals of Polyelectrolyte Complexes in Solution and the Bulk. In Multilayer Thin Films; Decher, G., Schlenoff, J.B., Eds.; WILEI-VCH: Weinheim, Germany, 2003; pp. 47–86. [Google Scholar]
- Tsuchida, E.; Abe, K. Interactions between macromolecules in solution and intermacromolecular complexes. Adv. Polym. Sci. 1982, 45, 1–119. [Google Scholar]
- Philipp, B.; Dautzenberg, H.; Linow, K.J.; Koetz, J.; Dawydoff, W. Polyelectrolyte complexes—recent developments and open problems. Prog. Polym. Sci. 1989, 14, 91–172. [Google Scholar] [CrossRef]
- Nasser, M.S.; Twaiq, F.A.; Onaizi, S.A. Effect of Polyelectrolytes on the Degree of Flocculation of Papermaking Suspensions. Sep. Purif. Technol. 2013, 103, 43–52. [Google Scholar] [CrossRef]
- Schmitt, C.; Turgeon, S.L. Protein/polysaccharide Complexes and Coacervates in Food Systems. Adv. Colloid Interface Sci. 2011, 167, 63–70. [Google Scholar] [CrossRef]
- Crini, G. Recent Developments in Polysaccharide-Based Materials Used as Adsorbents in Wastewater Treatment. Prog. Polym. Sci. 2005, 30, 38–70. [Google Scholar] [CrossRef]
- Kulkarni, A.D.; Vanjari, Y.H.; Sancheti, K.H.; Patel, H.M.; Belgamwar, V.S.; Surana, S.J.; Pardeshi, C.V. Polyelectrolyte complexes: Mechanisms, critical experimental aspects, and applications. Artif. Cells Nanomed. Biotechnol. 2016, 44, 1615–1625. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Fauquignon, M.; Haddou, M.; Schatz, C.; Chapel, J.-P. Interfacial Behavior of Solid- and Liquid-like Polyelectrolyte Complexes as a Function of Charge Stoichiometry. Polymers 2021, 13, 3848. [Google Scholar] [CrossRef]
- Wang, Q.; Schlenoff, J.B. The Polyelectrolyte Complex/Coacervate Continuum. Macromolecules 2014, 47, 3108–3116. [Google Scholar] [CrossRef]
- Dautzenberg, H. Polyelectrolyte complex formation in highly aggregating systems. 1. Effect of salt: Polyelectrolyte complex formation in the presence of NaCl. Macromolecules 1997, 30, 7810–7815. [Google Scholar] [CrossRef]
- Kabanov, V.A.; Zezin, A.B. A new class of complex water-soluble polyelectrolytes. Makromol. Chem. 1984, 6, 259–276. [Google Scholar] [CrossRef]
- Dautzenberg, H.; Hartmann, J.; Grunewald, S.; Brand, F. Stoichiometry and structure of polyelectrolyte complex particles in diluted solutions. Ber. Bunsenges. Phys. Chem. 1996, 100, 1024–1032. [Google Scholar] [CrossRef]
- Lebovka, N.I. Aggregation of Charged Colloidal Particles. In Polyelectrolyte Complexes in the Dispersed and Solid State I: Principles and Theory; Müller, M., Ed.; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 255, pp. 57–96. [Google Scholar]
- Starchenko, V.; Müller, M.; Lebovka, N.I. Sizing of PDADMAC/PSS Complex Aggregates by Polyelectrolyte and Salt Concentration and PSS Molecular Weight. J. Phys. Chem. 2012, 116, 14961–14967. [Google Scholar] [CrossRef] [PubMed]
- Brand, F.; Dautzenberg, H. Structural Analysis in Interpolyelectrolyte Complex Formation of Sodium Poly (styrenesulfonate) and Diallyldimethylammonium Chloride–Acrylamide Copolymers by Viscometry. Langmuir 1997, 13, 2905–2910. [Google Scholar] [CrossRef]
- Mende, M.; Schwarz, S.; Zschoche, S.; Petzold, G.; Janke, A. Influence of the Hydrophobicity of Polyelectrolytes on Polyelectrolyte Complex Formation and Complex Particle Structure and Shape. Polymers 2011, 3, 1363–1376. [Google Scholar] [CrossRef] [Green Version]
- Gummel, J.; Cousin, F.; Boué, B. Structure Transition in PSS/Lysozyme Complexes: A Chain-Conformation-Driven Process, as Directly Seen by Small Angle Neutron Scattering. Macromolecules 2008, 41, 2898–2907. [Google Scholar] [CrossRef] [Green Version]
- Gummel, J.; Boué, B.; Clemens, D.; Cousin, F. Finite size and inner structure controlled by electrostatic screening in globular complexes of proteins and polyelectrolyte. Soft Matter 2008, 4, 1653–1664. [Google Scholar] [CrossRef] [Green Version]
- Dautzenberg, H.; Görnitz, E.; Jaeger, W. Synthesis and characterization of poly (diallyldimethylammonium chloride) in a broad range of molecular weight. Macromol. Chem. Phys. 1998, 199, 1561–1571. [Google Scholar] [CrossRef]
- Ben Mahmoud, S.; Essafi, W.; Brûlet, A.; Boué, F. How necklace pearls evolve in hydrophobic polyelectrolyte chains under good solvent addition: A SANS study of the conformation. Macromolecules 2018, 51, 9259–9275. [Google Scholar] [CrossRef]
- Dautzenberg, H.; Rother, G.J. Interpretation of light scattering from supermolecular structures in liquid systems by master curves. J. Polym. Sci. Polym. Phys. 1988, 26, 353–366. [Google Scholar] [CrossRef]
- Dautzenberg, H.; Rother, G. Supermolecular structures in polymer solutions interpretation of static light scattering data. Makromol. Chem. Macromol. Symp. 1992, 61, 94–113. [Google Scholar] [CrossRef] [Green Version]
- Dobrynin, A.V.; Rubinstein, M.; Obukhov, S.P. Cascade of Transitions of Polyelectrolytes in Poor Solvents. Macromolecules 1996, 29, 2974–2979. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M. Hydrophobic polyelectrolytes. Macromolecules 1999, 32, 915–922. [Google Scholar] [CrossRef]
- Baigl, D.; Sferrazza, M.; Williams, C.E. On the pearl size of hydrophobic polyelectrolytes. Europhys. Lett. 2003, 62, 110–116. [Google Scholar] [CrossRef] [Green Version]
- Spiteri, M.N.; Williams, C.E.; Boué, F. Pearl-Necklace-Like Chain Conformation of Hydrophobic Polyelectrolyte: A SANS Study of Partially Sulfonated Polystyrene in Water. Macromolecules 2007, 40, 6679–6691. [Google Scholar] [CrossRef] [Green Version]
- Essafi, W.; Lafuma, F.; Williams, C.E. Effect of Solvent Quality on the Behaviour of Highly Charged Polyelectrolytes. J. Phys. 1995, 5, 1269–1275. [Google Scholar] [CrossRef]
- Carbajal-Tinocco, M.D.; Williams, C.E. Static properties of hydrophobic polyelectrolytes in the thermodynamic limit. Europhys. Lett. 2000, 52, 284–290. [Google Scholar] [CrossRef]
- Manning, G.S. Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions I. Colligative Properties. J. Chem. Phys. 1969, 51, 924–933. [Google Scholar] [CrossRef]
- Oosawa, F. Polyelectrolytes; M. Dekker: New York, NY, USA, 1971. [Google Scholar]
- Essafi, W.; Lafuma, F.; Baigl, D.; Williams, C.E. Anomalous counterion condensation in salt-free hydrophobic polyelectrolyte solutions: Osmotic pressure measurements. Europhys. Lett. 2005, 71, 938–944. [Google Scholar] [CrossRef]
- Gromer, A.; Rawiso, M.; Maaloum, M. Visualization of Hydrophobic Polyelectrolytes Using Atomic Force Microscopy in Solution. Langmuir 2008, 24, 8950–8953. [Google Scholar] [CrossRef] [PubMed]
- Essafi, W.; Lafuma, F.; Williams, C.E. Structure of polyelectrolyte solutions at intermediate charge densities. In Macro-ion Characterization. From Dilute Solutions to Complex Fluids; Schmitz, K.S., Ed.; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1994; Volume 548, pp. 278–286. [Google Scholar]
- Makowski, H.S.; Lundberg, R.D.; Singhal, G.S. Flexible Polymeric Compositions Comprising a Normally Plastic Polymer Sulfonated to about 0.2 to about 10 Mole % Sulfonate. U.S. Patent 3870841, 11 March 1975. [Google Scholar]
- Baigl, D.; Seery, T.A.P.; Williams, C.E. Preparation and Characterization of Hydrosoluble, Partially Charged Poly(styrenesulfonate)s of Various Controlled Charge Fractions and Chain Lengths. Macromolecules 2002, 35, 2318–2326. [Google Scholar] [CrossRef]
- Lorchat, P.; Konko, I.; Combet, J.; Jestin, J.; Johner, A.; Laschewski, A.; Obukhov, S.; Rawiso, M. New regime in polyelectrolyte solutions. EPL (Europhys. Lett.) 2014, 106, 28003. [Google Scholar] [CrossRef]
- Shen, X.-C.; Bao, L.; Zhang, Z.-L.; Liu, X.; Pang, D.-W.; Xu, J. A simple and effective sample preparation method for atomic force microscopy visualization of individual DNA molecules in situ. Mol. Biol. Rep. 2011, 38, 965–969. [Google Scholar] [CrossRef] [PubMed]
- Pastré, D.; Hamon, L.; Landousy, F.; Sorel, I.; David, M.-O.; Zozime, A.; Le Cam, E.; Piétrement, O. Anionic Polyelectrolyte Adsorption on Mica Mediated by Multivalent Cations: A Solution to DNA Imaging by Atomic Force Microscopy under High Ionic Strengths. Langmuir 2006, 22, 6651–6660. [Google Scholar] [CrossRef] [PubMed]
- Wiseman, T.; Williston, S.; Brandts, J.F.; Lin, L.N. Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal. Biochem. 1989, 179, 131–137. [Google Scholar] [CrossRef]
- Pierce, M.M.; Raman, C.S.; Nall, B.T. Isothermal titration calorimetry of protein-protein interactions. Methods 1999, 19, 213–221. [Google Scholar] [CrossRef] [Green Version]
- Aberkane, L.; Jasniewski, J.; Gaiani, C.; Scher, J.; Sanchez, C. Thermodynamic Characterization of Acacia Gum-β-Lactoglobulin Complex Coacervation. Langmuir 2010, 26, 12523–12533. [Google Scholar] [CrossRef]
- Brautigam, C.A. Fitting two- and three-site binding models to isothermal titration calorimetric data. Methods 2015, 76, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Colby, R.H. Structure and linear viscoelasticity of flexible polymer solutions: Comparison of polyelectrolyte and neutral polymer solutions. Rheol. Acta 2010, 49, 425–442. [Google Scholar] [CrossRef]
- Sedlák, M. What Can Be Seen by Static and Dynamic Light Scattering in Polyelectrolyte Solutions and Mixtures? Langmuir 1999, 15, 4045–4051. [Google Scholar] [CrossRef]
- Muthukumar, M. Ordinary–extraordinary transition in dynamics of solutions of charged macromolecules. Proc. Natl. Acad. Sci. USA 2016, 113, 12627–12632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sedlák, M. Dynamic light scattering from binary mixtures of polyelectrolytes. II. Appearance of the medium polyelectrolyte mode upon mixing and comparison with experiments on binary mixtures of neutral polymers. J. Chem. Phys. 1997, 107, 10805. [Google Scholar] [CrossRef]
- Balding, P.; Borrelli, R.; Volkovinsky, R.; Russo, P.S. Physical Properties of Sodium Poly(styrene sulfonate): Comparison to Incompletely Sulfonated Polystyrene. Macromolecules 2022, 55, 1747–1762. [Google Scholar] [CrossRef]
- Balding, P.; Cueto, R.; Russo, P.S.; Gutekunst, W.R. Synthesis of perfectly sulfonated sodium polystyrene sulfonate over a wide molar mass range via reversible-deactivation radical polymerization. J. Polym. Sci. Polym. Chem. 2019, 57, 1527–1537. [Google Scholar] [CrossRef]
- Stradner, A.; Sedgwick, H.; Cardinaux, F.; Poon, W.C.; Egelhaaf, S.U.; Schurtenberger, P. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature 2004, 432, 492–495. [Google Scholar] [CrossRef] [Green Version]
- Pandav, G.; Pryamitsyn, V.; Ganesan, V. Interactions and Aggregation of Charged Nanoparticles in Uncharged Polymer Solutions. Langmuir 2015, 31, 12328–12338. [Google Scholar] [CrossRef]
- Starchenko, V.; Müller, M.; Lebovka, N. Growth of polyelectrolyte complex nanoparticles: Computer simulations and experiments. J. Phys. Chem. 2008, 112, 8863–8869. [Google Scholar] [CrossRef]
- Qi, L.; Fresnais, J.; Berret, J.-F.; Castaing, J.-C.; Grillo, I.; Chapel, J.-P. Influence of the Formulation Process in Electrostatic Assembly of Nanoparticles and Macromolecules in Aqueous Solution: The Mixing Pathway. J. Phys. Chem. 2010, 114, 12870–12877. [Google Scholar] [CrossRef]
- Qi, L.; Fresnais, J.; Berret, J.-F.; Chapel, J.-P. Influence of the formulation process in electrostatic assembly of nanoparticles and macromolecules in aqueous solution: The interaction pathway. J. Phys. Chem. 2010, 114, 16373–16381. [Google Scholar] [CrossRef]
- Dautzenberg, H. Polyelectrolyte complex formation in highly aggregating systems: Methodical aspects and general tendencies. In Physical Chemistry of Polyelectrolytes; Radeva, T., Ed.; Surfactant Science Series; Marcel Dekker: New York, NY, USA, 2001; Volume 99, pp. 743–792. [Google Scholar]
- Yuana, Y.; Gaoa, J.; Zhaia, Y.; Li, D.; Fu, C.; Huanga, Y. Mixing efficiency affects the morphology and compactness of chitosan/tripolyphosphate nanoparticles. Carbohydr. Polym. 2022, 287, 119331. [Google Scholar] [CrossRef] [PubMed]
- Ryde, N. Re: Do Polymer Molecules Have Zeta Potential? 2014. Available online: https://www.researchgate.net/post/Do_polymer_molecules_have_zeta_potential/53665293d3df3e80648b456d/citation/download (accessed on 29 April 2022).
- Oshima, H. Electrophoresis of Charged Particles and Drops. In Interfacial Electrokinetics and Electrophoresis; Delgado, A.V., Ed.; Surfactant science series; Marcel Dekker: New York, NY, USA, 2002; Volume 106, pp. 123–146. [Google Scholar]
- Vitorazi, L.; Ould-Moussa, N.; Sekar, S.; Fresnais, J.; Loh, W.; Chapel, J.-P.; Berret, J.-F. Evidence of a two-step process and pathway dependency in the thermodynamics of poly(diallyldimethylammonium chloride)/poly(sodium acrylate) complexation. Soft Matter 2014, 10, 9496–9505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delas, T.; Mock-Joubert, M.; Faivre, J.; Hofmaier, M.; Sandre, O.; Dole, F.; Chapel, J.-P.; Crépet, A.; Trombotto, S.; Delair, T.; et al. Effects of Chain Length of Chitosan Oligosaccharides on Solution Properties and Complexation with siRNA. Polymers 2019, 11, 1236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ou, Z.; Muthukumar, M. Entropy and enthalpy of polyelectrolyte complexation: Langevin dynamics Simulations. J. Chem. Phys. 2006, 124, 154902–154911. [Google Scholar] [CrossRef] [PubMed]
- Konko, I. Aqueous Solutions of Complexes Formed by Model Polyelectrolytes of Opposite Charges. Doctoral Dissertation, University of Strasbourg, Alsace, France, 2015. [Google Scholar]
- Michaels, A.S.; Mir, L.; Schneider, N.S. A Conductometric Study of Polycation—Polyanion Reactions in Dilute Aqueous Solution. J. Phys. Chem. 1965, 69, 1447–1455. [Google Scholar] [CrossRef]
- Pal, M.K.; Chaudhuri, M. Conductometric titrations of anionic polyelectrolytes with metachromatic dyes and effects of organic solvents. Die Makromol. Chem. Macromol. Chem. Phys. 1970, 133, 151–160. [Google Scholar] [CrossRef]
- Terayama, H. Method of colloid titration (a new titration between polymer ions). J. Polym. Sci. 1952, 8, 243–253. [Google Scholar] [CrossRef]
- Horn, D.; Heuck, C.C. Charge determination of proteins with polyelectrolyte titration. J. Biol. Chem. 1983, 258, 1665–1670. [Google Scholar] [CrossRef]
- Ben Fradj, A.; Lafi, R.; Gzara, L.; Hamzaoui, A.H.; Hafiane, A. Spectrophotometric study of the interaction of toluidine blue with poly (ammonium acrylate). J. Mol. Liq. 2014, 194, 110–114. [Google Scholar] [CrossRef]
- Vleugels, L.F.W.; Ricois, S.; Voets, I.K.; Tuinier, R. Reversal of metachromasy revisited; displacement of Toluidine-blue from alginate by surfactants. Colloids Surf. Physicochem. Eng. Asp. 2017, 529, 454–461. [Google Scholar] [CrossRef]
- Ben Mahmoud, S.; Hamzaoui, A.H.; Essafi, W. Spectrophotometric study of the interaction of methylene blue with poly (styrene-co-sodium styrene sulfonate). Mediterr. J. Chem. 2016, 5, 493–506. [Google Scholar] [CrossRef]
- Yusa, S.-I. Self-Assembly of Cholesterol-Containing Water-Soluble Polymers. Int. J. Polym. Sci. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Lee, K.Y.; Jo, W.H.; Kwon, I.C.; Kim, Y.-H.; Jeong, S.Y. Structural Determination and Interior Polarity of Self-Aggregates Prepared from Deoxycholic Acid-Modified Chitosan in Water. Macromolecules 1998, 31, 378–383. [Google Scholar] [CrossRef]
- Baigl, D. Etude Expérimentale de Polyélectrolytes Hydrophobes Modèles. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2003. [Google Scholar]










| Polymer | Charge | Mw (kDa) | N | f (%) | b1 (nm) | b2 (nm) b | Name |
|---|---|---|---|---|---|---|---|
| PDADMAC | + | ≤100 | 619 | 100 | 0.47 a | PDADMAC | |
| P(St-co-SSNa) | − | 400 | 2692 | 45 | 0.56 | 0.80 | PSS45% |
| P(St-co-SSNa) | − | 450 | 2692 | 64 | 0.39 | 0.78 | PSS64% |
| P(St-co-SSNa) | − | 500 | 2692 | 83 | 0.30 | 0.77 | PSS83% |
| P(St-co-SSNa) | − | 550 | 2692 | 100 | 0.25 | 0.58 | PSS100% |
| Primary Process | n | K (M−1) | ΔG (kJ mol−1) | ΔH (kJ mol−1) | TΔS (kJ mol−1) |
| PSS100% | 1.06 | 1.70.106 | −35.56 | −8.66 | 26.90 |
| PSS83% | 1.10 | 1.39.106 | −35.06 | −8.02 | 27.04 |
| PSS64% | 1.01 | 1.21.106 | −34.73 | −7.50 | 27.23 |
| PSS45% | 1.02 | 7.39.105 | −33.50 | −6.04 | 27.46 |
| Secondary Process | n | K (M−1) | ΔG (kJ mol−1) | ΔH (kJ mol−1) | TΔS (kJ mol−1) |
| PSS100% | 1.08 | 3.23.105 | −31.44 | 7.00 | 38.44 |
| PSS83% | 1.13 | 2.87.105 | −31.14 | 5.94 | 37.08 |
| PSS64% | 1.07 | 5.55.105 | −32.79 | 5.60 | 38.39 |
| PSS45% | 1.07 | 5.68.105 | −32.85 | 5.32 | 38.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jemili, N.; Fauquignon, M.; Grau, E.; Fatin-Rouge, N.; Dole, F.; Chapel, J.-P.; Essafi, W.; Schatz, C. Complexation in Aqueous Solution of a Hydrophobic Polyanion (PSSNa) Bearing Different Charge Densities with a Hydrophilic Polycation (PDADMAC). Polymers 2022, 14, 2404. https://doi.org/10.3390/polym14122404
Jemili N, Fauquignon M, Grau E, Fatin-Rouge N, Dole F, Chapel J-P, Essafi W, Schatz C. Complexation in Aqueous Solution of a Hydrophobic Polyanion (PSSNa) Bearing Different Charge Densities with a Hydrophilic Polycation (PDADMAC). Polymers. 2022; 14(12):2404. https://doi.org/10.3390/polym14122404
Chicago/Turabian StyleJemili, Nouha, Martin Fauquignon, Etienne Grau, Nicolas Fatin-Rouge, François Dole, Jean-Paul Chapel, Wafa Essafi, and Christophe Schatz. 2022. "Complexation in Aqueous Solution of a Hydrophobic Polyanion (PSSNa) Bearing Different Charge Densities with a Hydrophilic Polycation (PDADMAC)" Polymers 14, no. 12: 2404. https://doi.org/10.3390/polym14122404
APA StyleJemili, N., Fauquignon, M., Grau, E., Fatin-Rouge, N., Dole, F., Chapel, J. -P., Essafi, W., & Schatz, C. (2022). Complexation in Aqueous Solution of a Hydrophobic Polyanion (PSSNa) Bearing Different Charge Densities with a Hydrophilic Polycation (PDADMAC). Polymers, 14(12), 2404. https://doi.org/10.3390/polym14122404