Optimization of Printing Parameters to Maximize the Mechanical Properties of 3D-Printed PETG-Based Parts
Abstract
:1. Introduction
2. Materials and Methods
3. Design of Experiment Based on Taguchi Method
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernandez-Vicente, M.; Calle, W.; Ferrandiz, S.; Conejero, A. Effect of Infill Parameters on Tensile Mechanical Behavior in Desktop 3D Printing. 3D Print. Addit. Manuf. 2016, 3, 183–192. [Google Scholar] [CrossRef]
- Ćwikła, G.; Grabowik, C.; Kalinowski, K.; Paprocka, I.; Ociepka, P. The Influence of Printing Parameters on Selected Mechanical Properties of FDM/FFF 3D-Printed Parts. IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 012033. [Google Scholar] [CrossRef]
- Ruban, W.; Vijayakumar, V.; Dhanabal, P.; Pridhar, T. Effective Process Parameters in Selective Laser Sintering. Int. J. Rapid Manuf. 2014, 4, 148. [Google Scholar] [CrossRef]
- ISO/ASTM 52900:2015; Standard terminology for additive manufacturing—General Principles—Terminology. ASTM (American Society for Testing and Materials) International: West Conshohocken, PA, USA, 2015.
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric Appraisal of Mechanical Property of Fused Deposition Modelling Processed Parts. Mater. Des. 2010, 31, 287–295. [Google Scholar] [CrossRef]
- Jaisingh Sheoran, A.; Kumar, H. Fused Deposition Modeling Process Parameters Optimization and Effect on Mechanical Properties and Part Quality: Review and Reflection on Present Research. Mater. Today Proc. 2020, 21, 1659–1672. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of Fused Deposition Modeling Process Parameters: A Review of Current Research and Future Prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Stansbury, J.W.; Idacavage, M.J. 3D Printing with Polymers: Challenges among Expanding Options and Opportunities. Dent. Mater. 2016, 32, 54–64. [Google Scholar] [CrossRef]
- Torres, J.; Cotelo, J.; Karl, J.; Gordon, A.P. Mechanical Property Optimization of FDM PLA in Shear with Multiple Objectives. JOM 2015, 67, 1183–1193. [Google Scholar] [CrossRef]
- Wu, H.; Fahy, W.P.; Kim, S.; Kim, H.; Zhao, N.; Pilato, L.; Kafi, A.; Bateman, S.; Koo, J.H. Recent Developments in Polymers/Polymer Nanocomposites for Additive Manufacturing. Prog. Mater. Sci. 2020, 111, 100638. [Google Scholar] [CrossRef]
- Popescu, D.; Zapciu, A.; Amza, C.; Baciu, F.; Marinescu, R. FDM Process Parameters Influence over the Mechanical Properties of Polymer Specimens: A Review. Polym. Test. 2018, 69, 157–166. [Google Scholar] [CrossRef]
- Wach, R.A.; Wolszczak, P.; Adamus-Wlodarczyk, A. Enhancement of Mechanical Properties of FDM-PLA Parts via Thermal Annealing. Macromol. Mater. Eng. 2018, 303, 1800169. [Google Scholar] [CrossRef]
- Hong, J.-H.; Yu, T.; Chen, Z.; Park, S.-J.; Kim, Y.-H. Improvement of Flexural Strength and Compressive Strength by Heat Treatment of PLA Filament for 3D-Printing. Mod. Phys. Lett. B 2019, 33, 1940025. [Google Scholar] [CrossRef]
- Bhandari, S.; Lopez-Anido, R.A.; Gardner, D.J. Enhancing the Interlayer Tensile Strength of 3D Printed Short Carbon Fiber Reinforced PETG and PLA Composites via Annealing. Addit. Manuf. 2019, 30, 100922. [Google Scholar] [CrossRef]
- Sathish Kumar, K.; Soundararajan, R.; Shanthosh, G.; Saravanakumar, P.; Ratteesh, M.; Kumar, K.S.; Soundararajan, R.; Shanthosh, G.; Saravanakumar, P.; Ratteesh, M.; et al. Augmenting Effect of Infill Density and Annealing on Mechanical Properties of PETG and CFPETG Composites Fabricated by FDM. Mater. Today Proc. 2021, 45, 2186–2191. [Google Scholar] [CrossRef]
- Kasmi, S.; Ginoux, G.; Allaoui, S.; Alix, S. Investigation of 3D Printing Strategy on the Mechanical Performance of Coextruded Continuous Carbon Fiber Reinforced PETG. J. Appl. Polym. Sci. 2021, 138, 50955. [Google Scholar] [CrossRef]
- Jiang, D.; Smith, D.E. Anisotropic Mechanical Properties of Oriented Carbon Fiber Filled Polymer Composites Produced with Fused Filament Fabrication. Addit. Manuf. 2017, 18, 84–94. [Google Scholar] [CrossRef]
- Ferreira, I.; Vale, D.; Machado, M.; Lino, J. Additive Manufacturing of Polyethylene Terephthalate Glycol/Carbon Fiber Composites: An Experimental Study from Filament to Printed Parts. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 1866–1878. [Google Scholar] [CrossRef]
- Mansour, M.; Tsongas, K.; Tzetzis, D.; Antoniadis, A. Mechanical and Dynamic Behavior of Fused Filament Fabrication 3D Printed Polyethylene Terephthalate Glycol Reinforced with Carbon Fibers. Polym. Plast. Technol. Eng. 2018, 57, 1715–1725. [Google Scholar] [CrossRef]
- Valvez, S.; Silva, A.P.; Reis, P.N.B. Compressive Behaviour of 3D-Printed PETG Composites. Aerospace 2022, 9, 124. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive Manufacturing (3D Printing): A Review of Materials, Methods, Applications and Challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Bankupalli, N.; Srinivasa Rao, D.; Vamsi Krishna, T.S. Effect of Process Parameters and Butadiene Content on Friction and Wear Behaviour of ABS Components. Mater. Today Proc. 2019, 41, 416–421. [Google Scholar] [CrossRef]
- Song, X.; Shi, D.; Song, P.; Han, X.; Wei, Q.; Huang, C. Fused Deposition Modeling of Poly(Ether Ether Ketone) Scaffolds. High Temp. Mater. Process. 2021, 40, 1–11. [Google Scholar] [CrossRef]
- Wang, P.; Zou, B.; Xiao, H.; Ding, S.; Huang, C. Effects of Printing Parameters of Fused Deposition Modeling on Mechanical Properties, Surface Quality, and Microstructure of PEEK. J. Mater. Process. Technol. 2019, 271, 62–74. [Google Scholar] [CrossRef]
- Kumar, M.A.; Khan, M.S.; Mishra, S.B. Effect of Machine Parameters on Strength and Hardness of FDM Printed Carbon Fiber Reinforced PETG Thermoplastics. Mater. Today Proc. 2020, 27, 975–983. [Google Scholar] [CrossRef]
- Wang, P.; Pan, A.; Xia, L.; Cao, Y.; Zhang, H.; Wu, W. Effect of Process Parameters of Fused Deposition Modeling on Mechanical Properties of Poly-Ether-Ether-Ketone and Carbon Fiber/Poly-Ether-Ether-Ketone. High Perform. Polym. 2022, 34, 337–351. [Google Scholar] [CrossRef]
- Kovan, V.; Altan, G.; Topal, E.S. Effect of Layer Thickness and Print Orientation on Strength of 3D Printed and Adhesively Bonded Single Lap Joints. J. Mech. Sci. Technol. 2017, 31, 2197–2201. [Google Scholar] [CrossRef]
- Anitha, R.; Arunachalam, S.; Radhakrishnan, P. Critical Parameters Influencing the Quality of Prototypes in Fused Deposition Modelling. J. Mater. Process. Technol. 2001, 118, 385–388. [Google Scholar] [CrossRef]
- Nancharaiah, T.; Ranga Raju, D.; Ramachandra Raju, V. An Experimental Investigation on Surface Quality and Dimensional Accuracy of FDM Components. Int. J. Emerg. Technol. 2010, 1, 106–111. [Google Scholar]
- Gebisa, A.W.; Lemu, H.G. Investigating Effects of Fused-Deposition Modeling (FDM) Processing Parameters on Flexural Properties of ULTEM 9085 Using Designed Experiment. Materials 2018, 11, 500. [Google Scholar] [CrossRef] [Green Version]
- Ahn, S.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic Material Properties of Fused Deposition Modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef] [Green Version]
- Dawoud, M.; Taha, I.; Ebeid, S.J. Mechanical Behaviour of ABS: An Experimental Study Using FDM and Injection Moulding Techniques. J. Manuf. Process. 2016, 21, 39–45. [Google Scholar] [CrossRef]
- Johnson, G.A.; French, J.J. Evaluation of Infill Effect on Mechanical Properties of Consumer 3D Printing Materials. Adv. Technol. Innov. 2018, 3, 179–184. [Google Scholar]
- Raam Kumar, S.; Sridhar, S.; Venkatraman, R.; Venkatesan, M. Polymer Additive Manufacturing of ASA Structure: Influence of Printing Parameters on Mechanical Properties. Mater. Today Proc. 2020, 39, 1316–1319. [Google Scholar] [CrossRef]
- Nagaraj, C.; Mishra, D.; Tirupati, T. Optimization of the FDM Process Parameters to Attain the Desired Strength of ABS Specimens. Int. J. Recent Technol. Eng. 2019, 8, 1589–1593. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive Manufacturing of Carbon Fiber Reinforced Thermoplastic Composites Using Fused Deposition Modeling. Compos. Part B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Yang, C.; Tian, X.; Li, D.; Cao, Y.; Zhao, F.; Shi, C. Influence of Thermal Processing Conditions in 3D Printing on the Crystallinity and Mechanical Properties of PEEK Material. J. Mater. Process. Technol. 2017, 248, 1–7. [Google Scholar] [CrossRef]
- Ding, S.; Zou, B.; Wang, P.; Ding, H. Effects of Nozzle Temperature and Building Orientation on Mechanical Properties and Microstructure of PEEK and PEI Printed by 3D-FDM. Polym. Test. 2019, 78, 105948. [Google Scholar] [CrossRef]
- Berretta, S.; Davies, R.; Shyng, Y.T.; Wang, Y.; Ghita, O. Fused Deposition Modelling of High Temperature Polymers: Exploring CNT PEEK Composites. Polym. Test. 2017, 63, 251–262. [Google Scholar] [CrossRef]
- Zhang, J.; Panwar, A.; Bello, D.; Jozokos, T.; Isaacs, J.A.; Barry, C.; Mead, J. The Effects of Recycling on the Properties of Carbon Nanotube-Filled Polypropylene Composites and Worker Exposures. Environ. Sci. Nano 2016, 3, 409–417. [Google Scholar] [CrossRef]
- Shin, M.; Seo, J.; Kim, S.; Yoo, Y. Rheological Investigations of PC/MWNT Composites. In Proceedings of the 18th International Conference on Composite Materials (ICCM), Jeju Island, Korea, 21–26 August 2011; pp. 21–26. [Google Scholar]
- Vanaei, H.R.; Raissi, K.; Deligant, M.; Shirinbayan, M.; Fitoussi, J.; Khelladi, S.; Tcharkhtchi, A. Toward the Understanding of Temperature Effect on Bonding Strength, Dimensions and Geometry of 3D-Printed Parts. J. Mater. Sci. 2020, 55, 14677–14689. [Google Scholar] [CrossRef]
- El Magri, A.; El Mabrouk, K.; Vaudreuil, S.; Chibane, H.; Touhami, M.E. Optimization of Printing Parameters for Improvement of Mechanical and Thermal Performances of 3D Printed Poly(Ether Ether Ketone) Parts. J. Appl. Polym. Sci. 2020, 137, 49087. [Google Scholar] [CrossRef]
- El Magri, A.; El Mabrouk, K.; Vaudreuil, S.; Ebn Touhami, M. Experimental Investigation and Optimization of Printing Parameters of 3D Printed Polyphenylene Sulfide through Response Surface Methodology. J. Appl. Polym. Sci. 2020, 138, 49625. [Google Scholar] [CrossRef]
- Geng, P.; Zhao, J.; Wu, W.; Ye, W.; Wang, Y.; Wang, S.; Zhang, S. Effects of Extrusion Speed and Printing Speed on the 3D Printing Stability of Extruded PEEK Filament. J. Manuf. Process. 2019, 37, 266–273. [Google Scholar] [CrossRef]
- Christiyan, K.G.J.; Chandrasekhar, U.; Venkateswarlu, K. A Study on the Influence of Process Parameters on the Mechanical Properties of 3D Printed ABS Composite. IOP Conf. Ser. Mater. Sci. Eng. 2016, 114, 012109. [Google Scholar] [CrossRef]
- Abeykoon, C.; Sri-Amphorn, P.; Fernando, A. Optimization of Fused Deposition Modeling Parameters for Improved PLA and ABS 3D Printed Structures. Int. J. Light. Mater. Manuf. 2020, 3, 284–297. [Google Scholar] [CrossRef]
- Wang, P.; Zuo, B.; Ding, S.; Li, L.; Huang, C. Effects of FDM-3D Printing Parameters on Mechanical Properties and Microstructure of CF/PEEK and GF/PEEK. Chinese J. Aeronaut. 2021, 34, 236–246. [Google Scholar] [CrossRef]
- Sun, Q.; Rizvi, G.M.; Bellehumeur, C.T.; Gu, P. Effect of Processing Conditions on the Bonding Quality of FDM Polymer Filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Banna, M.H.; Shirokoff, J.; Molgaard, J. Effects of Two Aqueous Acidic Solutions on Polyester and Bisphenol A Epoxy Vinyl Ester Resins. Mater. Sci. Eng. A 2011, 528, 2137–2142. [Google Scholar] [CrossRef]
- Valvez, S.; Santos, P.; Parente, J.M.; Silva, M.P.; Reis, P.N.B. 3D Printed Continuous Carbon Fiber Reinforced PLA Composites: A Short Review. Procedia Struct. Integr. 2020, 25, 394–399. [Google Scholar] [CrossRef]
- Newman, S.T.; Zhu, Z.; Dhokia, V.; Shokrani, A. Process Planning for Additive and Subtractive Manufacturing Technologies. CIRP Ann.-Manuf. Technol. 2015, 64, 467–470. [Google Scholar] [CrossRef]
- Mahesh, V.; Joseph, A.S.; Mahesh, V.; Harursampath, D.; Chethan, V.N. Investigation on the Mechanical Properties of Additively Manufactured PETG Composites Reinforced with OMMT Nanoclay and Carbon Fibers. Polym. Compos. 2021, 42, 2380–2395. [Google Scholar] [CrossRef]
- Walter, R.; Selzer, R.; Gurka, M.; Friedrich, K. Effect of Filament Quality, Structure, and Processing Parameters on the Properties of Fused Filament Fabricated Short Fiber-Reinforced Thermoplastics; Elsevier Inc.: Amsterdam, The Netherlands, 2020; ISBN 9780128195352. [Google Scholar]
- Carneiro, O.S.; Silva, A.F.; Gomes, R. Fused Deposition Modeling with Polypropylene. Mater. Des. 2015, 83, 768–776. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S.; Nouri, H. Printability and Tensile Performance of 3D Printed Polyethylene Terephthalate Glycol Using Fused Deposition Modelling. Polymers 2019, 11, 1220. [Google Scholar] [CrossRef] [Green Version]
- Stepashkin; Chukov, D.I.; Senatov, F.S.; Salimon, A.I.; Korsunsky, A.M.; Kaloshkin, S.D. 3D-Printed PEEK-Carbon Fiber (CF) Composites: Structure and Thermal Properties. Compos. Sci. Technol. 2018, 164, 319–326. [Google Scholar] [CrossRef]
- Ferreira, I.; Melo, C.; Neto, R.; Machado, M.; Alves, J.L.; Mould, S. Study of the Annealing Influence on the Mechanical Performance of PA12 and PA12 Fibre Reinforced FFF Printed Specimens. Rapid Prototyp. J. 2020, 26, 1761–1770. [Google Scholar] [CrossRef]
- Pazhamannil, R.V.; Krishnan, C.N.; Edacherian, A. Investigations into the Effect of Thermal Annealing on Fused Filament Fabrication Process. Adv. Mater. Process. Technol. 2021. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, X.; Luo, T. Polymer Nanofibers with Outstanding Thermal Conductivity and Thermal Stability: Fundamental Linkage between Molecular Characteristics and Macroscopic Thermal Properties. J. Phys. Chem. C 2014, 118, 21148–21159. [Google Scholar] [CrossRef] [Green Version]
- Tirado-Garcia, I.; Garcia-Gonzalez, D.; Garzon-Hernandez, S.; Rusinek, A.; Robles, G.; Martinez-Tarifa, J.M.; Arias, A. Conductive 3D Printed PLA Composites: On the Interplay of Mechanical, Electrical and Thermal Behaviours. Compos. Struct. 2021, 265, 113744. [Google Scholar] [CrossRef]
- Yang, L.; Li, S.; Zhou, X.; Liu, J.; Li, Y.; Yang, M.; Yuan, Q.; Zhang, W. Effects of Carbon Nanotube on the Thermal, Mechanical, and Electrical Properties of PLA/CNT Printed Parts in the FDM Process. Synth. Met. 2019, 253, 122–130. [Google Scholar] [CrossRef]
- Composite Envisions Back to Basics: Carbon Fiber vs Fiberglass vs Kevlar/Aramid. Available online: https://compositeenvisions.com/back-to-basics-carbon-fiber-vs-fiberglass-vs-kevlararamid/ (accessed on 31 December 2021).
- Zhou, J.; Zhang, J.; Sang, M.; Liu, S.; Yuan, F.; Wang, S.; Sun, S.; Gong, X. Advanced Functional Kevlar Composite with Excellent Mechanical Properties for Thermal Management and Intelligent Safeguarding. Chem. Eng. J. 2022, 428, 131878. [Google Scholar] [CrossRef]
- George, K.; Mohanty, S.; Biswal, M.; Nayak, S.K. Thermal Insulation Behaviour of Ethylene Propylene Diene Monomer Rubber/Kevlar Fiber Based Hybrid Composites Containing Nanosilica for Solid Rocket Motor Insulation. J. Appl. Polym. Sci. 2021, 138, 49934. [Google Scholar] [CrossRef]
- Sousa, A.M.; Pinho, A.C.; Piedade, A.P. Mechanical Properties of 3D Printed Mouthguards: Influence of Layer Height and Device Thickness. Mater. Des. 2021, 203, 109624. [Google Scholar] [CrossRef]
- Gomez-Gras, G.; Jerez-Mesa, R.; Travieso-Rodriguez, J.A.; Lluma-Fuentes, J. Fatigue Performance of Fused Filament Fabrication PLA Specimens. Mater. Des. 2018, 140, 278–285. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, C.A.; Howarth, J.; De Almeida-Rowbotham, G.; Rees, A. A Design of Experiments Approach to Optimise Tensile and Notched Bending Properties of Fused Deposition Modelling Parts. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 1502–1512. [Google Scholar] [CrossRef]
- Lee, B.H.; Abdullah, J.; Khan, Z.A. Optimization of Rapid Prototyping Parameters for Production of Flexible ABS Object. J. Mater. Process. Technol. 2005, 169, 54–61. [Google Scholar] [CrossRef]









| Factor | Factor Code | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| Nozzle Temperature (°C) | A | 225 | 235 | 245 | 255 | 265 |
| Speed (mm/s) | B | 20 | 30 | 40 | 50 | 60 |
| Layer height (mm) | C | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 |
| Infill (%) | D | 20 | 40 | 60 | 80 | 100 |
| Factor | Factor Code | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| Nozzle Temperature (°C) | A | 195 | 205 | 215 | 235 | 245 |
| Speed (mm/s) | B | 20 | 30 | 40 | 50 | 60 |
| Layer height (mm) | C | 0.35 | 0.4 | 0.45 | 0.5 | 0.55 |
| Infill (%) | D | 20 | 40 | 60 | 80 | 100 |
| Factor | Factor Code | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| Nozzle Temperature (°C) | A | 235 | 245 | 255 | 260 | 265 |
| Speed (mm/s) | B | 20 | 30 | 40 | 50 | 60 |
| Layer height (mm) | C | 0.35 | 0.4 | 0.45 | 0.5 | 0.55 |
| Infill (%) | D | 20 | 40 | 60 | 80 | 100 |
| Run | A | B | C | D | Bending Stress (MPa) | Bending Modulus (GPa) | Bending Strain (%) |
|---|---|---|---|---|---|---|---|
| 1 | 225 | 20 | 0.2 | 20 | 30.75 ± 1.44 | 1.04 ± 0.07 | 3.64 ± 0.50 |
| 2 | 225 | 30 | 0.25 | 40 | 37.05 ± 3.64 | 1.13 ± 0.07 | 4.11 ± 0.48 |
| 3 | 225 | 40 | 0.3 | 60 | 46.95 ± 1.67 | 1.33 ± 0.07 | 4.76 ± 0.09 |
| 4 | 225 | 50 | 0.35 | 80 | 55.04 ± 2.34 | 1.30 ± 0.09 | 5.04 ± 0.20 |
| 5 | 225 | 60 | 0.4 | 100 | 63.14 ± 2.31 | 1.66 ± 0.11 | 5.47 ± 0.18 |
| 6 | 235 | 20 | 0.25 | 60 | 49.62 ± 1.87 | 1.38 ± 0.04 | 4.97 ± 0.09 |
| 7 | 235 | 30 | 0.3 | 80 | 55.10 ± 2.38 | 1.52 ± 0.05 | 5.52 ± 0.06 |
| 8 | 235 | 40 | 0.35 | 100 | 61.11 ± 4.02 | 1.64 ± 0.09 | 5.70 ± 0.06 |
| 9 | 235 | 50 | 0.4 | 20 | 35.74 ± 2.27 | 1.17 ± 0.05 | 4.02 ± 0.44 |
| 10 | 235 | 60 | 0.2 | 40 | 35.91 ± 1.29 | 1.12 ± 0.11 | 4.04 ± 0.35 |
| 11 | 245 | 20 | 0.3 | 100 | 66.66 ± 1.99 | 1.71 ± 0.08 | 5.55 ± 0.12 |
| 12 | 245 | 30 | 0.35 | 20 | 38.60 ± 4.02 | 1.20 ± 0.05 | 4.08 ± 0.09 |
| 13 | 245 | 40 | 0.4 | 40 | 46.70 ± 2.41 | 1.35 ± 0.11 | 4.42 ± 0.45 |
| 14 | 245 | 50 | 0.2 | 60 | 46.38 ± 1.33 | 1.31 ± 0.43 | 4.64 ± 0.05 |
| 15 | 245 | 60 | 0.25 | 80 | 54.48 ± 1.71 | 1.45 ± 0.06 | 5.10 ± 0.11 |
| 16 | 255 | 20 | 0.35 | 40 | 49.38 ± 2.42 | 1.39 ± 0.12 | 4.68 ± 0.13 |
| 17 | 255 | 30 | 0.4 | 60 | 57.47 ± 1.90 | 1.54 ± 0.11 | 5.18 ± 0.25 |
| 18 | 255 | 40 | 0.2 | 80 | 57.16 ± 1.39 | 1.49 ± 0.07 | 5.46 ± 0.17 |
| 19 | 255 | 50 | 0.25 | 100 | 65.05 ± 1.56 | 1.62 ± 0.09 | 5.76 ± 0.10 |
| 20 | 255 | 60 | 0.3 | 20 | 35.36 ± 1.09 | 1.13 ± 0.03 | 3.98 ± 0.23 |
| 21 | 265 | 20 | 0.4 | 80 | 53.56 ± 2.83 | 1.36 ± 0.09 | 5.61 ± 0.12 |
| 22 | 265 | 30 | 0.2 | 100 | 67.07 ± 1.43 | 1.69 ± 0.06 | 5.44 ± 0.26 |
| 23 | 265 | 40 | 0.25 | 20 | 33.62 ± 0.65 | 1.17 ± 0.02 | 4.09 ± 0.21 |
| 24 | 265 | 50 | 0.3 | 40 | 42.83 ± 1.52 | 1.26 ± 0.06 | 4.64 ± 0.19 |
| 25 | 265 | 60 | 0.35 | 60 | 52.59 ± 2.46 | 1.42 ± 0.09 | 5.22 ± 0.14 |
| Run | A | B | C | D | Bending Stress (MPa) | Bending Modulus (GPa) | Bending Strain (%) |
|---|---|---|---|---|---|---|---|
| 1 | 195 | 20 | 0.35 | 20 | 61.31 ± 3.48 | 2.94 ± 0.50 | 4.08 ± 0.94 |
| 2 | 195 | 30 | 0.4 | 40 | 64.53 ± 6.34 | 3.07 ± 0.32 | 4.79 ± 0.14 |
| 3 | 195 | 40 | 0.45 | 60 | 68.57 ± 1.79 | 2.67 ± 1.20 | 5.29 ± 0.04 |
| 4 | 195 | 50 | 0.5 | 80 | 71.99 ± 4.42 | 3.52 ± 0.24 | 5.89 ± 0.29 |
| 5 | 195 | 60 | 0.55 | 100 | 60.12 ± 2.32 | 2.80 ± 0.17 | 6.83 ± 0.31 |
| 6 | 205 | 20 | 0.4 | 60 | 64.13 ± 6.61 | 3.11 ± 0.31 | 4.98 ± 0.21 |
| 7 | 205 | 30 | 0.45 | 80 | 72.75 ± 2.53 | 3.17 ± 0.28 | 6.12 ± 0.12 |
| 8 | 205 | 40 | 0.5 | 100 | 69.76 ± 1.40 | 2.95 ± 0.12 | 5.91 ± 0.07 |
| 9 | 205 | 50 | 0.55 | 20 | 50.32 ± 2.42 | 2.18 ± 0.16 | 5.61 ± 0.08 |
| 10 | 205 | 60 | 0.35 | 40 | 63.63 ± 1.65 | 3.21 ± 0.09 | 4.71 ± 0.04 |
| 11 | 215 | 20 | 0.45 | 100 | 68.13 ± 4.02 | 3.03 ± 0.15 | 6.26 ± 0.04 |
| 12 | 215 | 30 | 0.5 | 20 | 49.63 ± 0.92 | 2.24 ± 0.07 | 4.93 ± 0.10 |
| 13 | 215 | 40 | 0.55 | 40 | 50.69 ± 0.82 | 2.19 ± 0.07 | 5.60 ± 0.21 |
| 14 | 215 | 50 | 0.35 | 60 | 63.22 ± 1.45 | 2.97 ± 0.11 | 4.99 ± 0.07 |
| 15 | 215 | 60 | 0.4 | 80 | 66.36 ± 1.15 | 2.89 ± 0.09 | 5.66 ± 0.04 |
| 16 | 235 | 20 | 0.5 | 40 | 44.17 ± 1.81 | 1.81 ± 0.18 | 5.30 ± 0.19 |
| 17 | 235 | 30 | 0.55 | 60 | 43.15 ± 1.67 | 1.66 ± 0.06 | 6.12 ± 0.09 |
| 18 | 235 | 40 | 0.35 | 80 | 58.74 ± 1.20 | 2.47 ± 0.06 | 5.70 ± 0.11 |
| 19 | 235 | 50 | 0.4 | 100 | 59.23 ± 1.22 | 2.40 ± 0.06 | 5.91 ± 0.12 |
| 20 | 235 | 60 | 0.45 | 20 | 40.60 ± 0.66 | 1.80 ± 0.11 | 5.24 ± 0.06 |
| 21 | 245 | 20 | 0.55 | 80 | 42.17 ± 1.79 | 1.54 ± 0.11 | 6.40 ± 0.15 |
| 22 | 245 | 30 | 0.35 | 100 | 64.58 ± 1.94 | 2.60 ± 0.14 | 6.16 ± 0.13 |
| 23 | 245 | 40 | 0.4 | 20 | 43.28 ± 2.31 | 1.92 ± 0.18 | 5.08 ± 0.18 |
| 24 | 245 | 50 | 0.45 | 40 | 46.39 ± 1.60 | 1.96 ± 0.08 | 5.59 ± 0.21 |
| 25 | 245 | 60 | 0.5 | 60 | 45.19 ± 1.69 | 1.70 ± 0.09 | 6.17 ± 0.19 |
| Run | A | B | C | D | Bending Stress (MPa) | Bending Modulus (GPa) | Bending Strain (%) |
|---|---|---|---|---|---|---|---|
| 1 | 235 | 20 | 0.35 | 20 | 30.91 ± 1.40 | 1.12 ± 0.11 | 7.02 ± 0.18 |
| 2 | 235 | 30 | 0.4 | 40 | 35.43 ± 0.92 | 1.22 ± 0.06 | 7.11 ± 0.12 |
| 3 | 235 | 40 | 0.45 | 60 | 39.24 ± 1.18 | 1.28 ± 0.07 | 7.83 ± 0.29 |
| 4 | 235 | 50 | 0.5 | 80 | 41.73 ± 1.03 | 1.29 ± 0.06 | 8.47 ± 0.22 |
| 5 | 235 | 60 | 0.55 | 100 | 39.82 ± 1.74 | 1.22 ± 0.09 | 8.86 ± 0.19 |
| 6 | 245 | 20 | 0.4 | 60 | 35.73 ± 1.06 | 1.25 ± 0.05 | 7.62 ± 0.17 |
| 7 | 245 | 30 | 0.45 | 80 | 38.81 ± 1.64 | 1.25 ± 0.06 | 8.86 ± 0.06 |
| 8 | 245 | 40 | 0.5 | 100 | 41.62 ± 5.77 | 1.33 ± 0.07 | 8.97 ± 0.17 |
| 9 | 245 | 50 | 0.55 | 20 | 30.33 ± 1.04 | 1.02 ± 0.05 | 7.42 ± 0.21 |
| 10 | 245 | 60 | 0.35 | 40 | 33.58 ± 0.40 | 1.21 ± 0.03 | 6.94 ± 0.08 |
| 11 | 255 | 20 | 0.45 | 100 | 44.65 ± 2.18 | 1.36 ± 0.10 | 9.08 ± 0.27 |
| 12 | 255 | 30 | 0.5 | 20 | 32.02 ± 0.95 | 1.12 ± 0.05 | 6.81 ± 0.21 |
| 13 | 255 | 40 | 0.55 | 40 | 34.28 ± 2.18 | 1.10 ± 0.08 | 7.91 ± 0.15 |
| 14 | 255 | 50 | 0.35 | 60 | 37.22 ± 0.78 | 1.25 ± 0.03 | 7.76 ± 0.13 |
| 15 | 255 | 60 | 0.4 | 80 | 39.62 ± 0.64 | 1.28 ± 0.03 | 8.55 ± 0.14 |
| 16 | 260 | 20 | 0.5 | 40 | 38.14 ± 0.70 | 1.15 ± 0.04 | 7.94 ± 0.17 |
| 17 | 260 | 30 | 0.55 | 60 | 38.06 ± 1.54 | 1.16 ± 0.07 | 8.52 ± 0.10 |
| 18 | 260 | 40 | 0.35 | 80 | 42.09 ± 1.05 | 1.36 ± 0.06 | 8.50 ± 0.27 |
| 19 | 260 | 50 | 0.4 | 100 | 40. 50 ± 1.42 | 1.26 ± 0.08 | 8.56 ± 0.19 |
| 20 | 260 | 60 | 0.45 | 20 | 29.20 ± 1.23 | 1.02 ± 0.07 | 7.55 ± 0.17 |
| 21 | 265 | 20 | 0.55 | 80 | 41.09 ± 2.67 | 1.22 ± 0.12 | 9.18 ± 0.21 |
| 22 | 265 | 30 | 0.35 | 100 | 47.35 ± 2.03 | 1.50 ± 0.07 | 9.12 ± 0.16 |
| 23 | 265 | 40 | 0.4 | 20 | 31.31 ± 0.95 | 1.15 ± 0.03 | 6.96 ± 0.09 |
| 24 | 265 | 50 | 0.45 | 40 | 35.02 ± 0.87 | 1.12 ± 0.06 | 7.77 ± 0.16 |
| 25 | 265 | 60 | 0.5 | 60 | 37.91 ± 0.80 | 1.15 ± 0.03 | 8.36 ± 0.15 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Remarks |
|---|---|---|---|---|---|---|
| Bending stress | ||||||
| Regression | 4 | 2761.19 | 690.30 | 86.65 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 73.00 | 73.00 | 9.16 | 0.007 | Significant |
| Speed (mm/s) | 1 | 14.80 | 14.80 | 1.86 | 0.188 | Insignificant |
| Layer height (mm) | 1 | 61.79 | 61.79 | 7.76 | 0.011 | Significant |
| Infill (%) | 1 | 2611.61 | 2611.61 | 327.84 | <0.001 | Significant |
| Error | 20 | 159.32 | 7.97 | |||
| Total | 24 | 2920.52 | ||||
| Bending modulus | ||||||
| Regression | 4 | 0.806934 | 0.201734 | 30.92 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 0.030027 | 0.030027 | 4.60 | 0.044 | Significant |
| Speed (mm/s) | 1 | 0.007923 | 0.007923 | 1.21 | 0.284 | Insignificant |
| Layer height (mm) | 1 | 0.021448 | 0.021448 | 3.29 | 0.085 | Insignificant |
| Infill (%) | 1 | 0.747536 | 0.747536 | 114.59 | <0.001 | Significant |
| Error | 20 | 0.130475 | 0.006524 | |||
| Total | 24 | 0.937410 | ||||
| Bending strain | ||||||
| Regression | 4 | 9.6222 | 2.40556 | 98.94 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 0.4574 | 0.45737 | 18.81 | <0.001 | Significant |
| Speed (mm/s) | 1 | 0.0446 | 0.04464 | 1.84 | 0.191 | Insignificant |
| Layer height (mm) | 1 | 0.2659 | 0.26588 | 10.94 | 0.004 | Significant |
| Infill (%) | 1 | 8.8543 | 8.85434 | 364.16 | <0.001 | Significant |
| Error | 20 | 0.4863 | 0.02431 | |||
| Total | 24 | 10.1085 | ||||
| Regression | 4 | 2761.19 | 690.30 | 86.65 | <0.001 | Significant |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Remarks |
|---|---|---|---|---|---|---|
| Bending stress | ||||||
| Regression | 4 | 2297.50 | 574.38 | 46.16 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 782.46 | 782.46 | 62.88 | <0.001 | Significant |
| Speed (mm/s) | 1 | 9.96 | 9.96 | 0.80 | 0.382 | Insignificant |
| Layer height (mm) | 1 | 182.68 | 182.68 | 14.68 | 0.001 | Significant |
| Infill (%) | 1 | 1322.40 | 1322.40 | 106.27 | <0.001 | Significant |
| Error | 20 | 248.87 | 12.44 | |||
| Total | 24 | 2546.37 | ||||
| Bending modulus | ||||||
| Regression | 4 | 6.51456 | 1.62864 | 43.49 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 4.03117 | 4.03117 | 107.64 | <0.001 | Significant |
| Speed (mm/s) | 1 | 0.00585 | 0.00585 | 0.16 | 0.697 | Insignificant |
| Layer height (mm) | 1 | 0.85626 | 0.85626 | 22.86 | <0.001 | Significant |
| Infill (%) | 1 | 1.62128 | 1.62128 | 43.29 | <0.001 | Significant |
| Error | 20 | 0.74904 | 0.03745 | |||
| Total | 24 | 7.26360 | ||||
| Bending strain | ||||||
| Regression | 4 | 4.17841 | 1.04460 | 66.78 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 1.73389 | 1.73389 | 110.84 | <0.001 | Significant |
| Speed (mm/s) | 1 | 0.00031 | 0.00031 | 0.02 | 0.889 | Insignificant |
| Layer height (mm) | 1 | 1.26760 | 1.26760 | 81.03 | <0.001 | Significant |
| Infill (%) | 1 | 1.17661 | 1.17661 | 75.22 | <0.001 | Significant |
| Error | 20 | 0.31286 | 0.01564 | |||
| Total | 24 | 4.49127 | ||||
| Regression | 4 | 2297.50 | 574.38 | 46.16 | <0.001 | Significant |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Remarks |
|---|---|---|---|---|---|---|
| Bending stress | ||||||
| Regression | 4 | 342.150 | 85.537 | 66.41 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 0.003 | 0.003 | 0.00 | 0.964 | Insignificant |
| Speed (mm/s) | 1 | 20.084 | 20.084 | 15.59 | 0.001 | Significant |
| Layer height (mm) | 1 | 0.029 | 0.029 | 0.02 | 0.882 | Insignificant |
| Infill (%) | 1 | 322.034 | 322.034 | 250.03 | <0.001 | Significant |
| Error | 20 | 25.759 | 1.288 | |||
| Total | 24 | 367.909 | ||||
| Bending modulus | ||||||
| Regression | 4 | 0.154184 | 0.038546 | 92.99 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 0.001158 | 0.001158 | 2.79 | 0.110 | Insignificant |
| Speed (mm/s) | 1 | 0.020467 | 0.020467 | 49.37 | <0.001 | Significant |
| Layer height (mm) | 1 | 0.029268 | 0.029268 | 70.61 | <0.001 | Significant |
| Infill (%) | 1 | 0.103291 | 0.103291 | 249.18 | <0.001 | Significant |
| Error | 20 | 0.008291 | 0.000415 | |||
| Total | 24 | 0.162474 | ||||
| Bending strain | ||||||
| Regression | 4 | 5.22057 | 1.30514 | 39.98 | <0.001 | Significant |
| Nozzle Temp. (°C) | 1 | 0.00668 | 0.00668 | 0.20 | 0.656 | Insignificant |
| Speed (mm/s) | 1 | 0.09363 | 0.09363 | 2.87 | 0.106 | Insignificant |
| Layer height (mm) | 1 | 0.35059 | 0.35059 | 10.74 | 0.004 | Significant |
| Infill (%) | 1 | 4.76967 | 4.76967 | 146.11 | <0.001 | Significant |
| Error | 20 | 0.65290 | 0.03265 | |||
| Total | 24 | 5.87347 |
| Response | S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|---|
| PETG | ||||
| Bending stress | 2.82244 | 94.54% | 93.45% | 90.29% |
| Bending modulus | 0.0807698 | 86.08% | 83.30% | 74.73% |
| Bending strain | 0.155930 | 95.19% | 94.23% | 92.35% |
| PETG+CF | ||||
| Bending stress | 3.52752 | 90.23% | 88.27% | 82.69% |
| Bending modulus | 0.193525 | 89.69% | 87.63% | 82.88% |
| Bending strain | 0.125072 | 93.03% | 91.64% | 89.42% |
| PETG+KF | ||||
| Bending stress | 1.13488 | 93.00% | 91.60% | 88.94% |
| Bending strain | 0.0203600 | 94.90% | 93.88% | 91.51% |
| Bending modulus | 0.180679 | 88.88% | 86.66% | 82.15% |
| Solution | Nozzle Temperature (°C) | Speed (mm/s) | Layer Height (mm) | Infill (%) | Bending Stress (MPa) Fit | Bending Modulus (GPa) Fit | Bending Strain (%) Fit | Composite Desirability |
|---|---|---|---|---|---|---|---|---|
| PETG | ||||||||
| 1 | 265.000 | 20.0000 | 0.400000 | 100.000 | 69.6761 | 1.73539 | 6.08315 | 0.99998 |
| 2 | 265.000 | 60.0000 | 0.400000 | 100.000 | 67.4999 | 1.68504 | 5.96363 | 0.98519 |
| 3 | 265.000 | 20.0000 | 0.200000 | 100.000 | 65.2296 | 1.65255 | 5.79147 | 0.95179 |
| 4 | 265.000 | 20.0000 | 0.201306 | 97.386 | 64.3140 | 1.63710 | 5.73837 | 0.93227 |
| 5 | 225.000 | 20.0000 | 0.400000 | 100.000 | 64.8431 | 1.63737 | 5.70059 | 0.93162 |
| 6 | 225.000 | 20.0000 | 0.400000 | 100.000 | 64.8431 | 1.63737 | 5.70058 | 0.93162 |
| 7 | 225.000 | 20.0000 | 0.400000 | 100.000 | 64.8431 | 1.63737 | 5.70058 | 0.93162 |
| 8 | 265.000 | 20.0000 | 0.400000 | 83.658 | 63.7709 | 1.63548 | 5.73931 | 0.92651 |
| 9 | 225.001 | 59.9997 | 0.400000 | 100.000 | 62.6669 | 1.58701 | 5.58107 | 0.86758 |
| 10 | 265.000 | 20.0000 | 0.400000 | 43.127 | 49.1245 | 1.38769 | 4.88649 | 0.53551 |
| PETG+CF | ||||||||
| 1 | 195.000 | 60.0000 | 0.525121 | 100.000 | 72.7516 | 3.18991 | 3.64024 | 0.802270 |
| 2 | 195.000 | 60.0000 | 0.525121 | 100.000 | 72.7516 | 3.18991 | 3.64024 | 0.802270 |
| 3 | 195.000 | 60.0000 | 0.550000 | 100.000 | 71.8005 | 3.12479 | 3.71947 | 0.800580 |
| 4 | 195.000 | 60.0000 | 0.550000 | 100.000 | 71.8005 | 3.12479 | 3.71947 | 0.800580 |
| 5 | 195.000 | 59.9938 | 0.550000 | 99.972 | 71.7932 | 3.12454 | 3.71926 | 0.800424 |
| 6 | 195.000 | 20.0000 | 0.511487 | 100.000 | 71.4874 | 3.18233 | 3.60680 | 0.782423 |
| 7 | 195.011 | 20.0000 | 0.550000 | 100.000 | 70.0117 | 3.08129 | 3.72960 | 0.779197 |
| 8 | 195.015 | 20.0000 | 0.550000 | 100.000 | 70.0105 | 3.08120 | 3.72966 | 0.779181 |
| 9 | 195.002 | 20.0000 | 0.350000 | 100.000 | 77.6602 | 3.60494 | 3.09257 | 0.687411 |
| 10 | 195.002 | 20.0000 | 0.350000 | 100.000 | 77.6602 | 3.60494 | 3.09257 | 0.687411 |
| PETG+KF | ||||||||
| 1 | 265.000 | 20.0000 | 0.350000 | 100.000 | 42.8514 | 1.38203 | 5.07710 | 0.896739 |
| 2 | 265.000 | 20.0000 | 0.478304 | 100.000 | 42.7895 | 1.31995 | 5.29197 | 0.882550 |
| 3 | 265.000 | 20.0000 | 0.550000 | 100.000 | 42.7548 | 1.28526 | 5.41204 | 0.859197 |
| 4 | 235.001 | 20.0000 | 0.550000 | 100.000 | 42.7263 | 1.26630 | 5.36653 | 0.834593 |
| 5 | 264.998 | 59.6749 | 0.350000 | 99.816 | 40.3135 | 1.30134 | 5.24594 | 0.795999 |
| 6 | 265.000 | 59.9983 | 0.350000 | 99.687 | 40.2768 | 1.30040 | 5.24536 | 0.794019 |
| 7 | 265.000 | 59.9983 | 0.350000 | 99.683 | 40.2762 | 1.30039 | 5.24530 | 0.793985 |
| 8 | 265.000 | 59.9981 | 0.350000 | 98.450 | 40.1198 | 1.29759 | 5.22626 | 0.783726 |
| 9 | 265.000 | 25.2370 | 0.350000 | 70.783 | 38.8121 | 1.30504 | 4.64857 | 0.635495 |
| 10 | 264.990 | 56.8432 | 0.350000 | 59.987 | 35.4390 | 1.21655 | 4.61860 | 0.470369 |
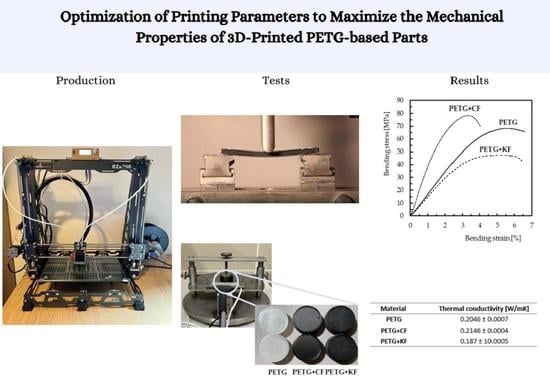
| Materials. | Condition | Bending Stress (MPa) | Bending Modulus (GPa) | Bending Strain (%) |
|---|---|---|---|---|
| PETG | Experimental | 66.9 ± 1.43 | 1.70 ± 0.025 | 5.66 ± 0.06 |
| Theoretical | 69.68 (−3.95%) | 1.74 (−2.3%) | 6.08 (−6.91%) | |
| PETG+CF | Experimental | 79.2 ± 0.97 | 3.55 ± 0.18 | 3.23 ± 0.21 |
| Theoretical | 72.75 (9.69%) | 3.19 (11.29%) | 3.64 (−11.26%) | |
| PETG+KF | Experimental | 47.7 ± 0.97 | 1.53 ± 0.27 | 5.10 ± 0.1 |
| Theoretical | 42.85 (11.32%) | 1.38 (10.87%) | 5.08 (0.39%) |
| Material | Thermal Conductivity (W/mK) |
|---|---|
| PETG | 0.2046 ± 0.0007 |
| PETG+CF | 0.2146 ± 0.0004 |
| PETG+KF | 0.187 ± 10.0005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valvez, S.; Silva, A.P.; Reis, P.N.B. Optimization of Printing Parameters to Maximize the Mechanical Properties of 3D-Printed PETG-Based Parts. Polymers 2022, 14, 2564. https://doi.org/10.3390/polym14132564
Valvez S, Silva AP, Reis PNB. Optimization of Printing Parameters to Maximize the Mechanical Properties of 3D-Printed PETG-Based Parts. Polymers. 2022; 14(13):2564. https://doi.org/10.3390/polym14132564
Chicago/Turabian StyleValvez, Sara, Abilio P. Silva, and Paulo N. B. Reis. 2022. "Optimization of Printing Parameters to Maximize the Mechanical Properties of 3D-Printed PETG-Based Parts" Polymers 14, no. 13: 2564. https://doi.org/10.3390/polym14132564
APA StyleValvez, S., Silva, A. P., & Reis, P. N. B. (2022). Optimization of Printing Parameters to Maximize the Mechanical Properties of 3D-Printed PETG-Based Parts. Polymers, 14(13), 2564. https://doi.org/10.3390/polym14132564