Thickness-Prediction Method Involving Tow Redistribution for the Dome of Composite Hydrogen Storage Vessels
Abstract
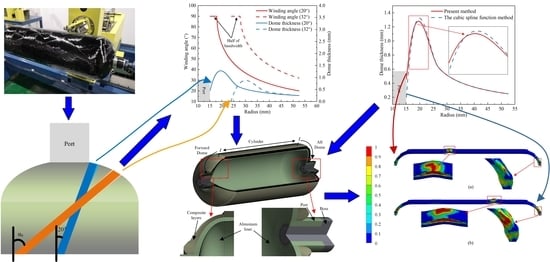
:1. Introduction
2. Analytical Model for Dome Thickness Prediction
2.1. Dome Thickness at Polar Openings
2.1.1. Dome Thickness before Reaming
2.1.2. Dome Thickness after Reaming
2.2. Revised Model of Radius Corresponding to Bandwidth
2.3. Revised Model of Fiber Volume within Two Bandwidths
2.4. Verification of the Analytical Model
3. Numerical Modeling
3.1. Winding Angle and Thickness
3.2. Layer-Up Design Schemes
3.3. Finite-Element Model
3.4. Progressive Damage Model
4. Results and Discussion
4.1. Load-Bearing Capacity and Damage Behavior
4.2. Damage-Evolution Laws
4.3. Stress Distribution of the Aluminum Liner
4.4. Comparison with the Cubic Spline Function Method
5. Conclusions
- (1)
- The maximum relative error of the predicted thickness was 4.19%, the mean absolute percentage error was 2.04%, and the root-mean-square error was 0.48 mm. The results verified that the predicted thickness of the present method was in good agreement with the actual measured thickness.
- (2)
- The results showed that the reaming process increased the burst pressure of the hydrogen storage vessel by 9.15%. The maximum stress of the aluminum liner under the working pressure was reduced by 19.15% after autofrettage, and the stress amplitude was reduced by 9.28%.
- (3)
- The stress concentration in the composite layers caused by fiber overhead was improved by changing the layer-up sequence as follows: the hoop and helical layers were separated, the winding angles of helical layers were changed from small to large, and the inner portion of the composite layers consisted of helical layers. The burst pressure of the vessel was increased by 7.88% compared with the traditional design sequence.
- (4)
- The burst pressures predicted by the two methods had little difference. However, the cubic spline function method underestimated the actual thickness of polar openings. The burst mode of the vessel predicted by the cubic spline function method was unsafe. The analysis results of the present method approached the actual case.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Son, D.S.; Chang, S.H. Evaluation of modeling techniques for a type III hydrogen pressure vessel (70 MPa) made of an aluminum liner and a thick carbon/epoxy composite for fuel cell vehicles. Int. J. Hydrogen Energy 2012, 37, 2353–2369. [Google Scholar] [CrossRef]
- Wang, X.; Lin, L.; Lu, S.; Zhang, L.; Li, B.; Zhang, D.; Luo, Y. Evaluation of embedded buckypaper sensors in composite overwrappedped pressure vessels for progressive damage monitoring. Compos. Struct. 2022, 284, 115223. [Google Scholar] [CrossRef]
- Ma, L.; He, J.; Gu, Y.; Zhang, Z.; Yu, Z.; Zhou, A.; Tam, L.H.; Wu, C. Structure design of gfrp composite leaf spring: An experimental and finite element analysis. Polymers 2021, 13, 1193. [Google Scholar] [CrossRef] [PubMed]
- Eggers, F.; Almeida, J.H.S.; Lisbôa, T.V.; Amico, S.C. Creep and residual properties of filament-wound composite rings under radial compression in harsh environments. Polymers 2021, 23, 33. [Google Scholar] [CrossRef]
- Mishra, R.; Behera, B.K.; Mukherjee, S.; Petru, M.; Muller, M. Axial and radial compression behavior of composite rocket launcher developed by robotized filament winding: Simulation and experimental validation. Polymers 2021, 13, 517. [Google Scholar] [CrossRef] [PubMed]
- Boon, Y.D.; Joshi, S.C.; Bhudolia, S.K. Review: Filament winding and automated fiber placement with in situ consolidation for fiber reinforced thermoplastic polymer composites. Polymers 2021, 13, 1951. [Google Scholar] [CrossRef] [PubMed]
- Kashyzadeh, K.R.; Koloor, S.S.R.; Bidgoli, M.O.; Petrů, M.; Asfarjani, A.A. An optimum fatigue design of polymer composite compressed natural gas tank using hybrid finite element-response surface methods. Polymers 2021, 13, 483. [Google Scholar] [CrossRef]
- Jiao, W.; Wang, R.; Liu, W.; Yang, F. Dome thickness prediction of composite pressure vessels. Fuhe Cailiao Xuebao (Acta Mater. Compos. Sin.) 2010, 27, 116–121. [Google Scholar]
- Krikanov, A.A. Refined thickness of filament wound shells. Sci. Eng. Compos. Mater. 2002, 10, 241–248. [Google Scholar] [CrossRef]
- Hartung, R.F. Planar-wound filamentary pressure vessels. AIAA J. 1963, 1, 2842–2844. [Google Scholar] [CrossRef]
- Wang, R.; Jiao, W.; Liu, W.; Yang, F. A new method for predicting dome thickness of composite pressure vessels. J. Reinf. Plast. Compos. 2010, 29, 3345–3352. [Google Scholar] [CrossRef]
- Wang, R.; Jiao, W.; Liu, W.; Yang, F. Dome thickness prediction of composite pressure vessels by a cubic spline function and finite element analysis. Polym. Polym. Compos. 2011, 19, 227–234. [Google Scholar] [CrossRef]
- Leh, D.; Saffré, P.; Francescato, P.; Arrieux, R. Multi-sequence dome lay-up simulations for hydrogen hyper-bar composite pressure vessels. Compos. Part A Appl. Sci. Manuf. 2013, 52, 106–117. [Google Scholar] [CrossRef]
- Zu, L.; Xu, H.; Jia, X.; Zhang, Q.; Wang, H.; Zhang, B. Winding path design based on mandrel profile updates of composite pressure vessels. Compos. Struct. 2020, 235, 111766. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, H.; Jia, X.; Zu, L.; Cheng, S.; Wang, H. Design of a 70 MPa type IV hydrogen storage vessel using accurate modeling techniques for dome thickness prediction. Compos. Struct. 2020, 236, 1–10. [Google Scholar] [CrossRef]
- Che, J.-l.; Han, M.G.; Chang, S.H. Prediction of composite layer thickness for Type III hydrogen pressure vessel at the dome part. Compos. Struct. 2021, 271, 114177. [Google Scholar] [CrossRef]
- Akhtar, M.K.; Qureshi, W.A.; Jamshed, R.; Raza, M. Analytical modeling and numerical analysis of the effect of mosaic patterns on composite pressure vessels with dome. J. Reinf. Plast. Compos. 2021, 40, 621–631. [Google Scholar] [CrossRef]
- Han, Z.; Li, H.; Xu, X.; Wang, H.; Li, H.; Tao, J. Crushing characteristics of aluminum/CFRP/aluminum hybrid tubes prepared by spinning forming. Compos. Struct. 2020, 249, 112551. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, M.; Pan, B. Simulation and burst validation of 70 MPa type IV hydrogen storage vessel with dome reinforcement. Int. J. Hydrogen Energy 2021, 46, 23779–23794. [Google Scholar] [CrossRef]
- Liao, B.-B.; Wang, D.-L.; Jia, L.-Y.; Zheng, J.-Y.; Gu, C.-H. Continuum damage modeling and progressive failure analysis of a Type III composite vessel by considering the effect of autofrettage. J. Zhejiang Univ. Sci. A 2019, 20, 36–49. [Google Scholar] [CrossRef]
- Kangal, S.; Kartav, O.; Tanoğlu, M.; Aktaş, E.; Artem, H.S. Investigation of interlayer hybridization effect on burst pressure performance of composite overwrapped pressure vessels with load-sharing metallic liner. J. Compos. Mater. 2020, 54, 961–980. [Google Scholar] [CrossRef]
- Lin, S.; Yang, L.; Xu, H.; Jia, X.; Yang, X.; Zu, L. Progressive damage analysis for multiscale modelling of composite pressure vessels based on Puck failure criterion. Compos. Struct. 2021, 255. [Google Scholar] [CrossRef]
- Alam, S.; Yandek, G.R.; Lee, R.C.; Mabry, J.M. Design and development of a filament wound composite overwrapped pressure vessel. Compos. Part C Open Access 2020, 2, 100045. [Google Scholar] [CrossRef]
- Sharma, P.; Bera, T.; Semwal, K.; Badhe, R.M.; Sharma, A.; Ramakumar, S.S.V.; Neogi, S. Theoretical analysis of design of filament wound type 3 composite cylinder for the storage of compressed hydrogen gas. Int. J. Hydrogen Energy 2020, 45, 25386–25397. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, M.H.; Zu, L.; Jia, X.; Shen, A.; Yang, Q.; Xu, K. Investigation on failure behaviors of 70 MPa Type IV carbon fiber overwound hydrogen storage vessels. Compos. Struct. 2021, 259, 1–11. [Google Scholar] [CrossRef]
- Weerts, R.A.J.; Cousigné, O.; Kunze, K.; Geers, M.G.D.; Remmers, J.J.C. Novel material model to predict the residual strength of a composite overwrapped pressure vessel after impact. Int. J. Impact Eng. 2022, 160. [Google Scholar] [CrossRef]
- Nguyen, B.N.; Roh, H.S.; Merkel, D.R.; Simmons, K.L. A predictive modeling tool for damage analysis and design of hydrogen storage composite pressure vessels. Int. J. Hydrogen Energy 2021, 46, 20573–20585. [Google Scholar] [CrossRef]
- Ahmadi Jebeli, M.; Heidari-Rarani, M. Development of Abaqus WCM plugin for progressive failure analysis of type IV composite pressure vessels based on Puck failure criterion. Eng. Fail. Anal. 2022, 131, 105851. [Google Scholar] [CrossRef]
- MathWorks. Available online: https://ww2.mathworks.cn/en/ (accessed on 1 December 2021).
- Gramoll, K.; Onoda, J.; Namiki, F. Dome thcikness of filament wound pressure vessels. Trans. Japan Soc. Aeronaut. Space Sci. 1990, 33, 69–79. [Google Scholar]
- Peters, S.T. Composite Filament Winding; ASM International: Cleveland, OH, USA, 2011; pp. 19–28. ISBN 978-1-61503-722-3. [Google Scholar]
- Puck, A.; Schürmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 2002, 62, 1633–1662. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. A progressive damage model for mechanically fastened joints in composite laminates. J. Compos. Mater. 1999, 33, 2248–2280. [Google Scholar] [CrossRef]





















| Vessel’s Type | Dome Length h (mm) | Fiber Band b (mm) | Thickness of Fiber Tows tp (mm) | Polar Radius r0 (mm) | Radius of Cylinder Section R (mm) |
|---|---|---|---|---|---|
| a | 80 | 5.39 | 0.765 | 9.5 | 132 |
| b | 213 | 5.39 | 0.765 | 60 | 132 |
| c | 213 | 12.5 | 0.48 | 110 | 372.5 |
| The Present Method | The Double Formula Method | The Cubic Spline Function Method | |||||
|---|---|---|---|---|---|---|---|
| r (mm) | Actual Thickness (mm) | Predicted Value (mm) | Relative Error (%) | Predicted Value (mm) | Relative Error (%) | Predicted Value (mm) | Relative Error (%) |
| 9.50 | 8.50 | 8.25 | −2.94 | 0 | - | 5.31 | - |
| 11.20 | 22.00 | 21.12 | −4.00 | 20.69 | −5.95 | 21.77 | −1.05 |
| 11.60 | 23.50 | 22.96 | −2.29 | 22.67 | −3.53 | 24.05 | 2.34 |
| 12.50 | 26.00 | 25.69 | −1.12 | 26.27 | 1.04 | 27.34 | 5.15 |
| 13.50 | 27.30 | 26.77 | −1.94 | 29.42 | 7.77 | 28.42 | 4.10 |
| 14.50 | 26.60 | 26.19 | −1.57 | 31.98 | 20.23 | 27.28 | 2.56 |
| 15.40 | 24.80 | 24.63 | −0.69 | 24.23 | −2.30 | 25.10 | 1.21 |
| 16.30 | 21.50 | 22.40 | 4.19 | 19.73 | −8.23 | 22.13 | 2.93 |
| 17.50 | 18.70 | 18.93 | 1.23 | 16.54 | −11.55 | 18.00 | −3.74 |
| 18.56 | 15.80 | 15.96 | 1.01 | 14.69 | −7.03 | 15.00 | −5.06 |
| 19.50 | 13.80 | 13.81 | 0.07 | 13.45 | −2.54 | 13.38 | −3.04 |
| 20.30 | 13.00 | 12.63 | −2.85 | 12.59 | −3.15 | 12.45 | −4.23 |
| Property | E (GPa) | μ | σs (MPa) | σb (MPa) | δ (%) | ρ (kg/m3) |
|---|---|---|---|---|---|---|
| 6061-T6 | 74.12 GPa | 0.28 | 340 | 281 | 11.57 | 2700 |
| Property | E11 * (GPa) | E22 * (GPa) | E33 * (GPa) | G12 (MPa) | G23 (MPa) | G13 (MPa) | μ12 | μ23 | μ13 |
|---|---|---|---|---|---|---|---|---|---|
| T700/epoxy composite | 134 | 7.42 | 7.42 | 3710 | 4790 | 3710 | 0.28 | 0.3 | 0.28 |
| Property | XT (MPa) | XC (MPa) | YT (MPa) | YC (MPa) | S12 (MPa) | S23 (MPa) | S13 (MPa) | ρ (kg/m3) |
|---|---|---|---|---|---|---|---|---|
| T700/epoxy composite | 2300 | 1250 | 74 | 180 | 50 | 90 | 50 | 1680 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Valve | 2300 | 1250 | 230 | 134 | 0.28 | 0.2 |
| (MPa) | (MPa) | (MPa) | ||||
| 74 | 50 | 180 | 0.3 | 0.3 | 0.35 |
| Failure Modes | Stiffness-Degradation Criteria |
|---|---|
| Fiber tensile failure | E11 = 0.07E11, E22 = E33 = 0.07E22, υ12 = υ13 = 0.07υ12, υ23 = 0.07υ23, G12 = G13 = 0.07G12, G23 = 0.07G23 |
| Fiber compression failure | E11 = 0.14E11, E22 = E33 = 0.14E22, υ12 = υ13 = 0.14υ12, υ23 = 0.14υ23, G12 = G13 = 0.14G12, G23 = 0.14G23 |
| Matrix tensile failure | E22 = 0.2E22, G12 = 0.2G12, G23 = 0.2G23 |
| Matrix compression failure | E22 = 0.4E22, G12 = 0.4G12, G23 = 0.4G23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Fu, S.; Chen, Y.; Hua, L. Thickness-Prediction Method Involving Tow Redistribution for the Dome of Composite Hydrogen Storage Vessels. Polymers 2022, 14, 902. https://doi.org/10.3390/polym14050902
Wang H, Fu S, Chen Y, Hua L. Thickness-Prediction Method Involving Tow Redistribution for the Dome of Composite Hydrogen Storage Vessels. Polymers. 2022; 14(5):902. https://doi.org/10.3390/polym14050902
Chicago/Turabian StyleWang, Hui, Shuang Fu, Yizhe Chen, and Lin Hua. 2022. "Thickness-Prediction Method Involving Tow Redistribution for the Dome of Composite Hydrogen Storage Vessels" Polymers 14, no. 5: 902. https://doi.org/10.3390/polym14050902
APA StyleWang, H., Fu, S., Chen, Y., & Hua, L. (2022). Thickness-Prediction Method Involving Tow Redistribution for the Dome of Composite Hydrogen Storage Vessels. Polymers, 14(5), 902. https://doi.org/10.3390/polym14050902