The Effect of Mechanical Elongation on the Thermal Conductivity of Amorphous and Semicrystalline Thermoplastic Polyimides: Atomistic Simulations
Abstract
:1. Introduction
2. Methodology
2.1. Objects of Study
2.2. Model and Simulation Techniques
2.2.1. Unordered Polyimide Samples
2.2.2. Mechanically Elongated Samples of Polyimides
2.2.3. Cooling down of Polyimide Samples from the Melt to the Glassy State
2.2.4. Calculation of the Thermal Conductivity Coefficient
3. Results and Discussion
3.1. Validation of GAFF Force Field for Computer Simulation of Polyimides
3.2. Influence of Deformation on the Thermal Conductivity Coefficient
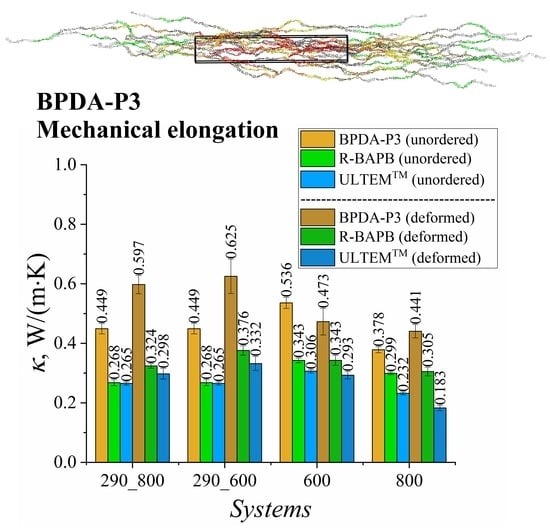
3.3. Comparison of the Influence of Polymer Ordering after Mechanical Elongation and Self-Ordering during Long Simulation on the Thermal Conductivity Coefficient of Semicrystalline Polyimide BPDA-P3
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moore, A.L.; Shi, L. Emerging challenges and materials for thermal management of electronics. Mater. Today 2014, 17, 163–174. [Google Scholar] [CrossRef]
- Yu, W.; Liu, C.; Qiu, L.; Zhang, P.; Ma, W.; Yue, Y.; Xie, H.; Larkin, L.S. Advanced Thermal Interface Materials for Thermal Management. Eng. Sci. 2018, 2, 1–3. [Google Scholar] [CrossRef]
- Razeeb, K.M.; Dalton, E.; Cross, G.L.W.; Robinson, A.J. Present and future thermal interface materials for electronic devices. Int. Mater. Rev. 2017, 63, 1–21. [Google Scholar] [CrossRef]
- Bar-Cohen, A.; Matin, K.; Narumanchi, S. Nanothermal Interface Materials: Technology Review and Recent Results. J. Electron. Packag. Trans. ASME 2015, 137, 010801. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Meng, F.; Li, D.; Tian, X.; Wang, Z.; Zhou, Z. Super-high thermal conductivity of polyamide-6/graphene-graphene oxide composites through in situ polymerization. High Perform. Polym. 2016, 29, 585–594. [Google Scholar] [CrossRef]
- Kim, G.-H.; Lee, D.; Shanker, A.; Shao, L.; Kwon, M.S.; Gidley, D.W.; Kim, J.; Pipe, K.P. High thermal conductivity in amorphous polymer blends by engineered interchain interactions. Nat. Mater. 2014, 14, 295–300. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Wang, X.; Zhou, J.; Song, B.; Jiang, Z.; Lee, E.M.Y.; Huberman, S.; Gleason, K.K.; Chen, G. Molecular engineered conjugated polymer with high thermal conductivity. Sci. Adv. 2018, 4, eaar3031. [Google Scholar] [CrossRef] [Green Version]
- Bessonov, M.I.; Koton, M.M.; Kudryavtsev, V.V.; Laius, L.A. Polyimides: Thermally Stable Polymers; Plenum: New York, NY, USA, 1987. [Google Scholar]
- Liaw, D.-J.; Wang, K.-L.; Huang, Y.-C.; Lee, K.-R.; Lai, J.-Y.; Ha, C.-S. Advanced polyimide materials: Syntheses, physical properties and applications. Prog. Polym. Sci. 2012, 37, 907–974. [Google Scholar] [CrossRef]
- Lyulin, S.V.; Larin, S.V.; Nazarychev, V.M.; Fal’kovich, S.G.; Kenny, J.M. Multiscale computer simulation of polymer nanocomposites based on thermoplastics. Polym. Sci. Ser. C 2016, 58, 2–15. [Google Scholar] [CrossRef]
- Hicyilmaz, A.S.; Bedeloglu, A.C. Applications of polyimide coatings: A review. SN Appl. Sci. 2021, 3, 363. [Google Scholar] [CrossRef]
- Polyimide Film Market Size, Share & Trends Analysis Report By Application (Flexible Printed Circuit, Wire & Cable, Pressure Sensitive Tape, Specialty Fabricated Product, Motor/Generator), by End-Use, by Region, and Segment Forecasts, 2023–2030. Available online: https://www.grandviewresearch.com/industry-analysis/polyimide-film-market (accessed on 28 June 2023).
- Morimune-Moriya, S.; Obara, K.; Fuseya, M.; Katanosaka, M. Development and characterization of strong, heat-resistant and thermally conductive polyimide/nanodiamond nanocomposites. Polymer 2021, 230, 124098. [Google Scholar] [CrossRef]
- Benford, D.J.; Powers, T.J.; Moseley, S.H. Thermal conductivity of Kapton tape. Cryogenics 1999, 39, 93–95. [Google Scholar] [CrossRef]
- Huang, C.; Qian, X.; Yang, R. Thermal conductivity of polymers and polymer nanocomposites. Mater. Sci. Eng. R Rep. 2018, 132, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Hao, H.; Hui, D.; Lau, D. Material advancement in technological development for the 5G wireless communications. Nanotechnol. Rev. 2020, 9, 683–699. [Google Scholar] [CrossRef]
- Lewis, J.S.; Perrier, T.; Barani, Z.; Kargar, F.; Balandin, A.A. Thermal interface materials with graphene fillers: Review of the state of the art and outlook for future applications. Nanotechnology 2021, 32, 142003. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Xu, G.; Yang, X.; Ruan, K.; Ma, T.; Zhang, Q.; Gu, J.; Wu, Y.; Liu, H.; Guo, Z. Significantly enhanced and precisely modeled thermal conductivity in polyimide nanocomposites with chemically modified graphene via in situ polymerization and electrospinning-hot press technology. J. Mater. Chem. C 2018, 6, 3004–3015. [Google Scholar] [CrossRef]
- Ning, W.; Wang, Z.; Liu, P.; Zhou, D.; Yang, S.; Wang, J.; Li, Q.; Fan, S.; Jiang, K. Multifunctional super-aligned carbon nanotube/polyimide composite film heaters and actuators. Carbon 2018, 139, 1136–1143. [Google Scholar] [CrossRef]
- He, X.; Wang, Y. Highly Thermally Conductive Polyimide Composite Films with Excellent Thermal and Electrical Insulating Properties. Ind. Eng. Chem. Res. 2020, 59, 1925–1933. [Google Scholar] [CrossRef]
- Tsai, M.-H.; Tseng, I.-H.; Chiang, J.-C.; Li, J.-J. Flexible Polyimide Films Hybrid with Functionalized Boron Nitride and Graphene Oxide Simultaneously To Improve Thermal Conduction and Dimensional Stability. ACS Appl. Mater. Interfaces 2014, 6, 8639–8645. [Google Scholar] [CrossRef]
- Ha, H.W.; Choudhury, A.; Kamal, T.; Kim, D.-H.; Park, S.-Y. Effect of Chemical Modification of Graphene on Mechanical, Electrical, and Thermal Properties of Polyimide/Graphene Nanocomposites. ACS Appl. Mater. Interfaces 2012, 4, 4623–4630. [Google Scholar] [CrossRef]
- Li, A.; Zhang, C.; Zhang, Y.-F. Thermal Conductivity of Graphene-Polymer Composites: Mechanisms, Properties, and Applications. Polymers 2017, 9, 437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ogbonna, V.E.; Popoola, A.P.I.; Popoola, O.M.; Adeosun, S.O. Recent progress on improving the mechanical, thermal and electrical conductivity properties of polyimide matrix composites from nanofillers perspective for technological applications. J. Polym. Eng. 2021, 41, 768–787. [Google Scholar] [CrossRef]
- Ma, H.; Gao, B.; Wang, M.; Yuan, Z.; Shen, J.; Zhao, J.; Feng, Y. Strategies for enhancing thermal conductivity of polymer-based thermal interface materials: A review. J. Mater. Sci. 2020, 56, 1064–1086. [Google Scholar] [CrossRef]
- Chen, H.; Ginzburg, V.V.; Yang, J.; Yang, Y.; Liu, W.; Huang, Y.; Du, L.; Chen, B. Thermal conductivity of polymer-based composites: Fundamentals and applications. Prog. Polym. Sci. 2016, 59, 41–85. [Google Scholar] [CrossRef]
- Sun, J.; Zhuang, J.; Jiang, H.; Huang, Y.; Zheng, X.; Liu, Y.; Wu, D. Thermal dissipation performance of metal-polymer composite heat exchanger with V-shape microgrooves: A numerical and experimental study. Appl. Therm. Eng. 2017, 121, 492–500. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Sun, B.; Jiang, P. Highly Thermally Conductive Yet Electrically Insulating Polymer/Boron Nitride Nanosheets Nanocomposite Films for Improved Thermal Management Capability. ACS Nano 2018, 13, 337–345. [Google Scholar] [CrossRef]
- Ding, D.; Zou, M.; Wang, X.; Qin, G.; Zhang, S.; Chan, S.Y.; Meng, Q.; Liu, Z.; Zhang, Q.; Chen, Y. Thermal conductivity of polydisperse hexagonal BN/polyimide composites: Iterative EMT model and machine learning based on first principles investigation. Chem. Eng. J. 2022, 437, 135438. [Google Scholar] [CrossRef]
- Haruki, M.; Tada, J.; Tanaka, K.; Onishi, H.; Tada, Y. Enhancing the effective thermal conductivity of Kapton-type polyimide sheets via the use of hexagonal boron nitride. Thermochim. Acta 2018, 662, 1–7. [Google Scholar] [CrossRef]
- Li, T.-L.; Hsu, S.L.-C. Enhanced Thermal Conductivity of Polyimide Films via a Hybrid of Micro- and Nano-Sized Boron Nitride. J. Phys. Chem. B 2010, 114, 6825–6829. [Google Scholar] [CrossRef]
- Song, Q.; Zhu, W.; Deng, Y.; Hai, F.; Wang, Y.; Guo, Z. Enhanced through-plane thermal conductivity and high electrical insulation of flexible composite films with aligned boron nitride for thermal interface material. Compos. Part A Appl. Sci. Manuf. 2019, 127, 105654. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Wang, X. Thermal conductivity enhancement of polymers via structure tailoring. J. Enhanc. Heat Transf. 2020, 27, 463–489. [Google Scholar] [CrossRef]
- Yoon, D.; Lee, H.; Kim, T.; Song, Y.; Lee, T.; Lee, J.; Seol, J.H. Enhancing the thermal conductivity of amorphous polyimide by molecular-scale manipulation. Eur. Polym. J. 2023, 184, 111775. [Google Scholar] [CrossRef]
- Singh, V.; Bougher, T.L.; Weathers, A.; Cai, Y.; Bi, K.; Pettes, M.; McMenamin, S.A.; Lv, W.; Resler, D.P.; Gattuso, T.R.; et al. High thermal conductivity of chain-oriented amorphous polythiophene. Nat. Nanotechnol. 2014, 9, 384–390. [Google Scholar] [CrossRef] [PubMed]
- Novichenok, L.N.; Ovchinnikova, S.M. Thermal conductivity of certain oriented polymers. J. Eng. Phys. Thermophys. 1982, 42, 648–651. [Google Scholar] [CrossRef]
- Dong, L.; Xi, Q.; Chen, D.; Guo, J.; Nakayama, T.; Li, Y.; Liang, Z.; Zhou, J.; Xu, X.; Li, B. Dimensional crossover of heat conduction in amorphous polyimide nanofibers. Natl. Sci. Rev. 2018, 5, 500–506. [Google Scholar] [CrossRef] [Green Version]
- Nazarychev, V.M.; Glova, A.D.; Larin, S.V.; Lyulin, A.V.; Lyulin, S.V.; Gurtovenko, A.A. Cooling-Rate Computer Simulations for the Description of Crystallization of Organic Phase-Change Materials. Int. J. Mol. Sci. 2022, 23, 14576. [Google Scholar] [CrossRef]
- Abdi, A.; Ignatowicz, M.; Gunasekara, S.N.; Chiu, J.N.; Martin, V. Experimental investigation of thermo-physical properties of n-octadecane and n-eicosane. Int. J. Heat Mass Transf. 2020, 161, 120285. [Google Scholar] [CrossRef]
- Vélez, C.; Khayet, M.; de Zárate, J.O. Temperature-dependent thermal properties of solid/liquid phase change even-numbered n-alkanes: N-Hexadecane, n-octadecane and n-eicosane. Appl. Energy 2015, 143, 383–394. [Google Scholar] [CrossRef]
- Minnich, A.J. Exploring the Extremes of Heat Conduction in Anisotropic Materials. Nanoscale Microscale Thermophys. Eng. 2016, 20, 1–21. [Google Scholar] [CrossRef]
- Lu, T.; Kim, K.; Li, X.; Zhou, J.; Chen, G.; Liu, J. Thermal transport in semicrystalline polyethylene by molecular dynamics simulation. J. Appl. Phys. 2018, 123, 6889. [Google Scholar] [CrossRef] [Green Version]
- Ruan, K.; Guo, Y.; Gu, J. Liquid Crystalline Polyimide Films with High Intrinsic Thermal Conductivities and Robust Toughness. Macromolecules 2021, 54, 4934–4944. [Google Scholar] [CrossRef]
- Kurabayashi, K.; Asheghi, M.; Touzelbaev, M.; Goodson, K. Measurement of the thermal conductivity anisotropy in polyimide films. J. Microelectromechanical Syst. 1999, 8, 180–191. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Yang, R. Tuning the thermal conductivity of polymers with mechanical strains. Phys. Rev. B 2010, 81, 1–9. [Google Scholar] [CrossRef]
- Prajapati, H.; Chalise, D.; Ravoori, D.; Taylor, R.M.; Jain, A. Improvement in build-direction thermal conductivity in extrusion-based polymer additive manufacturing through thermal annealing. Addit. Manuf. 2019, 26, 242–249. [Google Scholar] [CrossRef]
- Lin, D.; Jiang, M.; Li, R.; Qi, S.; Wu, D. Clarifying the Effect of Drafting Conditions on Structure and Properties of Polyimide Fibers at Molecular Dynamic Level. Macromol. Theory Simul. 2022, 31, 2100081. [Google Scholar] [CrossRef]
- Lin, D.; Jiang, M.; Qi, S.; Wu, D. Macromolecular structural evolution of polyimide chains during large-ratio uniaxial fiber orientation process revealed by molecular dynamics simulation. Chem. Phys. Lett. 2020, 756, 137847. [Google Scholar] [CrossRef]
- Xiang, L.; Fang, Y.; Xu, K.; Zheng, Z.; Dong, J.; Xie, Y. Molecular alignment induced high thermal conductivity in amorphous/ low crystalline polyimide fibers. Int. J. Heat Mass Transf. 2022, 193, 122959. [Google Scholar] [CrossRef]
- Shen, S.; Henry, A.; Tong, J.; Zheng, R.; Chen, G. Polyethylene nanofibres with very high thermal conductivities. Nat. Nanotechnol. 2010, 5, 251–255. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, J.; Wang, T.; Han, M.; Valloppilly, S.; Xu, S.; Wang, X. Novel Polyethylene Fibers of Very High Thermal Conductivity Enabled by Amorphous Restructuring. ACS Omega 2017, 2, 3931–3944. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Kim, K.; Wang, Y.; Liu, J. Strain effects on the anisotropic thermal transport in crystalline polyethylene. Appl. Phys. Lett. 2018, 112, 986. [Google Scholar] [CrossRef]
- Muthaiah, R.; Garg, J. Temperature effects in the thermal conductivity of aligned amorphous polyethylene—A molecular dynamics study. J. Appl. Phys. 2018, 124, 105102. [Google Scholar] [CrossRef] [Green Version]
- Simavilla, D.N.; Sgouros, A.P.; Vogiatzis, G.G.; Tzoumanekas, C.; Georgilas, V.; Verbeeten, W.M.; Theodorou, D.N. Molecular Dynamics Test of the Stress-Thermal Rule in Polyethylene and Polystyrene Entangled Melts. Macromolecules 2020, 53, 789–802. [Google Scholar] [CrossRef]
- Donovan, B.F.; Warzoha, R.J.; Cosby, T.; Giri, A.; Wilson, A.A.; Borgdorff, A.J.; Vu, N.T.; Patterson, E.A.; Gorzkowski, E.P. Strained Polymer Thermal Conductivity Enhancement Counteracted by Additional Off-Axis Strain. Macromolecules 2020, 53, 11089–11097. [Google Scholar] [CrossRef]
- Ito, T.; Matsubara, H.; Surblys, D.; Ohara, T. Molecular dynamics study on the thermal conductivity of a single polyethylene chain: Strain dependence and potential models’ effect. AIP Adv. 2022, 12, 105223. [Google Scholar] [CrossRef]
- Hennig, J.; Knappe, W. Anisotropy of thermal conductivity in stretched amorphous linear polymers and in strained elastomers. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 167–174. [Google Scholar] [CrossRef]
- Wu, T.; Zhu, J.; Yu, H.; Qu, S.; Yang, W. Stretch induced thermal conduction anisotropy of hydrogel. Int. J. Heat Mass Transf. 2022, 185, 122445. [Google Scholar] [CrossRef]
- Lyulin, S.V.; Larin, S.V.; Gurtovenko, A.A.; Nazarychev, V.M.; Falkovich, S.G.; Yudin, V.E.; Svetlichnyi, V.M.; Gofman, I.V.; Lyulin, A.V. Thermal properties of bulk polyimides: Insights from computer modeling versus experiment. Soft Matter 2013, 10, 1224–1232. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Dobrovskiy, A.Y.; Larin, S.; Lyulin, A.; Lyulin, S. Simulating local mobility and mechanical properties of thermostable polyimides with different dianhydride fragments. J. Polym. Sci. Part B Polym. Phys. 2017, 56, 375–382. [Google Scholar] [CrossRef]
- Hegde, M.; Lafont, U.; Norder, B.; Samulski, E.T.; Rubinstein, M.; Dingemans, T.J. SWCNT induced crystallization in amorphous and semi-crystalline poly(etherimide)s: Morphology and thermo-mechanical properties. Polymer 2014, 55, 3746–3757. [Google Scholar] [CrossRef]
- Yudin, V.; Feldman, A.; Svetlichnyi, V.; Shumakov, A.; Marom, G. Crystallization of R-BAPB type polyimide modified by carbon nano-particles. Compos. Sci. Technol. 2007, 67, 789–794. [Google Scholar] [CrossRef]
- Ivan’Kova, E.; Kasatkin, I.; Popova, E.; Didenko, A.; Yudin, V. WAXS in-situ study of R-BAPB polyetherimid double-melting behavior. Polym. Test. 2022, 108, 107522. [Google Scholar] [CrossRef]
- Sabic Innovative Plastics ULTEMTM 1000 RESIN. Available online: https://www.sabic.com/en/products/specialties/ultem-resin-family-of-high-heat-solutions/ultem-resin (accessed on 28 June 2023).
- Larin, S.V.; Falkovich, S.G.; Nazarychev, V.M.; Gurtovenko, A.A.; Lyulin, A.V.; Lyulin, S.V. Molecular-dynamics simulation of polyimide matrix pre-crystallization near the surface of a single-walled carbon nanotube. RSC Adv. 2013, 4, 830–844. [Google Scholar] [CrossRef]
- Dobrovskiy, A.Y.; Nazarychev, V.M.; Volgin, I.V.; Lyulin, S.V. The Transport Properties of Semi-Crystalline Polyetherimide BPDA-P3 in Amorphous and Ordered States: Computer Simulations. Membranes 2022, 12, 856. [Google Scholar] [CrossRef]
- Fal’kovich, S.G.; Larin, S.; Nazarychev, V.; Volgin, I.; Gurtovenko, A.; Lyulin, S. Computer simulation of the heat-resistant polyimides ULTEM™ and EXTEM™ with the use of GROMOS53a6 and AMBER99 force fields. Polym. Sci. Ser. A 2014, 56, 558–567. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Vaganov, G.V.; Larin, S.V.; Didenko, A.L.; Elokhovskiy, V.Y.; Svetlichnyi, V.M.; Yudin, V.E.; Lyulin, S.V. Rheological and Mechanical Properties of Thermoplastic Crystallizable Polyimide-Based Nanocomposites Filled with Carbon Nanotubes: Computer Simulations and Experiments. Polymers 2022, 14, 3154. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef]
- Larin, S.V.; Nazarychev, V.M.; Dobrovskiy, A.Y.; Lyulin, A.V.; Lyulin, S.V. Structural Ordering in SWCNT-Polyimide Nanocomposites and Its Influence on Their Mechanical Properties. Polymers 2018, 10, 1245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falkovich, S.G.; Nazarychev, V.M.; Larin, S.V.; Kenny, J.M.; Lyulin, S.V. Mechanical Properties of a Polymer at the Interface Structurally Ordered by Graphene. J. Phys. Chem. C 2016, 120, 6771–6777. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Glova, A.D.; Volgin, I.V.; Larin, S.V.; Lyulin, A.V.; Lyulin, S.V.; Gurtovenko, A.A. Evaluation of thermal conductivity of organic phase-change materials from equilibrium and non-equilibrium computer simulations: Paraffin as a test case. Int. J. Heat Mass Transf. 2020, 165, 120639. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Boomstra, M.; van Asseldonk, M.; Geurts, B.; Nazarychev, V.; Lyulin, A. Effects of branching and polydispersity on thermal conductivity of paraffin waxes. Int. J. Heat Mass Transf. 2022, 195, 123192. [Google Scholar] [CrossRef]
- Nagoya, A.; Kikkawa, N.; Ohba, N.; Baba, T.; Kajita, S.; Yanai, K.; Takeno, T. Autonomous Search for Polymers with High Thermal Conductivity Using a Rapid Green–Kubo Estimation. Macromolecules 2022, 55, 3384–3395. [Google Scholar] [CrossRef]
- Ouinten, M.-L.; Szymczyk, A.; Ghoufi, A. Molecular Dynamics Simulation Study of Organic Solvents Confined in PIM-1 and P84 Polyimide Membranes. J. Phys. Chem. B 2023, 127, 1237–1243. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Jiménez-Osés, G.; Liu, P.; Fang, Y.; Zhang, J.; Lai, Y.-C.; Park, S.; Chen, L.; Houk, K.N.; et al. N-Type Conjugated Polymer-Enabled Selective Dispersion of Semiconducting Carbon Nanotubes for Flexible CMOS-Like Circuits. Adv. Funct. Mater. 2015, 25, 1837–1844. [Google Scholar] [CrossRef]
- Riniker, S. Fixed-Charge Atomistic Force Fields for Molecular Dynamics Simulations in the Condensed Phase: An Overview. J. Chem. Inf. Model. 2018, 58, 565–578. [Google Scholar] [CrossRef]
- da Silva, A.W.S.; Vranken, W.F. ACPYPE—AnteChamber PYthon Parser interfacE. BMC Res. Notes 2012, 5, 367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Ben-Shalom, I.Y.; Berryman, J.T.; Brozell, S.R.; Cerutti, D.S.; Cheatham, I.T.E.; Cisneros, G.A.; Cruzeiro, V.W.D.; et al. Amber 2022; University of California: San Francisco, CA, USA. [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 09 (Revision D.2); Gaussian, Inc.: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Lyulin, S.; Gurtovenko, A.; Larin, S.; Nazarychev, V. Microsecond Atomic-Scale Molecular Dynamics Simulations of Polyimides. Macromolecules 2013, 46, 6357–6363. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2007, 4, 116–122. [Google Scholar] [CrossRef] [PubMed]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Larin, S.V.; Lyulin, A.V.; Dingemans, T.; Kenny, J.M.; Lyulin, S.V. Atomistic Molecular Dynamics Simulations of the Initial Crystallization Stage in an SWCNT-Polyetherimide Nanocomposite. Polymers 2017, 9, 548. [Google Scholar] [CrossRef] [Green Version]
- Ming, Y.; Zhou, Z.; Hao, T.; Nie, Y. Molecular simulation of polymer crystallization under chain and space confinement. Phys. Chem. Chem. Phys. 2021, 23, 17382–17391. [Google Scholar] [CrossRef] [PubMed]
- Yudin, V.E.; Svetlichnyi, V.M.; Shumakov, A.N.; Letenko, D.G.; Feldman, A.Y.; Marom, G. The Nucleating Effect of Carbon Nanotubes on Crystallinity in R-BAPB-Type Thermoplastic Polyimide. Macromol. Rapid Commun. 2005, 26, 885–888. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Lyulin, A.V.; Larin, S.V.; Gurtovenko, A.A.; Kenny, J.M.; Lyulin, S.V. Molecular dynamics simulations of uniaxial deformation of thermoplastic polyimides. Soft Matter 2016, 12, 3972–3981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dingemans, T.J.; Mendes, E.; Hinkley, J.J.; Weiser, E.S.; StClair, T.L. Poly(ether imide)s from Diamines with Para-, Meta-, and Ortho-Arylene Substitutions: Synthesis, Characterization, and Liquid Crystalline Properties. Macromolecules 2008, 41, 2474–2483. [Google Scholar] [CrossRef]
- Zhang, T.; Luo, T. Role of Chain Morphology and Stiffness in Thermal Conductivity of Amorphous Polymers. J. Phys. Chem. B 2016, 120, 803–812. [Google Scholar] [CrossRef]
- Lin, C.; Rao, Z. Thermal conductivity enhancement of paraffin by adding boron nitride nanostructures: A molecular dynamics study. Appl. Therm. Eng. 2017, 110, 1411–1419. [Google Scholar] [CrossRef]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 2002, 65, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Surblys, D.; Matsubara, H.; Kikugawa, G.; Ohara, T. Application of atomic stress to compute heat flux via molecular dynamics for systems with many-body interactions. Phys. Rev. E 2019, 99, 051301. [Google Scholar] [CrossRef] [Green Version]
- Boone, P.; Babaei, H.; Wilmer, C.E. Heat Flux for Many-Body Interactions: Corrections to LAMMPS. J. Chem. Theory Comput. 2019, 15, 5579–5587. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Lussetti, E.; de Souza, L.E.S.; Müller-Plathe, F. Thermal Conductivities of Molecular Liquids by Reverse Nonequilibrium Molecular Dynamics. J. Phys. Chem. B 2005, 109, 15060–15067. [Google Scholar] [CrossRef] [PubMed]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]
- Babaei, H.; Keblinski, P.; Khodadadi, J. Improvement in thermal conductivity of paraffin by adding high aspect-ratio carbon-based nano-fillers. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2013, 377, 1358–1361. [Google Scholar] [CrossRef]
- Bagri, A.; Kim, S.-P.; Ruoff, R.S.; Shenoy, V.B. Thermal transport across Twin Grain Boundaries in Polycrystalline Graphene from Nonequilibrium Molecular Dynamics Simulations. Nano Lett. 2011, 11, 3917–3921. [Google Scholar] [CrossRef] [PubMed]
- Volgin, I.V.; Batyr, P.A.; Matseevich, A.V.; Dobrovskiy, A.Y.; Andreeva, M.V.; Nazarychev, V.M.; Larin, S.V.; Goikhman, M.Y.; Vizilter, Y.V.; Askadskii, A.A.; et al. Machine Learning with Enormous “Synthetic” Data Sets: Predicting Glass Transition Temperature of Polyimides Using Graph Convolutional Neural Networks. ACS Omega 2022, 7, 43678–43691. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Larin, S.V.; Yakimansky, A.V.; Lukasheva, N.V.; Gurtovenko, A.A.; Gofman, I.V.; Yudin, V.E.; Svetlichnyi, V.M.; Kenny, J.M.; Lyulin, S.V. Parameterization of electrostatic interactions for molecular dynamics simulations of heterocyclic polymers. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 912–923. [Google Scholar] [CrossRef]
- Falkovich, S.G.; Lyulin, S.V.; Nazarychev, V.M.; Larin, S.V.; Gurtovenko, A.A.; Lukasheva, N.V.; Lyulin, A.V. Influence of the electrostatic interactions on thermophysical properties of polyimides: Molecular-dynamics simulations. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 640–646. [Google Scholar] [CrossRef] [Green Version]
- Dashora, P.; Gupta, G. On the temperature dependence of the thermal conductivity of linear amorphous polymers. Polymer 1996, 37, 231–234. [Google Scholar] [CrossRef]
- Fischer, C.; Drummer, D. Crystallization and Mechanical Properties of Polypropylene under Processing-Relevant Cooling Conditions with respect to Isothermal Holding Time. Int. J. Polym. Sci. 2016, 2016, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Park, S.H.; Lee, S.G.; Kim, S.H. Isothermal crystallization behavior and mechanical properties of polylactide/carbon nanotube nanocomposites. Compos. Part A Appl. Sci. Manuf. 2013, 46, 11–18. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Q.; Wang, G.; Liu, S. The effect of isothermal crystallization on mechanical properties of poly(ethylene 2,5-furandicarboxylate). e-Polymers 2021, 22, 1–11. [Google Scholar] [CrossRef]
- Sæther, S.; Falck, M.; Zhang, Z.; Lervik, A.; He, J. Thermal Transport in Polyethylene: The Effect of Force Fields and Crystallinity. Macromolecules 2021, 54, 6563–6574. [Google Scholar] [CrossRef]








| Partial Charge Calculation Method | AM1-BCC | HF/6-31G* (RESP) | ||
|---|---|---|---|---|
| Thermal conductivity calculation methods | EMD | NEMD | EMD | NEMD |
| Thermal conductivity of ULTEMTM, T = 290 K | 0.284 ± 0.005 | 0.296 ± 0.001 | 0.265 ± 0.001 | 0.339 ± 0.001 |
| 29.1% | 34.5% | 20.5% | 54.1% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazarychev, V.M.; Lyulin, S.V. The Effect of Mechanical Elongation on the Thermal Conductivity of Amorphous and Semicrystalline Thermoplastic Polyimides: Atomistic Simulations. Polymers 2023, 15, 2926. https://doi.org/10.3390/polym15132926
Nazarychev VM, Lyulin SV. The Effect of Mechanical Elongation on the Thermal Conductivity of Amorphous and Semicrystalline Thermoplastic Polyimides: Atomistic Simulations. Polymers. 2023; 15(13):2926. https://doi.org/10.3390/polym15132926
Chicago/Turabian StyleNazarychev, Victor M., and Sergey V. Lyulin. 2023. "The Effect of Mechanical Elongation on the Thermal Conductivity of Amorphous and Semicrystalline Thermoplastic Polyimides: Atomistic Simulations" Polymers 15, no. 13: 2926. https://doi.org/10.3390/polym15132926
APA StyleNazarychev, V. M., & Lyulin, S. V. (2023). The Effect of Mechanical Elongation on the Thermal Conductivity of Amorphous and Semicrystalline Thermoplastic Polyimides: Atomistic Simulations. Polymers, 15(13), 2926. https://doi.org/10.3390/polym15132926