Self-Assembly of Symmetric Copolymers in Slits with Inert and Attractive Walls
Abstract
:1. Introduction
2. Methodology
2.1. Simulation Method
2.2. Simulation Details
3. Results and Discussion
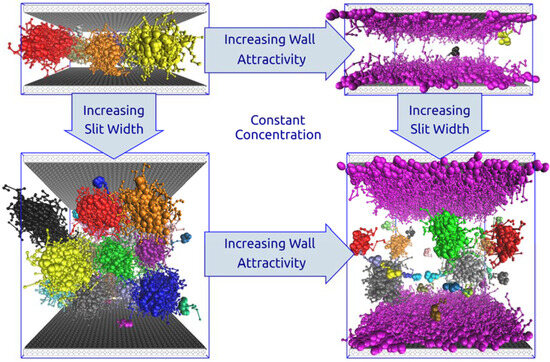
3.1. Unconfined Semi-Dilute Solutions
3.2. Sterically Confined Self-Assembling Systems in Slits
3.3. Self-Assembly in Slits with Inert and Slightly Repulsive Walls
3.4. Slightly Attractive Walls
3.5. Strongly Attractive Walls
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DPD | Dissipative particle dynamics |
| EICA | Evaporation-induced confinement assembly |
| FENE | Finitely extendible non-linear elastic |
| FH | Flory–Huggins |
References
- Nagarajan, R. Constructing a molecular theory of self-assembly: Interplay of ideas from surfactants and block copolymers. Adv. Colloid Interface Sci. 2017, 244, 113–123. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, R.; Ganesh, K. Block copolymer self-assembly in selective solvents–spherical micelles with segregated cores. J. Chem. Phys. 1989, 90, 5843–5856. [Google Scholar] [CrossRef]
- Syamala, P.P.N.; Wurthner, F. Modulation of the Self-Assembly of pi-Amphiphiles in Water from Enthalpy- to Entropy-Driven by Enwrapping Substituents. Chem. A Eur. J. 2020, 26, 8426–8434. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Yu, L.L.; Dong, H.Z.; Zhu, J.M.; Yang, L.; Yuan, X.S. Photo-Responsive Micelles with Controllable and Co-Release of Carbon Monoxide, Formaldehyde and Doxorubicin. Polymers 2022, 14, 2416. [Google Scholar] [CrossRef]
- Avsar, S.Y.; Kyropoulou, M.; Di Leone, S.; Schoenenberger, C.A.; Meier, W.P.; Palivan, C.G. Biomolecules Turn Self-Assembling Amphiphilic Block Co-polymer Platforms Into Biomimetic Interfaces. Front. Chem. 2019, 6, 645. [Google Scholar] [CrossRef]
- Kataoka, K.; Harada, A.; Nagasaki, Y. Block copolymer micelles for drug delivery: Design, characterization and biological significance. Adv. Drug Deliv. Rev. 2012, 64, 37–48. [Google Scholar] [CrossRef]
- Blanazs, A.; Armes, S.P.; Ryan, A.J. Self-Assembled Block Copolymer Aggregates: From Micelles to Vesicles and their Biological Applications. Macromol. Rapid Commun. 2009, 30, 267–277. [Google Scholar] [CrossRef]
- Kabanov, A.V.; Alakhov, V.Y. Pluronic (R) block copolymers in drug delivery: From micellar nanocontainers to biological response modifiers. Crit. Rev. Ther. Drug Carr. Syst. 2002, 19, 1–72. [Google Scholar] [CrossRef] [PubMed]
- Chrysostomou, V.; Forys, A.; Trzebicka, B.; Demetzos, C.; Pispas, S. Amphiphilic Copolymer-Lipid Chimeric Nanosystems as DNA Vectors. Polymers 2022, 14, 4901. [Google Scholar] [CrossRef]
- Huang, C.W.; Chang, Y.Y.; Cheng, C.C.; Hung, M.T.; Mohamed, M.G. Self-Assembled Supramolecular Micelles Based on Multiple Hydrogen Bonding Motifs for the Encapsulation and Release of Fullerene. Polymers 2022, 14, 4923. [Google Scholar] [CrossRef]
- Perumal, S.; Atchudan, R.; Lee, W. A Review of Polymeric Micelles and Their Applications. Polymers 2022, 14, 2510. [Google Scholar] [CrossRef] [PubMed]
- Hils, C.; Manners, I.; Schöbel, J.; Schmalz, H. Patchy Micelles with a Crystalline Core: Self-Assembly Concepts, Properties, and Applications. Polymers 2021, 13, 1481. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.L.; Zhou, X.; Yue, K.; Guo, Z.H. Synthesis and Self-Assembly of Conjugated Block Copolymers. Polymers 2021, 13, 110. [Google Scholar] [CrossRef] [PubMed]
- Gohy, J.-F.; Zhao, Y. Photo-responsive block copolymer micelles: Design and behavior. Chem. Soc. Rev. 2013, 42, 7117–7129. [Google Scholar] [CrossRef] [PubMed]
- Walther, A.; Mueller, A.H.E. Janus Particles: Synthesis, Self-Assembly, Physical Properties, and Applications. Chem. Rev. 2013, 113, 5194–5261. [Google Scholar] [CrossRef] [PubMed]
- Mai, Y.Y.; Eisenberg, A. Self-assembly of block copolymers. Chem. Soc. Rev. 2012, 41, 5969–5985. [Google Scholar] [CrossRef]
- Moughton, A.O.; Hillmyer, M.A.; Lodge, T.P. Multicompartment Block Polymer Micelles. Macromolecules 2012, 45, 2–19. [Google Scholar] [CrossRef]
- O’Reilly, R.K.; Hawker, C.J.; Wooley, K.L. Cross-linked block copolymer micelles: Functional nanostructures of great potential and versatility. Chem. Soc. Rev. 2006, 35, 1068–1083. [Google Scholar] [CrossRef]
- Uchman, M.; Stepanek, M.; Prevost, S.; Angelov, B.; Bednar, J.; Appavou, M.S.; Gradzielski, M.; Prochazka, K. Coassembly of Poly(ethylene oxide)-block-poly(methacrylic acid) and N-Dodecylpyridinium Chloride in Aqueous Solutions Leading to Ordered Micellar Assemblies within Copolymer Aggregates. Macromolecules 2012, 45, 6471–6480. [Google Scholar] [CrossRef]
- Podhajecka, K.; Stepanek, M.; Prochazka, K.; Brown, W. Hybrid polymeric micelles with hydrophobic cores and mixed polyelectrolyte/nonelectrolyte shells in aqueous media. 2. Studies of the shell behavior. Langmuir 2001, 17, 4245–4250. [Google Scholar] [CrossRef]
- Matejicek, P.; Uhlik, F.; Limpouchova, Z.; Prochazka, K.; Tuzar, Z.; Webber, S. Experimental study of hydrophobically modified amphiphilic block copolymer micelles using light scattering and nonradiative excitation energy transfer. Macromolecules 2002, 35, 9487–9496. [Google Scholar] [CrossRef]
- Plestil, J.; Kriz, J.; Tuzar, Z.; Prochazka, K.; Melnichenko, Y.B.; Wignall, G.D.; Talingting, M.R.; Munk, P.; Webber, S.E. Small-angle neutron scattering study of onion-type micelles. Macromol. Chem. Phys. 2001, 202, 553–563. [Google Scholar] [CrossRef]
- Wong, C.K.; Qiang, X.; Müller, A.H.; Gröschel, A.H. Self-Assembly of block copolymers into internally ordered microparticles. Prog. Polym. Sci. 2020, 102, 101211. [Google Scholar] [CrossRef]
- Ok, S.; Vayer, M.; Sinturel, C. A decade of innovation and progress in understanding the morphology and structure of heterogeneous polymers in rigid confinement. Soft Matter 2021, 17, 7430–7458. [Google Scholar] [CrossRef]
- Tong, L.; Nabae, Y.; Hirai, T.; Yabu, H.; Hayakawa, T. Creation of Thermal Response Ordered Mesostructure Polymer Particles Using Diblock Copolymers via 3D Confined Self-Assembly. Macromol. Chem. Phys. 2023, 224, 2200402. [Google Scholar] [CrossRef]
- Juan, Y.T.; Lai, Y.F.; Li, X.Y.; Tai, T.C.; Huang, C.F.; Lin, C.H.; Li, B.H.; Shi, A.C.; Hsueh, H.Y. Self-Assembly of Gyroid-Forming Diblock Copolymers under Spherical Confinement. Macromolecules 2023, 56, 457–469. [Google Scholar] [CrossRef]
- Ashwini, T.; Narayan, R.; Shenoy, P.A.; Nayak, U.Y. Computational modeling for the design and development of nano based drug delivery systems. J. Mol. Liq. 2022, 368, 120596. [Google Scholar] [CrossRef]
- Peng, M.L.; Hu, D.W.; Chang, X.H.; Zhu, Y.T. Confined Self-Assembly of Block Copolymers within Emulsion Droplets: A Perspective. J. Phys. Chem. B 2022, 126, 9435–9442. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, G.; Liu, F. Block copolymer microspheres containing intricate nanometer-sized segregation patterns. Macromolecules 2001, 34, 8814–8817. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, K.; Tan, H.; Xu, J.; Zhu, J. Emulsion solvent evaporation-induced self-assembly of block copolymers containing pH-sensitive block. Langmuir 2017, 33, 9889–9896. [Google Scholar] [CrossRef]
- Ku, K.H.; Shin, J.M.; Klinger, D.; Jang, S.G.; Hayward, R.C.; Hawker, C.J.; Kim, B.J. Particles with tunable porosity and morphology by controlling interfacial instability in block copolymer emulsions. ACS Nano 2016, 10, 5243–5251. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Limpouchova, Z.; Prochazka, K.; Raya, R.K.; Min, Y.G. Modeling the Phase Equilibria of Associating Polymers in Porous Media with Respect to Chromatographic Applications. Polymers 2022, 14, 3182. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.L.; Ke, F.F.; Li, Y.C.; Shi, Y.; Zhang, Z.; Chen, Y.M. Emulsion confined block copolymer self-assembly: Recent progress and prospect. Nano Res. 2023, 16, 564–582. [Google Scholar] [CrossRef]
- Mendoza, C.; Nirwan, V.P.; Fahmi, A. Nanofabrication of hybrid nanomaterials: Macroscopically aligned nanoparticles pattern via directed self-assembly of block copolymers. J. Appl. Polym. Sci. 2023, 140, e53409. [Google Scholar] [CrossRef]
- Cifra, P.; Bleha, T. Piston Compression of Semiflexible Ring Polymers in Channels. Macromol. Theory Simul. 2021, 30, 2100027. [Google Scholar] [CrossRef]
- Mijangos, C.; Hernandez, R.; Martin, J. A review on the progress of polymer nanostructures with modulated morphologies and properties, using nanoporous AAO templates. Prog. Polym. Sci. 2016, 54–55, 148–182. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci. Part B-Polym. Phys. 2012, 50, 1515–1555. [Google Scholar] [CrossRef]
- Binder, K.; Kreer, T.; Milchev, A. Polymer brushes under flow and in other out-of-equilibrium conditions. Soft Matter 2011, 7, 7159–7172. [Google Scholar] [CrossRef]
- Viduna, D.; Limpouchova, Z.; Prochazka, K. Monte Carlo simulation of polymer brushes in narrow pores. J. Chem. Phys. 2001, 115, 7309–7318. [Google Scholar] [CrossRef]
- Limpouchova, Z.; Viduna, D.; Prochazka, K. Mixed systems of tethered chains in spherical volumes. A model for cores of mixed copolymer micelles. Macromolecules 1997, 30, 8027–8035. [Google Scholar] [CrossRef]
- Wang, X.; Procházka, K.; Limpouchová, Z. Partitioning of polymers between bulk and porous media: Monte Carlo study of the effect of pore size distribution. J. Colloid Interface Sci. 2020, 567, 103–112. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Prochazka, K.; Limpouchova, Z. Pore size effect on the separation of polymers by interaction chromatography. A Monte Carlo study. Anal. Chim. Acta 2019, 1064, 126–137. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Limpouchova, Z.; Prochazka, K. Separation of polymers differing in their chain architecture by interaction chromatography: Phase equilibria and conformational behavior of polymers in strongly adsorbing porous media. Polymer 2019, 175, 99–106. [Google Scholar] [CrossRef]
- Ahn, J.; Chang, T.; Wang, X.; Limpouchova, Z.; Prochazka, K. Influence of the chain architecture and the presence of end-groups or branching units chemically different from repeating structural units on the critical adsorption point in liquid chromatography. Macromolecules 2017, 50, 8720–8730. [Google Scholar] [CrossRef]
- Cifra, P.; Bleha, T. Confined macromolecules in polymer materials and processes. New Polym. Mater. 2005, 916, 238–251. [Google Scholar]
- Skrinarova, Z.; Bleha, T.; Cifra, P. Concentration effects in partitioning of macromolecules into pores with attractive walls. Macromolecules 2002, 35, 8896–8905. [Google Scholar] [CrossRef]
- Hou, C.L.; Gao, L.J.; Wang, Y.M.; Yan, L.T. Entropic control of nanoparticle self-assembly through confinement. Nanoscale Horiz. 2022, 7, 1016–1028. [Google Scholar] [CrossRef]
- Huang, J.-H.; Wu, J.-J.; Huang, X.-W. Self-assembly of symmetric rod-coil diblock copolymers in cylindrical nanopore. RSC Adv. 2016, 6, 100559–100567. [Google Scholar] [CrossRef]
- Deng, R.H.; Li, H.; Liang, F.X.; Zhu, J.T.; Li, B.H.; Xie, X.L.; Yang, Z.Z. Soft Colloidal Molecules with Tunable Geometry by 3D Confined Assembly of Block Copolymers. Macromolecules 2015, 48, 5855–5860. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Espanol, P.; Warren, P.B. Perspective: Dissipative particle dynamics. J. Chem. Phys. 2017, 146, 150901. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Melchor, M.; Mayoral, E.; Velazquez, M.E.; Alejandre, J. Electrostatic interactions in dissipative particle dynamics using the Ewald sums. J. Chem. Phys. 2006, 125, 224107. [Google Scholar] [CrossRef] [PubMed]
- Groot, R.D. Applications of dissipative particle dynamics. In Novel Methods in Soft Matter Simulations; Karttunen, M., Vattulainen, I., Lukkarinen, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 5–38. [Google Scholar]
- Groot, R.D. Electrostatic interactions in dissipative particle dynamics–simulation of polyelectrolytes and anionic surfactants (vol 118, pg 11265, 2003). J. Chem. Phys. 2003, 119, 10454. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Espanol, P.; Warren, P. Statistical-mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Zhao, J.Y.; Chen, S.; Zhang, K.X.; Liu, Y. A review of many-body dissipative particle dynamics (MDPD): Theoretical models and its applications. Phys. Fluids 2021, 33, 112002. [Google Scholar] [CrossRef]
- Lombardo, D.; Kiselev, M.A.; Magazù, S.; Calandra, P. Amphiphiles Self-Assembly: Basic Concepts and Future Perspectives of Supramolecular Approaches. Adv. Condens. Matter Phys. 2015, 2015, 151683. [Google Scholar] [CrossRef]
- Blovský, T.; Šindelka, K.; Limpouchová, Z.; Procházka, K. Changes in Ion Concentrations upon the Binding of Short Polyelectrolytes on Phospholipid Bilayers: Computer Study Addressing Interesting Physiological Consequences. Polymers 2022, 14, 3634. [Google Scholar] [CrossRef]
- Prochazka, K.; Limpouchova, Z.; Stepanek, M.; Sindelka, K.; Lisal, M. DPD Modelling of the Self- and Co-Assembly of Polymers and Polyelectrolytes in Aqueous Media: Impact on Polymer Science. Polymers 2022, 14, 404. [Google Scholar] [CrossRef]
- Sindelka, K.; Limpouchova, Z.; Prochazka, K. Solubilization of Charged Porphyrins in Interpolyelectrolyte Complexes: A Computer Study. Polymers 2021, 13, 502. [Google Scholar] [CrossRef]
- Sindelka, K.; Limpouchova, Z.; Lisal, M.; Prochazka, K. The electrostatic co-assembly in non-stoichiometric aqueous mixtures of copolymers composed of one neutral water-soluble and one polyelectrolyte (either positively or negatively charged) block: A dissipative particle dynamics study. Phys. Chem. Chem. Phys. 2016, 18, 16137–16151. [Google Scholar] [CrossRef]
- Groot, R.D.; Rabone, K.L. Mesoscopic simulation of cell membrane damage, morphology change and rupture by nonionic surfactants. Biophys. J. 2001, 81, 725–736. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University: New York, NY, USA, 2003; p. 440. [Google Scholar]
- Sindelka, K.; Lisal, M. Interplay between surfactant self-assembly and adsorption at hydrophobic surfaces: Insights from dissipative particle dynamics. Mol. Phys. 2021, 119, e1857863. [Google Scholar] [CrossRef]
- Petrus, P.; Lisal, M.; Brennan, J.K. Self-Assembly of Lamellar- and Cylinder-Forming Diblock Copolymers in Planar Slits: Insight from Dissipative Particle Dynamics Simulations. Langmuir 2010, 26, 14680–14693. [Google Scholar] [CrossRef] [PubMed]
- Posel, Z.; Posocco, P.; Lisal, M.; Fermeglia, M.; Pricl, S. Highly grafted polystyrene/polyvinylpyridine polymer gold nanoparticles in a good solvent: Effects of chain length and composition. Soft Matter 2016, 12, 3600–3611. [Google Scholar] [CrossRef] [PubMed]
- Seaton, M.A. DL_MESO_DPD: Development and use of mesoscale modelling software. Mol. Simul. 2021, 47, 228–247. [Google Scholar] [CrossRef]
- Prinsen, P.; Warren, P.B.; Michels, M.A.J. Mesoscale simulations of surfactant dissolution and mesophase formation. Phys. Rev. Lett. 2002, 89, 148302. [Google Scholar] [CrossRef] [PubMed]
- Milchev, A.; Bhattacharya, A.; Binder, K. Formation of block copolymer micelles in solution: A Monte Carlo study chain length dependence. Macromolecules 2001, 34, 1881–1893. [Google Scholar] [CrossRef]
- Balastre, M.; Li, F.; Schorr, P.; Yang, J.C.; Mays, J.W.; Tirrell, M.V. A study of polyelectrolyte brushes formed from adsorption of amphiphilic diblock copolymers using the surface forces apparatus. Macromolecules 2002, 35, 9480–9486. [Google Scholar] [CrossRef]














| Interaction Parameter aij | Bead A | Bead B | Wall Bead W | Solvent Bead S |
|---|---|---|---|---|
| Bead A | 25 | 37.5 | 25 | 25 |
| Bead B | 25 | 15 20 25 30 | 37.5 | |
| Wall bead W | 25 | 25 | ||
| Solvent bead S | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blovský, T.; Šindelka, K.; Limpouchová, Z.; Procházka, K. Self-Assembly of Symmetric Copolymers in Slits with Inert and Attractive Walls. Polymers 2023, 15, 4458. https://doi.org/10.3390/polym15224458
Blovský T, Šindelka K, Limpouchová Z, Procházka K. Self-Assembly of Symmetric Copolymers in Slits with Inert and Attractive Walls. Polymers. 2023; 15(22):4458. https://doi.org/10.3390/polym15224458
Chicago/Turabian StyleBlovský, Tomáš, Karel Šindelka, Zuzana Limpouchová, and Karel Procházka. 2023. "Self-Assembly of Symmetric Copolymers in Slits with Inert and Attractive Walls" Polymers 15, no. 22: 4458. https://doi.org/10.3390/polym15224458
APA StyleBlovský, T., Šindelka, K., Limpouchová, Z., & Procházka, K. (2023). Self-Assembly of Symmetric Copolymers in Slits with Inert and Attractive Walls. Polymers, 15(22), 4458. https://doi.org/10.3390/polym15224458