Next Article in Journal
Hydrothermal Ageing of Glass Fibre Reinforced Vinyl Ester Composites: A Review
Previous Article in Journal
4D Printing of Electroactive Triple-Shape Composites
Previous Article in Special Issue
Dynamic Fracture Resistance under Plane Strain Conditions of High-Density Polyethylene Nanoclay Composites
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Polymers
Volume 15
Issue 4
10.3390/polym15040833
polymers-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influence of the Chemical Structure on the Mechanical Relaxation of Dendrimers

by
Nadezhda N. Sheveleva
,
Andrei V. Komolkin
and
Denis A. Markelov
*
St. Petersburg State University, 7/9 Universitetskaya nab., 199034 St. Petersburg, Russia
*
Author to whom correspondence should be addressed.
Polymers 2023, 15(4), 833; https://doi.org/10.3390/polym15040833
Submission received: 16 December 2022 / Revised: 30 January 2023 / Accepted: 6 February 2023 / Published: 8 February 2023
(This article belongs to the Special Issue Mechanical and Advanced Properties of Polymers II)
Browse Figures
Versions Notes

Abstract

:
The rheological properties of macromolecules represent one of the fundamental features of polymer systems which expand the possibilities of using and developing new materials based on them. In this work, we studied the shear-stress relaxation of the second generation PAMAM and PPI dendrimer melts by atomistic molecular dynamics simulation. The time dependences of relaxation modulus G(t) and the frequency dependences of the storage G′(ω) and loss G″(ω) moduli were obtained. The results were compared with the similar dependences for the polycarbosilane (PCS) dendrimer of the same generation. The chemical structure of the dendrimer segments has been found to strongly influence their mechanical relaxation. In particular, it has been shown that hydrogen bonding in PAMAM dendrimers leads to an entanglement of macromolecules and the region is observed where G′(ω) > G″(ω). This slows down the mechanical relaxation and rotational diffusion of macromolecules. We believe that our comprehensive research contributes to the systematization of knowledge about the rheological properties of dendrimers.

Graphical Abstract

1. Introduction

Dendrimers are hyperbranched synthetic macromolecules with a perfectly symmetrical tree-like structure [1]. Dendrimers were first synthesized in the 70s [2], but recently they have attracted more attention from scientists [3,4]. The reason for this is the global demand for new nanomolecules and materials based on them, which can be used in advanced technologies [5,6] and medicine [7]. Therefore, the optimization of synthesis methods and the development of new strategies, that allow the creation of dendrimers with different morphology and functionalization, contribute to the emergence of new types of dendrimers [8,9,10]. The behavior of dendrimers in solution remains the most studied due to their use in biomedical applications [11,12,13] as nanocontainers for gene and drug delivery [14,15,16]. New developments are underway to create novel materials based on dendrimer macromolecules and to use dendrimers as nanomodifiers for already utilized materials [17,18].
The development of the theory of mechanical relaxation of dendrimers began with analytical studies using a simplified viscoelastic model [19,20,21,22,23,24,25,26,27,28,29]. However, within the framework of this model, it is quite difficult to predict the effects determined by volume interactions, the mobility of the dendrimer as a whole, and the intermacromolecular mobility/interactions, as well as the influence of the dendrimer chemical structure. Thus, in the first experimental rheological studies of dendrimers or hyperbranched polymers, the analysis of experimental data was usually carried out without taking into account the specific tree-like topology of macromolecules [30,31,32]. In the last decade, the experimental [33,34,35,36,37,38] and molecular dynamics simulation [39,40,41,42,43,44,45] studies have shown that melts of dendrimers of various architectures have unique properties (including rheological ones).
Among the huge variety of dendrimers, polycarbosilane dendrimers, due to the absence of specific interactions, e.g., ionic and hydrogen bonds, proved to be suitable for studying the role of dendrimer architecture on physical and dynamic properties and are used as model objects. In particular, the dendrimer architecture is reflected in the relaxation times, which can be associated with inner relaxation, as well as with the relaxation of branches as whole, following the qualitative assumptions of the theory [43,46,47,48,49]. Taking into account that the total relaxation of the dendrimer branches depends on their molecular weight, the spectrum of the corresponding relaxation times is wide.
Atomistic simulation of carbosilane dendrimer melts has been performed quite recently [41,43,50]. Other types of dendrimer melts were simulated in [42,44], and coarse-grained nonequilibrium molecular dynamics simulation was used to study the shear viscosity [51,52] and the rheological properties of dendrimer melts [53].
In the recent works, molecular dynamics simulations of functionalized [54] and non-functionalized [40] carbosilane dendrimers in melts have been carried out to study their mechanical properties. It has been shown [54], the fourth generation functionalized carbosilane dendrimers (FD) have a region where G′ > G″. As a rule, this effect is attributed to the presence of entanglements between polymers. However, the latter seems unlikely in the case of carbosilane dendrimers, since there are no specific interactions, and the size and molecular weight are insufficient for the physical entanglements. An analysis of the structural and equilibrium properties of FD suggests that the observed effect is due to the fact that dendrimer macromolecules are in a crowded environment caused by internal densification. It has been established that dynamic characteristics indicate the following manifestations of the crowded environment in FD G4: (i) the rotational diffusion of the dendrimer does not slow down and corresponds to the size of the dendrimer (i.e., the ratio of the rotation time of the dendrimer as a whole to the cube of the radius of gyration, τrot/Rg3, has similar values for FD G3 and G4; (ii) the terminal (maximal) mechanical relaxation time, τmax, increases significantly, e.g., the ratio τmax/τrot increases more than two times compared to FD G3.
On the other hand, in melts of hyperbranched polyglycerols (hbPG) with a high molecular weight, the entanglement effect was experimentally observed [55]. The authors of this Ref. [55] concluded that such macromolecules can form entanglements at a molecular weight, M, > 10,000 g/mol, which is significantly lower than the minimum M values required for linear polymer chains. It has been suggested that the main mechanism of entanglements is related to the formation of hydrogen bonds between macromolecules.
The aim of this work is a comprehensive study of the mechanical properties of dendrimers with different chemical structures, which have not yet been carried out. We consider the influence of the chemical structure on the mechanical relaxation of dendrimers. For this purpose, we have performed atomistic molecular dynamics (MD) simulations of polyamidoamine (PAMAM) and polypropylene imine (PPI) dendrimers of the second generation (G2) in a melt (see dendrimer structures in Figure 1). For comparative analysis, we use the MD simulation results for the polycarbosilane (PCS) dendrimer obtained by us earlier in [40].

2. Simulation Details and Theoretical Approach

In this work, we studied PAMAM and PPI dendrimers of the second generation (G2, with 16 terminal groups) in a melt using MD simulation. The atomistic model of united atoms was used, in which only ionized hydrogen atoms in NH2 groups were explicitly taken into account. The simulation box with periodic boundaries contained 27 dendrimers for each system. Molecular dynamics simulations were conducted with the GROMACS package [56] and the OPLS force field [57].
At the preliminary stage of equilibration, the systems were maintained at a constant temperature of 600 K with the V-rescale thermostat [58], which was triggered every 0.1 ps, and at a constant pressure of 1 atm by using the Berendsen barostat [59] with τp = 1 ps during 100 ns for PPI and 500 ns for PAMAM. The lengths of these trajectories were enough for the systems to “forget” the initial configurations. Then, each system was simulated in the NPT ensemble using the Langevin thermostat at different values of the coupling constant τT = 0.005, 0.05, and 0.5 ps in order to vary the friction in the system. For the highest value of τT, we simulated ten replicas in order to have better statistics at long times. Each system was equilibrated at least for 100 ns. The final trajectories were obtained in NVT ensemble during 600 ns for PPI and 1200 ns for PAMAM dendrimers.
To calculate the mechanical relaxation, we have used the method developed in Refs. [40,54]. The dynamical modulus G(t) is calculated from the fluctuations of the shear-stress tensor P ^ = ( P α β ) [60,61]
G ( t ) = V 30 k B T ∑ ( α β ) ( 6 〈 P α β ( t ) 〉 〈 P α β ( 0 ) 〉 + 〈 N α β ( t ) 〉 〈 N α β ( 0 ) 〉 )
where V is the box volume, T is the temperature, and kB is the Boltzmann constant, Nαβ = Pαα − Pββ, (αβ) sums over the xy, yz, and zx components of P ^ .
The resulting G(t) obtained at different values of the parameter τT are superimposed based on the rotational relaxation autocorrelation function,
P 1 r o t ( t ) = 〈 u → ( t ) × u → ( 0 ) 〉
where u → ( t ) is a unit vector connecting two nitrogen atoms, one nitrogen from the periphery and the other from the core. The exponential tail of the function P1rot(t) is characterized through the time τrot. The P1rot(t) related to different τT can be perfectly rescaled based on τrot. The same happens for G(t).

3. Results and Discussions

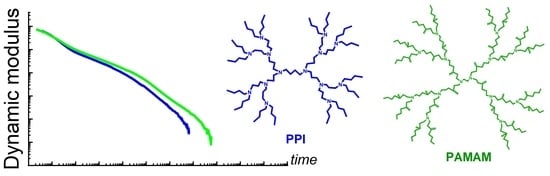
3.1. Relaxation Modulus

Figure 2 shows the time dependences of the relaxation moduli, G(t), for PAMAM G2 and PPI G2 dendrimers). For comparison, the G(t) dependence for PCS G2 is presented from our previous work (see [40]). As can be seen from this figure, the moduli G(t) of the studied dendrimers differ greatly from that one of PCS G2. In the region of tension relaxation, the slope of the G(t) dependences for PPI and PAMAM dendrimers is similar (−0.45 and −0.40, correspondingly), in contrast to −0.7 for PCS. In the case of PCS, the slope is determined by fluctuations in the x-component of the gyration tensor ⟨δRg,x2(t)⟩ ≡ ⟨[Rg,x(t) − Rg,x(0)]2⟩. The ⟨δRg,x2(t)⟩ functions for PPI and PAMAM are plotted on a double-logarithmic scale in Figure 3. A decrease in the slope of ⟨δRg,x2(t)⟩ can be observed for PPI and PAMAM to 0.57–0.58. Despite the different sizes of PPI and PAMAM dendrimers and the structures of their segments between branching points, the slopes of the G(t) dependences in the tension relaxation region and the slopes of ⟨δRg,x2(t)⟩ are almost the same. Apparently, this is due to the global conformations of PPI and PAMAM G2 in the melt, which differ significantly from PCS G2.
The radial density profiles (Figure 4) show that the PCS dendrimer has a significantly denser core than the PPI and PAMAM dendrimers. Accordingly, the chemical structure (Figure 1), the core of the PCS dendrimer, has a functionality of Fc = 4 (i.e., four segments are attached to the central silicon atom). As for PPI and PAMAM, the dendrimer core consists of two branching points (two nitrogen atoms) and formally has the functionality Fc = 2. Therefore, due to the less dense cores, the mutual penetration of PPI and PAMAM dendrimers into the center is significantly higher than in the case of PCS dendrimers. This apparently slows down the relaxation of G(t) at short times. It is important to note that with increasing generations, the difference in G(t) at short times between PCS and the studied dendrimers may considerably decrease or disappear, since the neighboring macromolecules of the PPI and PAMAM dendrimers will not be able to penetrate into the core region.
However, the slopes of the G(t) curves change more strongly than those of ⟨δRg,x2(t)⟩. We suggest that such a change is associated not only with fluctuations in the size of the dendrimer, but also with the formation of entanglements between macromolecules due to hydrogen bonding. In addition, according to the theory based on the viscoelastic model [23], an increase in the number of entanglements between dendrimers should lead to a slowdown in relaxation at short times. We will consider this issue in detail when analyzing the frequency dependences of the storage and loss moduli.
At an intermediate region, the inner relaxation spectrum is the main contributor to the G(t) dependence [40]. According to the theory, the inner spectrum is rather narrow and limited by times from 0.17τ0 to 5.8τ0, where τ0 is the relaxation time of an individual terminal segment. The segment length of the PAMAM dendrimer is significantly longer than that of the PPI dendrimer. Obviously, an increase in the segment length should lead to an increase in τ0 of the segment. In the case of PAMAM, this in turn leads to a shift of the inner relaxation region towards longer times and a slower decay of the G(t) curve compared to PPI and PCS.
Further along the time scale, the G(t) dependence is determined by branch relaxation. At low generations, the branch relaxation spectrum in PCS manifests weakly compared to G > 2 (see Ref. [40]), since its characteristic times correspond to the motions of branches and/or sub-branches as a whole.
According to the theory [23], in the case of G = 2, there are only two non-degenerate times except the characteristic relaxation time of the terminal segment (i.e., τ0). This leads to a rather narrow region of branch relaxation. A similar situation is observed for PPI. However, for PAMAM, the branch relaxation region is broadened. This can be explained by the presence of entanglements within the PAMAM dendrimer due to hydrogen bonding between groups of neighboring branches/sub-branches (see Table 1). In the PAMAM dendrimer, the average number of intramolecular hydrogen bonds is 7.5, while they are absent in PPI and PCS.
At longer times, mechanical relaxation is determined by the mobility of the dendrimer as a whole and/or interactions between the dendrimer macromolecules. To analyze the relaxation of G(t) in this region, we used the single-exponential fitting (i.e., ~exp(−2t/τmax), where τmax is the terminal (maximal) relaxation time of the G(t) dependence). The τmax values are shown in Table 1 for all the dendrimers under consideration. It can be seen from this table that the time τmax for PAMAM G2 is almost an order of magnitude longer than for the other dendrimers.
In order to compare the rotational diffusion and the maximal relaxation time we consider the ratio τmax/τrot. For all the dendrimers, the ratios τmax/τrot have similar values. Therefore, for the studied dendrimers, the mechanical relaxation of the macromolecule as a whole corresponds to its rotational mobility. It is important to note that for PCS at G > 2, this ratio increases, which indicates a slowdown in mechanical relaxation compared to rotational diffusion of dendrimers caused by the crowded environment [54]. Thus, the difference in τmax for PAMAM G2 and for other considered dendrimers is not related to this effect.
We also calculated the ratio τrot/Rg3 in order to take into account the difference in the sizes of dendrimers (i.e., in Rg) [54,62]. However, when using the equilibrium parameter (Rg3) to calibrate τrot, the parameter B increases slightly for PPI and more than 5 times for PAMAM compared to PCS. We believe that this is caused by entanglements between dendrimers due to the formation of intermolecular hydrogen bonds, of which there are on average two in PPI and 11 in PAMAM dendrimer melts. This slows down both the maximal mechanical relaxation time and the rotational diffusion of the macromolecule.

3.2. Storage and Loss Moduli

Figure 5 shows the frequency dependences of the storage G′(ω) and loss G″(ω) moduli for the dendrimer melts under consideration. The growth of G′(ω) and G″(ω) in the low-frequency region is determined by τmaxω2 and τmaxω, correspondingly. Therefore, the fastest growth in this region is observed for PAMAM. The G′(ω) and G″(ω) curves for PPI and PCS differ slightly.
In the mid-frequency range, all G″(ω) and G′(ω) curves do not intersect and have slopes of 0.66 and 0.69, respectively. These values are quite similar to the slope of 0.7 obtained experimentally for PPI dendrimers G = 3–5 (G = 2–4 in our numbering) [34]. For a more detailed comparison with experiment, MD simulation of higher generation dendrimers is required, which will be carried out in the near future.
It is important to note that in the case of FD G4, in this frequency range (106–108 rad/s), a region was observed where G′(ω) > G″(ω). Moreover, the latter is due to the effect of a crowded environment, and not the entanglement of macromolecules as, e.g., in linear polymers. In the case of PAMAM G2, the G′(ω) > G″(ω) region is also observed (Figure 5c), but it is narrower and shifted to the high-frequency region (2 × 1011–4 × 1012 rad/s). However, in the case of PPI G2, there is no such region. We believe that this effect is associated with entanglements between dendrimers due to hydrogen bonds, which are quite numerous in PAMAM G2 and practically absent in PPI G2 (see Table 1). The hydrogen bonds were calculated in GROMACS package using standard tools for their analysis. The main parameters for calculating hydrogen bonds were as follows: the hydrogen bond length (i.e., distance between the donor and acceptor) is no more than 0.35 nm, and the hydrogen bond angle (acceptor-donor-hydrogen) is no more than 30 degrees. The distributions of hydrogen bond lengths and angles are shown in Figure 6. It can be seen from this figure that the most probable hydrogen bond length in the PAMAM dendrimer is less than 0.3 nm and the largest number of bonds has an angle of about 15 degrees. These results confirm the presence of hydrogen bonds between the PAMAM dendrimer macromolecules in the melt. However, it is important to note that the simulations were carried out at 600 K, which greatly shortens the average lifetime of hydrogen bonds. According to our estimates, it does not exceed 50 ps.
In this regard, the experimental results obtained for multiarm star polymers with a dendrimer core [63] are of interest, since the hallmarks of both crowded environment and entanglement effects manifest in these systems. Moreover, compared to entanglements, the effect of crowded environment (in this case, jamming) is exhibited in the low-frequency region. This means that our assumptions about the different nature of the G′(ω) > G″(ω) region for PAMAM G2 and FD G4 are in qualitative agreement with the results of [63]. Thus, the different nature of this region for FD G4 and PAMAM G2 allows us to conclude that these effects manifest themselves in the dynamic characteristics: (i) the crowded environment effect slows down the mechanical relaxation, but at the same time has little impact on the rotational diffusion of the dendrimer; (ii) the entanglement effect slows down both rotational diffusion and mechanical relaxation.
As can be seen from Figure 5, in the high-frequency region, the G′(ω) and G″(ω) dependences for the studied dendrimers differ from those for PCS. As in the case of the time dependence G(t) at short times, these differences are associated with two factors: (i) the PAMAM and PPI dendrimers have less dense cores (with Fc = 2) compared to the PCS dendrimer (with Fc = 4) which facilitates the mutual penetration of dendrimer macromolecules (see Figure 4); (ii) the presence of entanglements between the dendrimers due to the formation of hydrogen bonds. The first factor leads to a change in the fluctuation of the dendrimer size: the slope of ⟨δRg,x2(t)⟩ at short times varies from 0.7 (for PCS) to 0.57–0.58 (for PAMAM and PPI). The second factor affects the slope of G′(ω) and G″(ω) in the high-frequency region. According to the viscoelastic theory [23], an increase in the number of entanglements between dendrimers leads to a slowdown in the growth of both G′(ω) and G″(ω) in the high-frequency region. Our results are in qualitative agreement with the theory. Since the number of entanglements between dendrimer macromolecules in the PAMAM melt is significantly greater (see Table 1), the slope of G′(ω) and G″(ω) in the high-frequency region for PAMAM decreases more strongly (up to 0.4) than for PPI (up to 0.45).

4. Conclusions

The melts of PPI and PAMAM dendrimers of the second generation (G = 2, with 16 terminal groups) were studied using molecular dynamics simulation. The aim of the work was to study the influence of the chemical structure of the dendrimer on mechanical relaxation. Moreover, for comparison, we used the previously obtained results for PCS G2.
It has been shown that the mechanical relaxation in the tension relaxation region (at high frequencies or short times) of PPI and PAMAM G2 is very different from PCS G2. This is due to the less dense core of PPI and PAMAM than that in PCS, as well as the entanglements between dendrimers due to hydrogen bonds, which are absent in PCS. In this regard, a significant change in the absolute value of the slope of the dynamic modulus from 0.7 (for PCS G2) to 0.4–0.45 (for PPI and PAMAM G2) is observed. However, it is most likely that, for higher generations, the difference in G(t) at short times between PCS and the studied dendrimers may significantly decrease or disappear, since the neighboring PPI and PAMAM dendrimer macromolecules will not be able to penetrate into the core region.
In the intermediate and high-frequency regions, the mechanical relaxation of PAMAM slows down compared to PPI and PCS. Moreover, as for PAMAM, the region is observed where G′(ω) > G″(ω). This effect is associated with the presence of intermolecular entanglements due to hydrogen bonding. The entanglement between PAMAM dendrimers is also confirmed by the slowdown of rotational diffusion.
Thus, hydrogen bonding strongly affects the mechanical relaxation of dendrimer melts. Therefore, tuning the chemical structure of the dendrimer can be used to control the mechanical properties. We believe that our comprehensive research contributes to the targeted synthesis of dendrimer macromolecules with tailored mechanical properties and the systematization of knowledge about their rheological properties.

Author Contributions

Conceptualization, D.A.M. and N.N.S.; methodology, D.A.M. and N.N.S.; validation, N.N.S., A.V.K. and D.A.M.; formal analysis, N.N.S., A.V.K. and D.A.M.; investigation, N.N.S., A.V.K. and D.A.M.; writing—original draft preparation, N.N.S.; writing—review and editing, N.N.S., A.V.K. and D.A.M.; visualization, N.N.S.; supervision, N.N.S. and D.A.M.; funding acquisition, N.N.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the Russian Science Foundation (No. 21-73-00067).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The authors thank Maxim Dolgushev (LPTMC, Sorbonne Université) for fruitful discussions. The simulations were performed the Computer Resources Center of Saint Petersburg State University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mintzer, M.A.; Grinstaff, M.W. Biomedical applications of dendrimers: A tutorial. Chem. Soc. Rev. 2011, 40, 173–190. [Google Scholar] [CrossRef] [PubMed]
  2. Buhleier, E.; Wehner, W.; Voegtle, F. “Cascade”-And “Nonskid-chain-like” Syntheses of Molecular Cavity Topologies. Synthesis Stuttg. 1978, 2, 155–158. [Google Scholar] [CrossRef]
  3. Astruc, D.; Boisselier, E.; Ornelas, C. Dendrimers Designed for Functions: From Physical, Photophysical, and Supramolecular Properties to Applications in Sensing, Catalysis, Molecular Electronics, Photonics, and Nanomedicine. Chem. Rev. 2010, 110, 1857–1959. [Google Scholar] [CrossRef]
  4. Newkome, G.R.; Shreiner, C. Dendrimers Derived from 1 → 3 Branching Motifs. Chem. Rev. 2010, 110, 6338–6442. [Google Scholar] [PubMed]
  5. Yamamoto, K.; Imaoka, T.; Tanabe, M.; Kambe, T. New Horizon of Nanoparticle and Cluster Catalysis with Dendrimers. Chem. Rev. 2020, 120, 1397–1437. [Google Scholar] [CrossRef] [PubMed]
  6. Markelov, D.A.; Semisalova, A.S.; Mazo, M.A. Formation of a Hollow Core in Dendrimers in Solvents. Macromol. Chem. Phys. 2021, 222, 2100085. [Google Scholar] [CrossRef]
  7. Kim, Y.; Park, E.J.; Na, D.H. Recent progress in dendrimer-based nanomedicine development. Arch. Pharm. Res. 2018, 41, 571–582. [Google Scholar] [CrossRef]
  8. Sowinska, M.; Urbanczyk-Lipkowska, Z. Advances in the chemistry of dendrimers. New J. Chem. 2014, 38, 2168. [Google Scholar] [CrossRef]
  9. Kang, T.; Amir, R.J.; Khan, A.; Ohshimizu, K.; Hunt, J.N.; Sivanandan, K.; Montañez, M.I.; Malkoch, M.; Ueda, M.; Hawker, C.J. Facile access to internally functionalized dendrimers through efficient and orthogonal click reactions. Chem. Commun. 2010, 46, 1556–1558. [Google Scholar] [CrossRef] [PubMed]
  10. Hecht, S. Functionalizing the interior of dendrimers: Synthetic challenges and applications. J. Polym. Sci. Part A Polym. Chem. 2003, 41, 1047–1058. [Google Scholar] [CrossRef]
  11. Chis, A.A.; Dobrea, C.; Morgovan, C.; Arseniu, A.M.; Rus, L.L.; Butuca, A.; Juncan, A.M.; Totan, M.; Vonica-Tincu, A.L.; Cormos, G.; et al. Applications and Limitations of Dendrimers in Biomedicine. Molecules 2020, 25, 3982. [Google Scholar] [CrossRef] [PubMed]
  12. Dias, A.P.; da Silva Santos, S.; da Silva, J.V.; Parise-Filho, R.; Igne Ferreira, E.; El Seoud, O.; Giarolla, J. Dendrimers in the context of nanomedicine. Int. J. Pharm. 2020, 573, 118814. [Google Scholar] [CrossRef]
  13. Gorzkiewicz, M.; Konopka, M.; Janaszewska, A.; Tarasenko, I.I.; Sheveleva, N.N.; Gajek, A.; Neelov, I.M.; Klajnert-Maculewicz, B. Application of new lysine-based peptide dendrimers D3K2 and D3G2 for gene delivery: Specific cytotoxicity to cancer cells and transfection in vitro. Bioorg. Chem. 2020, 95, 103504. [Google Scholar] [CrossRef] [PubMed]
  14. Hsu, H.; Bugno, J.; Lee, S.; Hong, S. Dendrimer-based nanocarriers: A versatile platform for drug delivery. WIREs Nanomed. Nanobiotechnology 2017, 9, 1–21. [Google Scholar] [CrossRef]
  15. Cheng, Y.; Xu, Z.; Ma, M.; Xu, T. Dendrimers as Drug Carriers: Applications in Different Routes of Drug Administration. J. Pharm. Sci. 2008, 97, 123–143. [Google Scholar] [CrossRef] [PubMed]
  16. Dubey, S.K.; Salunkhe, S.; Agrawal, M.; Kali, M.; Singhvi, G.; Tiwari, S.; Saraf, S.; Saraf, S.; Alexander, A. Understanding the Pharmaceutical Aspects of Dendrimers for the Delivery of Anticancer Drugs. Curr. Drug Targets 2020, 21, 528–540. [Google Scholar] [CrossRef]
  17. Kuang, T.; Chang, L.; Fu, D.; Yang, J.; Zhong, M.; Chen, F.; Peng, X. Improved crystallizability and processability of ultra high molecular weight polyethylene modified by poly(amido amine) dendrimers. Polym. Eng. Sci. 2017, 57, 153–160. [Google Scholar] [CrossRef]
  18. Zhao, H.; Liao, B.; Nian, F.; Zhao, Y.; Wang, K.; Pang, H. Synthesis and characterization of a PAMAM dendrimer-based superplasticizer and its effect on the properties in cementitious system. J. Appl. Polym. Sci. 2018, 135, 1–11. [Google Scholar] [CrossRef]
  19. Gotlib, Y.Y.; Markelov, D.A. Theory of the Relaxation Spectrum of a Dendrimer Macromolecule. Polym. Sci. Ser. A 2002, 44, 1341–1350. [Google Scholar]
  20. Cai, C.; Chen, Z.Y. Rouse Dynamics of a Dendrimer Model in the ϑ Condition. Macromolecules 1997, 30, 5104–5117. [Google Scholar] [CrossRef]
  21. Grimm, J.; Dolgushev, M. Dynamics of internally functionalized dendrimers. Phys. Chem. Chem. Phys. 2016, 18, 19050–19061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Biswas, P.; Kant, R.; Blumen, A. Polymer dynamics and topology: Extension of stars and dendrimers in external fields. Macromol. Theory Simul. 2000, 9, 56–67. [Google Scholar] [CrossRef]
  23. Gurtovenko, A.A.; Markelov, D.A.; Gotlib, Y.Y.; Blumen, A. Dynamics of dendrimer-based polymer networks. J. Chem. Phys. 2003, 119, 7579–7590. [Google Scholar] [CrossRef]
  24. Blumen, A.; Gurtovenko, A.A. Generalized Gaussian Structures: Models for Polymer Systems with Complex Topologies. Adv. Polym. Sci. 2005, 182, 171–282. [Google Scholar]
  25. Dolgushev, M.; Blumen, A. Dynamics of semiflexible treelike polymeric networks. J. Chem. Phys. 2009, 131, 044905. [Google Scholar] [CrossRef] [PubMed]
  26. Dolgushev, M.; Blumen, A. Dynamics of Semiflexible Chains, Stars, and Dendrimers. Macromolecules 2009, 42, 5378–5387. [Google Scholar] [CrossRef]
  27. Markelov, D.A.; Lähderanta, E.; Gotlib, Y.Y. Influence of Modified Terminal Segments on Dynamic Modulus and Viscosity of Dendrimer. Macromol. Theory Simul. 2010, 19, 158–169. [Google Scholar] [CrossRef]
  28. Dolgushev, M.; Blumen, A. Dynamics of chains and dendrimers with heterogeneous semiflexibility. J. Chem. Phys. 2010, 132, 124905. [Google Scholar] [CrossRef]
  29. Dolgushev, M.; Berezovska, G.; Blumen, A. Branched semiflexible polymers: Theoretical and simulation aspects. Macromol. Theory Simulations 2011, 20, 621–644. [Google Scholar] [CrossRef]
  30. Uppuluri, S.; Morrison, F.A.; Dvornic, P.R. Rheology of dendrimers. 2. Bulk polyamidoamine dendrimers under steady shear, creep, and dynamic oscillatory shear. Macromolecules 2000, 33, 2551–2560. [Google Scholar] [CrossRef]
  31. Kwak, S.-Y.; Ahn, D.U. Processability of Hyperbranched Poly(ether ketone)s with Different Degrees of Branching from Viewpoints of Molecular Mobility and Comparison with Their Linear Analogue. Macromolecules 2000, 33, 7557–7563. [Google Scholar] [CrossRef]
  32. Wu, W.; Driessen, W.; Jiang, X. Oligo(ethylene glycol)-Based Thermosensitive Dendrimers and Their Tumor Accumulation and Penetration. J. Am. Chem. Soc. 2014, 136, 3145–3155. [Google Scholar] [CrossRef] [PubMed]
  33. Milenin, S.A.; Selezneva, E.V.; Tikhonov, P.A.; Vasil’ev, V.G.; Buzin, A.I.; Balabaev, N.K.; Kurbatov, A.O.; Petoukhov, M.V.; Shtykova, E.V.; Feigin, L.A.; et al. Hybrid Polycarbosilane-Siloxane Dendrimers: Synthesis and Properties. Polymers 2021, 13, 606. [Google Scholar] [CrossRef] [PubMed]
  34. Hofmann, M.; Gainaru, C.; Cetinkaya, B.; Valiullin, R.; Fatkullin, N.; Rössler, E.A. Field-Cycling Relaxometry as a Molecular Rheology Technique: Common Analysis of NMR, Shear Modulus and Dielectric Loss Data of Polymers vs Dendrimers. Macromolecules 2015, 48, 7521–7534. [Google Scholar] [CrossRef]
  35. Mohamed, F.; Hofmann, M.; Pötzschner, B.; Fatkullin, N.; Rössler, E.A. Dynamics of PPI Dendrimers: A Study by Dielectric and H-2 NMR Spectroscopy and by Field-Cycling H-1 NMR Relaxometry. Macromolecules 2015, 48, 3294–3302. [Google Scholar] [CrossRef]
  36. Vasil’ev, V.G.; Kramarenko, E.Y.; Tatarinova, E.A.; Milenin, S.A.; Kalinina, A.A.; Papkov, V.S.; Muzafarov, A.M. An unprecedented jump in the viscosity of high-generation carbosilane dendrimer melts. Polymer Guildf. 2018, 146, 1–5. [Google Scholar] [CrossRef]
  37. Sendijarevic, I.; McHugh, A.J. Effects of Molecular Variables and Architecture on the Rheological Behavior of Dendritic Polymers. Macromolecules 2000, 33, 590–596. [Google Scholar] [CrossRef]
  38. Matveev, V.V.; Markelov, D.A.; Dvinskikh, S.V.; Shishkin, A.N.; Tyutyukin, K.V.; Penkova, A.V.; Tatarinova, E.A.; Ignat’Eva, G.M.; Milenin, S.A. Investigation of Melts of Polybutylcarbosilane Dendrimers by 1H NMR Spectroscopy. Sci. Rep. 2017, 7, 13710. [Google Scholar] [CrossRef]
  39. Karatasos, K. Static and Dynamic Behavior in Model Dendrimer Melts:  Toward the Glass Transition. Macromolecules 2005, 38, 4472–4483. [Google Scholar] [CrossRef]
  40. Dolgushev, M.; Markelov, D.A.; Lähderanta, E. Linear Viscoelasticity of Carbosilane Dendrimer Melts. Macromolecules 2019, 52, 2542–2547. [Google Scholar] [CrossRef]
  41. Balabaev, N.K.; Mazo, M.A.; Kramarenko, E.Y. Insight into the Structure of Polybutylcarbosilane Dendrimer Melts via Extensive Molecular Dynamics Simulations. Macromolecules 2017, 50, 432–445. [Google Scholar] [CrossRef]
  42. Bag, S.; Jain, M.; Maiti, P.K. Charge Transport in Dendrimer Melts Using Multiscale Modeling Simulation. J. Phys. Chem. B 2016, 120, 9142–9151. [Google Scholar] [CrossRef] [Green Version]
  43. Markelov, D.A.; Shishkin, A.N.; Matveev, V.V.; Penkova, A.V.; Lähderanta, E.; Chizhik, V.I. Orientational Mobility in Dendrimer Melts: Molecular Dynamics Simulations. Macromolecules 2016, 49, 9247–9257. [Google Scholar] [CrossRef]
  44. Smeijers, A.F.; Markvoort, A.J.; Pieterse, K.; Hilbers, P.A.J. Coarse-grained simulations of poly(propylene imine) dendrimers in solution. J. Chem. Phys. 2016, 144, 074903. [Google Scholar] [CrossRef] [PubMed]
  45. Kurbatov, A.O.; Balabaev, N.K.; Mazo, M.A.; Kramarenko, E.Y. Effects of generation number, spacer length and temperature on the structure and intramolecular dynamics of siloxane dendrimer melts: Molecular dynamics simulations. Soft Matter 2020, 16, 3792–3805. [Google Scholar] [CrossRef]
  46. Gotlib, Y.Y.; Markelov, D.A. Permittivity of a dendrimer containing polar groups. Polym. Sci. Ser. A 2004, 46, 815–832. [Google Scholar]
  47. Gotlib, Y.Y.; Markelov, D.A. Theory of orientational relaxation of individual specified units in a dendrimer. Polym. Sci. Ser. A 2007, 49, 1137–1154. [Google Scholar] [CrossRef]
  48. Markelov, D.A.; Dolgushev, M.; Gotlib, Y.Y.; Blumen, A. NMR relaxation of the orientation of single segments in semiflexible dendrimers. J. Chem. Phys. 2014, 140, 244904. [Google Scholar] [CrossRef]
  49. Markelov, D.A.; Dolgushev, M.; Lähderanta, E. Chapter One—NMR Relaxation in Dendrimers. In Annual Reports on NMR Spectroscopy; Webb, G.A., Ed.; Academic Press: Cambridge, MA, USA, 2017; Volume 91, pp. 1–66. ISBN 0066-4103. [Google Scholar]
  50. Shishkin, A.N.; Markelov, D.A.; Matveev, V.V. Molecular dynamics simulation of poly(butyl)carbosilane dendrimer melts at 600 K. Russ. Chem. Bull. 2016, 65, 67–74. [Google Scholar] [CrossRef]
  51. Bosko, J.T.; Todd, B.D.; Sadus, R.J. Viscoelastic properties of dendrimers in the melt from nonequlibrium molecular dynamics. J. Chem. Phys. 2004, 121, 12050–12059. [Google Scholar] [CrossRef] [PubMed]
  52. Bosko, J.T.; Todd, B.D.; Sadus, R.J. Molecular simulation of dendrimers and their mixtures under shear: Comparison of isothermal-isobaric (NpT) and isothermal-isochoric (NVT) ensemble systems. J. Chem. Phys. 2005, 123, 034905. [Google Scholar] [CrossRef] [PubMed]
  53. Hajizadeh, E.; Todd, B.D.; Daivis, P.J. Nonequilibrium molecular dynamics simulation of dendrimers and hyperbranched polymer melts undergoing planar elongational flow. J. Rheol. 2014, 58, 281–305. [Google Scholar] [CrossRef]
  54. Sheveleva, N.N.; Dolgushev, M.; Lähderanta, E.; Markelov, D.A. Mechanical relaxation of functionalized carbosilane dendrimer melts. Phys. Chem. Chem. Phys. 2022, 24, 13049–13056. [Google Scholar] [CrossRef] [PubMed]
  55. Schubert, C.; Osterwinter, C.; Tonhauser, C.; Schömer, M.; Wilms, D.; Frey, H.; Friedrich, C. Can hyperbranched polymers entangle? Effect of hydrogen bonding on entanglement transition and thermorheological properties of hyperbranched polyglycerol melts. Macromolecules 2016, 49, 8722–8737. [Google Scholar] [CrossRef]
  56. Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
  57. Matsui, M.; Akaogi, M. Molecular Dynamics Simulation of the Structural and Physical Properties of the Four Polymorphs of TiO2. Mol. Simul. 1991, 6, 239–244. [Google Scholar] [CrossRef]
  58. Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
  59. Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
  60. Ramírez, J.; Sukumaran, S.K.; Vorselaars, B.; Likhtman, A.E. Efficient on the fly calculation of time correlation functions in computer simulations. J. Chem. Phys. 2010, 133, 154103. [Google Scholar] [CrossRef]
  61. David, A.; De Nicola, A.; Tartaglino, U.; Milano, G.; Raos, G. Viscoelasticity of Short Polymer Liquids from Atomistic Simulations. J. Electrochem. Soc. 2019, 166, B3246–B3256. [Google Scholar] [CrossRef]
  62. Tsvetkov, V.N. Structure and properties of rigid chain polymer molecules in solutions. Polym. Sci. U.S.S.R. 1979, 21, 2879–2899. [Google Scholar] [CrossRef]
  63. Gury, L.; Gauthier, M.; Cloitre, M.; Vlassopoulos, D. Colloidal Jamming in Multiarm Star Polymer Melts. Macromolecules 2019, 52, 4617–4623. [Google Scholar] [CrossRef]
Polymers 15 00833 g001 550
Figure 1. Structures of the second generation dendrimers (G = 2, with 16 terminal groups) (a) polyamidoamine (PAMAM), (b) polypropylene imine (PPI) and (c) polycarbosilane (PCS) dendrimers. g is the generation layer number.
Figure 1. Structures of the second generation dendrimers (G = 2, with 16 terminal groups) (a) polyamidoamine (PAMAM), (b) polypropylene imine (PPI) and (c) polycarbosilane (PCS) dendrimers. g is the generation layer number.
Polymers 15 00833 g001
Polymers 15 00833 g002 550
Figure 2. Double-logarithmic representation of the normalized shear-stress relaxation moduli [G(t)] = G(t)/G(0) for PAMAM and PPI dendrimer melts. For comparison the data for PCS melt are adapted with permission from Ref. [40]. 2019, American Chemical Society.
Figure 2. Double-logarithmic representation of the normalized shear-stress relaxation moduli [G(t)] = G(t)/G(0) for PAMAM and PPI dendrimer melts. For comparison the data for PCS melt are adapted with permission from Ref. [40]. 2019, American Chemical Society.
Polymers 15 00833 g002
Polymers 15 00833 g003 550
Figure 3. Fluctuations of the x-component of the gyration tensor ⟨δRg,x2(t)⟩ ≡ ⟨[Rg,x(t) − Rg,x(0)]2⟩ for the dendrimers. For comparison the data for PCS melt are adapted with permission from Ref. [40]. 2019, American Chemical Society.
Figure 3. Fluctuations of the x-component of the gyration tensor ⟨δRg,x2(t)⟩ ≡ ⟨[Rg,x(t) − Rg,x(0)]2⟩ for the dendrimers. For comparison the data for PCS melt are adapted with permission from Ref. [40]. 2019, American Chemical Society.
Polymers 15 00833 g003
Polymers 15 00833 g004 550
Figure 4. The radial density profiles from the center of mass of the macromolecule both for selected dendrimer, ρD, (solid) and for the rest of the dendrimers in the system, ρoverlap, (dashed) using the formula: ρ ( r ) = < m ( r ) > / V ( r ) , where ρ(r) is the average density in the spherical layer at a distance r from the dendrimer’s center of mass, <m(r)> is the average total mass of atoms in the layer of volume V(r).
Figure 4. The radial density profiles from the center of mass of the macromolecule both for selected dendrimer, ρD, (solid) and for the rest of the dendrimers in the system, ρoverlap, (dashed) using the formula: ρ ( r ) = < m ( r ) > / V ( r ) , where ρ(r) is the average density in the spherical layer at a distance r from the dendrimer’s center of mass, <m(r)> is the average total mass of atoms in the layer of volume V(r).
Polymers 15 00833 g004
Polymers 15 00833 g005 550
Figure 5. Double-logarithmic representation of the storage [G′(ω)] (a) and loss [G″(ω)] (b) moduli for PAMAM and PPI melts are plotted together; (c,d) separately for PAMAM and PPI, respectively. For comparison the data for PCS melt are adapted with permission from Ref. [40]. 2019, American Chemical Society.
Figure 5. Double-logarithmic representation of the storage [G′(ω)] (a) and loss [G″(ω)] (b) moduli for PAMAM and PPI melts are plotted together; (c,d) separately for PAMAM and PPI, respectively. For comparison the data for PCS melt are adapted with permission from Ref. [40]. 2019, American Chemical Society.
Polymers 15 00833 g005
Polymers 15 00833 g006 550
Figure 6. The hydrogen bond length (a) and angle (b) distributions in PAMAM G2 dendrimers in the melt.
Figure 6. The hydrogen bond length (a) and angle (b) distributions in PAMAM G2 dendrimers in the melt.
Polymers 15 00833 g006
Table
Table 1. Structural and dynamic characteristics of the second generation PAMAM, PPI and PSC dendrimers. The number of terminal groups, Nter, the molecular weight, M, the radius of gyration, Rg, the rotational relaxation time, τrot. The terminal (maximal) time of mechanical relaxation, τmax, characterizing the tail of the relaxation modulus of dendrimers (G(t) ~exp(−2t/τmax)). The average number of hydrogen bonds per one dendrimer, <NHB>, within the macromolecule (intra) and number of external hydrogen bonds between macromolecules (inter). Note that the intramolecular hydrogen bond is counted twice (for the donor and acceptor) per dendrimer, as well as the intermolecular hydrogen bond.
Table 1. Structural and dynamic characteristics of the second generation PAMAM, PPI and PSC dendrimers. The number of terminal groups, Nter, the molecular weight, M, the radius of gyration, Rg, the rotational relaxation time, τrot. The terminal (maximal) time of mechanical relaxation, τmax, characterizing the tail of the relaxation modulus of dendrimers (G(t) ~exp(−2t/τmax)). The average number of hydrogen bonds per one dendrimer, <NHB>, within the macromolecule (intra) and number of external hydrogen bonds between macromolecules (inter). Note that the intramolecular hydrogen bond is counted twice (for the donor and acceptor) per dendrimer, as well as the intermolecular hydrogen bond.
DendrimerNterMd, g/molRg, nm<NHB>τrot, nsτmax, nsτrot/Rg3,
ns nm−3		τmax/τrot
intrainter
PAMAM163256.21.03410.97.57.9164.0887.160.52
PPI161686.80.873201.0740.5121.610.46
PCS161964.30.872000.8310.4611.250.55
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sheveleva, N.N.; Komolkin, A.V.; Markelov, D.A. Influence of the Chemical Structure on the Mechanical Relaxation of Dendrimers. Polymers 2023, 15, 833. https://doi.org/10.3390/polym15040833

AMA Style

Sheveleva NN, Komolkin AV, Markelov DA. Influence of the Chemical Structure on the Mechanical Relaxation of Dendrimers. Polymers. 2023; 15(4):833. https://doi.org/10.3390/polym15040833

Chicago/Turabian Style

Sheveleva, Nadezhda N., Andrei V. Komolkin, and Denis A. Markelov. 2023. "Influence of the Chemical Structure on the Mechanical Relaxation of Dendrimers" Polymers 15, no. 4: 833. https://doi.org/10.3390/polym15040833

APA Style

Sheveleva, N. N., Komolkin, A. V., & Markelov, D. A. (2023). Influence of the Chemical Structure on the Mechanical Relaxation of Dendrimers. Polymers, 15(4), 833. https://doi.org/10.3390/polym15040833

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop