A Design-Oriented Combined Model (7 MPa to 190 MPa) for FRP-Confined Circular Short Columns
Abstract
:1. Introduction
2. Strength and Strain Models for FRP Confinement
2.1. Confinement with FRP

| Source | Strength Model | Strain Model |
|---|---|---|
| Fardis and Khalili [2] strength model based on Richart et al. [36] (fco = 20–50 MPa) | ||
| Mander et al. [37] Saadatmanesh et al. [38] | ||
| ACI 440 [39] | ||
| Karbhari and Gao [5] (fco = 38 MPa) | Model II | |
| Kono et al. [40] (fco = 32–35 MPa) | ||
| Saafi et al. [41] (fco = 38 MPa) | ||
| Spoelstra and Monti [33] (fco = 30–50 MPa) | a | |
| Xiao and Wu [42] (fco = 34–55 MPa, CFRP) | ||
| Toutanji-modified [43] (fco = 31 MPa) | ||
| Lam and Teng [30] (fco = 27–55 MPa) | ||
| Teng et al. [44] (fco = 38–46 MPa) | ||
| Benzaid et al. [31] (fco = 29–62 MPa, CFRP) | ||
| Rousakis et al. [45,46] (fco = 9–170 MPa) | b | |
| Ozbakkaloglu and Lim [32] | ||
2.2. Strength Models
| Reference | Failure Criterion for Rock | Modified Form for FRP Confined Concrete |
|---|---|---|
| Girgin [29] | Hoek-Brown et al. [27] ≥ 20 MPa | s = 1 for intact rock or undamaged concrete m = 2.9 (fco = 7 to18 MPa) m = 6.34−0.076 fco (fco = 20 to 82 MPa) m = 0.1 (fco = 82 to 108 MPa) |
| Girgin [48] | Johnston [47] | , fco in kPa (fco = 7 to 24 MPa) (fco = 25 to 108 MPa) |
2.3. Strain Models
3. Results and Discussion
3.1. Ultimate Strength Prediction

3.2. Ultimate Strain Prediction

| Parameter | Strain Models | Range of Data | n | IAE % | AAE % | Figures | |
|---|---|---|---|---|---|---|---|
| Models for CFRP sheets | |||||||
| Ia | 15 MPa ≤ fco ≤ 50 MPa a 0.11 ≤ fl/fco ≤ 1.78 | 102 | 13.3 | 13.5 | - | ||
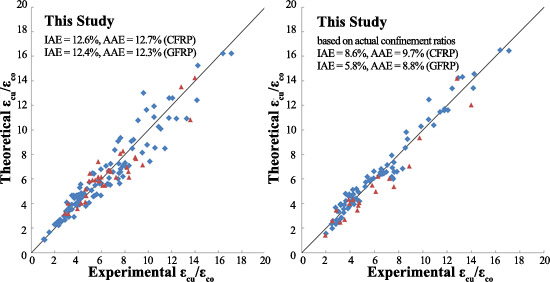
| Ib | 15 MPa ≤ fco ≤ 50 MPa 0.11 ≤ fl/fco ≤ 1.78 | 102 | 12.6 | 13.1 | Figure 4a | ||
| II | 50 MPa < fco ≤ 103 MPa 0.12 ≤ fl/fco ≤ 0.58 | 45 | 11.7 | 11.0 | |||
| III | 109 MPa <fco ≤ 170 MPa b 0.07 ≤ fl/fco ≤ 0.87 | 10 | 5.7 | 6.2 | |||
| IV | 20 MPa < fco ≤ 103 MPa 0.03 ≤ fl,a/fco ≤ 1.01 | 96 | 8.6 | 9.7 | Figure 4b | ||
| Models for GFRP sheets | |||||||
| V | 18 MPa ≤ fco ≤ 50 MPa 0.09 ≤ fl/fco ≤ 2.0 | 33 | 13.4 | 12.3 | Figure 4a | ||
| VI | 80 MPa < fco ≤ 159 MPa 0.1≤ fl/fco ≤ 0.6 | 10 | 11.9 | 12.3 | |||
| VII | 18 MPa ≤ fco ≤ 111 MPa 0.013 ≤ fl,a/fco ≤ 1.958 | 13 | 5.8 | 8.8 | Figure 4b | ||


4. Conclusions
Author Contributions
Conflicts of Interests
References
- Samaan, M.; Mirmiran, A.; Shahawy, M. Modeling of concrete confined by fiber composites. J. Struct. Eng. 1998, 124, 1025–1031. [Google Scholar] [CrossRef]
- Fardis, M.N.; Khalili, H. Concrete encased in fiberglass-reinforced plastic. ACI Struct. J. 1981, 78, 440–445. [Google Scholar]
- Huang, L.; Sun, X.; Yan, L.; Zhu, D. Compressive behavior of concrete confined with GFRP tubes and steel spirals. Polymers 2015, 7, 851–875. [Google Scholar] [CrossRef]
- Howie, I.; Karbhari, V.M. Effect of Materials Architecture on Strengthening Efficiency of Composite Wraps for Deteriorating Columns in the North-East. In Infrastructure: New Materials and Methods of Repair; Basham, K.D., Ed.; American Society of Civil Engineers: New York, NY, USA, 1994; pp. 199–206. [Google Scholar]
- Karbhari, V.M.; Gao, Y. Composite jacketed concrete under uniaxial compression-verification of simple design equations. J. Mater. Civ. Eng. 1997, 9, 185–193. [Google Scholar] [CrossRef]
- Watanabe, K.; Nakamura, H.; Honda, T.; Toyoshima, M.; Iso, M.; Fujimaki, T.; Kaneto, M.; Shirai, N. Confinement Effect of FRP Sheet on Strength and Ductility of Concrete Cylinders under Uniaxial Compression. In Proceedings of the 3rd International Symposium on Non-Metallic (FRP) Reinforcement for Concrete Structure, Sapporo, Japan, 14–16 October 1997; pp. 233–240.
- Rousakis, T. Experimental Investigation of Concrete Cylinders Confined by Carbon FRP Sheets, under Monotonic and Cyclic Axial Compressive Load; Chalmers University of Technology: Göteborg, Sweden, 2001; p. 87. [Google Scholar]
- Ilki, A.; Peker, O.; Karamuk, E.; Demir, C.; Kumbasar, N. FRP retrofit of low and medium strength circular and rectangular reinforced concrete columns. J. Mater. Civ. Eng. 2008, 20, 169–188. [Google Scholar] [CrossRef]
- Cui, C.; Sheikh, S.A. Experimental study of normal- and high-strength concrete confined with fiber-reinforced polymers. J. Compos. Constr. 2010, 14, 553–561. [Google Scholar] [CrossRef]
- Song, X.; Gu, X.; Li, Y.; Chen, T.; Zhang, W. Mechanical behavior of FRP-strengthened concrete columns subjected to concentric and eccentric compression loading. J. Compos. Constr. 2013, 17, 336–346. [Google Scholar] [CrossRef]
- Rochette, P.; Labossière, P. Axial testing of rectangular column models confined with composites. J. Compos. Constr. 2000, 4, 129–136. [Google Scholar] [CrossRef]
- Dai, J.G.; Bai, Y.L.; Teng, J.G. Behaviour and modeling of concrete confined with FRP composites of large deformability. J. Compos. Constr. 2011, 15, 963–973. [Google Scholar] [CrossRef]
- Campione, G.; La Mendola, L.; Monaco, A.; Valenza, A.; Fiore, V. Behavior in compression of concrete cylinders externally wrapped with basalt fibers. Compos. Part B 2015, 69, 576–586. [Google Scholar] [CrossRef]
- Bai, Y.L.; Dai, J.G.; Teng, J.G. Cyclic compressive behavior of concrete confined with large rupture strain FRP composites. J. Compos. Constr. 2014, 18, 04013025. [Google Scholar] [CrossRef]
- Ispir, M. Monotonic and cyclic compression tests on concrete confined with PET-FRP. J. Compos. Constr. 2014, 19, 04014034. [Google Scholar] [CrossRef]
- Yan, L. Plain concrete cylinders and beams externally strengthened with natural flax fabric reinforced epoxy composites. Mater. Struct. 2015. [Google Scholar] [CrossRef]
- Rousakis, T. Hybrid confinement of concrete by FRP sheets and fiber ropes under cyclic axial compressive loading. J. Compos. Constr. 2013, 17, 732–743. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Tourtouras, I.S. RC columns of square section-passive and active confinement with composite ropes. Compos. Part B 2014, 58, 573–581. [Google Scholar] [CrossRef]
- Feng, P.; Cheng, S.; Bai, Y.; Ye, L. Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression. Compos. Struct. 2015, 123, 312–324. [Google Scholar] [CrossRef]
- Vincent, T.; Ozbakkaloglu, T. Compressive behavior of prestressed high-strength concrete-filled aramid FRP tube columns: Experimental observations. J. Compos. Constr. 2015. [Google Scholar] [CrossRef]
- Pon, T.H.; Li, Y.F.; Shih, B.J.; Han, M.S.; Chu, G.D.; Chiu, Y.J. Experiments of Scale Effects on the Strength of FRP Reinforced Concrete. In Proceedings of the 4th National Conference on Structural Engineering, Taipei, China, September 1998; pp. 2133–2140.
- Miyauchi, K.; Inoue, S.; Kuroda, T.; Kobayashi, A. Strengthening effects of concrete columns with carbon fiber sheet. Trans. Jpn. Concr. Inst. 1999, 21, 143–150. [Google Scholar]
- Berthet, J.F.; Ferrier, E.; Hamelin, P. Compressive behavior of concrete externally confined by composite jackets. Part A: Experimental study. Constr. Build. Mater. 2005, 19, 223–232. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Vincent, T. Axial compressive behavior of circular high-strength concrete-filled FRP tubes. J. Compos. Constr. 2013, 18, 1–11. [Google Scholar] [CrossRef]
- Zohrevand, P.; Mirmiran, A. Behavior of ultra high-performance concrete confined by fiber-reinforced polymers. J. Mater. Civ. Eng. 2011, 23, 1727–1734. [Google Scholar] [CrossRef]
- Guler, S.; Copur, A.; Aydogan, M. Nonlinear finite element modeling of FRP-wrapped UHPC columns. Comput. Concr. 2013, 12, 413–429. [Google Scholar] [CrossRef]
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations in Hard Rock; Balkema, A.A., Ed.; CRC Press: Rotterdam, The Netherlands, 1995; p. 215. [Google Scholar]
- Girgin, Z.C.; Arıoglu, N.; Arıoglu, E. Evaluation of strength criteria for very-high-strength concretes under triaxial compression. ACI Struct. J. 2007, 104, 278–284. [Google Scholar]
- Girgin, Z.C. A modified failure criterion to predict ultimate strength of circular columns confined by different materials. ACI Struct. J. 2009, 106, 800–809. [Google Scholar]
- Lam, L.; Teng, J.G. Design-oriented stress-strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Benzaid, R.; Mesbah, H.; Chikh, N. FRP-confined concrete cylinders: Axial compression experiments and strength model. J. Reinf. Plast. Compos. 2010, 29, 2469–2488. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.C. Axial compressive behavior of FRP-confined concrete: Experimental test database and a new design-oriented model. Compos. Part B 2013, 55, 607–634. [Google Scholar] [CrossRef] [Green Version]
- Spoelstra, M.R.; Monti, G. FRP-confined concrete model. J. Compos. Constr. 1999, 3, 143–150. [Google Scholar] [CrossRef]
- Pessiki, S.; Harries, K.A.; Kestner, J.; Sause, R.; Ricles, J.M. The axial behavior of concrete confined with fiber reinforced composite jackets. J. Compos. Constr. 2001, 5, 237–245. [Google Scholar] [CrossRef]
- Vincent, T.; Ozbakkaloglu, T. Influence of concrete strength and confinement method on axial compressive behavior of FRP confined high- and ultra-high-strength concrete. Compos. Part B 2013, 50, 413–428. [Google Scholar] [CrossRef]
- Richart, E.; Brandtzaeg, A.; Brown, R.L. Failure of Plain and Spirally Reinforced Concrete in Compression; University of Illinois, Engineering Experimental Station: Champaign, IL, USA, 1929; Volume 190. [Google Scholar]
- Mander, J.B.; Priestley, J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Saadatmanesh, H.; Ehsani, M.R.; Li, M.W. Strength and ductility of concrete columns externally reinforced with fiber composite straps. ACI Struct. J. 1994, 91, 434–447. [Google Scholar]
- Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; ACI 440.2R-08; American Concrete Institute (ACI) Committee: Farmington Hills, MI, USA, 2008.
- Kono, S.; Inazuni, M.; Kaku, T. Evaluation of Confining Effects of CFRP Sheets on Reinforced Concrete Members. In Proceedings of the 2nd International Conference on Composites in Infrastructure, Tucson, AZ, USA, 5–7 January 1998.
- Saafi, M.; Toutanji, H.A.; Li, Z. Behaviour of concrete columns confined with fiber reinforced polymer tubes. ACI Mater. J. 1999, 96, 500–509. [Google Scholar]
- Xiao, Y.; Wu, H. Compressive behavior of concrete confined by carbon fiber composite jackets. J. Mater. Civ. Eng. 2000, 12, 139–146. [Google Scholar] [CrossRef]
- Toutanji, H.A. Stress-strain characteristics of concrete columns externally confined with advanced fibre composite sheets. ACI Mater. J. 1999, 96, 397–402. [Google Scholar]
- Teng, J.; Jiang, T.; Lam, L.; Luo, Y. Refinement of a design-oriented stress–strain model for FRP-confined concrete. J. Compos. Constr. 2009, 13, 269–278. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Rakitzis, T.D.; Karabinis, A.I. Design-oriented strength model for FRP-confined concrete members. J. Compos. Constr. 2012, 16, 615–625. [Google Scholar] [CrossRef]
- Rousakis, T.; Rakitzis, T.; Karabinis, A. Empirical Modelling of Failure Strains of Uniformly FRP Confined Concrete Columns. In Proceedings of the 6th International Conference on FRP Composites in Civil Engineering (CICE), Rome, Italy, 13–15 June 2012.
- Johnston, I.W. Comparison of two strength crieria for intact rock. J. Geotech. Eng. Div. 1985, 111, 1449–1454. [Google Scholar] [CrossRef]
- Girgin, Z.C. Modified Johnston failure criterion from rock mechanics to predict the ultimate strength of fiber reinforced polymer (FRP) confined columns. Polymers 2014, 6, 59–75. [Google Scholar] [CrossRef]
- Mirmiran, A.; Shahawy, M. Behavior of concrete columns confined by fiber composites. J. Struct. Eng. 1997, 123, 583–590. [Google Scholar] [CrossRef]
- Thériault, M.; Neale, K.W. Design equations for axially loaded reinforced concrete columns strengthened with FRP wraps. Can. J. Civ. Eng. 2000, 27, 1011–1020. [Google Scholar] [CrossRef]
- Karabinis, A.I.; Rousakis, T.C. Concrete confined by FRP material: A plasticity approach. Eng. Struct. 2002, 24, 923–932. [Google Scholar] [CrossRef]
- Lin, C.; Li, Y. An effective peak stress formula for concrete confined with carbon fibre reinforced plastics. Can. J. Civ. Eng. 2003, 30, 882–889. [Google Scholar] [CrossRef]
- Lin, H.L.; Liao, C.I. Compressive strength of reinforced concrete-column confined by composite materials. Compos. Struct. 2004, 65, 239–250. [Google Scholar] [CrossRef]
- Thériault, M.; Neale, K.W.; Claude, S. Fiber-reinforced polymer-confined circular concrete columns: Investigation of size and slenderness effects. J. Compos. Constr. 2004, 8, 323–331. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Ultimate condition of FRP-confined concrete. J. Compos. Constr. 2004, 8, 539–548. [Google Scholar] [CrossRef]
- El Chabib, H.; Nehdi, M.; El Naggar, M.H. Behavior of SCC confined in short GFRP tubes. Cem. Concr. Compos. 2005, 27, 55–64. [Google Scholar] [CrossRef]
- Mandal, S.; Hoskin, A.; Fam, A. Influence of concrete strength on confinement effectiveness of fiber-reinforced polymer circular jackets. ACI Struct. J. 2005, 102, 383–392. [Google Scholar]
- Triantafillou, T.C.; Papanicolaou, C.G.; Zissimopoulos, P.; Laourdekis, T. Concrete confinement with textile-reinforced mortar jackets. ACI Struct. J. 2006, 103, 28–37. [Google Scholar]
- Almussalam, T.H. Behavior of normal and high-strength concrete cylinders confined with E-glass/epoxy composite laminates. Compos. Part B 2007, 38, 629–639. [Google Scholar] [CrossRef]
- Jiang, T.; Teng, J.G. Analysis-oriented stress-strain models for FRP-confined concrete. Eng. Struct. 2007, 29, 2968–2986. [Google Scholar] [CrossRef]
- Wang, L.M.; Wu, Y.F. Effect of corner radius on the performance of CFRP-confined square concrete columns: Test. Eng. Struct. 2008, 30, 493–505. [Google Scholar] [CrossRef]
- Harries, K.A.; Kharel, G. Behavior and modeling of concrete subject to variable confining pressure. ACI Mater. J. 2002, 99, 180–189. [Google Scholar]
- Youssef, M.N.; Feng, M.Q.; Mosallam, A.S. Stress–strain model for concrete confined by FRP composites. Compos. B Eng. 2007, 38, 614–628. [Google Scholar] [CrossRef]
- Chikh, N.; Benzaid, R.; Mesbah, H. An experimental investigation of circular RC columns with various slenderness confined with CFRP sheets. Arab J. Sci. Eng. 2012, 37, 315–323. [Google Scholar] [CrossRef]
- Building Code Requirements for Structural Concrete (ACI Committee 318) and Commentary; American Concrete Institute Committee: Farmington Hills, MI, USA, 2008; p. 520.
- Report on High-Strength Concrete; ACI 363R-10; American Concrete Institute Committee: Farmington Hills, MI, USA, 2010; p. 65.
- Ahmad, S.M.; Shah, S.P. Stress-strain curves of concrete confined by spiral reinforcement. ACI J. Proc. 1982, 79, 484–490. [Google Scholar]
- Mesbah, H.A.; Lachemi, M.; Aïtcin, P.C. Determination of elastic properties of high-performance concrete at early ages. ACI Mater. J. 2002, 99, 37–41. [Google Scholar]
- Noguchi, T.; Tomosawa, F.; Nemati, K.M.; Chiaia, B.M.; Fantilli, A.P. A practical equation for elastic modulus of concrete. ACI Struct. J. 2009, 106, 690–696. [Google Scholar]
- Fib Model Code for Concrete Structures (fib MC2010); Ernst & Sohn Publishing: Lausanne, Switzerland, 2013; p. 434.
- Magureanu, C.; Sosa, I.; Negrutiu, C.; Heghes, B. Mechanical properties and durability of ultra-high performance concrete. ACI Mater. J. 2012, 109, 177–184. [Google Scholar]
- Designers’ Guide to EN1994-1-1. Eurocode 4: Design of composite steel and concrete structures. Part 1.1: General Rules and Rules for Buildings; British Standards Institution: London, UK, 2004.
- De Lorenzis, L.; Tepfers, R. Comparative study of models on confinement of concrete cylinders with fiber-reinforced polymer composites. J. Compos. Constr. 2003, 7, 219–237. [Google Scholar] [CrossRef]
- Girgin, Z.C.; (Yildiz Technical University, Istanbul, Turkey); Monti, G.; (Sapienza University of Rome, Rome, Italy). Personal communication, 2015.
- Nisticò, N.; Pallini, F.; Rousakis, T.; Wu, Y.F.; Karabinis, A. Peak strength and ultimate strain prediction for FRP confined square and circular concrete sections. Compos. Part B 2014, 67, 543–554. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Girgin, Z.C.; Girgin, K. A Design-Oriented Combined Model (7 MPa to 190 MPa) for FRP-Confined Circular Short Columns. Polymers 2015, 7, 1905-1917. https://doi.org/10.3390/polym7101489
Girgin ZC, Girgin K. A Design-Oriented Combined Model (7 MPa to 190 MPa) for FRP-Confined Circular Short Columns. Polymers. 2015; 7(10):1905-1917. https://doi.org/10.3390/polym7101489
Chicago/Turabian StyleGirgin, Zehra Canan, and Konuralp Girgin. 2015. "A Design-Oriented Combined Model (7 MPa to 190 MPa) for FRP-Confined Circular Short Columns" Polymers 7, no. 10: 1905-1917. https://doi.org/10.3390/polym7101489
APA StyleGirgin, Z. C., & Girgin, K. (2015). A Design-Oriented Combined Model (7 MPa to 190 MPa) for FRP-Confined Circular Short Columns. Polymers, 7(10), 1905-1917. https://doi.org/10.3390/polym7101489