Tailoring the Static and Dynamic Mechanical Properties of Tri-Block Copolymers through Molecular Dynamics Simulation
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
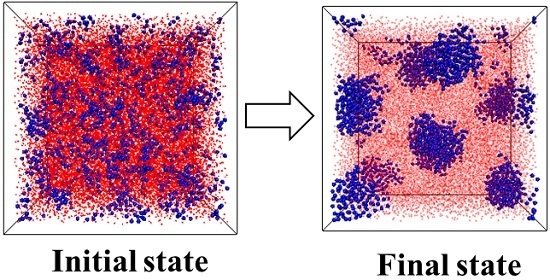
3.1. Effect of the Structural Evolution of the ABA Tri-Block Copolymer
3.2. Effect of the Temperature
3.3. Effect of the Dynamic Shear Flow
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fu, B.X.; Lee, A.; Haddad, T.S. Styrene–butadiene–styrene triblock copolymers modified with polyhedral oligomeric silsesquioxanes. Macromolecules 2004, 37, 5211–5218. [Google Scholar] [CrossRef]
- Watanabe, H.; Sato, T.; Osaki, K. Concentration dependence of loop fraction in styrene–isoprene–styrene triblock copolymer solutions and corresponding changes in equilibrium elasticity. Macromolecules 2000, 33, 2545–2550. [Google Scholar] [CrossRef]
- Aoyagi, T.; Honda, T.; Doi, M. Microstructural study of mechanical properties of the ABA triblock copolymer using self-consistent field and molecular dynamics. J. Chem. Phys. 2002, 117, 8153–8161. [Google Scholar] [CrossRef]
- Segalman, R.A.; Yokoyama, H.; Kramer, E.J. Graphoepitaxy of spherical domain block copolymer films. Adv. Mater. 2001, 13, 1152–1155. [Google Scholar] [CrossRef]
- Xiang, H.; Shin, K.; Kim, T.; Moon, S.I.; McCarthy, T.J.; Russell, T.P. Block copolymers under cylindrical confinement. Macromolecules 2004, 37, 5660–5664. [Google Scholar] [CrossRef]
- Hajduk, D.A.; Harper, P.E.; Gruner, S.M.; Honeker, C.C.; Kim, G.; Thomas, E.L.; Fetters, L.J. The gyroid: A new equilibrium morphology in weakly segregated diblock copolymers. Macromolecules 1994, 27, 4063–4075. [Google Scholar] [CrossRef]
- Zipfel, J.; Berghausen, J.; Schmidt, G.; Lindner, P.; Alexandridis, P.; Tsianou, M.; Richtering, W. Shear induced structures in lamellar phases of amphiphilic block copolymers. Phys. Chem. Chem. Phys. 1999, 1, 3905–3910. [Google Scholar] [CrossRef]
- Balmbra, R.; Clunie, J.; Goodman, J. Cubic mesomorphic phases. Nature 1969, 222, 1159–1160. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Mitchell, D.J.; Ninham, B.W. Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1976, 72, 1525–1568. [Google Scholar] [CrossRef]
- Rodríguez-Hernández, J.; Lecommandoux, S. Reversible inside-out micellization of pH-responsive and water-soluble vesicles based on polypeptide diblock copolymers. J. Am. Chem. Soc. 2005, 127, 2026–2027. [Google Scholar] [CrossRef] [PubMed]
- Schott, H. Hydrophile-lipophile balance and cloud points of nonionic surfactants. J. Pharm. Sci. 1969, 58, 1443–1449. [Google Scholar] [CrossRef] [PubMed]
- Cohen, Y.; Albalak, R.J.; Dair, B.J.; Capel, M.S.; Thomas, E.L. Deformation of oriented lamellar block copolymer films. Macromolecules 2000, 33, 6502–6516. [Google Scholar] [CrossRef]
- Makke, A.; Lame, O.; Perez, M.; Barrat, J.-L. Influence of tie and loop molecules on the mechanical properties of lamellar block copolymers. Macromolecules 2012, 45, 8445–8452. [Google Scholar] [CrossRef]
- Qi, H.; Boyce, M. Stress–strain behavior of thermoplastic polyurethanes. Mech. Mater. 2005, 37, 817–839. [Google Scholar] [CrossRef]
- Sarva, S.S.; Deschanel, S.; Boyce, M.C.; Chen, W. Stress-strain behavior of a polyurea and a polyurethane from low to high strain rates. Polymer 2007, 48, 2208–2213. [Google Scholar] [CrossRef]
- Wang, Y.; Mattice, W.L.; Napper, D.H. Simulation of the self-assembly of symmetric triblock copolymers in dilute solution. Macromolecules 1992, 25, 4073–4077. [Google Scholar] [CrossRef]
- Chen, J.-Z.; Sun, Z.-Y.; Zhang, C.-X.; An, L.-J.; Tong, Z. Self-assembly of rod–coil–rod ABA-type triblock copolymers. J. Chem. Phys. 2008, 128, 074904. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.H.; Jo, W.H. A Monte Carlo simulation for the micellization of ABA-and BAB-type triblock copolymers in a selective solvent. II. Effects of the block composition. J. Chem. Phys. 2002, 117, 8565–8572. [Google Scholar] [CrossRef]
- Song, J.; Shi, T.; Li, Y.; Chen, J.; An, L. Rigidity effect on phase behavior of symmetric ABA triblock copolymers: A Monte Carlo simulation. J. Chem. Phys. 2008, 129, 054906. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Lin, S.; He, X.; Lin, J.; Jiang, T. Self-assembly behavior of ABA coil–rod–coil triblock copolymers: A Brownian dynamics simulation approach. J. Chem. Phys. 2011, 135, 014102. [Google Scholar] [CrossRef] [PubMed]
- Parker, A.J.; Rottler, J. Molecular mechanisms of plastic deformation in sphere-forming thermoplastic elastomers. Macromolecules 2015, 48, 8253–8261. [Google Scholar] [CrossRef]
- Makke, A.; Lame, O.; Perez, M.; Barrat, J.-L. Nanoscale buckling in lamellar block copolymers: A molecular dynamics simulation approach. Macromolecules 2013, 46, 7853–7864. [Google Scholar] [CrossRef]
- Chantawansri, T.L.; Sirk, T.W.; Sliozberg, Y.R. Entangled triblock copolymer gel: Morphological and mechanical properties. J. Chem. Phys. 2013, 138, 024908. [Google Scholar] [CrossRef] [PubMed]
- Chantawansri, T.L.; Sliozberg, Y.R. Computational study of the morphology and mechanical properties of dilute ABC triblock copolymers. Korea-Aust. Rheol. J. 2014, 26, 49–61. [Google Scholar] [CrossRef]
- Chantawansri, T.L.; Sirk, T.W.; Mrozek, R.; Lenhart, J.L.; Kröger, M.; Sliozberg, Y.R. The effect of polymer chain length on the mechanical properties of triblock copolymer gels. Chem. Phys. Lett. 2014, 612, 157–161. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, H.; Tian, X.; Cui, P.; Ding, X.; Ye, X. The effects of polydimethylsiloxane on transparent and hydrophobic waterborne polyurethane coatings containing polydimethylsiloxane. Phys. Chem. Chem. Phys. 2014, 16, 6787–6794. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Allen, M.; Tildesley, D. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Liu, J.; Lu, Y.L.; Tian, M.; Li, F.; Shen, J.; Gao, Y.; Zhang, L. The interesting influence of nanosprings on the viscoelasticity of elastomeric polymer materials: Simulation and experiment. Adv. Funct. Mater. 2013, 23, 1156–1163. [Google Scholar] [CrossRef]
- Rottach, D.R.; Curro, J.G.; Grest, G.S.; Thompson, A.P. Effect of strain history on stress and permanent set in cross-linking networks: A molecular dynamics study. Macromolecules 2004, 37, 5468–5473. [Google Scholar] [CrossRef]
- Rottach, D.R.; Curro, J.G.; Budzien, J.; Grest, G.S.; Svaneborg, C.; Everaers, R. Molecular dynamics simulations of polymer networks undergoing sequential cross-linking and scission reactions. Macromolecules 2007, 40, 131–139. [Google Scholar] [CrossRef]
- Tuckerman, M.E.; Mundy, C.J.; Balasubramanian, S.; Klein, M.L. Modified nonequilibrium molecular dynamics for fluid flows with energy conservation. J. Chem. Phys. 1997, 106, 5615–5621. [Google Scholar] [CrossRef]
- Tenney, C.M.; Maginn, E.J. Limitations and recommendations for the calculation of shear viscosity using reverse nonequilibrium molecular dynamics. J. Chem. Phys. 2010, 132, 014103. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Shen, J.; Liu, J.; Li, H.; Gao, Y.; Li, X.; Wu, Y.; Zhang, L. Molecular dynamics simulations of the structural, mechanical and visco-elastic properties of polymer nanocomposites filled with grafted nanoparticles. Phys. Chem. Chem. Phys. 2015, 17, 7196–7207. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, L.; Yang, Q.; Wen, S.; Zhang, L.; Zhong, C. Computational study of nanoparticle dispersion and spatial distribution in polymer matrix under oscillatory shear flow. Langmuir 2013, 29, 13932–13942. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Shen, J.; Gao, Y.; Zhou, H.; Wu, Y.; Zhang, L. Detailed simulation of the role of functionalized polymer chains on the structural, dynamic and mechanical properties of polymer nanocomposites. Soft Matter 2014, 10, 8971–8984. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University: New York, NY, USA, 2003. [Google Scholar]
- Honeker, C.C.; Thomas, E.L. Impact of morphological orientation in determining mechanical properties in triblock copolymer systems. Chem. Mater. 1996, 8, 1702–1714. [Google Scholar] [CrossRef]
- Laurer, J.; Mulling, J.; Khan, S.A.; Spontak, R.J.; Lin, J.; Bukovnik, R. Thermoplastic elastomer gels. II. Effects of composition and temperature on morphology and gel rheology. J. Polym. Sci. B Polym. Phys. 1998, 36, 2513–2523. [Google Scholar] [CrossRef]
- Neumann, C.; Loveday, D.; Abetz, V.; Stadler, R. Morphology, dynamic mechanical properties, and phase behavior of ABC-triblock copolymers with two semicompatible elastomer blocks. Macromolecules 1998, 31, 2493–2500. [Google Scholar] [CrossRef]
- Wu, H.; Tian, M.; Zhang, L.; Tian, H.; Wu, Y.; Ning, N. New understanding of microstructure formation of the rubber phase in thermoplastic vulcanizates (TPV). Soft Matter 2014, 10, 1816–1822. [Google Scholar] [CrossRef] [PubMed]
- Hickey, R.J.; Gillard, T.M.; Lodge, T.P.; Bates, F.S. Influence of composition fluctuations on the linear viscoelastic properties of symmetric diblock copolymers near the order–disorder transition. ACS Macro Lett. 2015, 4, 260–265. [Google Scholar] [CrossRef]
- Mykhaylyk, O.O.; Parnell, A.J.; Pryke, A.; Fairclough, J.P.A. Direct imaging of the orientational dynamics of block copolymer lamellar phase subjected to shear flow. Macromolecules 2012, 45, 5260–5272. [Google Scholar] [CrossRef]
- Cui, J.; Xu, J.; Zhu, Y.; Jiang, W. Shear flow controlled morphological polydispersity of amphiphilic ABA triblock copolymer vesicles. Langmuir 2013, 29, 15704–15710. [Google Scholar] [CrossRef] [PubMed]













| Pair of Beads | ε | σ | rcutoff |
|---|---|---|---|
| A-A | 1.0 | 1.0 | 2.5 |
| A-B | 1.0 | 1.0 | 1.5 |
| B-B | 1.0 | 1.0 | 21/6 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Liu, H.; Shen, J.; Liu, J.; Wu, Y.; Zhang, L. Tailoring the Static and Dynamic Mechanical Properties of Tri-Block Copolymers through Molecular Dynamics Simulation. Polymers 2016, 8, 335. https://doi.org/10.3390/polym8090335
Zheng Z, Liu H, Shen J, Liu J, Wu Y, Zhang L. Tailoring the Static and Dynamic Mechanical Properties of Tri-Block Copolymers through Molecular Dynamics Simulation. Polymers. 2016; 8(9):335. https://doi.org/10.3390/polym8090335
Chicago/Turabian StyleZheng, Zijian, Hongji Liu, Jianxiang Shen, Jun Liu, Youping Wu, and Liqun Zhang. 2016. "Tailoring the Static and Dynamic Mechanical Properties of Tri-Block Copolymers through Molecular Dynamics Simulation" Polymers 8, no. 9: 335. https://doi.org/10.3390/polym8090335
APA StyleZheng, Z., Liu, H., Shen, J., Liu, J., Wu, Y., & Zhang, L. (2016). Tailoring the Static and Dynamic Mechanical Properties of Tri-Block Copolymers through Molecular Dynamics Simulation. Polymers, 8(9), 335. https://doi.org/10.3390/polym8090335