Drag Reduction Using Polysaccharides in a Taylor–Couette Flow
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Preparation of Polysaccharide Solution
2.3. Preparation of CNC, Surfactant and CNC-Surfactant Solution
2.4. Characterization of Additives
3. Results and Discussion
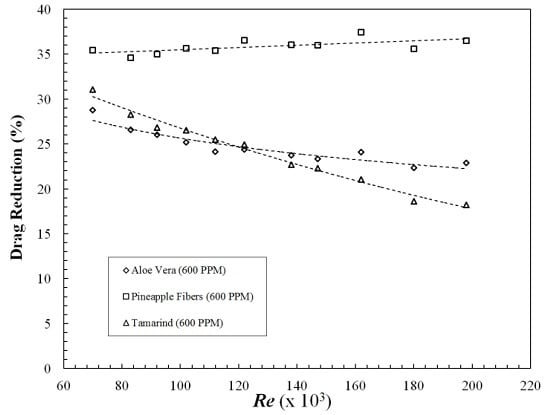
3.1. Drag Reduction Using Polysaccharides
3.2. Drag Reduction Using CNC, Surfactant and CNC-Surfactant
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bismarck, A.; Chen, L.; Griffin, J.M.; Hewitt, G.F.; Vassilicos, J.C. Heat Exchanger Design Updates; Begell House, Inc.: Redding, CT, USA, 2008. [Google Scholar]
- Ptasinski, P.K.; Nieuwstadt, F.T.M.; Van Den Brule, B.H.A.A.; Hulsen, M.A. Experiments in Turbulent Pipe Flow with Polymer Additives at Maximum Drag Reduction. Flow Turbul. Combust. 2001, 66, 159–182. [Google Scholar] [CrossRef]
- Shin, H. Reduction of Drag in Turbulence by Dilute Polymer Solutions. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1965. [Google Scholar]
- Virk, P.S.; Merrill, E.W. Viscous Drag Reduction SE-5; Wells, C.S., Ed.; Springer: Boston, MA, USA, 1969; pp. 107–130. [Google Scholar]
- Virk, P.S.; Wagger, D.L. Structure of Turbulence and Drag Reduction SE-17; Gyr, A., Ed.; Springer: Berlin/Heidelberg, Germany, 1990; pp. 201–213. [Google Scholar]
- Lumley, J.L. Drag Reduction by Additives. Annu. Rev. Fluid Mech. 1969, 1, 367–384. [Google Scholar] [CrossRef]
- Lumley, J.L. Drag reduction in turbulent flow by polymer additives. J. Polym. Sci. Macromol. Rev. 1973, 7, 263–290. [Google Scholar] [CrossRef]
- Zakin, J.L.; Lu, B.; Bewersdorff, H.-W. Surfactant Drag Reduction. Rev. Chem. Eng. 1998, 14, 1–5. [Google Scholar] [CrossRef]
- Zakin, J.L.; Chiang, J.L. Non-ionic Surfactants as Drag Reducing Addiitives. Nat. Phys. Sci. 1972, 239, 110–112. [Google Scholar] [CrossRef]
- Hoyt, J.W. Effect of additives on fluid friction. J. Basic Eng. 1972, 94, 258–285. [Google Scholar] [CrossRef]
- Patterson, G.K.; Zakin, J.L.; Rodriguez, J.M. Drag reduction: Polymer solutions, soap solutions and solid particle suspensions in pipe flow. Ind. Eng. Chem. 1969, 61, 22–30. [Google Scholar] [CrossRef]
- Hong, C.H.; Zhang, K.; Choi, H.J.; Yoon, S.M. Mechanical degradation of polysaccharide guar gum under turbulent flow. J. Ind. Eng. Chem. 2010, 16, 178–180. [Google Scholar] [CrossRef]
- Abdulbari, H.A.; Shabirin, A.; Abdurrahman, H.N. Bio-polymers for improving liquid flow in pipelines—A review and future work opportunities. J. Ind. Eng. Chem. 2013, 20, 1157–1170. [Google Scholar] [CrossRef]
- Singh, R.; Rao, S.N. Biological Control of Aphis gossypii Glover on Cucurbits by a Parasitic Wasp Trioxys indicus Subba Rao & Sharma. Biol. Agric. Hortic. 1995, 12, 227–236. [Google Scholar]
- Abdulbari, H.; Kamarulizam, N.; Nour, A.H. Grafted natural polymer as new drag reducing agent: An experimental approach. Chem. Ind. Chem. Eng. Q. 2012, 18, 361–371. [Google Scholar] [CrossRef] [Green Version]
- Peng, B.L.; Dhar, N.; Liu, H.L.; Tam, K.C. Chemistry and applications of nanocrystalline cellulose and its derivatives: A nanotechnology perspective. Can. J. Chem. Eng. 2011, 89, 1191–1206. [Google Scholar] [CrossRef]
- Greidanus, A.J.; Delfos, R.; Westerweel, J. Drag reduction by surface treatment in turbulent Taylor-Couette flow. J. Phys. Conf. Ser. 2011, 318, 82016. [Google Scholar] [CrossRef]
- Bhambri, P.; Fleck, B. Drag Reduction using high molecular weight polymers in Taylor-Couette Flow. Int. J. Mech. Prod. Eng. Res. Dev. 2016, 6, 59–72. [Google Scholar]
- Bhambri, P.; Narain, R.; Fleck, B. Thermo-responsive polymers for drag reduction in turbulent Taylor–Couette flow. Appl. Polym. Sci. 2016, 133, 44191. [Google Scholar] [CrossRef]
- Koeltzsch, K.; Qi, Y.; Brodkey, R.S.; Zakin, J.L. Drag reduction using surfactants in a rotating cylinder geometry. Exp. Fluids 2003, 34, 515–530. [Google Scholar] [CrossRef]
- Srinivasan, S.; Kleingartner, J.A.; Gilbert, J.B.; Cohen, R.E.; Milne, A.J.B.; McKinley, G.H. Sustainable drag reduction in turbulent taylor-couette flows by depositing sprayable superhydrophobic surfaces. Phys. Rev. Lett. 2015, 114, 14501. [Google Scholar] [CrossRef] [PubMed]
- Lathrop, D.P.; Fineberg, J.; Swinney, H.L. Turbulent flow between concentric rotating cylinders at large Reynolds number. Phys. Rev. Lett. 1992, 68, 1515–1518. [Google Scholar] [CrossRef] [PubMed]
- Kaboorani, A.; Riedl, B. Surface modification of cellulose nanocrystals (CNC) by a cationic surfactant. Ind. Crop. Prod. 2015, 65, 45–55. [Google Scholar] [CrossRef]
- Campolo, M.; Simeoni, M.; Lapasin, R.; Soldati, A. Turbulent Drag Reduction by Biopolymers in Large Scale Pipes. J. Fluids Eng. 2015, 137, 41102. [Google Scholar] [CrossRef]
- AbdulBari, H.A.; Letchmanan, K.; Yunus, R.M. Drag reduction characteristics using aloe vera natural mucilage: An experiment study. J. Appl. Sci. 2011, 11, 1039–1043. [Google Scholar]
- Virk, P.S. Drag reduction in rough pipes. J. Fluid Mech. 1971, 45, 225–246. [Google Scholar] [CrossRef]
- Vaseleski, R.C.; Metzner, B. Drag Reduction in the Turbulent Flow of Fiber Suspensions. AIChE J. 1974, 20, 301–306. [Google Scholar] [CrossRef]
- Zhang, Y.; Schmidt, J.; Talmon, Y.; Zakin, J.L. Co-solvent effects on drag reduction, rheological properties and micelle microstructures of cationic surfactants. J. Colloid Interface Sci. 2005, 286, 696–709. [Google Scholar] [CrossRef] [PubMed]









| Polysaccharides | Power Law Expression |
|---|---|
| Aloe Vera | τ = 0.0011 γ |
| Tamarind Powder | τ = 0.0016 γ0.9649 |
| Pineapple fiber | τ = 0.0037 γ0.8307 |
| CNC | τ = 0.0013 γ |
| CNC-Surfactant | τ = 0.0011 γ |
| Surfactant | τ = 0.0010 γ |
| Additive | Effective Diameter (nm) | Standard Deviation (nm) |
|---|---|---|
| Tamarind | 2466 | 414 |
| CNC | 736 | 24 |
| CNC-Surfactant | 1877 | 300 |
| Surfactant | 214 | 45 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhambri, P.; Narain, R.; Fleck, B. Drag Reduction Using Polysaccharides in a Taylor–Couette Flow. Polymers 2017, 9, 683. https://doi.org/10.3390/polym9120683
Bhambri P, Narain R, Fleck B. Drag Reduction Using Polysaccharides in a Taylor–Couette Flow. Polymers. 2017; 9(12):683. https://doi.org/10.3390/polym9120683
Chicago/Turabian StyleBhambri, Pallavi, Ravin Narain, and Brian Fleck. 2017. "Drag Reduction Using Polysaccharides in a Taylor–Couette Flow" Polymers 9, no. 12: 683. https://doi.org/10.3390/polym9120683
APA StyleBhambri, P., Narain, R., & Fleck, B. (2017). Drag Reduction Using Polysaccharides in a Taylor–Couette Flow. Polymers, 9(12), 683. https://doi.org/10.3390/polym9120683