Multi-Scale Simulation of Wind Farm Performance during a Frontal Passage
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Case Study and Observations
2. Methods
2.1. Computational Setup
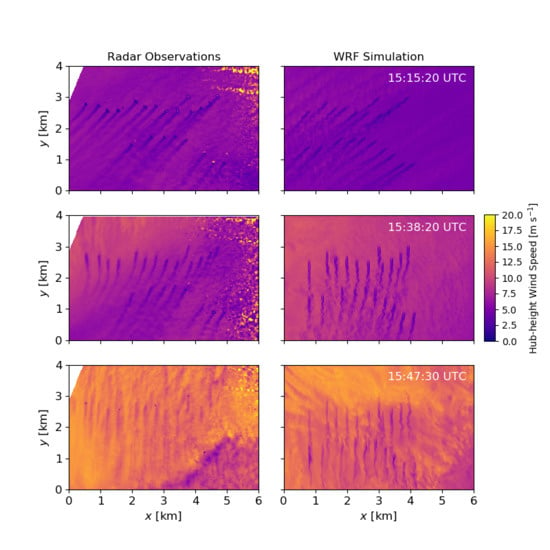
2.2. Model Validation
2.3. Model Improvements
2.3.1. Turbine Yawing
2.3.2. Turbine Power Calculation
3. Results
3.1. Background Flow and Turbine Wake Comparison
3.2. Turbulence Downscaling
3.3. Turbine Power Output Comparison
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ABL | Atmospheric boundary layer |
| AGL | Above ground level |
| ASL | Above sea level |
| CFD | Computational fluid dynamics |
| CPM | Cell perturbation method |
| GAD | Generalized actuator disk |
| GFS | Global forecast system |
| LES | Large-eddy simulation |
| MYJ | Mellor–Yamada–Janjić |
| NAM | North American Mesoscale |
| NCEP | National Centers for Environmental Prediction |
| PBL | Planetary boundary layer |
| TKE | Turbulence kinetic energy |
| UTC | Coordinated universal time |
| WRF | Weather Research and Forecasting |
References
- Högström, U.; Asimakopoulos, D.N.; Kambezidis, H.; Helmis, C.G.; Smedman, A. A field study of the wake behind a 2 MW wind turbine. Atmos. Environ. 1988, 22, 803–820. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Pryor, S.C.; Frandsen, S.T.; Hansen, K.S.; Schepers, J.G.; Rados, K.; Schlez, W.; Neubert, A.; Jensen, L.E.; Neckelmann, S. Quantifying the impact of wind turbine wakes on power output at offshore wind farms. J. Atmos. Ocean. Tech. 2010, 27, 1302–1317. [Google Scholar] [CrossRef]
- Magnusson, M.; Smedman, A.S. Air flow behind wind turbines. J. Wind. Eng. Ind. Aerod. 1999, 80, 169–189. [Google Scholar] [CrossRef]
- Thomsen, K.; Sørensen, P. Fatigue loads for wind turbines operating in wakes. J. Wind. Eng. Ind. Aerod. 1999, 80, 121–136. [Google Scholar] [CrossRef]
- Kelley, N.D.; Jonkman, B.J.; Scott, G.N.; Bialasiewicz, J.T.; Redmond, L.S. Impact of Coherent Turbulence on Wind Turbine Aeroelastic Response and Its Simulation: Preprint; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- Churchfield, M.J.; Lee, S.; Michalakes, J.; Moriarty, P.J. A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics. J. Turbul. 2012, 13, N14. [Google Scholar] [CrossRef]
- Elliott, D.L.; Barnard, J.C. Observations of wind turbine wakes and surface roughness effects on wind flow variability. Sol. Energy 1990, 45, 265–283. [Google Scholar] [CrossRef]
- Ammara, I.; Leclerc, C.; Masson, C. A viscous three-dimensional differential/actuator-disk method for the aerodynamic analysis of wind farms. J. Sol. Energ.-T. ASME 2002, 124, 345–356. [Google Scholar] [CrossRef]
- Lundquist, J.K.; DuVivier, K.K.; Kaffine, D.; Tomaszewski, J.M. Costs and consequences of wind turbine wake effects arising from uncoordinated wind energy development. Nature Energy 2019, 4, 26–34. [Google Scholar] [CrossRef]
- Pryor, S.C.; Shepherd, T.J.; Volker, P.J.H.; Hahmann, A.N.; Barthelmie, R.J. “Wind Theft” from Onshore Wind Turbine Arrays: Sensitivity to Wind Farm Parameterization and Resolution. J. Appl. Meteorol. Clim. 2020, 59, 153–174. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; Meneveau, C. Flow structure and turbulence in wind farms. Annu. Rev. Fluid Mech. 2017, 49, 311–339. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef] [Green Version]
- Meyers, J.; Meneveau, C. Optimal turbine spacing in fully developed wind farm boundary layers. Wind Energy 2012, 15, 305–317. [Google Scholar] [CrossRef] [Green Version]
- Meyers, J.; Meneveau, C. Large eddy simulations of large wind-turbine arrays in the atmospheric boundary layer. In Proceedings of the 48th AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 4–7 January 2010; p. 827. [Google Scholar]
- Calaf, M.; Parlange, M.B.; Meneveau, C. Large eddy simulation study of scalar transport in fully developed wind-turbine array boundary layers. Phys. Fluids 2011, 23, 126603. [Google Scholar] [CrossRef] [Green Version]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind. Eng. Ind. Aerod. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Chen, C.H. A numerical study of the effects of wind direction on turbine wakes and power losses in a large wind farm. Energies 2013, 6, 5297–5313. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Modeling turbine wakes and power losses within a wind farm using LES: An application to the Horns Rev offshore wind farm. Renew. Energy 2015, 75, 945–955. [Google Scholar] [CrossRef]
- Creech, A.; Früh, W.G.; Maguire, A.E. Simulations of an offshore wind farm using large-eddy simulation and a torque-controlled actuator disc model. Surv. Geophys. 2015, 36, 427–481. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, K.; Ivanell, S.; Hansen, K.S.; Mikkelsen, R.; Sørensen, J.N.; Breton, S.P.; Henningson, D. Large-eddy simulations of the Lillgrund wind farm. Wind Energy 2015, 18, 449–467. [Google Scholar] [CrossRef]
- Eriksson, O.; Lindvall, J.; Breton, S.P.; Ivanell, S. Wake downstream of the Lillgrund wind farm: A Comparison between LES using the actuator disc method and a Wind farm Parametrization in WRF. J. Phys. Conf. Ser. 2015, 625, 012028. [Google Scholar] [CrossRef]
- Abkar, M.; Sharifi, A.; Porté-Agel, F. Wake flow in a wind farm during a diurnal cycle. J. Turbul. 2016, 17, 420–441. [Google Scholar] [CrossRef]
- Guggeri, A.; Draper, M. Large-eddy Simulation of an Onshore Wind Farm with the Actuator Line Model Including Wind Turbine’s Control below and above Rated Wind Speed. Energies 2019, 12, 3508. [Google Scholar] [CrossRef] [Green Version]
- Zajaczkowski, F.J.; Haupt, S.E.; Schmehl, K.J. A preliminary study of assimilating numerical weather prediction data into computational fluid dynamics models for wind prediction. J. Wind. Eng. Ind. Aerod. 2011, 99, 320–329. [Google Scholar] [CrossRef]
- Churchfield, M.J.; Michalakes, J.; Vanderwende, B.; Lee, S.; Sprague, M.A.; Lundquist, J.K.; Moriarty, P.J. Using Mesoscale Weather Model Output as Boundary Conditions for Atmospheric Large-Eddy Simulations and Wind-Plant Aerodynamic Simulations; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2013. [Google Scholar]
- Gopalan, H.; Gundling, C.; Brown, K.; Roget, B.; Sitaraman, J.; Mirocha, J.D.; Miller, W.O. A coupled mesoscale–microscale framework for wind resource estimation and farm aerodynamics. J. Wind. Eng. Ind. Aerod. 2014, 132, 13–26. [Google Scholar] [CrossRef]
- Santoni, C.; García-Cartagena, E.J.; Ciri, U.; Zhan, L.; Valerio Iungo, G.; Leonardi, S. One-way mesoscale-microscale coupling for simulating a wind farm in North Texas: Assessment against SCADA and LiDAR data. Wind Energy 2020, 1–20. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical note NCAR/TN-475+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Fitch, A.C.; Olson, J.B.; Lundquist, J.K.; Dudhia, J.; Gupta, A.K.; Michalakes, J.; Barstad, I. Local and mesoscale impacts of wind farms as parameterized in a mesoscale NWP model. Mon. Wea. Rev. 2012, 140, 3017–3038. [Google Scholar] [CrossRef]
- Volker, P.H.J.; Badger, J.; Hahmann, A.N.; Ott, S. The Explicit Wake Parametrisation V1.0: A wind farm parametrisation in the mesoscale model WRF. Geosci. Model Dev. 2015, 8, 3715–3731. [Google Scholar] [CrossRef] [Green Version]
- Mirocha, J.D.; Kosovic, B.; Aitken, M.L.; Lundquist, J.K. Implementation of a generalized actuator disk wind turbine model into the Weather Research and Forecasting model for large-eddy simulation applications. J. Renew. Sustain. Energy 2014, 6, 013104. [Google Scholar] [CrossRef]
- Aitken, M.L.; Kosović, B.; Mirocha, J.D.; Lundquist, J.K. Large eddy simulation of wind turbine wake dynamics in the stable boundary layer using the Weather Research and Forecasting Model. J. Renew. Sustain. Energy 2014, 6, 033137. [Google Scholar] [CrossRef] [Green Version]
- Mirocha, J.D.; Rajewski, D.A.; Marjanovic, N.; Lundquist, J.K.; Kosović, B.; Draxl, C.; Churchfield, M.J. Investigating wind turbine impacts on near-wake flow using profiling lidar data and large-eddy simulations with an actuator disk model. J. Renew. Sustain. Energy 2015, 7, 043143. [Google Scholar] [CrossRef]
- Vanderwende, B.J.; Kosović, B.; Lundquist, J.K.; Mirocha, J.D. Simulating effects of a wind-turbine array using LES and RANS. J. Adv. Model. Earth Syst. 2016, 8, 1376–1390. [Google Scholar] [CrossRef]
- Marjanovic, N.; Mirocha, J.D.; Kosović, B.; Lundquist, J.K.; Chow, F.K. Implementation of a generalized actuator line model for wind turbine parameterization in the Weather Research and Forecasting model. J. Renew. Sustain. Energy 2017, 9, 063308. [Google Scholar] [CrossRef]
- Hirth, B.D.; Schroeder, J.L.; Irons, Z.; Walter, K. Dual-Doppler measurements of a wind ramp event at an Oklahoma wind plant. Wind Energy 2015, 19, 953–962. [Google Scholar] [CrossRef]
- Marjanovic, N. Simulation of the Atmospheric Boundary Layer for Wind Energy Applications. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2015. [Google Scholar]
- Muñoz-Esparza, D.; Kosović, B.; Mirocha, J.D.; van Beeck, J. Bridging the transition from mesoscale to microscale turbulence in numerical weather prediction models. Bound.-Layer Meteor. 2014, 153, 409–440. [Google Scholar] [CrossRef]
- Muñoz-Esparza, D.; Kosović, B.; Van Beeck, J.; Mirocha, J.D. A stochastic perturbation method to generate inflow turbulence in large-eddy simulation models: Application to neutrally stratified atmospheric boundary layers. Phys. Fluids 2015, 27, 035102. [Google Scholar] [CrossRef]
- Wharton, S.; Newman, J.F.; Qualley, G.; Miller, W.O. Measuring turbine inflow with vertically-profiling lidar in complex terrain. J. Wind Eng. Ind. Aerod. 2015, 142, 217–231. [Google Scholar] [CrossRef] [Green Version]
- Marjanovic, N.; Wharton, S.; Chow, F.K. Investigation of model parameters for high-resolution wind energy forecasting: Case studies over simple and complex terrain. J. Wind Eng. Ind. Aerod. 2014, 134, 10–24. [Google Scholar] [CrossRef] [Green Version]
- Wyngaard, J.C. Toward numerical modeling in the Terra Incognita. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Hutchins, N.; Marusic, I. Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 2007, 579, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Ludwig, F.L.; Chow, F.K.; Street, R.L. Effect of turbulence models and spatial resolution on resolved velocity structure and momentum fluxes in large-eddy simulations of neutral boundary layer flow. J. Appl. Meteor. Climatol. 2009, 48, 1161–1180. [Google Scholar] [CrossRef]
- Shaw, W.J.; Berg, L.K.; Cline, J.; Draxl, C.; Djalalova, I.; Grimit, E.P.; Lundquist, J.K.; Marquis, M.; McCaa, J.; Olson, J.B.; et al. The Second Wind Forecast Improvement Project (WFIP2): General Overview. Bull. Am. Meteorol. Soc. 2019, 100, 1687–1699. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Mann, J.; Palma, J.M.L.M.; Lundquist, J.K.; Barthelmie, R.J.; Belo-Pereira, M.; Brown, W.O.J.; Chow, F.K.; Gerz, T.; Hocut, C.M.; et al. The Perdigao: Peering into microscale details of mountain winds. Bull. Am. Meteorol. Soc. 2019, 100, 799–819. [Google Scholar] [CrossRef]







| Domain | [m] | Nest Ratio | [s] | Turb. Closure | Nudging | |
|---|---|---|---|---|---|---|
| d01 | 18,750 | - | 15 | MYJ | Yes | |
| d02 | 6250 | 3 | 5 | MYJ | Yes | |
| d03 | 1250 | 5 | 1 | MYJ | Yes | |
| d04 | 250 | 5 | 0.2 | MYJ | No | |
| d05 | 50 | 5 | 0.04 | TKE 1.5 | No | |
| d06 | 10 | 5 | 0.008 | TKE 1.5 | No |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arthur, R.S.; Mirocha, J.D.; Marjanovic, N.; Hirth, B.D.; Schroeder, J.L.; Wharton, S.; Chow, F.K. Multi-Scale Simulation of Wind Farm Performance during a Frontal Passage. Atmosphere 2020, 11, 245. https://doi.org/10.3390/atmos11030245
Arthur RS, Mirocha JD, Marjanovic N, Hirth BD, Schroeder JL, Wharton S, Chow FK. Multi-Scale Simulation of Wind Farm Performance during a Frontal Passage. Atmosphere. 2020; 11(3):245. https://doi.org/10.3390/atmos11030245
Chicago/Turabian StyleArthur, Robert S., Jeffrey D. Mirocha, Nikola Marjanovic, Brian D. Hirth, John L. Schroeder, Sonia Wharton, and Fotini K. Chow. 2020. "Multi-Scale Simulation of Wind Farm Performance during a Frontal Passage" Atmosphere 11, no. 3: 245. https://doi.org/10.3390/atmos11030245
APA StyleArthur, R. S., Mirocha, J. D., Marjanovic, N., Hirth, B. D., Schroeder, J. L., Wharton, S., & Chow, F. K. (2020). Multi-Scale Simulation of Wind Farm Performance during a Frontal Passage. Atmosphere, 11(3), 245. https://doi.org/10.3390/atmos11030245