Modeling Land Surface Fluxes from Uncertain Rainfall: A Case Study in the Sahel with Field-Driven Stochastic Rainfields
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Period
2.2. Generating Stochastic Rainfields
2.3. Producing LSM Simulations
2.4. Analyzing Simulation Outputs
2.4.1. Fluxes
2.4.2. Ecosystem Types
2.4.3. Aggregation Scales
2.4.4. Uncertainty Measures
2.4.5. Analysis and Presentation of Results
3. Results
3.1. Distributions and Variability of Flux Intensities
3.1.1. Distributions of Flux Ensemble Members and Means
3.1.2. Global Variance Analysis of the Simulated Flux Ensemble: Confronting Variability Sources
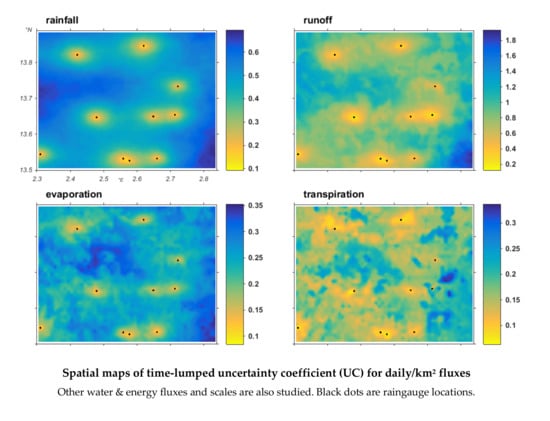
3.2. Patterns of Distributed Uncertainties
3.2.1. Distributions of Elemental Uncertainty
3.2.2. Relating Flux Uncertainty to Flux Magnitude
3.2.3. Relationship to Rainfall Uncertainty: Uncertainty Propagation Patterns
3.2.4. Effects of Ecosystem Type on Uncertainty
3.3. Scaling of Fully-Lumped Uncertainty Measures and Propagation Factors
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| αt and αxy | Power-law scaling exponents over time and space (Equation (1)), for either the standard uncertainty USD or the uncertainty coefficient UC (values in Table 3, Section 3.3, interpretation in Appendix D) |
| ACN | AMMA-CATCH-Niger |
| AMMA | African Monsoon Multidisciplinary Analyses, an international research programme |
| AMMA-CATCH | AMMA Couplage de l’Atmosphère Tropicale et du Cycle Hydrologique, a long-term field observatory (www.amma-catch.org) |
| ALMIP | AMMA land model intercomparison project (www.umr-cnrm.fr/amma-moana/amma_surf/almip) |
| Dr | Drainage below the root zone |
| Es | Direct soil evaporation |
| fully-resolved | at cell-day resolution (i.e., coarser in time that actual model computation resolution) |
| half-year | the full, 183-day study period (15 June to 14 December 2005) |
| H | Sensible heat flux |
| LC | Ecosystem/Land Cover type |
| LE | Latent heat flux |
| LSM | Land Surface Model |
| meso scale | the scale of the entire, 2530-km2 study area |
| P, Q | Rainfall, runoff |
| SEtHyS-Savannah | LSM “Suivi de l’Etat Hydrique des Sols”, version dedicated to dry savannah modelling |
| Tp | Plant transpiration |
| SPOT-HRV | High resolution visible images from the SPOT satellite system |
| UC, uncertainty coefficient | The non-dimensional uncertainty measure defined as the ratio of the standard uncertainty USD (below) to the quadratic-mean flux expectation at the same scale (see Section 2.4 and Appendix B) |
| UF, uncertainty fraction | The non-dimensional uncertainty measure defined as the ratio of the standard uncertainty USD (below) to the overall standard deviation of the entire multidimensional simulated ensemble set for the same flux type and scale (see Section 2.4 and Appendix B) |
| USD, standard uncertainty | The dimensional uncertainty measure computed as the ensemble standard deviation for the considered flux type and scale (see Section 2.4 and Appendix B) |
Appendix B
- Mixed-ecosytem flux of type f for ensemble member eat space/time location (xy,t) taken at a given space/time resolution:with a(xy,LC) the areal fraction of ecosystem LC at location xy.f (xy,t,e) = MLC (a(xy,LC)·f (xy,t,e,LC)),For (xy,t)-resolution upscaled from full resolution (cell,day):f (xy,t,e) = Mcell-to-xy; day-to-t (f (cell,day,e))
- Flux expectation: Ef (xy,t) ~ Me (f (xy,t,e))
- Uncertainty measures and associated propagation factors:
- Ufd1(d2) is the value of measure U for flux type f, taken at a given location in a subspace of dimension(s) d2, with measure-lumping over dimension(s) d1.
- Operators Md, Qd, and SDd designate the arithmetic mean, the quadratic mean, and the standard deviation, respectively, applied over the dimension(s) {d}.
Appendix C
- -
- The simulation period displays the typical annual dynamics of the Sahelian climate, with a ~four-month monsoon season followed by a long, completely dry season (until the first 2006 rainfall, in May, although only represented up to mid-December).
- -
- Superimposed onto the general two-season annual cycle, the wet season profile is characterized by a succession of wetter and drier periods, up to a nearly monthly wavelength in rainfall. Such sub-seasonal alternations are also quite typical of the Sahelian monsoon regime.
- -
- This sub-seasonal P profile propagates quite directly in time to Q as well as to Es and LE, and even to Dr despite the diffusion. It also, albeit more mildly, affects the Tp signal by modulating the unimodal LAI seasonality (Figure 1b) but with some phase inversion relative to P. This inversion may be explained at least in part by the competition for energy with the direct soil evaporation process [22], with preemption of available energy by the latter in wetter periods at the expense of transpiration. Conversely, Tp is also less affected by dry spells as roots can draw on deeper water. The sub-seasonal P modulation propagates with considerable attenuation to H (and with general phase opposition relative to LE, due to energy balancing) and to Rn.
- -
- -
- For water fluxes (Figure 4a), cell-scale ensemble members or means for Es are all greater than those for the other rainwater-redistributing fluxes at the same location, for single or mixed land covers. The range of ensemble mesoscale Es is 225–234 mm, against 379–419 mm for P, with a ratio of 57.4% for the expected fluxes. Dr is the opposite, being lowest in all cells, with an expectation of 7.3‰ of P at mesoscale and an ensemble range of 1.9–5.0 mm (note however that Dr recedes only slowly after the study period into the dry season, meaning that the ratio would be somewhat higher over a full year period). Q and Tp have intermediate magnitudes, the latter being generally the higher except in bare soil cells; mesoscale expectations are 17.6% and 20.1% of P, with ranges of 62–83 mm and 77–83 mm, respectively. Es being substantially higher than Tp agrees with the climatological analysis by Velluet et al. [22] for this area. This overall hierarchy holds throughout the period for expected fluxes at the 11-day/mesoscale (dotted running-mean curve in Figure 2), with only Tp and Q alternating in ranking: the latter predominates during the more pronounced, first two wet spells, while the opposite occurs for the weaker last two wet spells.
- -
- Among energy fluxes at the cell/half-year scale (Figure 4b), LE is nearly everywhere higher than H, although the reverse occurs mainly—but still infrequently—for the cropland cover. Corresponding mesoscale expectations are 62% and 41% of Rn (=78.4 W·m−2), respectively.
- -
- Relative weights of overall mean water and energy balance components are remarkably similar to those obtained by Velluet et al. [22], despite the differences in domain extent (space and time), data and tools, etc.
Appendix D
References
- Niang, I.; Ruppel, O.C.; Abdrabo, M.A.; Essel, A.; Lennard, C.; Padgham, J.; Urquhart, P. Africa. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group 2 to the 5th Assessment Report of the I.P.C.C.; Barros, V.R., Field, C.B., Dokken, D.J., Mastrandrea, M.D., Mach, K.J., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1199–1265. [Google Scholar]
- De Souza, K.; Kituyi, E.; Harvey, B.; Leone, M.; Murali, K.S.; Ford, J.D. Vulnerability to climate change in three hot spots in Africa and Asia: Key issues for policy-relevant adaptation and resilience-building research. Reg. Environ. Chang. 2015, 15, 747–753. [Google Scholar] [CrossRef] [Green Version]
- Kilroy, G. A review of the biophysical impacts of climate change in three hotspot regions in Africa and Asia. Reg. Environ. Chang. 2015, 15, 771–782. [Google Scholar] [CrossRef] [Green Version]
- Lebel, T.; Cappelaere, B.; Galle, S.; Hanan, N.; Kergoat, L.; Levis, S.; Vieux, B.; Descroix, L.; Gosset, M.; Mougin, E.; et al. AMMA-CATCH studies in the Sahelian region of West-Africa: An overview. J. Hydrol. 2009, 375, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Boone, A.; de Rosnay, P.; Balsamo, G.; Beljaars, A.; Chopin, F.; Decharme, B.; Delire, C.; Ducharne, A.; Gascoin, S.; Grippa, M.; et al. The AMMA Land Surface Model Intercomparison Project (ALMIP). Bull. Am. Meteorol. Soc. 2009, 90, 1865–1880. [Google Scholar] [CrossRef]
- Cappelaere, B.; Descroix, L.; Lebel, T.; Boulain, N.; Ramier, D.; Laurent, J.P.; Favreau, G.; Boubkraoui, S.; Boucher, M.; Bouzou Moussa, I.; et al. The AMMA-CATCH experiment in the cultivated Sahelian area of south-west Niger—Investigating water cycle response to a fluctuating climate and changing environment. J. Hydrol. 2009, 375, 34–51. [Google Scholar] [CrossRef]
- Leauthaud, C.; Cappelaere, B.; Demarty, J.; Guichard, F.; Velluet, C.; Kergoat, L.; Vischel, T.; Grippa, M.; Mouhaimouni, M.; Bouzou Moussa, I.; et al. A 60-year reconstructed high-resolution local meteorological data set in Central Sahel (1950-2009): Evaluation, analysis and application to land surface modelling. Int. J. Climatol. 2017, 37, 2699–2718. [Google Scholar] [CrossRef] [Green Version]
- D’Amato, N.; Lebel, T. On the characteristics of the rainfall events in the Sahel with a view to the analysis of climatic variability. Int. J. Climatol. 1998, 18, 955–974. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [Green Version]
- Petrova, I.; Miralles, D.; van Heerwaarden, C.; Wouters, H. Relation between convective rainfall properties and antecedent soil moisture heterogeneity conditions in North Africa. Remote Sens. 2018, 10, 969. [Google Scholar] [CrossRef] [Green Version]
- Wolters, D.; van Heerwaarden, C.C.; de Arellano, J.V.G.; Cappelaere, B.; Ramier, D. Effects of soil moisture gradients on the path and the intensity of a West African squall line. Q. J. R. Meteorol. Soc. 2010, 136, 2162–2175. [Google Scholar] [CrossRef]
- Hartley, A.J.; Parker, D.J.; Garcia-Carreras, L.; Webster, S. Simulation of vegetation feedbacks on local and regional scale precipitation in West Africa. Agric. For. Meteorol. 2016, 222, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Sy, S.; De Noblet-Ducoudré, N.; Quesada, B.; Sy, I.; Dieye, A.M.; Gaye, A.T.; Sultan, B. Land-Surface Characteristics and Climate in West Africa: Models’ Biases and Impacts of Historical Anthropogenically-Induced Deforestation. Sustainability 2017, 9, 1917. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y. Impact of Land–Atmosphere Interactions on Sahel Climate; Oxford University Press: Oxford, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Van Der Wijngaart, R.; Helming, J.; Jacobs, C.; Hoek, S.; Garzon Delvaux, P.A.; Gomez y Paloma, S. Irrigation and Irrigated Agriculture Potential in the Sahel: The Case of the Niger River Basin: Prospective Review of the Potential and Constraints in a Changing Climate; Joint Research Centre (JRC): Ispra, Italy, 2019. [Google Scholar] [CrossRef]
- Redelsperger, J.L.; Thorncroft, C.D.; Diedhiou, A.; Lebel, T.; Parker, D.J.; Polcher, J. African monsoon multidisciplinary analysis—An international research project and field campaign. Bull. Am. Meteorol. Soc. 2006, 87, 1739–1746. [Google Scholar] [CrossRef] [Green Version]
- Ait Hssaine, B.; Ezzahar, J.; Jarlan, L.; Merlin, O.; Khabba, S.; Brut, A.; Er-Raki, S.; Elfarkh, J.; Cappelaere, B.; Chehbouni, G. Combining a two source energy balance model driven by MODIS and MSG-SEVIRI products with an aggregation approach to estimate turbulent fluxes over sparse and heterogeneous vegetation in Sahel region (Niger). Remote Sens. 2018, 10, 974. [Google Scholar] [CrossRef] [Green Version]
- Braud, I. Spatial variability of surface properties and estimation of surface fluxes of a savannah. Agric. For. Meteorol. 1998, 89, 15–44. [Google Scholar] [CrossRef]
- Hanan, N.P. Enhanced two-layer radiative transfer scheme for a land surface model with a discontinuous upper canopy. Agric. For. Meteorol. 2001, 109, 265–281. [Google Scholar] [CrossRef]
- Marshall, M.; Tu, K.; Funk, C.; Michaelsen, J.; Williams, P.; Williams, C.; Ardö, J.; Boucher, M.; Cappelaere, B.; Grandcourt, A.; et al. Improving operational land surface model canopy evapotranspiration in Africa using a direct remote sensing approach. Hydrol. Earth Syst. Sci. 2013, 17, 1079–1091. [Google Scholar] [CrossRef] [Green Version]
- Ridler, M.E.; Sandholt, I.; Butts, M.; Lerer, S.; Mougin, E.; Timouk, F.; Kergoat, L.; Madsen, H. Calibrating a soil-vegetation-atmosphere transfer model with remote sensing estimates of surface temperature and soil surface moisture in a semi arid environment. J. Hydrol. 2012, 436, 1–12. [Google Scholar] [CrossRef]
- Velluet, C.; Demarty, J.; Cappelaere, B.; Braud, I.; Issoufou, H.B.A.; Boulain, N.; Ramier, D.; Mainassara, I.; Charvet, G.; Boucher, M.; et al. Building a field- and model-based climatology of local water and energy cycles in the cultivated Sahel—Annual budgets and seasonality. Hydrol. Earth Syst. Sci. 2014, 18, 5001–5024. [Google Scholar] [CrossRef] [Green Version]
- Verhoef, A.; Allen, S.J. A SVAT scheme describing energy and CO2 fluxes for multi-component vegetation: Calibration and test for a Sahelian savannah. Ecol. Model. 2000, 127, 245–267. [Google Scholar] [CrossRef]
- Getirana, A.; Boone, A.; Peugeot, C.; ALMIP-2 Working Group. Streamflows over a West African basin from the ALMIP-2 model ensemble. J. Hydrometeorol. 2017, 18, 1831–1845. [Google Scholar] [CrossRef]
- Grippa, M.; Kergoat, L.; Boone, A.; Peugeot, C.; Demarty, J.; Cappelaere, B.; Gal, L.; Hiernaux, P.; Mougin, E.; Ducharne, A.; et al. Modeling surface runoff and water fluxes over contrasted soils in the pastoral Sahel: Evaluation of the ALMIP2 land surface models over the Gourma region in Mali. J. Hydrometeorol. 2017, 18, 1847–1866. [Google Scholar] [CrossRef]
- Saux-Picart, S.; Ottlé, C.; Perrier, A.; Decharme, B.; Coudert, B.; Zribi, M.; Boulain, N.; Cappelaere, B.; Ramier, D. SEtHyS_Savannah: A multiple source land surface model applied to Sahelian landscapes. Agric. For. Meteorol. 2009, 149, 1421–1432. [Google Scholar] [CrossRef]
- Saux-Picart, S.; Ottlé, C.; Decharme, B.; Andre, C.; Zribi, M.; Perrier, A.; Coudert, B.; Boulain, N.; Cappelaere, B.; Descroix, L.; et al. Water and energy budgets simulation over the AMMA-Niger super-site spatially constrained with remote sensing data. J. Hydrol. 2009, 375, 287–295. [Google Scholar] [CrossRef]
- Bahat, Y.; Grodek, T.; Lekach, J.; Morin, E. Rainfall-runoff modeling in a small hyper-arid catchment. J. Hydrol. 2009, 373, 204–217. [Google Scholar] [CrossRef]
- Ogden, F.L.; Sharif, H.O.; Senarath, S.U.S.; Smith, J.A.; Baeck, M.L.; Richardson, J.R. Hydrologic analysis of the Fort Collins, Colorado, flash flood of 1997. J. Hydrol. 2000, 228, 82–100. [Google Scholar] [CrossRef]
- Arnaud, P.; Bouvier, C.; Cisneros, L.; Dominguez, R. Influence of rainfall spatial variability on flood prediction. J. Hydrol. 2002, 260, 216–230. [Google Scholar] [CrossRef]
- Messager, C.; Gallee, H.; Brasseur, O.; Cappelaere, B.; Peugeot, C.; Seguis, L.; Vauclin, M.; Ramel, R.; Grasseau, G.; Leger, L.; et al. Influence of observed and RCM-simulated precipitation on the water discharge over the Sirba basin, Burkina Faso/Niger. Clim. Dyn. 2006, 27, 199–214. [Google Scholar] [CrossRef]
- Segond, M.L.; Wheater, H.S.; Onof, C. The significance of spatial rainfall representation for flood runoff estimation: A numerical evaluation based on the Lee catchment, UK. J. Hydrol. 2007, 347, 116–131. [Google Scholar] [CrossRef]
- Vischel, T.; Lebel, T. Assessing the water balance in the Sahel: Impact of small scale rainfall variability on runoff. Part 2: Idealized modeling of runoff sensitivity. J. Hydrol. 2007, 333, 340–355. [Google Scholar] [CrossRef]
- Zhang, A.; Shi, H.Y.; Li, T.J.; Fu, X.D. Analysis of the Influence of Rainfall Spatial Uncertainty on Hydrological Simulations Using the Bootstrap Method. Atmosphere 2018, 9, 71. [Google Scholar] [CrossRef] [Green Version]
- Maggioni, V.; Reichle, R.H.; Anagnostou, E.N. The Effect of Satellite Rainfall Error Modeling on Soil Moisture Prediction Uncertainty. J. Hydrometeorol. 2011, 12, 413–428. [Google Scholar] [CrossRef]
- Serpetzoglou, E.; Anagnostou, E.N.; Papadopoulos, A.; Nikolopoulos, E.I.; Maggioni, V. Error Propagation of Remote Sensing Rainfall Estimates in Soil Moisture Prediction from a Land Surface Model. J. Hydrometeorol. 2010, 11, 705–720. [Google Scholar] [CrossRef]
- Bormann, H. Sensitivity of a soil-vegetation-atmosphere-transfer scheme to input data resolution and data classification. J. Hydrol. 2008, 351, 154–169. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res. 2011, 47, W06526. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J.; Roads, J.O.; Willmott, C.J. Uncertainties in precipitation and their impacts on runoff estimates. J. Clim. 2004, 17, 294–304. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I. Evaluation of remote-sensing-based rainfall products through predictive capability in hydrological runoff modelling. Hydrol. Process. 2010, 24, 879–891. [Google Scholar] [CrossRef]
- Pierre, C.; Bergametti, G.; Marticorena, B.; Mougin, E.; Lebel, T.; Ali, A. Pluriannual comparisons of satellite-based rainfall products over the Sahelian belt for seasonal vegetation modeling. J. Geophys. Res.-Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Nijssen, B.; Lettenmaier, D.P. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res.-Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Hossain, F.; Gebremichael, M.; Borga, M. Understanding the Scale Relationships of Uncertainty Propagation of Satellite Rainfall through a Distributed Hydrologic Model. J. Hydrometeorol. 2010, 11, 520–532. [Google Scholar] [CrossRef]
- Vieux, B.E.; Imgarten, J.M. On the scale-dependent propagation of hydrologic uncertainty using high-resolution X-band radar rainfall estimates. Atmos. Res. 2012, 103, 96–105. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F.; Ntelekos, A.A.; Georgakakos, K.P.; Smith, J.A. Towards probabilistic forecasting of flash floods The combined effects of uncertainty in radar-rainfall and flash flood guidance. J. Hydrol. 2010, 394, 275–284. [Google Scholar] [CrossRef]
- Vischel, T.; Lebel, T.; Massuel, S.; Cappelaere, B. Conditional simulation schemes of rain fields and their application to rainfall-runoff modeling studies in the Sahel. J. Hydrol. 2009, 375, 273–286. [Google Scholar] [CrossRef]
- Galle, S.; Grippa, M.; Peugeot, C.; Bouzou Moussa, I.; Cappelaere, B.; Demarty, J.; Mougin, E.; Panthou, G.; Adjomayi, P.; Agbossou, E.K.; et al. AMMA-CATCH—A critical zone observatory in West Africa monitoring a region in transition. Vadose Zone J. 2018, 17, 180062. [Google Scholar] [CrossRef] [Green Version]
- Boulain, N.; Cappelaere, B.; Ramier, D.; Issoufou, H.B.A.; Halilou, O.; Seghieri, J.; Guillemin, F.; Oi, M.; Gignoux, J.; Timouk, F. Towards an understanding of coupled physical and biological processes in the cultivated Sahel—2. Vegetation and carbon dynamics. J. Hydrol. 2009, 375, 190–203. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.; Ramier, D.; Boulain, N.; Boubkraoui, S.; Cappelaere, B.; Descroix, L.; Mougenot, B.; Timouk, F. Combining scintillometer measurements and an aggregation scheme to estimate area-averaged latent heat flux during the AMMA experiment. J. Hydrol. 2009, 375, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, M.; Favreau, G.; Scanlon, B.R.; Seidel, J.L.; Le Coz, M.; Demarty, J.; Cappelaere, B. Long-term increase in diffuse groundwater recharge following expansion of rainfed cultivation in the Sahel, West Africa. Hydrogeol. J. 2014, 22, 1293–1305. [Google Scholar] [CrossRef]
- Lohou, F.; Kergoat, L.; Guichard, F.; Boone, A.; Cappelaere, B.; Cohard, J.M.; Demarty, J.; Galle, S.; Grippa, M.; Peugeot, C.; et al. Surface response to rain events throughout the West African monsoon. Atmos. Chem. Phys. 2014, 14, 3883–3898. [Google Scholar] [CrossRef] [Green Version]
- Pfeffer, J.; Champollion, C.; Favreau, G.; Cappelaere, B.; Hinderer, J.; Boucher, M.; Nazoumou, Y.; Oï, M.; Mouyen, M.; Henri, C.; et al. Evaluating surface and subsurface water storage variations at small time and space scales from relative gravity measurements in semi-arid Niger. Water Resour. Res. 2013, 49, 3276–3291. [Google Scholar] [CrossRef]
- Ramier, D.; Boulain, N.; Cappelaere, B.; Timouk, F.; Rabanit, M.; Lloyd, C.R.; Boubkraoui, S.; Metayer, F.; Descroix, L.; Wawrzyniak, V. Towards an understanding of coupled physical and biological processes in the cultivated Sahel—1. Energy and water. J. Hydrol. 2009, 375, 204–216. [Google Scholar] [CrossRef]
- Boone, A.; Getirana, A.; Demarty, J.; Cappelaere, B.; Galle, S.; Grippa, M.; Lebel, T.; Mougin, E.; Peugeot, C.; Vischel, T. The AMMA Land Surface Model Intercomparison Project Phase 2 (ALMIP-2). Gewex News 2009, 19, 9–10. [Google Scholar]
- Boulain, N.; Cappelaere, B.; Seguis, L.; Favreau, G.; Gignoux, J. Water balance and vegetation change in the Sahel: A case study at the watershed scale with an eco-hydrological model. J. Arid Environ. 2009, 73, 1125–1135. [Google Scholar] [CrossRef]
- Boulain, N.; Cappelaere, B.; Seguis, L.; Gignoux, J.; Peugeot, C. Hydrologic and land use impacts on vegetation growth and NPP at the watershed scale in a semi-arid environment. Reg. Environ. Chang. 2006, 6, 147–156. [Google Scholar] [CrossRef]
- Leauthaud, C.; Demarty, J.; Cappelaere, B.; Grippa, M.; Kergoat, L.; Velluet, C.; Guichard, F.; Mougin, E.; Chelbi, S.; Sultan, B. Revisiting historical climatic signals to better explore the future: Prospects of water cycle changes in Central Sahel. Proc. IAHS 2015, 371, 195–201. [Google Scholar] [CrossRef] [Green Version]
- Pellarin, T.; Laurent, J.P.; Cappelaere, B.; Decharme, B.; Descroix, L.; Ramier, D. Hydrological modelling and associated microwave emission of a semi-arid region in South-western Niger. J. Hydrol. 2009, 375, 262–272. [Google Scholar] [CrossRef]
- Massuel, S.; Cappelaere, B.; Favreau, G.; Leduc, C.; Lebel, T.; Vischel, T. Integrated surface water-groundwater modelling in the context of increasing water reserves of a Sahelian aquifer. Hydrol. Sci. J. 2011, 56, 1242–1264. [Google Scholar] [CrossRef]
- Abdi, A.M.; Boke-Olén, N.; Tenenbaum, D.E.; Tagesson, T.; Cappelaere, B.; Ardö, J. Evaluating water controls on vegetation growth in the semi-arid Sahel using field and Earth observation data. Remote Sens. 2017, 9, 294. [Google Scholar] [CrossRef] [Green Version]
- Allies, A.; Demarty, J.; Olioso, A.; Bouzou Moussa, I.; Issoufou, H.B.-A.; Velluet, C.; Bahir, M.; Mainassara, I.; Oï, M.; Chazarin, J.P.; et al. Evapotranspiration estimation in the Sahel using a new ensemble-contextual method. Remote Sens. 2020, 12, 380. [Google Scholar] [CrossRef] [Green Version]
- Tagesson, T.; Ardo, J.; Cappelaere, B.; Kergoat, L.; Abdi, A.; Horion, S.; Fensholt, R. Modelling spatial and temporal dynamics of GPP in the Sahel from earth-observation-based photosynthetic capacity and quantum efficiency. Biogeosciences 2017, 14, 1333–1348. [Google Scholar] [CrossRef] [Green Version]
- Tanguy, M.; Baille, A.; González-Real, M.M.; Lloyd, C.; Cappelaere, B.; Kergoat, L.; Cohard, J.M. A new parameterisation scheme of ground heat flux for land surface flux retrieval from remote sensing information. J. Hydrol. 2012, 454–455, 113–122. [Google Scholar] [CrossRef] [Green Version]
- Verhoef, A.; Ottlé, C.; Cappelaere, B.; Murray, T.; Saux Picart, S.; Zribi, A.; Maignan, F.; Boulain, N.; Demarty, J.; Ramier, D. Spatio-temporal surface soil heat flux estimates from satellite data; results for the AMMA experiment, Fakara supersite. Agric. For. Meteorol. 2012, 154–155, 55–66. [Google Scholar] [CrossRef] [Green Version]
- Sultan, B.; Janicot, S. The West African Monsoon Dynamics. Part II: The “Preonset” and “Onset” of the Summer Monsoon. J. Clim. 2003, 16, 3407–3427. [Google Scholar] [CrossRef]
- Lebel, T.; Parker, D.J.; Flamant, C.; Holler, H.; Polcher, J.; Redelsperger, J.L.; Thorncroft, C.; Bock, O.; Bourles, B.; Galle, S.; et al. The AMMA field campaigns: Accomplishments and lessons learned. Atmos. Sci. Lett. 2011, 12, 123–128. [Google Scholar] [CrossRef]
- Balme, M.; Vischel, T.; Lebel, T.; Peugeot, C.; Galle, S. Assessing the water balance in the Sahel: Impact of small scale rainfall variability on runoff—Part 1: Rainfall variability analysis. J. Hydrol. 2006, 331, 336–348. [Google Scholar] [CrossRef]
- Guillot, G.; Lebel, T. Approximation of Sahelian rainfall fields with meta-Gaussian random functions—Part 2: Parameter estimation and comparison to data. Stoch. Environ. Res. Risk Assess. 1999, 13, 113–130. [Google Scholar] [CrossRef]
- Vischel, T.; Quantin, G.; Lebel, T.; Viarre, J.; Gosset, M.; Cazenave, F.; Panthou, G. Generation of High-Resolution Rain Fields in West Africa: Evaluation of Dynamic Interpolation Methods. J. Hydrometeorol. 2011, 12, 1465–1482. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J. Effect of rainfall uncertainty on the performance of physically based rainfall-runoff models. Hydrol. Process. 2019, 33, 160–173. [Google Scholar] [CrossRef] [Green Version]
- Deardorff, J.W. Efficient prediction of ground surface-temperature and moisture, with inclusion of a layer of vegetation. J. Geophys. Res.-Oceans 1978, 83, 1889–1903. [Google Scholar] [CrossRef] [Green Version]
- Ball, J.T. An Analysis of Stomatal Conductance. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1988. [Google Scholar]
- Collatz, G.J.; Ball, J.T.; Grivet, C.; Berry, J.A. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol. 1991, 54, 107–136. [Google Scholar] [CrossRef]
- Collatz, G.J.; Ribas-Carbo, M.; Berry, J.A. Coupled photosynthesis-stomatal conductance model for leaves of C4 plants. Aust. J. Plant Physiol. 1992, 19, 519–538. [Google Scholar] [CrossRef]
- Feurer, D.; Cappelaere, B.; Demarty, J.; Vischel, T.; Ottlé, C.; Solignac, P.A.; Saux-Picart, S.; Lebel, T.; Ramier, D.; Boulain, N.; et al. How can point rainfall data be best used to drive land surface models in the Sahel ? Presented at the 4th International AMMA Conference, Toulouse, France, 2–6 July 2012; pp. 471–472. [Google Scholar]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Nino, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION—Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Koster, R.D.; Suarez, M.J.; Heiser, M. Variance and predictability of precipitation at seasonal-to-interannual timescales. J. Hydrometeorol. 2000, 1, 26–46. [Google Scholar] [CrossRef]
- Yamada, T.J.; Koster, R.D.; Kanae, S.; Oki, T. Estimation of predictability with a newly derived index to quantify similarity among ensemble members. Mon. Weather Rev. 2007, 135, 2674–2687. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Peugeot, C.; Cappelaere, B.; Vieux, B.E.; Seguis, L.; Maia, A. Hydrologic process simulation of a semiarid, endoreic catchment in Sahelian West Niger. 1. Model-aided data analysis and screening. J. Hydrol. 2003, 279, 224–243. [Google Scholar] [CrossRef] [Green Version]











| Dimension | Aggregation Level | ||
|---|---|---|---|
| «Non-Aggregated» | Partially Aggregated | «Aggregated» | |
| space (xy) | cell (~1-km2) | - | meso (2530 km2) |
| time (t) | Day | 10/11 day | half-year (183 days) |
| ensemble (e) | Member | - | mean (=expectation, expected flux) |
| ecosystem type (LC) | separate ecosystem | - | mixed ecosystems (cell area-weighted average) |
| Variable | Rainfall, P | Runoff, Q | Evaporation, Es | Transpiration, Tp | Drainage, Dr | Net Radiation, Rn | Sensible Heat, H | Latent Heat, LE | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scale | c,d | m,d | c,p | c,d | m,d | c,p | c,d | m,d | c,p | c,d | m,d | c,p | c,d | m,d | c,p | c,d | m,d | c,p | c,d | m,d | c,p | c,d | m,d | c,p | |
| mbr. | 0 | 0 | 1.0 | 0 | 0 | 0 | 0 | 0 | 0.8 | 0 | 0 | 0 | 0 | 0 | 0 | −0.8 | −0.4 | 2.1 | −6.9 | −2.9 | 0.7 | 0 | 0.1 | 0.9 | |
| 121 | 41.6 | 3.5 | 82.5 | 16.4 | 1.4 | 10.8 | 7.2 | 1.7 | 3.2 | 1.4 | 1.0 | 6.6 | 0.2 | 0.4 | 6.0 | 5.3 | 3.2 | 4.3 | 2.8 | 1.5 | 12.5 | 8.2 | 2.6 | ||
| Range (mm/d) | exp. | 0 | 0 | 1.6 | 0 | 0 | 0.1 | 0 | 0.1 | 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | −0.5 | −0.4 | 2.2 | −6.1 | −2.8 | 0.9 | 0 | 0.1 | 1.2 |
| 82.9 | 33.4 | 2.6 | 32.0 | 10.6 | 1.1 | 9.8 | 6.9 | 1.6 | 2.7 | 1.2 | 0.9 | 0.7 | 0.1 | 0.1 | 5.8 | 5.2 | 3.0 | 3.6 | 2.7 | 1.4 | 11.4 | 8.0 | 2.1 | ||
| USD | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 19.6 | 3.5 | 0.3 | 15.3 | 2.3 | 0.2 | 3.3 | 0.5 | 0.1 | 1.0 | 0.1 | 0.1 | 1.0 | 0.0 | 0.1 | 1.0 | 0.1 | 0.1 | 3.0 | 0.3 | 0.1 | 3.7 | 0.5 | 0.2 | ||
| Mean (mm/d) | mbr. | 2.19 | 0.38 | 1.26 | 0.44 | 0.02 | 2.74 (78.4 W/m2) | 1.12 (31.9 W/m2) | 1.70 (48.5 W/m2) | ||||||||||||||||
| exp. | |||||||||||||||||||||||||
| USD | 1.22 | 0.33 | 0.22 | 0.42 | 0.12 | 0.11 | 0.29 | 0.07 | 0.07 | 0.06 | 0.01 | 0.03 | 0.017 | 0.004 | 0.016 | 0.11 | 0.02 | 0.04 | 0.19 | 0.04 | 0.05 | 0.34 | 0.08 | 0.09 | |
| mbr. | 2.95 | 2.39 | 0.16 | 5.73 | 3.41 | 0.50 | 1.15 | 1.04 | 0.10 | 1.03 | 0.83 | 0.39 | 3.71 | 1.38 | 1.77 | 0.53 | 0.52 | 0.07 | 0.77 | 0.63 | 0.12 | 1.03 | 0.94 | 0.12 | |
| CV | exp. | 2.61 | 2.37 | 0.12 | 4.36 | 3.29 | 0.42 | 1.09 | 1.03 | 0.09 | 1.00 | 0.83 | 0.38 | 2.35 | 1.29 | 1.13 | 0.52 | 0.52 | 0.06 | 0.71 | 0.63 | 0.11 | 0.98 | 0.93 | 0.11 |
| USD | 2.24 | 2.05 | 0.21 | 3.28 | 2.67 | 0.28 | 1.30 | 1.20 | 0.17 | 1.38 | 1.03 | 0.41 | 2.50 | 1.55 | 0.97 | 1.05 | 0.88 | 0.24 | 1.40 | 1.27 | 0.22 | 1.23 | 1.13 | 0.22 | |
| mbr. | 4.34 | 3.36 | −0.02 | 9.02 | 5.41 | 0.83 | 1.47 | 1.29 | 0.02 | 1.04 | 0.29 | −0.22 | 13.2 | 2.01 | 3.64 | −0.05 | −0.12 | −0.60 | −1.40 | −1.31 | 0.17 | 1.16 | 0.93 | 0.04 | |
| Skew. | exp. | 3.64 | 3.30 | −0.53 | 6.72 | 5.06 | 0.77 | 1.38 | 1.28 | −0.01 | 0.96 | 0.28 | −0.29 | 4.74 | 1.46 | 1.90 | −0.08 | −0.12 | −0.69 | −1.41 | −1.31 | 0.20 | 1.08 | 0.92 | −0.06 |
| USD | 2.47 | 2.14 | −0.35 | 4.38 | 3.67 | 0.44 | 2.25 | 2.16 | −0.61 | 2.44 | 1.15 | 0.22 | 5.53 | 2.21 | 1.34 | 1.61 | 1.02 | 0.20 | 2.94 | 2.60 | 0.03 | 2.11 | 2.03 | 0.04 | |
| mbr. | 26.6 | 15.9 | 2.63 | 109. | 39.1 | 3.74 | 5.12 | 4.65 | 2.82 | 3.41 | 1.74 | 2.22 | 376. | 7.21 | 22.0 | 1.80 | 1.75 | 2.49 | 8.72 | 7.68 | 2.47 | 4.22 | 3.62 | 2.58 | |
| Kurt. | exp. | 18.6 | 15.3 | 2.06 | 57.9 | 33.1 | 3.41 | 4.95 | 4.64 | 2.64 | 3.15 | 1.73 | 2.18 | 34.5 | 3.68 | 7.93 | 1.80 | 1.75 | 2.46 | 9.18 | 7.74 | 2.35 | 4.10 | 3.61 | 2.21 |
| USD | 8.73 | 6.93 | 3.04 | 24.6 | 18.6 | 3.09 | 9.51 | 9.11 | 4.00 | 11.4 | 3.67 | 2.44 | 48.9 | 7.60 | 4.48 | 5.98 | 3.62 | 2.98 | 15.3 | 11.8 | 2.84 | 8.89 | 8.53 | 3.09 | |
| Standard Uncertainty, USD | Uncertainty Coefficient, UC | |||||||
|---|---|---|---|---|---|---|---|---|
| Space (αxy) | Time (αt) | Space (αxy) | Time (αt) | |||||
| rainfall, P | −0.186 | (±0.007) | −0.507 | (±0.010) | −0.180 | (±0.012) | −0.319 | (±0.018) |
| runoff, Q | −0.186 | (±0.002) | −0.491 | (±0.002) | −0.163 | (±0.010) | −0.236 | (±0.015) |
| evaporation, Es | −0.206 | (±0.006) | −0.382 | (±0.009) | −0.204 | (±0.008) | −0.310 | (±0.012) |
| transpiration, Tp | −0.218 | (±0.007) | −0.224 | (±0.011) | −0.208 | (±0.006) | −0.172 | (±0.009) |
| drainage, Dr | −0.230 | (±0.003) | −0.140 | (±0.004) | −0.174 | (±0.001) | −0.043 | (±0.001) |
| net radiation, Rn | −0.207 | (±0.002) | −0.231 | (±0.003) | −0.207 | (±0.002) | −0.208 | (±0.003) |
| sensible heat, H | −0.207 | (±0.008) | −0.367 | (±0.012) | −0.204 | (±0.010) | −0.332 | (±0.015) |
| latent heat, LE | −0.205 | (±0.005) | −0.339 | (±0.007) | −0.203 | (±0.006) | −0.277 | (±0.009) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cappelaere, B.; Feurer, D.; Vischel, T.; Ottlé, C.; Issoufou, H.B.-A.; Saux-Picart, S.; Maïnassara, I.; Oï, M.; Chazarin, J.-P.; Barral, H.; et al. Modeling Land Surface Fluxes from Uncertain Rainfall: A Case Study in the Sahel with Field-Driven Stochastic Rainfields. Atmosphere 2020, 11, 465. https://doi.org/10.3390/atmos11050465
Cappelaere B, Feurer D, Vischel T, Ottlé C, Issoufou HB-A, Saux-Picart S, Maïnassara I, Oï M, Chazarin J-P, Barral H, et al. Modeling Land Surface Fluxes from Uncertain Rainfall: A Case Study in the Sahel with Field-Driven Stochastic Rainfields. Atmosphere. 2020; 11(5):465. https://doi.org/10.3390/atmos11050465
Chicago/Turabian StyleCappelaere, Bernard, Denis Feurer, Théo Vischel, Catherine Ottlé, Hassane Bil-Assanou Issoufou, Stéphane Saux-Picart, Ibrahim Maïnassara, Monique Oï, Jean-Philippe Chazarin, Hélène Barral, and et al. 2020. "Modeling Land Surface Fluxes from Uncertain Rainfall: A Case Study in the Sahel with Field-Driven Stochastic Rainfields" Atmosphere 11, no. 5: 465. https://doi.org/10.3390/atmos11050465
APA StyleCappelaere, B., Feurer, D., Vischel, T., Ottlé, C., Issoufou, H. B. -A., Saux-Picart, S., Maïnassara, I., Oï, M., Chazarin, J. -P., Barral, H., Coudert, B., & Demarty, J. (2020). Modeling Land Surface Fluxes from Uncertain Rainfall: A Case Study in the Sahel with Field-Driven Stochastic Rainfields. Atmosphere, 11(5), 465. https://doi.org/10.3390/atmos11050465