Thoron Gas Measurement Using Airflow-Through Scintillation Cell with Consideration of Progeny Deposition

Abstract

Accurate measurement of low-level thoron gas and high-accuracy calibration of thoron measurement devices are essential for assessing and preventing thoron radiological risks. This study aimed to develop a thoron gas measurement technique using an airflow-through scintillation cell for both low-level measurement and high-accuracy calibration. To achieve this, a compartment model was developed to estimate the influence of progeny deposition and accumulation on the wall of the scintillation cell to prevent an overestimation of thoron. A self-developed scintillation cell was utilised to implement and validate this technique. The lower detection limit and measurement uncertainty were then evaluated to assess the feasibility of the technique for low-level measurement and high-accuracy calibration. The results showed that the compartment model effectively addressed the influence of progeny deposition. The measurement technique achieved a lower detection limit below 100 Bq m⁻³ even with the coexistence of that of 100 Bq m⁻³ of radon and attained a measurement uncertainty (k = 2) below 10% when the concentration of thoron exceeded 1000 Bq m⁻³. In summary, this study developed a reliable and practical thoron gas measurement technique using an airflow-through scintillation cell with a consideration of progeny deposition, and is expected to contribute to the assessment and prevention of thoron radiological risk.

1. Introduction

As reported by the United Nations Scientific Committee on the Effects of Atomic Radiation [1], radon (²²²Rn) and thoron (²²⁰Rn) contribute to more than half of the annual effective dose among all sources of natural radiation worldwide. While the World Health Organization has confirmed radon as the second-leading cause of lung cancer after tobacco smoking [2], there are currently insufficient data on the lung cancer risk caused by thoron due to a paucity of surveys [3]. This situation can be mainly attributed to two reasons: first, the extensive low level of thoron due to its short half-life (55.6 s) and second, the difficulty in the measurement of thoron and the calibration of thoron measurement devices [1,3,4,5]. Nevertheless, exposure to even a low level of thoron can result in a considerable effective dose in the respiratory tract due to the high-dose conversion factor of thoron progeny compared to that of radon progeny [1,6]. Additionally, numerous surveys have revealed that the indoor levels of thoron and its progeny are comparable to, or even higher than, those of radon and its progeny in many regions [7,8,9,10,11,12,13]. Therefore, the radiological risk associated with thoron warrants significant attention. Consequently, thoron measurement methods, particularly those applied to low-level measurement and high-accuracy calibration, play fundamental roles in the assessment and prevention of thoron radiological risk.

Thoron measurements can be performed using various types of detectors, such as scintillation cells, ionisation chambers, semiconductor detectors, passivated implanted planar silicon (PIPS) detectors, and solid-state nuclear track detectors. Among these detectors, scintillation cells have gained widespread popularity owing to their high sensitivity and simplicity of use [14,15,16,17]. The thoron measurement methods employing scintillation cells can be classified into three types: (1) the grab-sample method initially developed by Hutter [15] and subsequently improved by others [16,17,18,19,20]; (2) the delayed-coincidence method proposed by Giffin et al. [21] and further developed by others [22,23,24,25]; and (3) the airflow-through method, which is commonly used for radon measurement but less studied for thoron measurement [26,27,28]. Although the grab-sample method and the delayed-coincidence method offer an advantage over the airflow-through method as they can distinguish between thoron and radon, this disadvantage of the airflow-through method could be overcome as further elaborated in the Discussion section. Moreover, the airflow-through method makes maximum use of the high sensitivity and simplicity of the scintillation cells, permitting it as a potentially promising option for low-level thoron measurements and high-accuracy calibrations.

During thoron measurements using scintillation cells, the progeny of thoron can accumulate on the walls of the scintillation cell due to deposition, resulting in additional alpha counts and an overestimation of thoron [29]. This phenomenon is referred to as the “progeny accumulation effect” in this paper. While the progeny accumulation effect has been addressed in the grab-sample method [29,30], research to date has not yet addressed this effect in the airflow-through method. This knowledge gap might be one of the primary reasons why this method was not commonly used for thoron measurements. A potential tool to address this problem was the compartment model. In 1972, Jacobi developed a compartment model to estimate the activity balance between ²²²Rn/²²⁰Rn and their progeny in the atmospheres of uranium and fluorspar mines [31]. Later, similar models were adapted and enhanced for indoor atmospheres [32,33]. Sakoda et al. further developed a numerical model derived from a compartment model to predict the behaviour of radon and its progeny in the airflow-through cell [34]. These studies suggest that the progeny accumulation effect in the airflow-through method could potentially be estimated and corrected using a compartment model.

This study aimed to develop a thoron gas measurement method using an airflow-through scintillation cell that accounts for the progeny accumulation effect. To achieve this, a compartment model was established to estimate the progeny accumulation effect, and a correction algorithm was derived from the model. Subsequently, a self-developed scintillation cell was used to validate and test the feasibility and accuracy of the proposed measurement method. Additionally, the performance of the airflow-through scintillation cell was compared with that of a grab-sample scintillation cell and a PIPS detector-based device in terms of their lower detection limit and measurement uncertainty. This research will promote the field of thoron gas measurement and calibration, thereby contributing to the assessment and prevention of thoron radiological risk.

2. Materials and Methods

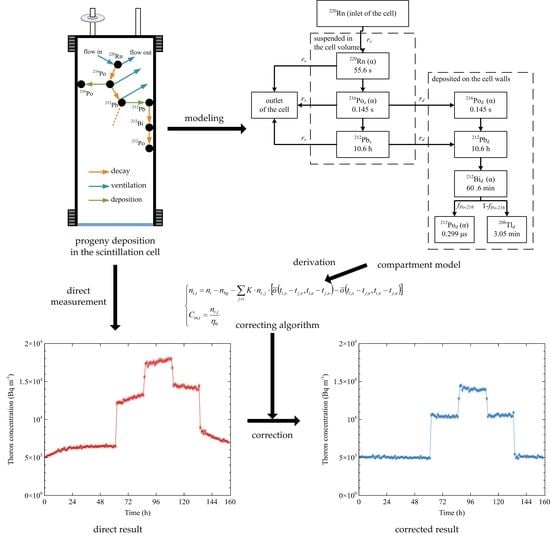
2.1. Compartment Model

In this study, a compartment model was established to evaluate the progeny accumulation effect in an airflow-through cell (Figure 1). The model consists of thoron at the inlet of the cell as the root compartment, followed by thoron and individual progeny in two states as the subsequent compartments: suspended in the cell volume and deposited on the cell walls. Transfers between the compartments involve radioactive decay, wall deposition, and ventilation due to airflow. This model simplifies the radioactive decay of suspended ²¹²Pb as it can be neglected in comparison to wall deposition and ventilation, given the extremely long half-life of ²¹²Pb (10.6 h).

The activity of thoron and its progeny in different compartments can be described by Equation (1) as a system of differential equations.

$$\left\{\begin{array}{l}\frac{d{A}_{Rn-220}}{dt}=r_v·V·C_{in}-\left({\lambda }_{Rn-220}+r_v\right)·A_{Rn-220}\\ \frac{d{A}_{Po-216,s}}{dt}={\lambda }_{Po-216}·A_{Rn-220}-\left({\lambda }_{Po-216}+r_d+r_v\right)·A_{Po-216,s}\\ \frac{d{A}_{Po-216,d}}{dt}=r_d·A_{Po-216,s}-{\lambda }_{Po-216}·A_{Po-216,d}\\ \frac{d{A}_{Pb-212,s}}{dt}={\lambda }_{Pb-212}·A_{Po-216,s}-\left(r_d+r_v\right)·A_{Pb-212,s}\\ \frac{d{A}_{Pb-212,d}}{dt}={\lambda }_{Pb-212}·A_{Po-216,d}+r_d·A_{Pb-212,s}-{\lambda }_{Pb-212}·A_{Pb-212,d}\\ \frac{d{A}_{Bi-212,d}}{dt}={\lambda }_{Bi-212}·A_{Pb-212,d}-{\lambda }_{Bi-212}·A_{Bi-212,d}\\ \frac{d{A}_{Po-212,d}}{dt}=f_{Po-212}·{\lambda }_{Po-212}·A_{Bi-212,d}-{\lambda }_{Po-212}·A_{Po-212,d}\\ \frac{d{A}_{Tl-208,d}}{dt}=\left(1-f_{Po-212}\right)·{\lambda }_{Tl-208}·A_{Bi-212,d}-{\lambda }_{Tl-208}·A_{Tl-208,d}\end{array}\right.$$

(1)

where A_x denotes the activity of thoron or its progeny (Bq), and the subscript x refers to the specific isotope and state (s for suspended in the cell volume and d for deposited on the cell walls). t denotes the measurement time (s); C_in denotes the activity concentration of thoron at the inlet of the cell (Bq m⁻³); V denotes the volume of the cell (m⁻³); r_v denotes the ventilation rate (s⁻¹); r_d denotes the deposition rate (s⁻¹); λ_i denotes the decay constant of isotope i (s⁻¹); f_Po-212 is the branching ratio of ²¹²Bi decay to ²¹²Po (dimensionless).

Under the assumption that C_in is constant, and that the activity of thoron and its progeny is equal 0 at time t = 0, Equation (2) provides an approximate analytic solution to Equation (1). In Equation (2), the change in activity over time of ²²⁰Rn, ²¹⁶Po, and suspended ²¹²Pb were omitted, as they reach the equilibrium rapidly due to the speedy ventilation rate of the cell during thoron measurement. For instance, the equilibrium time will be less than 30 s, given a common ventilation rate of 0.17 s⁻¹ (cell volume = 0.27 L; airflow rate = 2.7 L min⁻¹).

$$\left\{\begin{array}{l}{A}_{Rn-220}\left(t\right)=\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·C_{in}\\ A_{Po-216,s}\left(t\right)=\frac{{\lambda }_{Po-216}}{{\lambda }_{Po-216}+r_d+r_v}·\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·C_{in}\\ A_{Po-216,d}\left(t\right)=\frac{r_d}{{\lambda }_{Po-216}+r_d+r_v}·\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·C_{in}\\ A_{Pb-212,s}\left(t\right)=\frac{{\lambda }_{Pb-212}}{r_d+r_v}·\frac{{\lambda }_{Po-216}}{{\lambda }_{Po-216}+r_d+r_v}·\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·C_{in}\\ A_{Pb-212,d}\left(t\right)=\frac{r_d}{r_d+r_v}·\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·C_{in}·\left[1-\exp \left(-{\lambda }_{Pb-212}·t\right)\right]\\ A_{Bi-212,d}\left(t\right)=\frac{r_d}{r_d+r_v}·\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·C_{in}·o\left(t\right)\\ A_{Po-212,d}\left(t\right)=f_{Po-212}·\frac{r_d}{r_d+r_v}·\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·C_{in}·o\left(t\right)\end{array}\right.$$

(2)

where o(t) denotes a function as shown in Equation (3), which is referred to as the “normalised accumulation function” in this paper. This function is a pivotal concept in understanding the progeny accumulation effect, since it characterises the growth process of the effect over time during thoron measurement. Specifically, this function takes on a value of 0 at the start of the measurement and gradually approaches a value of 1 as time increases.

$$o\left(t\right)=1-\frac{{\lambda }_{Bi-212}}{{\lambda }_{Bi-212}-{\lambda }_{Pb-212}}·\exp \left(-{\lambda }_{Pb-212}·t\right)+\frac{{\lambda }_{Pb-212}}{{\lambda }_{Bi-212}-{\lambda }_{Pb-212}}·\exp \left(-{\lambda }_{Bi-212}·t\right)$$

(3)

The alpha counting rate recorded by the scintillation cell, n(t), consists of three components: (1) the counting rate contributed by ²²⁰Rn and ²¹⁶Po (including the suspended and deposited states), n_t; (2) the counting rate contributed by deposited ²¹²Bi and ²¹²Po, n_p, namely the counting rate resulting from the progeny accumulation effect; (3) the intrinsic background of the measurement device, n_bg. Then,

$$n\left(t\right)=n_t\left(t\right)+n_p\left(t\right)+n_{bg}$$

(4)

where n_t(t) and n_p(t) satisfy Equation (5):

$$\left\{\begin{array}{l}{n}_t\left(t\right)=A_{Rn-220}\left(t\right)·{\epsilon }_{Rn-220}+A_{Po-216,s}\left(t\right)·{\epsilon }_{Po-216,s}+A_{Po-216,d}\left(t\right)·{\epsilon }_{Po-216,d}\\ n_p\left(t\right)=A_{Bi-212-a}\left(t\right)·\left(1-f_{Po-212}\right)·{\epsilon }_{Bi-212,d}+A_{Po-212-a}\left(t\right)·{\epsilon }_{Po-212,d}\end{array}\right.$$

(5)

where ε_x represents the detection efficiency of the scintillation cell for thoron or its progeny (dimensionless), and the subscript x refers to the specific isotope and state.

Define

$$\left\{\begin{array}{l}{\eta }_0=\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·\left({\epsilon }_{Rn-220}+\frac{{\lambda }_{Po-216}}{{\lambda }_{Po-216}+r_d+r_v}·{\epsilon }_{Po-216,s}+\frac{r_d}{{\lambda }_{Po-216}+r_d+r_v}·{\epsilon }_{Po-216,d}\right)\\ {\eta }_1=\frac{r_d}{r_d+{\lambda }_v}·\frac{r_v}{{\lambda }_{Rn-220}+r_v}·V·\left[\left(1-f_{Po-212}\right)·{\epsilon }_{Bi-212,d}+f_{Po-212}·{\epsilon }_{Po-212,d}\right]\\ K=\frac{{\eta }_1}{{\eta }_0}\end{array}\right.$$

(6)

where the parameter η₀ represents the counting rate contributed by ²²⁰Rn and ²¹⁶Po due to a continuous inflow of thoron at the unit concentration; the parameter η₁ represents the counting rate resulting from the progeny accumulation effect due to the same inflow at equilibrium (i.e., when o(t) = 1); the parameter K is the ratio of η₁ to η₀, which is referred to as the “accumulation effect coefficient” in this paper. This parameter is another pivotal concept in understanding the progeny accumulation effect, along with the normalised accumulation function, as it represents the relative intensity of the progeny accumulation effect at equilibrium.

Substituting Equations (2) and (6) into Equation (5),

$$\left\{\begin{array}{l}{n}_t\left(t\right)={\eta }_0·C_{in}\\ n_p\left(t\right)=K·{\eta }_0·C_{in}·o\left(t\right)\end{array}\right.$$

(7)

Equation (7) reveals a linear relationship between the alpha counting rate, n_t(t), and the concentration of thoron in the ambient atmosphere. As a result, it is possible to indirectly measure thoron gas by calculating n_t(t) through subtracting n_p(t) and n_bg from the measured counting rate, n(t), with η₀ serving as the response factor for this method.

2.2. Calibration Procedure

A calibration procedure was designed to obtain the indispensable parameters of the airflow-through scintillation cell for thoron measurement, including the intrinsic background, n_bg, the response factor, η₀, and the accumulation effect coefficient, K. Prior to the calibration experiments, the scintillation cell was left unoccupied for a minimum of three days to avoid any contamination from either radon or thoron progeny. Subsequently, the scintillation cell was purged and filled with nitrogen, following a calibration trial to determine the intrinsic background. Finally, the scintillation cell was connected to a homemade thoron chamber with a fixed thoron concentration [35], following another calibration trial to determine the response factor for thoron gas, η₀, and the accumulation effect coefficient, K.

The response factor, η₀, and the accumulation effect coefficient, K, can be solved from the measurement result based on Equations (4) and (7). By substituting Equation (7) into Equation (4), the latter yields Equation (8), which reveals a linear relationship between the net counting rate, n_net(t), and the normalised accumulation function, o(t):

$$n_{net}\left(t\right)=n\left(t\right)-n_{bg}={\eta }_0·C_{in}+K·{\eta }_0·C_{in}·o\left(t\right)$$

(8)

By integrating it for measurement cycle i, Equation (8) can be written as

$$n_{net,i}={\eta }_0·C_{in}+K·{\eta }_0·C_{in}·\overline{o}\left(t_{i,s},t_{i,e}\right)$$

(9)

where n_net,i denotes the average net counting rate in the measurement cycle, i; t_i,s and t_i,e denote the starting time and ending time of measurement cycle i, respectively; $\overline{o}\left(t_{i,s},t_{i,e}\right)$ denotes the average value of o(t) during measurement cycle i, which could be calculated by integrating Equation (3):

$$\begin{array}{cc}\hfill \overline{o}\left(t_{i,s},t_{i,e}\right)=& 1-\frac{{\lambda }_{Bi-212}}{\left({\lambda }_{Bi-212}-{\lambda }_{Pb-212}\right)·{\lambda }_{Pb-212}·\left(t_{i,e}-t_{i,s}\right)}·\left[\exp \left(-{\lambda }_{Pb-212}·t_{i,s}\right)-\exp \left(-{\lambda }_{Pb-212}·t_{i,e}\right)\right]\hfill \\ & +\frac{{\lambda }_{Pb-212}}{\left({\lambda }_{Bi-212}-{\lambda }_{Pb-212}\right)·{\lambda }_{Bi-212}·\left(t_{i,e}-t_{i,s}\right)}·\left[\exp \left(-{\lambda }_{Bi-212}·t_{i,s}\right)-\exp \left(-{\lambda }_{Bi-212}·t_{i,e}\right)\right]\hfill \end{array}$$

(10)

A linear regression plot of the average net counting rate, n_net,i, versus the average normalised accumulation function, $\overline{o}\left(t_{i,s},t_{i,e}\right)$, will determine the intercept to be ${\eta }_0·C_{in}$ and the slope to be $K·{\eta }_0·C_{in}$. Therefore, the response factor, ${\eta }_0$, could be estimated by dividing the intercept by the known thoron concentration, C_in, and the accumulation effect coefficient, K, can be estimated by dividing the slope by the intercept.

A note of caution should be given here: the data of the first several minutes should be discarded in the linear regression, since ²²⁰Rn and ²¹⁶Po might not reach equilibrium at that time, and since there is a discrepancy between the theoretical equations and the actual situation.

2.3. Algorithm for Correcting Progeny Accumulation Effect and Estimating Thoron Concentration

To estimate the progeny accumulation effect during a measurement, the contribution of the inflow of thoron gas in each measurement cycle was separately considered. Specifically, the counting rate resulting from the progeny accumulation effect in measurement cycle i due to the inflow of thoron gas in measurement cycle j, n_p,i,j, was estimated separately using Equation (11).

$$n_{p,i,j}=K·{\eta }_0·C_{in,j}·\lfloor \overline{o}\left(t_{i,s}-t_{j,s},t_{i,e}-t_{j,s}\right)-\overline{o}\left(t_{i,s}-t_{j,e},t_{i,e}-t_{j,e}\right)\rfloor$$

(11)

where C_in,j denotes the average concentration of thoron at the inlet of the cell in measurement cycle j.

Therefore, the counting rate resulting from the progeny accumulation effect in measurement cycle i, n_p,i, was estimated using Equation (12).

$$n_{p,i}={\displaystyle \sum _{j<i}K·{\eta }_0·C_{in,j}·\left[\overline{o}\left(t_{i,s}-t_{j,s},t_{i,e}-t_{j,s}\right)-\overline{o}\left(t_{i,s}-t_{j,e},t_{i,e}-t_{j,e}\right)\right]}$$

(12)

By combining Equations (4), (7) and (12), Equation (13) is obtained, which provides a correction algorithm for the progeny accumulation effect, as well as an estimation algorithm for the thoron concentration in each measurement cycle.

$$\left\{\begin{array}{l}{n}_{t,i}=n_i-n_{bg}-{\displaystyle \sum _{j<i}K·n_{t,j}·\left[\overline{o}\left(t_{i,s}-t_{j,s},t_{i,e}-t_{j,s}\right)-\overline{o}\left(t_{i,s}-t_{j,e},t_{i,e}-t_{j,e}\right)\right]}\\ C_{in,i}=\frac{n_{t,i}}{{\eta }_0}\end{array}\right.$$

(13)

The algorithm designed to correct the progeny accumulation effect and estimate thoron concentration has been successfully implemented in a self-developed program called PAE Corrector. The application and source code are freely available for academic or learning purposes, and can be found on Github accessed on 5 May 2023 (https://codeload.github.com/zhaochao2073/PAECorrector/zip/refs/heads/main).

2.4. Laboratory Validation and Test

To verify the feasibility and accuracy of the measurement method proposed in this study, laboratory experiments were conducted in the thoron chamber at the Shanghai Institute of Measurement and Testing Technology (SIMT) [35]. The proposed method was applied using a self-developed scintillation cell [36], and the thoron concentration was simultaneously measured using a PIPS detector-based device (referred to as a “PIPS device” throughout the latter part of this article) for comparison purposes.

The thoron chamber used in the study has an inner size of 60 × 90 × 55 cm³ and a total volume of about 300 L [35]. It contains four sets of replaceable ion-exchanged solid thoron sources [37], allowing rapid switching of the activity concentration of thoron gas in the range of 1000 Bq m⁻³ to 50,000 Bq m⁻³ by changing thoron sources. Since the thoron sources contain almost no ²²⁶Ra, the radon concentration in the chamber is negligible (<1%) [36]. The thoron gas has satisfactory stability (<3%) and uniformity (<8%) within the chamber according to our previous study [36].

The scintillation cell used in this study is a cylindrical vessel (Figure 2), 53.0 mm in diameter and 122.4 mm in height (V = 270 mL), which is very similar to the scintillation cell used in several previous studies [16,18,20]. Its inner lateral wall is coated with a ZnS(Ag) scintillator to detect alpha particles. To reduce the influence of thoron decay during measurement, which was systematically discussed in our previous study [27], a relatively higher airflow rate of 2.7 L min⁻¹ was used for this scintillation cell.

The PIPS device was developed by Peking University and the State Key Laboratory of NBC Protection for Civilian. It consists of a 2000 mm² PIPS detector, a multi-channel analyser, a micro controller unit and a small cylindrical chamber with a diameter of nearly 50.2 mm and a height of nearly 11.25 mm (V = 22 mL). The device determines the activity concentration of thoron gas by detecting the alpha particles emitted from thoron and its detection efficiency was determined by Monte Carlo simulation. The airflow rate of this device is 2 L min⁻¹. Since this device also works in the airflow-through mode, the behaviour of thoron progeny in the detection chamber can be described by the proposed compartmental model. Additionally, this device can distinguish thoron and its progeny from the measured energy spectrum, allowing it to directly measure the thoron progeny. Therefore, the compartmental model could be rigorously validated by comparing the theoretical predictions with the experimental results of the counting rate contributed by thoron progeny using this device.

2.5. Evaluation of Lower Detection Limit and Measurement Uncertainty

To illustrate the comparative advantages of the airflow-through scintillation cell method in terms of its lower detection limit and measurement uncertainty, the scintillation cell and the PIPS device used in this study were selected as representative measurement devices to assess these characteristics. For the scintillation cell, both the airflow-through method and the grab-sample method were evaluated.

The lower detection limit (L_D) of a given thoron measurement device can be calculated using Equation (14) with the assumption that the risks of type I and type II errors are both 0.05 [38,39].

$$L_D=\frac{2.71+4.65\sqrt{M}}{S_{Tn}·T}$$

(14)

where S_Tn denotes the sensitivity coefficient which converts the activity concentration of thoron into the counting rate for the given device, M denotes the background counts, and T denotes the sample measurement time. In case radon coexists with thoron in general, the alpha count contributed by radon should be deducted from the total counts (as further detailed in the Discussion section) and taken into account as a component of background counts, M:

$$M=n_{bg}·T+S_{Rn}·C_{Rn}·T$$

(15)

where n_bg denotes the intrinsic background counting rate of the given device, C_Rn denotes the activity concentration of radon which interferes with thoron measurement, and S_Rn denotes the sensitivity coefficient which converts the interfering radon activity concentration into the counting rate of for the given device.

In the case of the airflow-through scintillation cell, the sensitivity coefficient, S_Tn, is simply the response factor, ${\eta }_0$:

$$S_{Tn}={\eta }_0$$

(16)

In the case of the grab-sample scintillation cell, the decay of thoron during measurement should be considered; therefore,

$$S_{Tn}=\frac{{\eta }_0·{\displaystyle {\int }_0^T\exp \left(-{\lambda }_{Rn-220}·t\right)}\mathrm{d}t}{T}$$

(17)

In the case of the PIPS device, the valued of the sensitivity coefficient, S_Tn, and the background counting rate, n_bg, were experimentally determined to be 1.07 × 10⁻³ min⁻¹ (Bq m⁻³)⁻¹ and 0.1 h⁻¹, respectively.

As regards the evaluation of measurement uncertainty, the uncertainty components contributed by the calibrated parameters (e.g., the intrinsic background, n_bg, the sensitivity coefficient, S_Tn, and the accumulation effect coefficient, K) were disregarded, since these uncertainty components can vary in practice and independent of the measurement method. Therefore, only the statistical fluctuations of the total counts, which conform to the Poisson distribution, were considered in the uncertainty evaluation.

In the case of the airflow-through scintillation cell, the deposited progeny also contributes to the total counting. However, it is impossible to determine the contribution of the deposited progeny as it is not determined by the current thoron concentration, but by the unknown historical thoron concentration and the measurement time. To overcome this difficulty, we simply assumed that the thoron concentration was constant, and that the progeny accumulation effect had reached equilibrium. With this assumption, the expanded relative uncertainty of measurement value (U_rel) was estimated according to Equation (18):

$$U_{\mathit{rel}}=k\frac{\sqrt{{\eta }_0·C_{Tn}·T+K·{\eta }_0·C_{Tn}·T+M}}{{\eta }_0·C_{Tn}·T}$$

(18)

where k is the coverage factor.

In the case of the grab-sample scintillation cell, the expanded relative uncertainty of the measurement value (U_rel) was estimated according to Equation (19) considering the decay of thoron during measurement.

$$U_{\mathit{rel}}=k\frac{\sqrt{{\eta }_0·C_{Tn}·{\displaystyle {\int }_0^T\exp \left(-{\lambda }_{Rn-220}·t\right)}\mathrm{d}t+M}}{{\eta }_0·C_{Tn}·{\displaystyle {\int }_0^T\exp \left(-{\lambda }_{Rn-220}·t\right)}\mathrm{d}t}$$

(19)

In the case of the PIPS detector, the expanded relative uncertainty of the measurement value (U_rel) of the PIPS detector method was estimated according to Equation (20).

$$U_{\mathit{rel}}=k\frac{\sqrt{S_{Tn}·C_{Tn}·T+M}}{S_{Tn}·C_{Tn}·T}$$

(20)

3. Results

3.1. Calibration Results of the Scintillation Cell

The intrinsic background of the scintillation cell was determined to be 1.02 min⁻¹ in a background calibration trial with the scintillation cell purged and filled with nitrogen. Following the background calibration trial, a calibration trial with a fixed thoron concentration of 5480 Bq was conducted. The direct measurement results (Figure 3a) depicted a growth in the net counting rate with the measurement time, despite the constant thoron concentration, thereby indicating the progeny accumulation effect. This result highlighted that the measurement results would need to be corrected for the progeny accumulation effect to ensure accuracy.

The linear regression plot of the net counting rate, n_net,i, versus the average normalised accumulation function $\overline{o}\left(t_{i,s},t_{i,e}\right)$ (Figure 3b) presented a satisfactory linear relation between them. According to the linear regression, the response factor for thoron gas, ${\eta }_0$, of the scintillation cell was determined to be 0.0236 min⁻¹ (Bq m⁻³)⁻¹, and the accumulation effect coefficient, K, of the scintillation cell was determined to be 0.314.

3.2. Validation of the Compartment Model Using PIPS Detector

A comparison of the counting rates of the ²¹²Po deposited in the PIPS device was performed between the theoretical prediction calculated by the compartment model and the experimental results obtained from the measured spectrum (Figure 4). As shown in Figure 4, the increasing trend of the theoretical prediction was consistent with the experimental results. This result presented compelling and comprehensive evidence supporting the accuracy of the compartment model in predicting the behaviour of thoron progeny within an airflow-through cell.

3.3. Laboratory Test Results

A laboratory test lasting for 160 h was conducted in the thoron chamber at SIMT, and consisted of five stages. The thoron concentration in the chamber was switched by changing the ion-exchanged solid thoron sources between the different stages of the test, and remained constant within each individual stage. Both the scintillation cell and the PIPS device were used to measure the thoron concentration, and the measurement results are shown in Figure 5.

As shown in Figure 5, the measurement results of the scintillation cell that implemented the progeny accumulation correction exhibited consistency with those obtained from the PIPS device, despite the reciprocating changes in the thoron concentration. This finding provides convincing evidence that the correction method effectively addressed the progeny accumulation effect. Conversely, Figure 5 also presents the measurement results of the scintillation cell without the progeny accumulation correction, which exhibited an obvious change during each stage with a constant thoron concentration (e.g., 0 h to 60 h), and were notably greater than the results of the PIPS device. This emphasised the significance of the progeny accumulation correction once again.

Additionally, Figure 5 demonstrates that the measurement results of the scintillation cell exhibited significantly less fluctuation than those of the PIPS device did, indicating that the measurement results of the scintillation cell were more precise. This observation will be further discussed in the subsequent section.

3.4. Comparison on Lower Detection Limit and Measurement Uncertainty

Table 1. The parameters of the airflow-through scintillation cell, the grab-sample scintillation cell, and the PIPS device.

Parameters	Airflow-Through Scintillation Cell	Grab-Sample Scintillation Cell		PIPS Device
		T = 1 min	T = 10 min
STn (min−1 (Bq m−3)−1)	2.36 × 10−2	1.94 × 10−2	3.67 × 10−3	1.07 × 10−3
SRn (min−1 (Bq m−3)−1)	2.70 × 10−2	1.17 × 10−2	1.74 × 10−2	0.85 × 10−3
nbg (min−1)	1.02	1.02	1.02	1.67 × 10−3
K *	0.314	/	/	/

* Not applicable for the grab-sample scintillation cell and the PIPS device.

provides the essential parameters of the airflow-through scintillation cell, the grab-sample scintillation cell and the PIPS device, which were utilised to evaluate their respective lower detection limit and measurement uncertainty. The parameters of the airflow-through scintillation cell and the PIPS device were determined experimentally, while the S_Tn and S_Rn of the grab-sample scintillation cell were calculated based on the detection efficiency of the scintillation cell and the law of radioactive decay [18]. For the grab-sample scintillation cell, thoron measurement times of 1 min and 10 min were chosen as representatives for evaluation purposes. The former was selected since a short thoron measurement time was commonly used in the grab-sample method limited by the short half-life of thoron, and 1 min is a typical value of this [15,18]. Meanwhile, the latter was selected to demonstrate the inconsistency of a relatively long thoron measurement time in the grab-sample method and to allow for a comparison with other techniques using the same measurement time. It can be seen from Table 1 that the sensitivity coefficient of thoron decreased by one order of magnitude with a thoron measurement time of 10 min for the grab-sample scintillation cell, highlighting the unsuitability of a long thoron measurement time. It should be noted that, the airflow-through scintillation cell was assumed to be capable of measuring thoron with the coexistence of radon, which was supported by the use of an ancillary measurement device that is sensitive only to radon, as further elaborated in the Discussion section.

Table 2. The lower detection limit (Bq m⁻³) of the airflow-through scintillation cell, the grab-sample scintillation cell, and the PIPS device.

Concentration of Radon (Bq m−3)	Airflow-Through Scintillation Cell		Grab-Sample Scintillation Cell		PIPS Device
	T = 10 min	T = 60 min	T =1 min	T = 10 min	T = 10 min	T = 60 min
0	74	28	383	478	309	65
50	107	41	444	624	542	160
100	132	51	495	739	658	207
200	167	66	580	925	823	275
1000	341	137	996	1793	1522	560

presents the lower detection limits of the airflow-through scintillation cell, the grab-sample scintillation cell, and the PIPS device. As shown in Table 2, the lower detection limits of all devices grew with the increasing concentration of coexisting radon. Moreover, the lower detection limits of the grab-sample scintillation cell decreased as the thoron measurement time increased, which is in contrast to the behaviour of the other devices. This further emphasised the unsuitability of a long thoron measurement time for the grab-sample scintillation cell. Notably, Table 2 highlights that the airflow-through scintillation cell exhibited the most outstanding lower detection limits regardless of the concentration of coexisting radon, and could attain a lower detection limit below 100 Bq m⁻³ even with the presence of that of 100 Bq m⁻³ of radon, which is an essential prerequisite for conducting low-level thoron surveys.

Table 3. The expanded relative measurement uncertainty (k = 2) of the airflow-through scintillation cell, the grab-sample scintillation cell, and the PIPS device *.

Concentration of Thoron (Bq m−3)	Concentration of Radon (Bq m−3)	Airflow-Through Scintillation Cell		Grab-Sample Scintillation Cell		PIPS Device
		T = 10 min	T = 60 min	T =1 min	T = 10 min	T = 10 min	T = 60 min
100	0	54%	22%	/	/	/	80%
100	100	/	29%	/	/	/	/
500	0	22%	9%	68%	58%	87%	35%
500	100	24%	10%	71%	/	/	38%
500	1000	35%	14%	/	/	/	/
1000	0	15%	6%	47%	37%	61%	25%
1000	50	15%	6%	47%	41%	62%	25%
1000	100	16%	6%	48%	44%	64%	26%
1000	1000	21%	8%	59%	/	/	33%
10,000	0	5%	2%	14%	11%	19%	8%
10,000	100	5%	2%	14%	11%	19%	8%
10,000	1000	5%	2%	15%	13%	20%	8%
10,000	10,000	6%	3%	18%	25%	26%	11%

* The uncertainty was not provided when the thoron concentration was below the lower detection limit, which might not be able to be accurately estimated through Equations (18)–(20).

presents the expanded relative measurement uncertainty (k = 2) of the thoron measurement devices evaluated in this study. As displayed in Table 3, the measurement uncertainty of all devices decreased as the concentration of thoron increased, and increased with as concentration of coexisting radon increased. Similarly to Table 2, Table 3 stresses that the airflow-through scintillation cell exhibited the most favourable measurement uncertainties regardless of the concentration of thoron and coexisting radon, and could achieve a measurement uncertainty below 10% when the concentration of thoron was higher than 1000 Bq m⁻³, which is foundational in ensuring an acceptable level of uncertainty in calibration as a measurement standard device. The outstanding performance of the airflow-through scintillation cell can be mainly attributed to its high sensitivity and disengaged measurement time, as further elaborated in the Discussion section.

4. Discussion

An important contribution of this study is the use of a compartment model to address the progeny accumulation effect. Numerous studies have taken advantage of the compartment model to calculate the behaviour of radon/thoron and their progeny in various scenarios. Sakoda et al. developed a numerical model to predict the behaviour of radon and its progeny in the airflow-through cell and suggested the performance a similar study on thoron in future research [34]. This study further developed this methodology and provided the complete derivation procedure from the conception of the compartment model to the final algorithm for correcting the progeny accumulation effect and estimating thoron concentration. The normalised accumulation function and accumulation effect coefficient were proposed as and found to be the pivotal concepts for understanding and estimating the progeny accumulation effect. All the formulas were derived analytically, making them broadly applicable to all kinds of the airflow-through cell for thoron measurement, as demonstrated on a PIPS device in this study. This methodology would also be helpful for spectrum-type devices as the energy peaks of ²²⁰Rn and ²¹²Bi commonly overlap due to their adjacent energies (6.29 MeV and 6.05 MeV), and the effect of overlaps could be estimated using the proposed theoretical approach. Furthermore, in radon measurement, there is generally an equilibrium process of three hours, which is led by a change of radon progeny. This study has demonstrated the estimation of the change of thoron progeny using a compartment model. Therefore, it is possible to correct the non-equilibrium state and improve the response speed of radon measurement devices using the same methodology. Further research is recommended to explore the feasibility and potential benefits of using compartment models in radon measurements.

As noted in the Introduction section, the airflow-through scintillation cell is incapable of distinguishing between thoron and radon, which is a significant limitation in practical applications, as radon coexists with thoron in most cases. However, this limitation can be overcome by simultaneously measuring radon in the environment using an ancillary measurement device and deducting the radon signal from the measurement result of the scintillation cell as background. Numerous commercial and research-oriented devices meet this requirement. Here, we proposed a specific ancillary measurement device that uses a similar scintillation cell, as shown in Figure 6. This ancillary measurement device contained an additional gas storage chamber of 2.0 L between the inlet and the scintillation cell and applied a low flow rate of 0.2 L min⁻¹. As a result, the thoron almost completely decayed in the storage chamber due to its short half-life (55.6 s). Additionally, the decay products were prevented from entering the scintillation cell by a filter. Therefore, this ancillary measurement device was only sensitive to radon, and it was easy to estimate the radon signal of the scintillation cell from the measurement result of the ancillary measurement device and the sensitivity coefficient of the two devices obtained from the calibration. In conclusion, both the thoron and radon concentration in the environment could be determined using an airflow-through scintillation cell and an ancillary measurement device (a similar airflow-through scintillation cell with a large gas storage chamber which operated at a low flow rate).

This study compared the performance of the airflow-through scintillation cell, grab-sample scintillation cell, and PIPS device in terms of their lower detection limits and measurement uncertainties, which offered valuable insights into the comparative advantages of the airflow-through scintillation cell method. Previous studies have estimated the lower detection limit and measurement uncertainty of the grab-sample scintillation cell using similar devices [18,20]. Zhang et al. reported lower detection limits (at the 95% confidence interval) of 303 Bq m⁻³, 404 Bq m⁻³, 584 Bq m⁻³ and 1074 Bq m⁻³ for the grab-sample scintillation cell when the interfering radon concentrations were 0 Bq m⁻³, 50 Bq m⁻³, 200 Bq m⁻³, and 1000 Bq m⁻³, respectively [18]. Our results presented in Table 2 indicate a very similar performance of the scintillation cell used in our study due to the similarity between the devices. Our previous study estimated the relative standard uncertainty of the grab-sample scintillation cell to be around 24% when the concentration of ²²⁰Rn was 1000 Bq m⁻³ and when the concentration of ²²²Rn was 50 Bq m⁻³ [20], which was in accordance with the finding presented in Table 3. Those consistent findings suggest the reliability of the results presented in Table 2 and Table 3. These results presented in Table 2 and Table 3 suggested that the airflow-through scintillation cell technique realised in this study had the most prominent lower detection limit and measurement uncertainty compared to other techniques evaluated, was competent in the low-level thoron survey and used as a standard device for calibration. The outstanding performance of the airflow-through scintillation cell can be mainly attributed to its high sensitivity and disengaged measurement time, even though the compensation made due to the progeny accumulation effect does increase the uncertainty. Although the grab-sample scintillation cell had a similar sensitivity and intrinsic background, its lower detection limit and measurement uncertainty were limited by its short measurement time, which was dictated by its principle. On the other hand, although the PIPS device had a much lower intrinsic background, it had a considerable distance to the cover compared to the airflow-through scintillation cell, since its sensitivity is one order of magnitude lower. Moreover, as the level of coexisting radon increased, the background due to radon negated this advantage, and thus its detection limit decreased faster than that of the scintillation cell did. It is important to note that the devices tested in this study are not exhaustive and are not representative of all available devices. Therefore, the results should not be used to make broad conclusions about all thoron measurement devices. However, based on the above analysis, we believe that the prominent lower detection limit and measurement uncertainty of the airflow-through scintillation cell are universally valid due to its generally high sensitivity.

5. Conclusions

The present study established a reliable and practice method for thoron gas measurement using an airflow-through scintillation cell, with a correction for the progeny accumulation effect. The normalised accumulation function and accumulation effect coefficient were proposed in this study and found to be the pivotal concepts for understanding and estimating the progeny accumulation effect. The results indicated that this measurement technique achieved a lower detection limit below 100 Bq m⁻³ even with the presence of that of 100 Bq m⁻³ of radon, and attained a measurement uncertainty (k = 2) below 10% when the concentration of thoron exceeded 1000 Bq m⁻³. These results demonstrate the exceptional performance of the airflow-through scintillation cell technique for thoron gas measurement, making it a suitable method for low-level thoron surveys and as a standard device for calibration. The technique described in this study has been applied to the measurement standard device at SIMT for nearly 10 years, and an international comparison has shown its favourable precision among that of the measurement standard devices of four institutes [40].

A significant strength of the present study is that a systemic theoretical approach was proposed to estimate and correct the progeny accumulation effect in an airflow-through scintillation cell based on a compartment model. This methodology might also be helpful for spectrum-type devices in dealing with the overlaps of the energy peak of ²²⁰Rn and ²¹²Bi. Moreover, it is expected to improve the response speed of radon measurement devices. Consequently, further research is recommended to explore the feasibility and potential benefits of using compartment models in thoron and radon measurements.

Overall, this research will promote the field of thoron gas measurement and calibration, and is expected to facilitate the assessment and prevention of thoron radiological risks, helping to ensure the safety of the public, who may be exposed to thoron.

6. Patents

The technique of correcting the progeny accumulation effect described in this paper is the subject of a patent application (patent no. 201911163161.1) in China filed by some of the authors. The patent application has not yet been granted, but if it is approved, some of the authors could potentially benefit financially from its commercialisation. A complete list of the inventors of this patent application includes Chao Zhao, Yanliang Chen, Hui Zhang, Fangdong Tang, Linfeng He, and Yao Wang. Additionally, the obligee of this patent application is the Shanghai Institute of Measurement and Testing Technology, which is also the institute of the authors except for Dr. Weihai Zhuo in this manuscript.