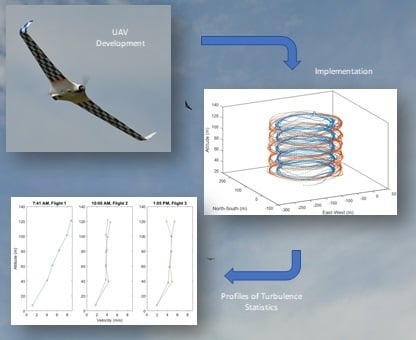
Development of an Unmanned Aerial Vehicle for the Measurement of Turbulence in the Atmospheric Boundary Layer

Abstract

This paper describes the components and usage of an unmanned aerial vehicle developed for measuring turbulence in the atmospheric boundary layer. A method of computing the time-dependent wind speed from a moving velocity sensor data is provided. The physical system built to implement this method using a five-hole probe velocity sensor is described along with the approach used to combine data from the different on-board sensors to allow for extraction of the wind speed as a function of time and position. The approach is demonstrated using data from three flights of two unmanned aerial vehicles (UAVs) measuring the lower atmospheric boundary layer during transition from a stable to convective state. Several quantities are presented and show the potential for extracting a range of atmospheric boundary layer statistics.

1. Introduction

By acting as the boundary to the atmosphere, the earth’s surface introduces forcing into it through frictional drag, evaporation and transpiration, heat transfer, pollutant emission and surface geometry. These interactions produce the highly turbulent atmospheric boundary layer, the lowest 200 to 2000 m of the atmosphere, separated from the free atmosphere above it by the capping inversion, which prevents mixing and dampens turbulence. Turbulence production in the atmospheric boundary layer occurs through a balance of shear stress introduced by the mechanical friction between the surface and air, as well as by buoyancy effects introduced by surface heat flux through temperature and humidity gradients. These buoyancy effects, subject to the diurnal cycle, produce stable, neutral, and unstable conditions within the atmospheric boundary layer, which typically evolve with time scales in the order of 1 h [1].

The efficiency of the turbulence produced within the atmospheric boundary layer for transporting heat, mass and momentum drives its response to surface forcing and accelerates the exchange of these quantities between the surface and atmosphere. Turbulence is therefore a crucial component of atmospheric boundary layer physics and it is the complexity of turbulence, its dynamics, and its internal interactions that limit our understanding of the important transport processes that occur within it.

The governing equations for turbulent flow in the atmospheric boundary layer can be derived from the conservation of mass and momentum. Assuming that density changes are negligible (the incompressibility assumption), the conservation of mass simplifies to

$$\frac{\partial U_i}{\partial x_i}=0$$

(1)

where $U_i$ are the components of the wind velocity vector, and the quantity $x_i$ represents the components of the position vector. Here we adopt summation notation such that the components of the vector are indicated by $i=1,2,3$. Generally, the vector components in geodetic coordinates have index 1 positive to the East, 2 positive to the North, and 3 normal outward from the surface. The corresponding expression for the conservation of momentum is

$$\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}=-{\delta }_{i3}\left[g-\left(\frac{{\theta }_v^{\prime }}{\langle {\theta }_v\rangle }\right)g\right]-\frac{1}{\langle \rho \rangle }\frac{\partial P}{\partial x_i}+\nu \frac{{\partial }^2{U}_i}{\partial x_j^2}$$

(2)

where t is time, ${\delta }_{ij}$ is the Kronecker delta, g is the magnitude of the gravitational acceleration, and ${\theta }_v^{\prime }$ is the local perturbation of the virtual potential temperature from its mean value given by $\langle {\theta }_v\rangle$. Furthermore, $\rho$ is the density of the air, $\nu$ is its kinematic viscosity, and P is the local static pressure. We note that, for the scales of interest within the atmospheric boundary layer, the Coriolis effects are small and can be neglected. The brackets $\langle ·\rangle$ represent an averaged quantity. Equations (1) and (2) represent a closed system of equations, provided that the properties of air and its temperature can be determined from an equation of state and an energy conservation equation.

As turbulence is an unsteady, three-dimensional process, a statistical approach to its modeling is frequently taken. Commonly, this is through Reynolds averaging, whereby the instantaneous velocity $U_i\left(t\right)$ is decomposed into fluctuating $u_i^{\prime }\left(t\right)$ and average $\langle U_i\rangle$ components such that $U_i\left(t\right)=\langle U_i\rangle +u_i^{\prime }\left(t\right)$. By substitution of this decomposition into the conservation of mass and momentum equations and averaging the results, the Reynolds-averaged form of the governing equations

$$\frac{\partial \langle U_i\rangle }{\partial x_i}=0$$

(3)

and

$$\frac{\partial \langle U_i\rangle }{\partial t}+\langle U_j\rangle \frac{\partial \langle U_i\rangle }{\partial x_j}=-{\delta }_{i3}g-\frac{1}{\langle \rho \rangle }\frac{\partial \langle P\rangle }{\partial x_i}+\nu \frac{{\partial }^2\langle U_i\rangle }{\partial x_j^2}+\frac{\partial \langle u_i^{\prime }{u}_j^{\prime }\rangle }{\partial x_j}$$

(4)

can be found. We note that this process results in the introduction of the Reynolds stress tensor, which is defined as $-\langle \rho \rangle \langle u_i^{\prime }{u}_j^{\prime }\rangle$ although it is often simplified to $\langle u_i^{\prime }{u}_j^{\prime }\rangle$ in incompressible flows. The Reynolds stress tensor represents the modification of the mean flow due to the presence of turbulence. Through the introduction of the additional unknowns encompassed in the Reynolds stress tensor, the governing equations are no longer closed, and hence the Reynolds stress tensor must be modeled in order to produce a solvable system of equations.

Obtaining a spatial description of the components of the Reynolds stress tensor is therefore valuable for gaining an understanding of turbulent phenomena, and for testing and validating numerical models of turbulence. To accurately measure turbulence, one has to resolve the entirety of turbulent scales, which can range from the smallest dynamically important scales (in the order of millimeters) to the largest turbulent scales (in the order of the atmospheric boundary layer thickness). Turbulence data is frequently obtained in the form of temporal information through cup and sonic anemometers, which have a temporal response of 1–2 [2] and 20 Hz respectively and a spatial resolution of 10 s of centimeters.

As most sensors are mounted on fixed towers, to translate this temporal information into spatial information, Taylor’s frozen flow hypothesis [3] is commonly invoked using some suitably selected convection velocity (typically the local mean velocity). Taylor’s hypothesis has been found to work reasonably well for the smallest scales of turbulence, but it is generally accepted to be in error for the larger-scale, long-wavelength motions [4]. Nevertheless, because of a lack of suitable alternatives, Taylor’s hypothesis is still commonly applied under the general assumption that such an application has non-negligible errors. However, recent evidence suggests that the actual convection velocity could be wavenumber-dependent [5,6,7]. A recent analysis of numerical simulations [6] suggests that low-wavenumber (long-wavelength) signatures in experimental energy spectra characteristic of coherent structures could be an artifact of aliasing introduced by Taylor’s hypothesis. It has also been suggested that this aliasing could increase with Reynolds number as highlighted in recent high-Reynolds number measurements in the atmospheric surface layer [8], where interactions between the outer-layer coherent structures and near-wall turbulence were found to be obscured by Taylor’s hypothesis. Compounding these challenges diagnostically is the difficulty when working with a flow that is non-stationary, slow to transport past the tower, and subject to the diurnal stability cycle, as selection of the convective velocity can be subjective when the mean flow is poorly defined [8,9,10]. Therefore, there is a clear need for a measurement technique capable of spatially sampling the atmospheric boundary layer turbulence over its entire range of scales and to capture enough of the largest scales within a sufficiently short time period to obtain statistical convergence.

The use of unmanned aerial vehicles (UAVs) to conduct measurements in the atmospheric boundary layer has the potential to address this need to obtain a spatial description of the structure and organization of turbulence. The ability of a UAV to use a high-temporal response sensor to spatially sample the flow field translates into a spatially sampled flow field with reduced reliance on Taylor’s flow hypothesis. In addition, within the 30 min period of quasi-stationarity within the atmospheric boundary layer [1], an UAV will be able to collect substantially more data than a fixed-point measurement, which requires the turbulence to convect past the measurement point. Finally, an UAV also has an advantage over fixed towers in terms of portability and the potential to measure in locations and altitudes where the construction of a tower is prohibitive.

Manned aircraft have been used to conduct atmospheric research for decades, conducting weather reconnaissance; measuring mean wind, temperature and humidity profiles; measuring atmospheric turbulence; and tracking pollutant concentrations (e.g., [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]). UAVs offer distinct advantages over manned aircraft, however, in their ability to safely perform measurements within meters of the surface and through greatly reduced operational costs [28].

The use of UAVs for atmospheric turbulence research is still in its infancy; although initially focusing on remotely piloted measurements of temperature, wind and humidity profiles [29,30], autopilot-guided measurements are now becoming increasingly common [31,32,33,34,35,36,37,38]. Typically, these measurements employ wind velocity probes with a temporal response that is little better than that of sonic anemometers. For example, Mayer et al. [39] have developed an UAV with meteorological equipment that estimates the wind vector by applying a constant throttle and measuring the ground speed. Data are sampled at 2 Hz, for a wavenumber of 0.11 m⁻¹ at the maximum speed of 18 m/s. Increasingly, UAVs are utilizing five-hole pressure probes [32,33,40], which can resolve to 40 Hz while flying at approximately 20 m/s.

In this paper, we describe the development of a fixed-wing UAV for conducting turbulence measurements of turbulence statistics in the atmospheric boundary layer. We also present sample data acquired by this system taken in as part of a large-scale CLOUDMAP (Collaboration Leading Operational UAS Development for Meteorology and Atmospheric Physics) test campaign.

2. Experimental Design and Methods

2.1. Data Reduction Approach

The use of aircraft as a research platform introduces an additional level of complexity and difficulty in measuring and analyzing atmospheric data, as a result of the highly dynamic properties and ever-changing state of the airborne platform. For turbulence measurements, this means that the wind velocity has to be extracted from the net air velocity signal measured by a sensor (e.g., a multi-hole pressure probe or hot-wire sensor) that has been mounted on a vehicle experiencing 6 degree-of-freedom rotation and translation. As a result, much work has been carried out over the previous decades to develop a suitable data reduction scheme [41,42,43], and the general approach is described here.

We assign the configuration of the body-fixed coordinate system on the aircraft whose origin is at its center of gravity and whose axes are aligned such that ${[x_1]}_B$ is directed toward the front of the aircraft, ${[x_2]}_B$ is directed outward in the starboard direction, and ${[x_3]}_B$ is directed toward the bottom of the aircraft. It is noted that ${[·]}_I$ denotes a vector in an earth-fixed inertial frame (with ${[x_1]}_I$ directed to the north, ${[x_2]}_I$ directed to the east and ${[x_3]}_I$ directed down), and ${[·]}_B$ is used to denote a vector in the vehicle-fixed body frame. The vehicle is assumed to be equipped with a velocity sensor aligned with the vehicle axis but mounted at a distance from the center of gravity of the vehicle, where ${\mathit{r}}_{S-CG}$ denotes the vector that points from the center of gravity to the measurement volume of the respective wind sensor. We also assume that the vehicle is equipped with an inertial navigation system (INS) or sensors, located at, or near, the center of gravity, which can determine the translational position and velocity, ${\mathit{r}}_{UAV}$ and ${\mathit{U}}_{UAV}$, respectively. In addition, we assume that the rotational position, indicated through the Euler angles of pitch, roll and yaw ($\theta$, $\varphi$ and $\psi$, respectively) and the angular velocity ${\mathsf{\Omega }}_{UAV}$ are also provided by this system. Thus, the time-varying position and orientation of the vehicle are known.

To isolate the wind vector from the sensor measurements, we first note that the traveling probes will also sense the velocity of the plane relative to the velocity of the air in the atmosphere. Therefore, we define the recorded relative velocity as

$${\left[{\mathit{U}}_r\right]}_B={\left[{\mathit{U}}_S\right]}_B-{\left[\mathit{U}\right]}_B$$

(5)

where ${\mathit{U}}_S$ is the velocity vector of the sensing volume (i.e., the probe tip) and $\mathit{U}={\left[U_1{U}_2{U}_3\right]}^{\mathrm{T}}$ is the velocity vector of the atmosphere (i.e., the wind) in the body-fixed coordinate system. The components of the inertial frame are taken as $x_1$ oriented north, $x_2$ oriented east and $x_3$ oriented down. Assuming the air velocity sensor faces forward, it follows that ${\mathit{U}}_r={\left[U_{r1}{U}_{r2}{U}_{r3}\right]}^{\mathrm{T}}$ are the measured components of the relative velocity tangential, normal, and bi-normal to the sensor axis, and are thus the components of velocity measured by the respective sensor.

We consider the general case in which the applied sensor is capable of resolving these three components of velocity, such as with a multi-hole pressure probe or a three- or four-wire hot-wire probe in which a suitable data reduction scheme (i.e., such as provided by Wittmer et al. [44] or Döbbeling et al. [45]) has been used to convert the voltage measured by the anemometer into the velocity magnitude and direction.

We let ${\left[{\mathit{U}}_{UAV}\right]}_I$ denote the translational velocity of the vehicle and $\mathsf{\Omega }={[d\theta /dtd\varphi /dtd\psi /dt]}^T$ denote the vector of rotation rates, given by the vehicle’s INS, and we assume that this measurement is taken at the center of gravity. The velocity of the sensor in the body frame is given by

$${\left[{\mathit{U}}_S\right]}_B={\left[{\mathit{U}}_{UAV}\right]}_B+{[\mathsf{\Omega }\times {\mathit{r}}_{S-CG}]}_B$$

(6)

Next, we recall that a vector in the inertial frame is transformed into the body frame by ${[·]}_B={\mathit{L}}_{BI}{[·]}_I$, where

$$\begin{array}{cc}\hfill {\mathit{L}}_{BI}=& \left[\begin{array}{ccc}{C}_{11}\hfill & C_{12}\hfill & C_{13}\hfill \\ C_{21}\hfill & C_{22}\hfill & C_{23}\hfill \\ C_{31}\hfill & C_{32}\hfill & C_{33}\hfill \end{array}\right]\hfill \\ \hfill C_{11}=& cos\theta cos\psi \hfill \\ \hfill C_{12}=& cos\varphi sin\psi \hfill \\ \hfill C_{13}=& -sin\theta \hfill \\ \hfill C_{21}=& sin\varphi sin\theta cos\psi -cos\varphi sin\psi \hfill \\ \hfill C_{22}=& sin\varphi sin\theta sin\psi +cos\varphi cos\psi \hfill \\ \hfill C_{23}=& sin\varphi cos\theta \hfill \\ \hfill C_{31}=& cos\varphi sin\theta cos\psi +sin\varphi sin\psi \hfill \\ \hfill C_{32}=& cos\varphi sin\theta sin\psi -sin\varphi cos\psi \hfill \\ \hfill C_{33}=& cos\varphi cos\theta \hfill \end{array}$$

(7)

and $\varphi$, $\theta$, and $\psi$ are the roll, pitch, and yaw angles, respectively [46]. Similarly, a vector in the body frame is transformed into the inertial frame by ${[·]}_I={\mathit{L}}_{IB}{[·]}_B$, where ${\mathit{L}}_{IB}={\mathit{L}}_{BI}^{-1}={\mathit{L}}_{BI}^{\mathrm{T}}$.

This is a standard transformation matrix between the body fixed and inertial frames used in flight dynamics, with the inertial coordinate system having component ${\left[x_1\right]}_I$ along the north axis, component ${\left[x_2\right]}_I$ along the east axis and component ${\left[x_3\right]}_I$ directed into the earth. The wind velocity in the body frame is then

$$\begin{array}{cc}\hfill {\left[\mathit{U}\right]}_B& ={\mathit{L}}_{BI}{\left[\mathit{U}\right]}_I\hfill \\ & =\left[\begin{array}{c}{C}_{11}{U}_1+C_{12}{U}_2+C_{13}{U}_3\hfill \\ C_{21}{U}_1+C_{22}{U}_2+C_{23}{U}_3\hfill \\ C_{31}{U}_1+C_{32}{U}_2+C_{33}{U}_3\hfill \end{array}\right]\hfill \end{array}$$

(8)

Combining Equations (6) and (8) with Equation (5) leads to

$${\left[\mathit{U}\right]}_I={\left[{\mathit{U}}_{UAV}\right]}_I+{\left[\mathsf{\Omega }\right]}_I\times {\mathit{r}}_{S-CG}-{\mathit{L}}_{IB}{\left[{\mathit{U}}_r\right]}_B$$

(9)

Thus, the desired quantity ${\left[\mathit{U}\right]}_I$ can be determined from the measured velocities ${\left[{\mathit{U}}_r\right]}_B$, ${\left[{\mathit{U}}_{UAV}\right]}_I$, and ${\left[\mathsf{\Omega }\right]}_I$; the measured angles $\theta$, $\varphi$ and $\psi$; and the known vector ${\mathit{r}}_{S-CG}$.

In the case for which the applied sensor is a multi-hole pressure probe, an additional transformation step in the reduction scheme is necessary. Typical calibration procedures for these probes result in the sensor reporting the relative air velocity along with the aircraft’s angle of attack, $\alpha$, and sideslip angle, $\beta$, allowing for the calculation of all three components of velocity. The angle of attack and sideslip angle are used to transform the recorded relative velocity, ${\left[{\mathit{U}}_{\mathit{r}}\right]}_A$, into Cartesian components using the transformation ${\mathit{L}}_{BA}$ according to [42,47,48], defined as

$${\mathit{L}}_{\mathit{BA}}=D^{-1}\left[\begin{array}{c}1\\ tan\beta \\ tan\alpha \end{array}\right]$$

(10)

where D is the normalization factor defined as

$$\begin{array}{c}\hfill D=\sqrt{(1+{tan}^2\alpha +{tan}^2\beta )}\end{array}$$

(11)

The updated equation used to find the desired quantity ${\left[\mathit{U}\right]}_I$ when using the multi-hole pressure probe is thus

$${\left[\mathit{U}\right]}_I={\left[{\mathit{U}}_{UAV}\right]}_I+{\left[\mathsf{\Omega }\right]}_I\times {\mathit{r}}_{s-CG}-{\mathit{L}}_{IB}{\mathit{L}}_{BA}{\left[{\mathit{U}}_r\right]}_A$$

(12)

where ${[·]}_A$ denotes the additional aerodynamic coordinate system recorded by the multi-hole pressure probe.

Finally, an additional coordinate transformation is applied to transform the measured wind velocity from the north-east-down inertial system used in flight dynamics to the east-north-up inertial system used in meteorology.

2.2. Physical Components

This section describes an UAV developed for measurements of atmospheric turbulence and the instrumentation package developed for the aircraft with the capability of implementing the data reduction approach described in the previous section. This vehicle, referred to as BLUECAT5, was used in a series of flight experiments conducted as part of the first CLOUDMAP test campaign in Oklahoma, USA. The specific aircraft components presented here are those used for the Tuesday, 29 June 2016 flights conducted as part of this campaign. Further details of the measurement site are provided later.

The commercially available flying wing Skywalker X8 (manufactured by Skywalker Techology, China) is the airframe that was used as the foundation for BLUECAT5. This airframe was selected as the foundation as it features a wingspan of 2.1 m and a total payload of ≈0.5 kg without battery or other modifications, leading to a total weight of 5 kg. The removable wings and carbon fiber wing spars allow for sufficient portability of the system and minimal setup time. The aircraft is designed to be hand-launched and belly landed, eliminating its reliance on prepared runways. The fuselage of the Skywalker X8 also provides ample room and access for the avionics and measurement instrumentation systems. BLUECAT5 is fitted with its propulsion system at the rear of the fuselage, making use of an electric motor coupled with a carbon fiber folding propeller. The electric propulsion system provides greater simplicity when compared with gasoline and nitromethane engines, leading to higher reliability but resulting in reduced endurance. The Axi Model Motors (Czech Republic) 4120/14 brushless electric motor used on BLUECAT5 requires a 4S 8000 mAh battery utilizing a Castle Creations, USA Phoenix Edge Lite 75 electric speed controller. This combination, combined with the relatively lightweight airframe and the large wing area of the aircraft, results in efficient power usage and flight times of close to 45 min at 17 m/s cruise speeds. With this motor and battery combination, the final payload capacity for meteorology equipment is approximately 0.5 kg.

Because the Skywalker X8’s fuselage provided sufficient space for excess payload and because of the sufficient aerodynamic properties of the aircraft, no significant modifications to the airframe were necessary, aside from changes required to mount the sensors in the nose and to fix the avionics and instrumentation packages within the payload bay. A BLUECAT5 aircraft and associated launcher system are displayed in Figure 1.

Pixhawk commercial autopilots (3DRobotics, USA) running the open-source ArduPilot software were used to convert the airframes for waypoint following flight. The Pixhawk is a high-performance autopilot suitable for both fixed-wing and multi-rotor configurations. By measuring the 6 degree-of-freedom attitude and rate information, the Pixhawk is able to provide the necessary outputs to the airframe control surfaces and propulsion motor(s) to control the aircraft’s flight.

The autopilot unit was mounted near the center of gravity and along the centerline of the BLUECAT5 airframe facing forward through the nose. The pulse-width modulated control surface outputs were wired out of the rear of the autopilot to the respective servo in the wings as well as to the electric propulsion motor. The Pixhawk was integrated with a 3DR uBlox global positioning system (GPS) with a compass to provide the position and ground velocity information of the aircraft. This unit was mounted on top of the aircraft along the centerline, which provided a clear view of the sky for the GPS and distanced the sensor from the electric propulsion motor causing interference to the magnetic compass. In addition, a Pitot-static tube mounted in the nose of the aircraft was used to provide airspeed information to the autopilot.

The autopilot is designed to fly in a pattern described using predetermined waypoints defined by altitude, latitude and longitude. These waypoints are designated within the ground station software (Mission Planner) installed on a laptop and used to control the aircraft’s flight path. While in flight, the ground station is used to monitor the aircraft behavior and flight properties, such as the heading, attitude, velocity, and altitude. In addition to observing the aircraft, the ground control station is used to alter flight paths, change flight modes, and adjust certain control parameters used for waypoint tracking flight. The communications between the aircraft and ground control station are accomplished via a 900 MHz radio telemetry link between an on-board 3DR, a USA telemetry radio and an identical radio connected to the ground station computer. While the parameters and waypoints are adjusted via the ground station, the information is stored on-board the Pixhawk hardware in the aircraft. This means that if the connection was lost between the ground station and the UAV, the UAV is able to continue its flight between waypoints. Upon completion of the flight plan, the UAV will enter a failsafe mode if a connection has not yet been established in which the UAV will return to a home waypoint, determined by the position at which the Pixhawk was armed, and loiter until a connection is re-established. This link is always connected prior to takeoff using the Mission Planner software.

In addition to supporting waypoint tracking, the open-source autopilot records the 6 degree-of-freedom position, velocity, and GPS information needed for the data reduction at 50, 10, and 5 Hz, respectively. This information is recorded by both the ground control station via telemetry and at the increased frequencies listed above to the micro SD card supported by the Pixhawk. This log file can then be recovered and transferred after landing by the SD card. Initially, the data reduction described in Section 2.1 was intended to be conducted using this information. However, numerous preliminary flight tests revealed that bias was introduced in the resolved wind vector by small inconsistencies in the reported attitude and attitude rate vectors. It was determined that the greatest source of this bias was the magnetometer, used to determine aircraft yaw in the inertial frame. Thus, a more accurate INS was required, which did not rely on magnetometer data.

The VN-300 manufactured by VectorNav, USA was selected, as it is an extremely small INS that utilizes dual GPS antennas to provide highly accurate heading measurements without the reliance on the magnetic sensors that are typically used. With the aid of advanced Kalman filtering techniques, the VN-300 provides a heading accuracy of 0.3° and a pitch/roll accuracy of 0.1° with a ground velocity accuracy of $\pm 0.05$ ms⁻¹. The INS also provides an increased sample rate of up to 400 Hz for all the variables; however, a 200 Hz sample rate was used for the experiments. The VN-300 outputs a custom binary file that is programmable within the software provided with the system. The outputs from the INS for this experiment were attitude angles $\theta$, $\varphi$, and $\psi$; rates ${\left[\mathsf{\Omega }\right]}_I$; and velocities ${\left[{\mathit{U}}_{UAV}\right]}_I$; along with temperature, pressure, latitude, longitude and altitude. The provided software was required to run the VN-300 and was installed on the on-board personal computer.

The UAV was equipped with a 30 cm long, 3.175 mm diameter brass rcats-120 Pitot-static tube produced by RCAT Systems, USA to provide the autopilot with an accurate true airspeed reading needed to maintain controlled flight. In addition, the Pitot-static tube was used to provide a reference static pressure for the turbulence measurement system. The true airspeed information was also used in the data reduction as a reference velocity signal for cross-correlating the autopilot telemetry signal with the turbulence measurement system velocity signal. This Pitot tube was mounted 25 cm in front of the nose of the aircraft away from the fuselage, 3 cm below the five-hole probe. The transducer used with the Pitot-static tube and autopilot was acquired using a Freescale Semiconductor MPXV7002DP differential pressure transducer with a 2 kPa range.

To increase the safety and reliability of takeoffs, a launching system was developed in order to propel BLUECAT5 into flight. The designed launcher consisted of a bungee system to pull the aircraft along a pair of rails providing the required angle of attack and airspeed for liftoff. The launcher base was created from 25.4 mm polyvinyl chloride (PVC) pipe to provide a low-friction rail system for the aircraft. The launcher was 2 m long and set at a 13° angle ideal for takeoff.

To measure turbulence in the atmospheric boundary layer for each BLUECAT5 UAV, the on-board instrumentation included a five-hole probe, pressure transducers, a data acquisition unit (DAQ), and an on-board personal computer (PC). The geometry of the five-hole probe produced a different pressure at each of the five ports on its surface, relative to the static pressure measured by the Pitot-static tube used by the autopilot. The pressure transducers converted these pressure readings to a voltage, with their high-level inputs connected to the different ports of the five-hole probe and the reference ports connected to the static line from the Pitot-static tube. The voltages from the pressure transducers were digitized by the data acquisition system, which was controlled by the on-board computer that also stored all the information produced by the INS and the DAQ. These components are discussed in further detail below, and the connectivity of this system is summarized in Figure 2.

Multi-hole probes are designed to determine the magnitude and direction of the local air velocity vector. Specifically, on aircraft, they provide the angle of attack and side-slip angles typically denoted by $\alpha$ and $\beta$, respectively. The five-hole probe is made up of a cylindrical body with one hole along the centerline and four holes evenly spaced cylindrically around an angled tip. Therefore, if the flow of the fluid is not aligned with the center of the probe, each hole reads a different pressure, which, through calibration, can be used to estimate $\alpha$, $\beta$ and the velocity magnitude.

The five-hole probe used for the present work was manufactured using a Formlabs, USA Form1+ Desktop Stereolithography 3D Printer. The five holes on the sensors are 1.2 mm in diameter and the tip of the probe has a 30° tip angle. Each hole is connected to a differential pressure transducer through 1.75 mm diameter Tygon tubing protected by a 25 cm aluminum tube. The probe was mounted along the ${\left[x_1\right]}_B$-axis, 25 cm in front of the fuselage and 60 cm away from the autopilot to minimize flow disturbances caused by the airframe. The five-hole probe pressure measurements were acquired using TE Connectivity, Switzerland 4515-DS5A002DP differential pressure transducers with a 0.5 kPa range. A custom circuit board was designed and constructed, providing a compact layout for all five transducers with optional inputs for first order resistor-capacitor low-pass filters. A 100 Hz anti-aliasing low-pass filter was designed and implemented prior to the signal being sent to the data acquisition system. These transducers were powered by the 5 V output from the DAQ. Before flight, each five-hole probe was calibrated using a $0.3$ m × 0.3 m wind tunnel. In order to complete the calibration, a custom traverse using Vexta stepping motors was designed and mounted to the wind tunnel, allowing the probe to both pitch and yaw in with a step accuracy of 0.36°. The calibration followed a standard calibration technique outlined by Treaster and Yocum [49] on the basis of the Wildmann et al. [50] study, which showed better results in comparison to the Bohn et al. method [51]. For the calibration, the wind tunnel was set to a constant velocity, in this case 17 m/s, as this was the cruise speed for the experiments, and the five-hole probe was stepped by 1° intervals between predetermined pitch and yaw angles of −15° and 15° for the pitch and −18° and 18° for the yaw. At each angle, the current pressure values at each hole were measured and averaged over 5 s. Additionally, a fixed Pitot-static tube was mounted into the wind tunnel to measure the dynamic pressure throughout the calibration, as well as to provide a static reference for the five-hole probe transducers. After the data was acquired from the calibration, the required coefficients were determined a posteriori so that the wind direction and magnitude could accurately be calculated from the pressure at each of the five holes of the probe.

Two identical BLUECAT5 aircraft were used for these experiments and consequently two different five-hole probes were utilized, each requiring separate calibration. The two five-hole probes were identified by the monikers Kirk and Spock; for both $\alpha$ and $\beta$, the root-mean-square error (RMSE) was under 0.15° and the RMSE for the measured velocity ${\mathit{U}}_{\mathit{r}}$ was well under 0.1 ms⁻¹, as shown in

Table 1. Root-mean-square error (RMSE) of calibration results.

Coefficient	Kirk RMSE	Spock RMSE
$\alpha$	0.0984°	0.1250°
$\beta$	0.0976°	0.1248°
$C_q$	0.0056	0.0099
$|U_r|$	0.05 ms−1	0.09 ms−1

. A coarse uncertainty propagation analysis [52] of Equation (9) was conducted using these values in concert with the stated uncertainties of the dual-GPS INS system. The result provides an estimate of the extracted wind vector error at 0.07 m/s, driven largely by the uncertainties in the dual-GPS INS and in the five-hole probe velocity magnitude. However, such analysis is unable to account for unknown biases, particularly in orientation, which could increase the uncertainty further.

An additional calibration was conducted to determine the frequency response of the five-hole probe. This was performed by subjecting the measurement tip of the probe to a step change in pressure and measuring the voltage output of the transducers. The results showed a slightly underdamped response, with a corresponding frequency response of 60 Hz. At the typical cruise speed of BLUECAT5, this frequency response translates to a spatial measurement resolution of approximately 0.28 m.

Interference effects between the airframe and five-hole probe were mitigated by placing the probe measurement volume 18 cm in front of the nose of the aircraft. This location was selected following scale-model tests of the aircraft, in which dye was injected into a water tunnel containing a model of the Skywalker X8 airframe and the deflection of the dye around the airframe was examined. This water tunnel flow visualization, shown in Figure 3a, was coupled with a full-scale wind tunnel test, in which a Pitot-static tube was positioned at various streamwise positions upstream from the aircraft nose and was used to measure the local velocity magnitude. For the wind tunnel tests, two vertical positions were tested, corresponding to the position of the Pitot-static tube (position 1) and five-hole probe (position 2). Vertical position 1 was located at the leading edge of the aircraft and vertical position 2 was 1.5 cm above it. The difference between the velocity measured at these locations and the true wind tunnel velocity are presented in Figure 3b. From Figure 3a, the streamline deflection was limited to a region very near (less than 5 cm) to the airframe, and the flow deceleration was limited to 16 cm upstream from the nose of the aircraft.

To measure the temperature and humidity during flight, an InterMet Systems, USA iMet-XQ UAV sensor was used, which provided a standalone solution for temperature and humidity measurements. The sensor includes a GPS receiver, and pressure, temperature and humidity sensors all powered by a rechargeable battery. Up to 16 MB of data from the sensors can be stored on board and downloaded post-flight for analysis via USB connection. The iMet humidity sensor supports a full 0–100% relative humidity (RH) range at a ±5% RH accuracy with a resolution of 0.7% RH. The on-board temperature sensor provides a ±0.3 °C accuracy with a resolution of 0.01 °C up to a maximum of 50 °C. The response times of these sensors are in the order of 5 and 2 s respectively in still air with the iMet-XQ UAV system sampling these sensors at 1 Hz.

The data acquisition system used to digitize the voltage output from the five pressure transducers as well as the voltage input to the transducers, was a Measurement Computing, USA MCC USB-1608FS-Plus DAQ. This particular unit is capable of recording eight single-ended analog inputs simultaneously at 16 bit resolution with rates of up to 400 kS/s. The DAQ also provides a 5 V signal to power the pressure transducers. During the experiments, the DAQ recorded six channels simultaneously at 1 kHz for each channel (corresponding to 6 kS/s).

The DAQ was connected via USB to an InFocus, USA Kangaroo Mobile Desktop Computer KJ2B#001-NA with an Intel Atom X5-Z8500 (1.44 GHz) processor, 2 GB LPDDR3 RAM and 32 GB eMMC storage running the Windows 10 home operating system. A custom Matlab script was written to control the acquisition, compiled as a standalone executable. This script allowed for the selection of the channels to be recorded, the duration of the acquisition, and the voltage range at which each channel was recorded. The Kangaroo PC was also used to simultaneously run the VN-300 INS system by using the manufacturer-provided software. The on-board PC stored all the recorded data on its 32 GB hard drive from both the DAQ and the additional INS. Data from both systems were stored on the PC and then transferred off the aircraft post-flight for archiving and further analysis.

2.3. Sonic Anemometer

To provide a ground reference for the wind velocity vector and temperature during flights, an R.M. Young, USA Model 81000 ultrasonic anemometer was used. The sonic anemometer is a three-axis wind sensor that provides the three components of velocity in the inertial reference frame, as well as a sonic temperature measurement. The Young 81000 can measure wind speeds of up to 40 m/s at a resolution of 0.01 m/s with an accuracy of ±0.05 m/s. From the three components of velocity, the direction of the wind can be provided in 360° at a resolution of 0.1° with an accuracy of ±2°. The temperature provided by the sonic anemometer is calculated on the basis of the speed of sound, leading to a temperature measurement accuracy of ±2 °C. For the data reported here, the anemometer was set to output four analog voltages, corresponding to $U_1$, $U_2$, $U_3$ and the temperature.

The sonic anemometer was mounted onto a 7.62 m tower and the voltage data output from the anemometer was recorded by a stand-alone high-speed Measurement Computing, USA LGR-5329 multifunction data logger, logging at 100 Hz. Both the anemometer and logger were powered by a single 4S 3300 mAh lithium/polymer battery.

2.4. Measurement Procedures

The primary data sets acquired for this work were taken with two BLUECAT5 UAVs flying simultaneously with varying flight paths. Each UAV was equipped with identical five-hole probe sensor packages. Before each flight, the instrumentation was started manually through the on-board Kangaroo PC, and the autopilot was connected to its respective ground station. At the start of the data acquisition, zero reference voltages were taken by applying a cover to both the five-hole probe and the Pitot-static tube in order to mitigate any wind velocity the sensors might have been reading at ground level. The aircraft were then launched sequentially via the use of the custom-made launcher under manual control. Once positive flight characteristics were confirmed through manual flight, the aircraft were switched to a waypoint tracking flight mode, at which point the autopilot began flying its flight path, defined using predetermined waypoints. Following approximately 30 min of flight time, the aircraft were returned to manual mode and recovered via belly landing. Immediately after each flight, all relevant flight data, including the five-hole probe voltage readings, autopilot logs, VectorNav information and iMet-XQ UAV files, were transferred to a laptop for validation checks and archiving on an external hard drive. The Kangaroo PCs and iMET-XQ UAV sensors and flight batteries were then replaced with counterparts containing full charge, making the aircraft ready for the next flight following an approximately 15 min turnaround time.

All the flights were flown under the University of Kentucky’s FAA Blanket Area Public Agency Certificate of Authorization number 2016-ESA-32-COA.

2.5. Implementation of Data Reduction

In order to implement the data reduction scheme described in Section 2.1, the inertial data from the VectorNav INS consisting of the UAV’s velocity, Euler angles, and Euler angle rates were needed in conjunction with the airspeed and direction given by the five-hole probe. The five-hole probe data were sampled by the on-board data acquisition system at 1 kHz, whereas the VN-300 INS sampled the inertial data at 200 Hz. In fact, between the four separate data systems that were described earlier in this section, including the five-hole probe data acquisition system, the Pixhawk autopilot, the VectorNav VN-300 INS, and the iMet-XQ UAV temperature and humidity sensor, each system was established with varying acquisition rates and start times during the experiments. The acquisition rates for each system can be found in

Table 2. Acquisition rates for on-board instrumentation systems.

System (Component)	Acquisition Rate
Pixhawk (6-DoF attitude)	50 Hz
Pixhawk (Airspeed and barometric pressure)	10 Hz
Pixhawk (GPS data)	5 Hz
iMet-XQ	1 Hz
USB-1608FS-Plus data acquisition unit	1000 Hz
VectorNav VN-300 INS	200 Hz

. Because of this, the first step to the data reduction was to align the respective data systems’ time series and re-sample the data at a consistent rate.

To complete the alignment between the VN-300 INS and the five-hole probe data, the Pixhawk autopilot was used as a reference signal to which the other data systems were aligned. The Pixhawk’s GPS velocity, measured at 5 Hz, was used to align the VN-300 INS, and the Pixhawk’s air velocity data, measured at 10 Hz, was used to align the five-hole probe measurements. This was done firstly by assuming that the UAV position and orientation smoothly transitioned between sample points in the data log, allowing for interpolation of the relevant Pixhawk data to 200 Hz using a cubic interpolation scheme. Similarly, the five-hole probe data was re-sampled from 1 kHz to 200 Hz, as the filter used for the pressure transducers was set to a 100 Hz cut-off frequency. With the data set to identical sample rates, the relative time difference between the start of each set of time series data was then determined by cross-correlating the Pixhawk data with the respective data from the sensors recorded by the DAQ and VN-300 INS. Before correlation between the five-hole probe data and the Pixhawk’s airspeed data, the voltage output from the central hole on the five-hole probe was converted to velocity so that the information being correlated represented the same measurement. Identification of the location of the maximum in the cross-correlation allowed for determination of the relative shift between the initiation of sampling between the INS and five-hole probe and the Pixhawk data, consequently aligning the two INS and five-hole probe data streams. As a result, ${\left[{\mathit{r}}_{UAV}\left(t_i\right)\right]}_I,{\left[{\mathit{U}}_{UAV}\left(t_i\right)\right]}_I,{\left[\mathsf{\Omega }\left(t_i\right)\right]}_I$ and the transformations $L_{IB}\left(t_i\right)$ and $L_{BA}\left(t_i\right)$ became known, where $t_i$ is the time corresponding to each discrete sample of the five-hole probe velocity, ${\left[{\mathit{U}}_r\left(t_i\right)\right]}_B$, and directions, $\alpha \left(t_i\right)$ and $\beta \left(t_i\right)$. From this information, the wind vector ${\left[\mathit{U}\right]}_I$ was calculated using Equation (12).

3. Results and Discussion

3.1. Measurement Site Overview

The results presented in this work are from flight experiments conducted on 29 June 2016, which began at approximately 07:40 CDT and were concluded at 13:30 CDT, in close proximity to the Marena Mesonet site in Marena, Oklahoma, USA. The Marena Mesonet site is part of the Oklahoma Mesonet, a network of 121 environmental monitoring stations spread across the state. The Mesonet consists of a 10 m tall tower containing multiple instruments to measure the environment every five minutes. The measurements provide parameters such as barometric pressure, RH, air temperature, wind speed, and wind direction between 0.75 and 10 m. The sonic anemometer tower was placed close to the Mesonet tower and was used to provide a reference wind and temperature measurement at 7.62 m. The objective of the flights was to demonstrate the use of two UAVs to simultaneously measure profiles of the atmospheric boundary layer properties by flying concentric flight paths at different radii and altitudes. The two aircraft are referred to as BC5A and BC5B. These two aircraft were identical in both hardware and capabilities. This technique allowed for the measurement of atmospheric properties at two altitudes within approximately the same vertical profile at the same time. With two altitudes being measured simultaneously, the impact of time evolution on the measured atmospheric properties could be somewhat mitigated.

A total of three flights were conducted, each acquiring data between 40 and 120 m above ground level, and the latter two were multi-UAV flights, as outlined in

Table 3. Wednesday, 29 June 2016 flights overview.

Flight #	BC5A Takeoff	BC5B Takeoff	Radius (m) A/B	Altitudes (m Above Ground)
Flight 1	07:41 CDT (UTC-5)	N/A	80/100	(40, 60, 80, 100, 120)
Flight 2	09:57 CDT (UTC-5)	09:58 CDT (UTC-5)	80/100	(40, 60, 80, 100, 120)
Flight 3	13:09 CDT (UTC-5)	13:05 CDT (UTC-5)	80/100	(40, 60, 80, 100, 120)

. For the multi-UAV flights, the BC5A airframe began its 80 m radius loiter flight trajectory at a 40 m altitude and at increased altitudes at 20 m steps every two minutes until it reached 120 m, before stepping back down to its starting altitude. BC5B mirrored BC5A’s profile pattern at a 100 m loiter radius, beginning at a 120 m altitude and descending to 20 m before ascending again up to 120 m. For each profile, the aircraft would loiter at an 80 m altitude, simultaneously providing an opportunity to compare data points at that position.

A graphical overview of the Marena measurement site using topography and imagery obtained from ArcGIS and Google Earth is shown in Figure 4, as well as a top-down view of the flight patterns for each UAV. The flight area elevation varied by ±2 m throughout the flight paths. The site is 327 m above sea level, located approximately 7 mi north of Coyle, OK, USA at $36.{064}^{\circ }$ N and $-97.{213}^{\circ }$ W. The terrain is largely rural grassland with small patches of trees and slightly rolling elevation. The flights took place near the N3250 gravel road (thick line running nearly North/South in Figure 4b) with the ground station located off of the Mesonet access road (thinner, S-shaped road running approximately East/West in Figure 4b), near the takeoff location marked by a green arrow on the map. The blue circles in Figure 4 represent BC5A’s programmed flight path, the red circles depict BC5B programmed flight path, the blue diamond represents the location of the sonic anemometer, and the green marker shows the location and direction of takeoff for each UAV.

The weather on the day of measurement was clear and partly cloudy. The corresponding temperature, RH and wind speed reported from 00:00 to 19:00 CDT on 29 June 2016 by the Mesonet station are presented in Figure 5a–c, respectively. The approximate times of the flights are indicated in these figures for reference. It can be observed from Figure 5a that for all three flights, the temperature gradient near the ground suggested convective conditions, and the first flight just followed a period of neutral stability. As the temperature increased, from the first to last flight, the RH on the ground dropped from approximately 70% to 50%, as shown in Figure 5b. Over the same period of time, as shown in Figure 5c, the wind speed near the ground remained relatively constant between 2 and 3 m/s.

3.2. Temperature and Humidity

The time traces of temperature measured by the UAVs over the three flights are shown in Figure 6 and reveal the combined altitude above ground level, z, and time dependence of temperature over the three flights. For flight 1, which was performed with a single UAV and is shown in Figure 6a, the profile shows an inversion of temperature at 40 m, decreasing slightly with z below 40 m and increasing at a much higher rate above it. Thus, flight 1 took place within a developing convective layer with a thickness of approximately 40 m, with the residual stable layer above it. Figure 6a also shows the time dependence of the temperature, indicated by the color of the symbol used. Groups of symbols indicate periods of time during which the aircraft loitered at a single altitude. Over the course of the 30 min flight, the temperature increased by approximately 2 °C.

For the two later flights, shown in Figure 6b,c, the temperature decreased with z for the entire range of altitudes measured. Between flights 2 and 3, it can be observed that there was both a decrease in the temperature change over the course of the flight and a corresponding increase in variability of temperature measured during a loiter at constant altitude.

The stability conditions and temperature variability are better reflected in the profiles of mean and variance of virtual potential temperature. The virtual potential temperature ${\theta }_v$ was calculated from the measured temperature T and the relative humidity $RH$, as follows:

$${\theta }_v=(1+0.61r){\theta }_e$$

(13)

where r is the vapor mixing ratio and

$${\theta }_e=T{\left(\frac{100000}{P}\right)}^{0.286}$$

(14)

is the potential temperature in kelvin, found from the measured temperature T and the measured static pressure P (in pascals). The vapor mixing ratio was found from the measured RH using

$$r=0.622\frac{P_v}{P-P_v}$$

(15)

where $P_v$ is the partial pressure of the water vapor found from the RH and temperature, as follows:

$$P_v=\frac{RH}{100}\frac{exp[77.345+0.0057T-\frac{7235}{T}]}{T^{8.2}}$$

(16)

The profiles of the mean virtual potential temperature $\langle {\theta }_v\rangle$ and the variance of the virtual potential temperature $\langle {\theta }_v^2\rangle$ measured by BC5A and BC5B for all three flights are shown in Figure 7 and Figure 8. These statistics were calculated by subdividing the time series into subsets consisting of measurements taken while the aircraft loitered at a prescribed altitude. As each aircraft loitered at a prescribed altitude twice during the same flight, there are two values of $\langle {\theta }_v\rangle$ and $\langle {\theta }_v^2\rangle$ for each z for a single flight trajectory. The separation in time of these values is altitude-dependent, as reflected in Figure 6. Also shown in these figures is the trend produced by averaging all the $\langle {\theta }_v\rangle$ and $\langle {\theta }_v^2\rangle$ values taken at the same altitude.

For comparison, the mean values measured by the sonic anemometer and the Mesonet are also shown in Figure 7, and the variance measured by the sonic anemometer is shown in Figure 8. To maintain similar statistical convergence, the sonic anemometer data measured during each flight has been divided into 5 min intervals, and statistics have been calculated for each of those 5 min intervals.

The mean virtual potential temperature profiles provided in Figure 7 show stability conditions consistent with the observations made from the temperature profiles that are consistent with a mixed layer. For flight 1, stable conditions persisted above the mixed layer, which reached only to 40 m. However for flights 2 and 3, the stability conditions were consistent with that of a mixed layer for the full range of altitudes measured. Interestingly, for flight 2, the UAV measurements show better agreement with the Mesonet station than the sonic anemometer.

These conditions are reflected in the profiles of the temperature variance, shown in Figure 8. For flight 1, which captured both stable and unstable conditions, the entrainment zone at the interface between the stable and mixed layers contained higher temperature fluctuations, most likely caused by the higher gradients of ${\theta }_v$ at this location. Even moderate vertical transport and intermittency cause higher fluctuations at this altitude, undoubtedly with some contribution from the $\pm 5$ m variability in the aircraft altitude that occurred during a loiter. For the two later flights, the convective conditions resulted in more constant temperature fluctuations with altitude. Interestingly, during flight 3, the sonic anemometer temperature fluctuations varied significantly during the flight, which suggested some strong temperature variability near the surface over the course of the measurement. This did not appear to be a measurement anomaly, as some of this variability was captured in the time traces of temperature taken by the UAVs near the ground, as shown in Figure 6c. It is not known what caused this variability near the surface.

Time traces showing the altitude and time dependency of the measured RH are shown in Figure 9 for each of the three flights. For flight 1, shown in Figure 9a, the RH near the surface was near 70%, decaying with altitude to approximately 55% at $z=120$ m. For the two later flights, shown in Figure 9b,c, the RH became more uniform, at approximately 60% and 50% respectively, extending throughout the measured altitudes. These values are consistent with those reported by the Mesonet site during the times the flights were conducted. We note that the effect of the slower time response of the humidity probe was evident during flight 1, appearing in the two far-left lines, which represent descents from a 120 to a 40 m loiter altitude. These two traces have a lower RH than other measurements made at the same altitude and reflect the lag in the instrument, as the slow response of the instrument caused its output to bias towards the RH at higher altitudes rather than the RH at the altitude of measurement. This bias should not have impacted the mean statistics measured at a constant altitude, although the humidity fluctuations would be severely filtered by this slow response.

To obtain a better impression of the moisture content, profiles of the mean vapor mixing ratio are provided in Figure 10. As for the profiles of the mean temperature, the vapor mixing ratio has been averaged over the period of time each UAV spent loitering at a constant altitude. The profiles show that while within the stable residual layer above 40 m in flight 1, the moisture content decreased with altitude, the flights within the mixed layer displayed a much more uniform moisture content, consistent with the more constant temperatures observed during these flights. No humidity data was available from the sonic anemometer tower, but the vapor mixing ratios measured by the UAVs were slightly lower than the values reported by the Mesonet station.

In general, for the two later flights, in which two UAVs were flying simultaneously, the measurements can be used as a form of self-validation of the UAV data systems, at least for precision errors. Most notably, this validation occurs in the altitudes around 80 m, as this was when both UAVs were simultaneously at the same altitude. As evidenced by Figure 7, Figure 8, Figure 9 and Figure 10, the measurements are in very good agreement and validate the instrumentation system and data reduction operation for the scalar quantities. We note, however, that because the airframes and instrumentation were identical, bias errors introduced by the airframe or instrumentation would not be detected by this comparison.

3.3. Wind Velocity

The time traces of the velocity magnitude measured by the UAVs over the three flights are shown in Figure 11, showing the combined altitude and time dependence of the wind velocity measured during the three flights. For flight 1, shown in Figure 11a, the velocity magnitude profile is consistent with a shear-driven boundary layer, as the velocity magnitude increases monotonically with z throughout the measured flight profile. This is consistent with flight 1 taking place within a developing convective layer that had a residual stable layer above it, as observed from the temperature profiles. The two later flights, shown in Figure 11b,c, are also consistent with the mixed layer conditions indicated by the temperature profiles. For flights 2 and 3, the wind velocity showed little variation with altitude but much greater variation in time, reflecting increasingly turbulent conditions. The variations in time also increased between flights 1, 2 and 3, suggesting that the turbulence intensity increased between all three flights.

These measurements of the three time-varying components of the wind velocity vector $U_i\left(t\right)$ allowed for the determination of the mean velocity components $\langle U_i\rangle$ as well as all the components of the Reynolds stress tensor $\langle u_i^{\prime }{u}_j^{\prime }\rangle$ at each flight level, by averaging the measurements taken while the aircraft loitered at each altitude. To aid with connecting the Reynolds stress components to the mean wind velocity, the coordinate system has been rotated to a coordinate system aligned with the mean wind vector, such that ${\langle U_1\rangle }^{*}$ is in the direction of the mean wind at each flight level, and thus ${\langle U_2\rangle }^{*}=0$. Here, we use a superscripted ∗ to indicate statistics taken in this mean-wind-fixed coordinate system. The corresponding profiles of the mean velocity are shown in Figure 12.

For the latter two flights with two UAVs flying simultaneously, the agreement of the measurements of both the mean wind speed and direction between them was good, with exceptional agreement when the UAVs were simultaneously at similar altitudes (i.e., in the range between 60 and 100 m). The greatest differences between the measured mean velocities occurred at the maximum and minimum altitudes, when the time difference between the measurements was greatest. The larger variation in the mean wind velocity measured during each loiter and the overall mean velocity at these altitudes therefore suggested that long-wavelength motions existed within the boundary layer during flight 3 and were not resolved within the time spent loitering at a fixed altitude. Although difficult to compare directly because of the 30 m difference in the measurement position, the wind velocities measured appeared to be consistent with the results reported by the Mesonet site. The time traces of the velocity magnitude shown in Figure 11, which extend down to the surface, show very good agreement with the Mesonet site values, however.

The changes in the boundary conditions are reflected in the scattering of the measured Reynolds stresses. This is conveniently summarized in the turbulent kinetic energy, defined as $k\equiv \frac{1}{2}\langle u_i^{\prime }{u}_i^{\prime }\rangle$, which describes the magnitude of the turbulent fluctuations. The measured profiles of k are provided in Figure 13. For the combined convective and stable boundary layer measured during flight 1, the overall turbulent kinetic energy was lower than that measured during later flights, despite the mean wind velocity being much higher. There was an increase in k within the entrainment layer, as also observed in the temperature fluctuations shown in Figure 8. However, this region of increased variability in the wind velocity magnitude is much broader than that observed in the variance of temperature. Once the boundary layer transitioned to a mixed layer, for flights 2 and 3, there was a corresponding increase in k, and the profiles exhibit increased scattering in the measured values of k, most likely due to an increase in long-wavelength motions. We note that although these long-wavelength motions increase the data scattering, when the aircraft were close to, or at the same flight level (between 60 and 100 m) there was very good agreement in the measured k. Furthermore, these long wavelengths were at least partially resolved by the trendline formed by averaging the measurements taken at a fixed altitude. This trendline shows an approximately constant k with altitude for the mixed layer conditions of flights 2 and 3.

As noted, a potential source of the scattering in k for later flights, particularly flight 3, was incomplete resolution of long-wavelength turbulent motions. The circular flight profile was designed to produce vertical profiles of mean quantities and Reynolds stresses, and was not well suited to extract information about the integral scales of turbulence or spatial spectra. However, a coarse estimate of the Kolmogorov scale, $\eta$, could be estimated following the homogeneous isotropic turbulence approximation:

$$\eta ={\left(\frac{{\nu }^2}{15{(\partial U_1/\partial x_1)}^2}\right)}^{1/4}$$

(17)

where $\nu$ is the viscosity. This quantity was approximated by finite differencing of the wind velocity in the direction of the flight path, and $\eta$ was found to be in the order of 2 mm, consistent with that expected in the atmospheric boundary layer [1]. We note that this is only a coarse estimate, as the frequency response of the five-hole probe was not sufficient to resolve scales of less than approximately 30 cm. Through the application of Taylor’s hypothesis, spatial cross-correlations were also calculated. These cross-correlations are not included here because of the imprecision of the calculation approach used. However, these correlations suggested the integral length scales were in the order of the flight altitude (50 to 100 m). Thus, at the measured mean wind speed, only approximately 5 to 10 integral length scales were captured during each loiter, which may have contributed to the data scattering observed in k and the Reynolds stresses.

To assess the scale dependence of the turbulence further, the frequency spectra calculated from the time series of $U_1$, $U_2$ and $U_3$ are presented in Figure 14a–c, respectively. These figures represent an amalgamation of the measurements from the different altitudes as, to improve the statistical convergence of the spectra, no attempt was made to segregate the different altitudes. The frequency spectra do show that the aircraft were able to resolve at least three decades of the inertial subrange, which is characterized by a $-5/3$ slope in the spectrum. Although not descriptive of the turbulence at each flight level (which would also require the wavenumber rather than frequency spectra), this result provides confidence that the measured k and Reynolds stresses reflect turbulence statistics, rather than system noise.

The contributions to the turbulent kinetic energy can be divided into the different normal components of the Reynolds stress tensor ${\langle u_i^2\rangle }^{*}$, which are presented in Figure 15. We note that to simplify the presentation, only the average values from all the flights at each flight level are shown and that, as with the mean wind velocity, the coordinate system has been rotated such that $x_1$ is in the direction of the mean wind, as indicated by the superscripted ∗. Consistent with shear-driven turbulent production (e.g., [53]), for all three flights, the streamwise component ${\langle u_1^2\rangle }^{*}$ was the greatest near the surface, as the kinetic energy of the mean flow was in this direction. For flight 1, there was a mean shear across the entire measurement domain, and hence the region of higher ${\langle u_1^2\rangle }^{*}$ was larger. However, for the later flights, the mean velocity shear was confined near the surface. Interestingly, the mean velocity gradient near the surface, as measured by the Mesonet station, remained largely unchanged during the three flights, suggesting that the shear-driven turbulence production also remained largely unchanged. Hence, the increase in the Reynolds stresses between flights 1, 2 and 3 could be attributed to the increased turbulence production by buoyancy-driven convection. At higher altitudes (generally above 80 m), the turbulence approached isotropy, particularly for the later flights, for which the boundary layer had transitioned to a mixed layer.

The remaining three components of the Reynolds stress tensor, specifically the shear stresses ${\langle u_1{u}_2\rangle }^{*}$, ${\langle u_1{u}_3\rangle }^{*}$, and ${\langle u_2{u}_3\rangle }^{*}$, are shown in Figure 16. As can be expected, the values of the shear stresses were much lower than the normal stresses, although they did increase in general as the boundary layer evolved. There was also much less organization evident in the shear stresses. It should be noted however, that the streamwise/surface normal component ${\langle u_1{u}_3\rangle }^{*}$ was consistently negative, as has commonly been observed in turbulent boundary layers (e.g., [53,54]) as a result of the prominence of sweeps and ejections, the motions responsible for the transfer of high-momentum fluid towards the surface and low-momentum fluid away from the surface.

4. Conclusions

An atmospheric sensing system consisting of an UAV paired with pressure, temperature, humidity and wind velocity vector sensors was developed for measuring turbulence in the lower atmospheric boundary layer. The capabilities of the system were demonstrated through three measurement flights taken over the course of a morning; the latter two flights were performed with two identical UAVs flying simultaneous, complimentary flight profiles. By comparison with a nearby ground-based meteorological measurement station, the results from the experiments suggest that the approach successfully extracts the wind vector alongside scalar statistics of temperature and humidity. A comparison between the statistics measured by the two aircraft flying simultaneously found them to be in good agreement, providing confidence in the repeatability of the measurements made by the UAVs. Frequency spectra calculated for the different components of the wind vector were consistent with expected turbulent frequency spectra behavior, providing confidence in the extracted Reynolds stresses and turbulent kinetic energy. A high level of data scattering for the last flight suggested that long-wavelength motions, which were present during that flight, were not well resolved by the flight profile chosen, as the aircraft did not loiter at a fixed altitude long enough to capture these motions.

The temperature profiles indicated that during the first flight, the boundary layer consisted of a shallow mixed layer, with a residual stable layer above it. The mean wind velocity within this boundary layer was in almost constant shear from the surface to the highest altitude measured. Conversely, the moisture content was observed to decrease with distance from the surface. The interface between the mixed layer and residual stable layer, at the lowest measurement locations, was characterized by locally high temperature fluctuations, with a much broader distribution of increased turbulent kinetic energy of the wind, and by highly anisotropic Reynolds stresses. For the second and third flights, the boundary layer characteristics were consistent with a mixed layer throughout the altitude range measured. The mean velocity, temperature and moisture content showed little variation with altitude, and the turbulent kinetic energy of the wind was significantly higher than for the first flight. The Reynolds stresses indicated that the turbulence was largely isotropic, except for the measurement location nearest to the surface, where the shear-driven turbulence production was the highest.