Deployment and Performance of an X-Band Dual-Polarization Radar during the Southern China Monsoon Rainfall Experiment

Abstract

An X-band dual-polarization radar (XPRAD) was deployed in Guangdong province as part of the Southern China Monsoon Rainfall Experiment (SCMREX) during the storm season in 2016. This paper presents a comprehensive assessment of XPRAD observations during SCMREX with emphasis on data processing and rainfall products. The differential phase-based attenuation correction and radar calibration using self-consistency of dual-polarization observables are presented. It is found that the standard deviation of the $Z_{dr}$ bias is less than 0.2 dB based on ‘light rain at low angle’ and ‘dry aggregate snow’ observations. Cross-comparison with two standard S-band China New Generation Weather Radars (CINRAD) shows that the bias of $Z_h$ has a mean value less than 1.5 dBZ and a standard deviation less than 0.5 dBZ. In addition, fifteen rainfall events that occurred during the intensive observing period (IOP) are analyzed to demonstrate the rainfall estimation performance of XPRAD. In particular, rainfall accumulations at 1-, 2- and 3-h scales derived using R($K_{dp}$) and R($Z_h$, $Z_{dr}$) relations are evaluated using national level rain gauge data and CINRAD-based rainfall estimation. The results show that both R($K_{dp}$)- and R($Z_h$, $Z_{dr}$)-based products agree well with the rain gauge observations and CINRAD estimation. The difference between $R(K_{dp})$ and $R\left(Z_h,Z_{dr}\right)$ is not significant, although $R(K_{dp})$ shows slightly better performance than $R\left(Z_h,Z_{dr}\right)$.

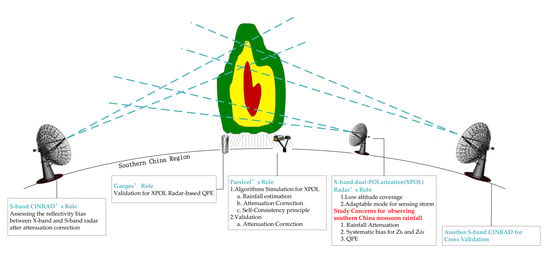
1. Introduction

Heavy rainfall annually occurs from mid-April to mid-June in southern China, often inducing flooding and geological disasters, causing devastating property damage and loss of life. Precipitation over this period, well-known as the southern China monsoon rainfall, accounts for nearly half of the total annual precipitation. However, quantitative precipitation estimation and forecasting (QPE/QPF) in this region remains a challenge since the monsoon mechanism is not yet well understood due to the complicated multiscale atmospheric processes involved [1]. In 2016, the Southern China Monsoon Rainfall Experiment (SCMREX) was conducted in order to further understand the physical mechanism of monsoon rainfall in the pre-summer season and improve the performance of QPE [1]. Weather radar was a key component of providing accurate quantitative precipitation estimations during the setup of SCMREX. Currently, there are 14 operational S-band China New Generation Weather Radars (CINRAD) in Guangdong province, providing routine weather observations for the whole province. However, the CINRAD radars operate through pre-defined scan strategies, which have a slow update rate of five–six min and cannot be changed. In addition, these S-band radars operate at long ranges (i.e., 460 km maximum), resulting in most of the lower atmosphere not being able to be observed due to the Earth’s curvature. On the other hand, the application of short range X-band radars is gaining more interest worldwide in recent years. X-band radar has some evident advantages, including higher mobility, smaller size, lower cost and power consumption, potentially higher spatial resolution and stronger differential phase signals. Some typical applications of X-band radar include: the X-band radar network for Collaborative Adaptive Sensing of the Atmosphere (CASA) [2,3,4], the X-band radar of NOAA/Environmental Technology Lab (ETL) for Hydro-meteorological Testbed (HMT-04) project [5], the mobile X-band dual-polarization radar (XPOL) of National Observatory of Athens for the International ${\mathrm{H}}_2\mathrm{O}$ Project (IHOP) [6], the X-band polarimetric radar network (X-NET) in the Tokyo metropolitan area of Japan [7], and the X-band dual-polarization radar of the Korea Institute of Civil Engineering and Building Technology (KICT) for the urban rainfall observation [8]. To this end, an X-band dual-polarization weather radar (XPRAD) was deployed in Xinfeng County (Shaoguan, China) to play a gap-filling role, and it is the first X-band polarization radar for the SCMREX field campaign. The XPRAD radar has the capability of providing high-resolution rainfall observations within the CINRAD operational radar coverage. The adaptive scanning strategy of the XPRAD radar also increases its operability to fast-moving mesoscale convective systems.

However, reflectivity ($Z_h$) and differential reflectivity ($Z_{dr}$) measured by X-band radar are attenuated by heavy rain and supposed to be limited for heavy rainfall observations. $Z_h$ and $Z_{dr}$ should be corrected for attenuation before use for quantitative applications such as QPE. Although there is no standard algorithm to adopt for attenuation correction, the differential propagation phase (${\mathsf{\Phi }}_{dp}$) based approach has been fairly successful in recent years. Testud et al. [9] proposed a method termed as ‘ZPHI’ to correct rainfall reflectivity profile with ${\mathsf{\Phi }}_{dp}$ constraint for space-borne radar. Matrosov et al. [10] calculated the total attenuation for $Z_h$ and $Z_{dr}$ with a fixed linear dependence on ${\mathsf{\Phi }}_{dp}$. In addition, the specific differential phase ($K_{dp}$) based rainfall relations are commonly used at higher frequencies such as the X and Ku band [11], since they are insensitive to radar calibration, partial beam blockage, rainfall attenuation, and hail contamination, moreover, $K_{dp}$ has an approximate linear relation with rainfall rate. The self-consistency of dual-polarization observations also shows that $K_{dp}$ can be used to estimate the specific attenuation at horizontal polarization ($A_h$) and specific differential attenuation ($A_{dp}$) [12,13]. Gorgucci et al. [14] present a self-consistent iterative scheme which can be directly applied to an entire radar ray. In order to improve the accuracy of the $A_h$ and $A_{dp}$ parameterized from dual-polarization measurements, Kalogiros et al. [15] enhanced the self-consistent iterative scheme using parameterization functions with a minimum parameterization error of $A_h$ and $A_{dp}$. This article utilizes the drop size distribution (DSD) data captured during SCMREX to derive the polarimetric observables with the T-matrix method at the X-band frequency [16], and regresses the nonlinear relationship of $A_h-K_{dp}$ and $A_{dp}-A_h$.

Before applying any rainfall estimate algorithm, system bias errors in $Z_h$ and $Z_{dr}$ must be evaluated. System biases in $Z_h$ and $Z_{dr}$ are often caused by the difficulty of precisely calibrating the radar hardware and its time variability during operation. The accuracy of 1 dB and 0.2 dB for $Z_h$ and $Z_{dr}$ are required, respectively [17]. There are several methods to identify the bias of $Z_{dr}$ and $Z_h$. The $Z_{dr}$ of raindrops with a diameter size less than 0.5 mm is ideally equal to zero dB, due to the spherical shape of tiny drops, which can be applied to regular volume radar data from a low elevation angle [18] (hereafter referred to as the ‘light rain at low angle’ approach). The $Z_{dr}$ of dry aggregated snow above the melting layer is less than 0.2 dB at the 60° elevation, which can be used as the expected value for calibrating [17] (hereafter referred to as the ‘dry aggregated snow’ approach). Kalogiros et al. [15] determined $Z_h$ bias through comparison with X-band reflectivity values calculated from comparison with the disdrometer data at low rain-path attenuation. The systematic bias of $Z_h$ also can be evaluated based on the self-consistency principle [19]. It is demonstrated that the rainfall estimated by $Z_h$ and $Z_{dr}$ should be the same as that estimated by the unbiased variable of $K_{dp}$ when measurements are not affected by bias [20]. The bias in the $Z_h$ can be confirmed by comparing the reconstructed $K_{dpc}$ from $Z_h$ and $Z_{dr}$ with the radar estimated $K_{dp}$ [18]. This study applies the self-consistency principle to correcting the system errors of $Z_h$, upon the completion of attenuation correction and $Z_{dr}$ systematic bias correction.

In order to evaluate the observation and performance of the XPRAD radar, scross-validations with S-band radars and rain gauges are performed. There are two S-band radars near the XPRAD radar. This is performed to compare reflectivity from the common radial coverage between the XPRAD and S-band radar to verify the composite effectivity of attenuation correction and bias assessment. Cross-validation with rain gauge observations and S-band radar rainfall estimation aims to assess the performance of the XPRAD-based QPE. Therefore, the $R(K_{dp})$ and $R\left(Z_h,Z_{dr}\right)$ as the relationships between the rainfall rate and polarized variables are used to estimate rainfall accumulation and compare with rain gauge observations and S-band radar rainfall estimation.

The paper is organized as follows. In Section 2, an overview of the XPRAD radar system and observations during SCMREX is provided. Validation of the attenuation correction and systematic bias assessment are discussed in Section 3. Performance evaluations of the rainfall estimate are presented in Section 4. The main findings of this paper are summarized in Section 5.

2. System Description and Deployment during SCMREX

The field campaign of SCMREX aims to capture composite high spatiotemporal resolution observations to detect the atmospheric environment and internal fine structures of the storm during the pre-summer rainy season in southern China. As a part of the whole composite observing network, the XPRAD radar is deployed in Xinfeng County and mainly observes the atmospheric evolution at the south of the radar where heavy rain belts occur during the pre-summer season. There are two S-band radars near the XPRAD radar, one is located in Guangzhou City (Site No. 9200), and the other is located in Heyuan City (Site No. 9672). In order to obtain the rainfall rate retrieval algorithms for XPRAD, one autonomous parsivel (particle size and velocity) unit (APU) was deployed at the Longmen national meteorological station and DSD measurements from the APU were used to simulate the rainfall rate and dual-polarization radar measurements. Within the 80 km detection range of XPRAD, there are six national-level meteorological stations where the rain gauges are well-maintained and provide ground validation of radar-based rainfall estimates.

Figure 1 shows the layout of the XPRAD radar, the S-band radars, APU and rain gauges.

Table 1. System characteristics of the XPRAD radar.

Item	Value
Wavelength	X
Antenna Diameter/m	2.4
Antenna Gain/dBi	44
3 dB Beam width/°	0.95
Polarized mode	Simultaneous Horizontal and Vertical Polarization (SHV)
Transmitted Peak Power/W	200
Bandwidth/mHz	2
Noise Figure/dB	4
Dynamic Range/dB	95
Base Data	$Z_h,\mathrm{V},\mathrm{W},Z_{dr},{\rho }_{hv},{\mathsf{\Phi }}_{dp}$
Altitude above sea level	874 m

shows the performance specifications for the XPRAD radar.

The intensive observation period (IOP) of the XPRAD radar lasted from 15 May to 15 June in 2016; the radar observations for fifteen rainfall events during IOP were captured. Detailed information about the rain events can be found in

Table 2. Rainfall events list observed by XPRAD during intensive observation period (IOP) in pre-summer season.

No.	Date	Duration Time (BJT, UTC + 8:00)	Rainfall Basic Characteristic	Evolving Direction
				From	To
1	20 May 2016	00:00–24:00	Stratiform	Southwest	Northeast
2	21 May 2016	00:00–13:00	Convective	Southwest	Northeast
3	28 May 2016	00:00–24:00	stratiform	South	North
4	29 May 2016	00:00–24:00	Convective	Southwest	Northeast
5	03 June 2016	10:30–24:00	stratiform	West	East
6	04 June 2016	00:00–24:00	stratiform	West	East
7	05 June 2016	03:00–12:21	Convective	West	East
8	08 June 2016	02:00–15:50	Convective	Southwest	Northeast
9	09 June 2016	12:57–24:00	Convective	South	North
10	10 June 2016	00:00–10:30	Convective	South	North
11	11 June 2016	02:00–24:00	Convective	Southwest	Northeast
12	12 June 2016	00:00–24:00	Convective	Northwest	Southeast
13	13 June 2016	00:00–24:00	Stratiform	West	East
14	14 June 2016	00:00–24:00	Convective	West	East
15	16 June 2016	01:30–14:30	stratiform	Southwest	Northeast

.

3. Attenuation Correction and Bias Assessment

3.1. Raindrop Model and Polarimetric Radar Observables Simulation

The performance of XPRAD was evaluated with three parts as: attenuation, systematic bias and rainfall estimation. The main procedure was performed as shown in the Figure 2. The self-consistency approach for attenuation correction and bias assessment requires several empirical relationships related to polarization variables, such as: $A_h\left(K_{dp}\right)$, $A_{dp}\left(A_h\right)$, and $K_{dp}\left(Z_h,Z_{dr}\right)$, and these relationships are sensitive to changes in DSD, drop shape and temperature, etc. Rainfall estimators including $R\left(K_{dp}\right)$, $R\left(Z_h\right)$, and $R\left(Z_h,Z_{dr}\right)$ were also simulated and used to evaluate the QPE performance. Therefore, radar observables and some factors determining the derivation of those relations are briefly described here.

Microphysical property of rain medium can be represented by the drop size distribution. A good knowledge of DSD is a prerequisite for deriving radar observables, specific attenuation and rainfall algorithms. In general, a water-content-normalized gamma DSD model can adequately account for the natural variations in the shape of rainfall DSD [9,19]:

$$N\left(D\right)=N_{w}f\left(\mu \right){\left(\frac{D}{D_0}\right)}^{\mu }\exp \left[-\left(3.67+\mu \right)\frac{D}{D_0}\right]$$

(1)

$$f\left(\mu \right)=\frac{6}{{\left(3.67\right)}^4}\frac{{\left(3.67+\mu \right)}^{\mu +4}}{\mathsf{\Gamma }\left(\mu +4\right)}$$

(2)

where $N\left(D\right)$ is the number of raindrops per unit volume per unit size interval, $D$ is the volume equivalent spherical diameter in the unit of mm, $D_0$ is the median volume diameter, $\mu$ is a distribution shape parameter, and $N_w$ is the normalized intercept parameter of an equivalent exponential distribution with the same water content and $D_0$. In this study, DSD measured by APU are used to derive the relations among the polarimetric variables. The raindrop spectra were collected every minute during the IOP and quality control procedures were first applied to check the raindrop spectra before simulation, as follows: raindrop spectra were discarded if the number of channels with nonzero counts was less than six, the rainfall rates observed by APU were less than 0.1 mm/h. In addition, raindrop spectra were integrated over 3 min intervals to represent the average status of the radar’s sampling volume [6]. A total of 5880 raindrop spectra were valid for rainfall events and then used to estimate the parameters of a normalized gamma DSD model.

The rain drop shape model (axis ratios) used in the study is a composite relation of the Andsager et al. fit for $0.11\mathrm{cm}\le D\le 0.44\mathrm{cm}$ [21], and the Beard and Chuang model for $D<0.11\mathrm{cm},D>0.44\mathrm{cm}$ [22], defined as:

$$\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$b$}\right.=\{\begin{array}{c}1.0048+0.0057D-2.628D^2+3.682D^2-1.677D^4\\ 1.012-0.144D-1.03D^2\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}D<0.11 \mathrm{cm},D>0.44 \mathrm{cm}\\ 0.11 \mathrm{cm}\le D\le 0.44 \mathrm{cm}\end{array}$$

(3)

form of DSD. Specific differential phase $K_{dp}$ can be expressed as:

$$K_{dp}=\frac{180\lambda }{\pi }\mathrm{Re}{\displaystyle \int \left[f_h\left(D\right)-f_v(D)\right]}N\left(D\right)dD$$

(4)

where λ is the radar wavelength; $f_h$ and $f_v$ are the complex forward-scatter amplitudes at horizontal and vertical polarizations, respectively. The two-way differential propagation phase ${\mathsf{\Phi }}_{dp}$ is described as:

$${\mathsf{\Phi }}_{dp}=2{\displaystyle \int K_{dp}\left(r\right)}dr$$

(5)

The measured differential propagation phase is expressed as:

$${\mathsf{\Psi }}_{dp}={\mathsf{\Phi }}_{dp}+{\delta }_{hv}$$

(6)

where ${\mathsf{\Psi }}_{dp}$ is the total differential phase and can be estimated from copolar covariance, ${\delta }_{hv}$ is the backscattering propagation phase.

The reflectivity factors $Z_{h,v}$ at horizontal and vertical polarizations are defined as:

$$Z_{h,v}\left(\mathrm{dBz}\right){=10\log }_{10}\left[\frac{{\lambda }^4}{{\pi }^5{\left|K_w\right|}^2}{\displaystyle \int {\sigma }_{h,v}\left(D\right)N\left(D\right)dD}\right]$$

(7)

where ${\sigma }_h$ and ${\sigma }_v$ are the radar cross-section at horizontal and vertical polarization, respectively; $K_w$ is the dielectric factor of water given by $K_w=\left({\epsilon }_r-1\right)/\left({\epsilon }_r+2\right)$, here ${\epsilon }_r$ is the complex dielectric constant of water. Differential reflectivity $Z_{dr}$ is defined as the ratio of reflectivity factor at horizontal and vertical polarizations:

$$Z_{dr}\left(\mathrm{dB}\right)=10{\log }_{10}\left[\frac{{\displaystyle \int {\sigma }_h\left(D\right)N\left(D\right)dD}}{{\displaystyle \int {\sigma }_v\left(D\right)N\left(D\right)dD}}\right]$$

(8)

Specific attenuation at the horizontal and vertical polarization and differential attenuation are defined in the integral form of DSD as

$$A_{h,v}=4.343\times {10}^{-3}\mathrm{Im}{\displaystyle \int f_{h,v}\left(D\right)N\left(D\right)dD}$$

(9)

$$A_{dp}=A_h-A_v$$

(10)

where $A_{h,v}$ and $A_{dp}$ in the unite of ${\mathrm{dB}\mathrm{km}}^{-1}$.

The scattering simulations for this study were performed with the T-matrix approach [23] and in-site raindrop spectra obtained from APU, and the following conditions were considered for simulations: the wavelength of XPRAD and CINRAD, average atmosphere temperature at 28 °C, the axis ratio model defined in Equation (3), a Gaussian canting angle distribution with zero mean and the standard deviation of 10° [24], an 8-mm maximum drop diameter.

3.2. Specific Differential Phase-Based Attenuation Correction

At X-band, the attenuation of signals due to scatter and absorption by the raindrops limits the accuracy of power measurements of radars. In rain, the amount of attenuation depends on the drop size distribution (DSD), the raindrop’s extinction cross-section and atmosphere temperature. Due to its cumulative propagation effect, attenuation results in the fading of the reflectivity ($Z_h$) and differential reflectivity ($Z_{dr}$). Once $A_h$ and $A_{dp}$ are determined as a function of range, the attenuation correction of $Z_h$ and $Z_{dr}$ at a given range can be easily accomplished, respectively. The attenuated $Z_{hm}$ and $Z_{drm}$ are related to the corrected $Z_h$ and $Z_{dr}$, defined as below:

$$Z_{hm}\left(r\right)=Z_h\left(r\right)-2\underset{0}{\overset{r}{{\displaystyle \int }}}{A}_h\left(s\right)ds$$

(11)

$$Z_{drm}\left(r\right)=Z_{dr}\left(r\right)-2\underset{0}{\overset{r}{{\displaystyle \int }}}{A}_{dp}\left(s\right)ds$$

(12)

$A_h$ and $A_{dp}$ can be determined with an empirical relationship based on $K_{dp}$ under scattering constraints, defined as:

$$A_h=a{K}_{dp}^{\beta }$$

(13)

$$A_{dp}=\gamma A_h^{\rho }$$

(14)

It is worthwhile noting that the exponent $\beta$ and $\rho$ are close to unity, and the linearity has a good approximation at frequencies from 2.8 to 9.3 GHz [25,26]. Due to the variation of raindrop shape, the coefficient $\alpha$ varies from 0.139 to 0.335 dB/deg and the coefficient $\gamma$ also varies from 0.114 to 0.174 dB/deg. The variation differences of $\beta$ or $\rho$ influenced by temperature is much smaller than that of coefficient $\alpha$ or $\gamma$. The uncertainty of $\alpha$ and $\gamma$ accounts for 28% or 17% relative errors to the mean value respectively [12]. The simulations for $A_h-K_{dp}$ and $A_{dp}-A_h$ were performed as shown in the scatterplot of Figure 3. Through nonlinear regression processing, $\alpha$ and $\gamma$ here are 0.323 and 0.131, $\beta$ and $\rho$ are 1.05 and 1.2, as shown in

Table 3. Coefficients for the relations of $A_h\left(K_{dp}\right)$ , $A_{dp}\left(A_h\right)$, and $K_{dp}\left(Z_h,Z_{dr}\right)$, at X-band. These polarimetric observables are simulated by T-matrix calculation.

${\mathit{A}}_{\mathit{h}}=\mathit{\alpha }{\mathit{K}}_{\mathit{d}\mathit{p}}^{\mathit{\beta }}$		${\mathit{A}}_{\mathit{d}\mathit{p}}=\mathit{\gamma }{\mathit{A}}_{\mathit{h}}^{\mathit{\rho }}$		${\mathit{K}}_{\mathit{d}\mathit{p}}=\mathit{a}{\mathit{Z}}_{\mathit{h}}^{\mathit{b}}{\mathit{Z}}_{\mathit{d}\mathit{r}}^{\mathit{c}}$
$\alpha$	$\beta$	$\gamma$	$\rho$	$a$	$b$	$c$
0.323	1.05	0.131	1.2	$2.22\times {10}^{-4}$	1	−4.58

. The correlation coefficient between $A_h$ and $K_{dp}$, $A_{dp}$ and $A_h$ is 0.99 and 0.96, respectively, and indicates that the empirical relations are eligible for attenuation correction at the X band, based on the self-consistent method.

In order to evaluate the attenuation correction performance, fifteen precipitation events during IOP were chosen to accomplish the $K_{dp}$ retrieval and attenuation correction of $Z_h$ and $Z_{dr}$. Figure 4 shows a storm example case occurred at 11:57 (BJT: time of Beijing, UTC + 8:00) on 5 June 2016, including corrected polarimetric variables observed by XPRAD and reflectivity observed by the two nearest S-band CINRAD (9200 and 9762). In the $K_{dp}$ image (Figure 4b), a strong echo with a high $K_{dp}$ above 3° km⁻¹ occurred in the region marked with ‘A’ where high reflectivity were also observed by two S-band radars (Figure 4g,h), while the corresponding reflectivity observed by XPRAD (Figure 4e) is relatively lower. The overall differential reflectivity observed by XPRAD is impacted by attenuation and systematic bias that causes underestimation in region A. Figure 4d and f show corrected $Z_h$ and $Z_{dr}$ images obtained from the correction algorithm for rain attenuation. Compared to the Figure 4e, the weak reflectivity in region A shown in Figure 4f has now been increased up to 35 dBZ above, owing to the attenuation correction. These corrected $Z_h$ values are now similar to those observed by the S-band radar and are in good consistency with the $K_{dp}$. The measured large $Z_{dr}$ values in Figure 4c have also been corrected, authentic light rainfall has approximated zero dB of $Z_{dr}$. Thus, the $Z_h$ and $Z_{dr}$ after correction are consistent with the $K_{dp}$ pattern (Figure 4b), which is not affected by attenuation.

Furthermore, to validate the overall performance of attenuation correction, the scattergram comparisons of $K_{dp}$ versus $Z_h$, $Z_{dr}$ versus $Z_h$, and $K_{dp}/Z_{hl}$ ($Z_{hl}$ is in the linear unit of mm⁶m⁻³) versus $Z_{dr}$ for all fifteen rainfall events at LongMen station are performed to investigate the efficiency of attenuation correction (see Figure 5). The comparisons with the attenuation uncorrected $Z_h$ and $Z_{dr}$ values are presented in the left panels, while the right panels are for the attenuation corrected values. The radar data points in the figures are from the PPI at the elevation angle of 0.5° of rainfall events. The black asterisks along with the colored density scatters are the simulated radar moments using raindrop spectra data. It is shown in Figure 5a that, for a given $K_{dp}$, the uncorrected $Z_h$ values are much smaller than those expected from the corrected $K_{dp}$–$Z_h$ relations (Figure 5b). Similar patterns are also observed in the comparisons of $Z_{dr}$ versus $Z_h$ (Figure 5c,d) and $K_{dp}/Z_{hl}$ versus $Z_{dr}$ (Figure 5e,f). Figure 5d also shows that the bias of $Z_{dr}$ exists as light $Z_h$ ranging from 5 to 15 dBZ corresponding to a non–zero mean value of $Z_{dr}$, which did not qualify well the principle of ‘light rain at low angle’. The existence of a tiny bias is normal, since the balance of two channels may vary along time. Compared with the DSD-simulated radar moments, the XPRAD radar observations visually keep the consistency with the theoretical simulation.

3.3. Assessment of $Z_{dr}$ and $Z_h$ Measurement Biases

3.3.1. $Z_{dr}$ Bias Assessment

The gain and loss differences between the horizontal and vertical channel induce systematic bias in the $Z_{dr}$ estimate. The accuracy of $Z_{dr}$ with 0.2 dB is required for the application of QPE or hydrometeor classification [17] and self-consistency process, therefore, careful absolute calibration is necessary. The two methods for $Z_{dr}$ bias correction are employed here considering the respective strengths and limitations.

Light rain at low angle (LRLA). The shape of large-sized free-falling rain drops are modeled as non-spherical oblate spheroids [22]. This is the result of forces and surface tension acting around the drops. Moreover, rain drops with a diameter size less than 0.5 mm can be modeled using a nearly spherical shape. This inherent microphysical property of small drops can be used to estimate the $Z_{dr}$ bias. Due to the spherical shape of small drops (raindrop axis ratio ≈ 1), the power return from both polarizations (horizontal and vertical) is expected to be identical. This will lead to an expected measured mean $Z_{dr}$ of approximately 0 dB plus/minus the estimated radar measurement bias. The mean $Z_{dr}$ was estimated only using the pixels with ${\rho }_{hv}$ greater than 0.95, SNR greater than 10 dB $Z_h$ ranging from 10 to 15 dBZ. Besides, rainfall over the radome can induce signal attenuation and lead to the uncertainty of bias estimation. The data at times without rain over the radar radome were selected for assessing the systematic bias. Figure 6 shows an example scatter of $Z_h$ versus $Z_{dr}$ captured at 1.5° elevation angle of one rainfall event at 16:25 (BJT) on 4 June 2016. It can be seen from the plot that the mean $Z_{dr}$ increases exponentially with $Z_h$. For this case, the average bias is 0.481 dB.

Dry aggregated snow (DAS). The average $Z_{dr}$ values of aggregated snow normally do not exceed 0.25 dB and tend to slowly decrease with increasing $Z_h$ [17]. Considering the low variability of the expected power returns from dry aggregated snowflakes between the S- and X-band, the estimated value of 0.2 dB accounts for the absolute calibration of $Z_{dr}$ at X-band [18]. Dry aggregated snowflakes are universally present above the melting layer in stratiform clouds. The existence and identification of bright bands becomes the prerequisite for calibration using ‘dry aggregated snow’ method. A number of polarimetric observations show that the aggregated snow likely occurs around 1–2 km above the bright band [27]. Figure 7 represents a vertical profile example case of $Z_h$, $Z_{dr}$, and ${\rho }_{hv}$ from the stratiform precipitaon at 16:25 (BJT) on 4 June 2016. ${\rho }_{hv}$ is the main polarized variable which can be used to identify the melting layer and freezing-level heights, and discriminating among rain, snow, and melting-level regions. The magnitude of ${\rho }_{hv}$ is generally in the range of 0.7 to 0.95 in the melting layer. For this case, a ${\rho }_{hv}$ lower than 0.8 was observed at the melting layer where the height is 3.3 km. Upon this, the average value $Z_{dr}$ at the height between 4.3 and 5.3 km was approximate to the systematic bias, which is about 0.52 dB and nearly equal to that estimated by the ‘light rain at low angle’ approach for the same case.

Two approaches were applied for the whole rainfall event to estimate daily $Z_{dr}$ bias. The ‘light rain at low angle’ approach was eligible for all of the rainfall events. The ‘dry aggregated snow’ approach was performed only for the stratiform rainfall event, considering that dry snow is hardly identified for convective rainfall. There were six stratiform rainfall processes for fifteen rainfall events.

Table 4. Mean and standard deviation of $Z_{dr}$ bias estimated by the DAS ¹ and LRLA ² approaches for all rainfall events.

Rainfall Event No.	Mean of ${\mathit{Z}}_{\mathit{d}\mathit{r}}$ Bias (dB)		Standard Deviation of ${\mathit{Z}}_{\mathit{d}\mathit{r}}$ Bias (dB)
	DAS Approach	LRLA Approch	DAS Approach	LRLA Approch
1	0.52	0.43	0.13	0.18
2	—	0.48	—	0.17
3	0.75	0.52	0.15	0.19
4	—	0.53	—	0.21
5	0.65	0.65	0.16	0.21
6	0.63	0.65	0.15	0.30
7	—	0.61	—	0.20
8	—	0.60	—	0.25
9	—	0.68	—	0.17
10	—	0.69	—	0.18
11	—	0.76	—	0.24
12	—	0.75	—	0.22
13	0.79	0.78	0.22	0.21
14	—	0.79	—	0.22
15	0.77	0.81	0.21	0.32

¹ DAS is the acronym of ‘dry aggregated snow’. ² LRLA is the acronym of ‘light rain at low angle’.

shows the mean and standard deviation of the $Z_{dr}$ bias estimated by the DAS and LRLA approaches for all rainfall events.

Several characteristic of $Z_{dr}$ bias over IOP can be found from Table 4, such as: (1) The mean of the $Z_{dr}$ bias estimated by the ‘dry aggregated snow’ approach and the ‘light rain at low angle’ approach varied from 0.52 dB to 0.79 dB, and from 0.43 dB to 0.81dB, respectively, The standard deviation of $Z_{dr}$ bias estimated by the ‘dry aggregated snow’ approach and the ‘light rain at low angle’ approach varied from 0.13 dB to 0.22 dB, and from 0.17 to 0.32 dB, respectively; (2) The changing trend of $Z_{dr}$ bias can be seen as slightly increasing from both approaches.; (3) The ‘dry aggregated snow’ approach has a lower estimate standard deviation than the ‘light rain at low angle’ approach; (4) The overall average of $Z_{dr}$ bias is 0.68 dB and 0.65 dB, respectively, for the DAS and LRLA approach.

Based on the quantitative bias assessment, the biased $Z_{dr}$ can be corrected as:

$$Z_{dr}=Z_{drm}-Z_{dr(bias)}$$

(15)

where $Z_{drm}$ is measured differential reflectivity, $Z_{dr\left(bias\right)}$ is averaged bias for each event, and bias correction was performed with separate $Z_{dr\left(bias\right)}$ for each rainfall event.

3.3.2. $Z_h$ Bias Assessment

The self-consistency principle claim that the polarimetric variables of $Z_h$, $Z_{dr}$ and $K_{dp}$ lie in a limited 3-D space for rain medium [20]. As such, $K_{dpc}$ measurements can be reconstructed from $Z_h$ and $Z_{dr}$ measurements, as defined below.

$$K_{dpc}=a{Z}_{hl}^b{Z}_{drl}^c$$

(16)

where $K_{dpc}$ represents the specific differential phase reconstructed from $Z_h$ and $Z_{dr}$, $Z_{hl}$ and $Z_{drl}$ are in linear units. Before reconstruction, $Z_{dr}$ is corrected for attenuation and bias, and $Z_{dr}$ is corrected for attenuation. Two methods were evaluated for $Z_{dr}$ bias correction: the intrinsic properties of dry aggregated snow present above the melting layer, and light rain measurements close to the ground. The parameters a, b, and c depend on the size, shape, and distribution of raindrops and can be calculated using rain simulations with a gamma DSD and a fixed drop axis ratio relationship. The bias $Z_{h(bais)}$ in $Z_h$ can be obtained using the following relationship:

$$Z_{h(bias)}=\frac{10}{b}\mathrm{lo}{\text{g}}_{10}\left(\frac{K_{dpm}}{K_{dpc}}\right)$$

(17)

where $K_{dpm}$ is the computed specific differential phase obtained from the measured radar differential phase.

The self-consistency principle was applied for the fifteen rainfall events. Based on the radar variables simulated from the in-site raindrop spectra data, the parameters a, b, and c were regressed as 2.22 × 10⁻⁴, 1, and −4.58, respectively, shown in It is worthwhile noting that the exponent $\mathsf{\beta }$ and $\mathsf{\rho }$ are close to unity, and the linearity has a good approximation at frequencies from 2.8 to 9.3 GHz [25,26]. Due to the variation of raindrop shape, the coefficient $\mathsf{\alpha }$ varies from 0.139 to 0.335 dB/deg and the coefficient $\mathsf{\gamma }$ also varies from 0.114 to 0.174 dB/deg. The variation differences of $\mathsf{\beta }$ or $\mathsf{\rho }$ influenced by temperature is much smaller than that of coefficient $\mathsf{\alpha }$ or $\mathsf{\gamma }$. The uncertainty of $\mathsf{\alpha }$ and $\mathsf{\gamma }$ accounts for 28% or 17% relative errors to the mean value respectively [12]. The simulations for ${\mathrm{A}}_{\mathrm{h}}-{\mathrm{K}}_{\mathrm{dp}}$ and ${\mathrm{A}}_{\mathrm{dp}}-{\mathrm{A}}_{\mathrm{h}}$ were performed as shown in the scatterplot of Figure 3. Through nonlinear regression processing, $\mathsf{\alpha }$ and $\mathsf{\gamma }$ here are 0.323 and 0.131, $\mathsf{\beta }$ and $\mathsf{\rho }$ are 1.05 and 1.2, as shown in Table 3. The correlation coefficient between ${\mathrm{A}}_{\mathrm{h}}$ and ${\mathrm{K}}_{\mathrm{dp}}$, ${\mathrm{A}}_{\mathrm{dp}}$ and ${\mathrm{A}}_{\mathrm{h}}$ is 0.99 and 0.96, respectively, and indicates that the empirical relations are eligible for attenuation correction at the X band, based on the self-consistent method.

With the attenuation and bias corrected $Z_{dr}$ and retrieved $K_{dp}$, the $Z_h$ bias assessment using the self-consistency principle was performed for rainfall events. In order to validate the efficiency of self-consistency-based bias assessment, it was performed to compare XPRAD and the two closest S-band CINRAD radars (9200 and 9762) that were supposed to be well-calibrated. To perform the X-band and S-band data comparison, scatter plots of $Z_S$ ($Z_h$ from S-band) versus $Z_X$ ($Z_h$ from X-band) were generated for the same radial direction at the elevation of 0.5°, shown as Figure 8a,b. Terrain height changing between the X- and S-band radar is also considered with the usage of the DEM (digital elevation model) data, shown as green color padding in Figure 8a,b. There is some slight terrain blockage for CINRAD (9200) at the azimuth of 35°. The beam blockage ratio (BBR) was calculated with the method described in [28]. The BBR along this radial varies from 0.03 to 0.24, and the reflectivity was compensated with the BBR calculation.

For radar data selection, only 0.5° PPI scans with a data collection time difference of less than 1 min were selected. Pixels where both the S- and X-band data coexist within a $Z_h$ value in the range of 15 dBZ to 45 dBZ were selected to limit the errors due to uncertainty in low $Z_h$ returns and the deviation from Rayleigh scattering of big drops from high $Z_h$ returns in the X-band data. Figure 8a,b shows the common radial coverage area at the elevation of 0.5° between the S-band radar and the X-band radar along the same radial direction. The S-band range bin length was 250 m, the X-band range bin length was 75 m. The common range bin step was 750 m. Within the common radial range, the reflectivity at every 750 m interval for the common coverage of both radar was selected. After the data pixel selection was performed, the mean $Z_S$ and mean $Z_X$ values were computed for each radar separately for all the available reflectivity values from the PPI scan at the elevation of 0.5°.

To estimate the reflectivity bias between the CINRAD and XPRAD, the following statistical approach was used:

$$\Delta Z=\frac{1}{n}{{\displaystyle \sum }}^{}\left(Z_S-Z_X\right)$$

(18)

where n represents the number of $Z_h$ meeting the selection condition for each radar throughout each rainfall event, $Z_X$ is the reflectivity from XPRAD and just corrected for attenuation prior to bias correction with self-consistency processing, $Z_s$ is the reflectivity from CINRAD.

The $Z_h$ bias estimated by the self-consistency approach and the two closest CINRAD are shown in

Table 5. Mean and standard deviation of $Z_h$ bias by the self-consistency approach and the two closest CINRAD.

Rainfall Event No.	Mean of ${\mathit{Z}}_{\mathit{h}}$ Bias (dB)			Standard Deviation of ${\mathit{Z}}_{\mathit{h}}$ Bias (dB)
	Self-Consistency	CINRAD (9200)	CINRAD (9762)	Self-Consistency	CINRAD (9200)	CINRAD (9762)
1	0.10	0.31	1.1	0.08	0.18	0.19
2	0.19	0.33	0.15	0.12	0.24	0.15
3	0.25	0.28	0.83	0.12	0.25	0.24
4	0.14	0.95	—	0.16	0.19	—
5	0.19	0.56	0.50	0.18	0.18	0.24
6	0.93	1.23	1.41	0.33	0.48	0.18
7	0.97	0.78	0.69	0.38	0.32	0.23
8	0.96	0.98	0.48	0.38	0.37	0.19
9	0.96	0.11	0.74	0.37	0.24	0.20
10	1.38	—	—	0.39	—	—
11	1.05	—	—	0.37	—	—
12	0.61	0.72	0.96	0.12	0.27	0.38
13	0.39	0.30	0.28	0.21	0.36	0.20
14	0.40	—	0.76	0.20	—	0.12
15	0.35	1.25	1.1	0.19	0.26	0.13

. There are no comparison outcomes between CINRAD and XPRAD for rainfall event number 4, 10, 11 and 14, since the corresponding rainfall event did not occur at the common radial coverage. The $Z_h$ bias estimated by the self-consistency approach, CINRAD (9200) and CINRAD (9762) varies from 0.10 dBZ to 1.38 dBZ, from 0.11 dBZ to 1.23 dBZ, and from 0.15 dBZ to 1.41 dBZ, respectively. The overall average $Z_h$ bias estimated by the self-consistency approach, CINRAD (9200) and CINRAD (9762) is 0.60 dBZ, 0.65 dBZ, and 0.75 dBZ, respectively. The maximum $Z_h$ bias estimated is 1.41 dBZ, less than 1.5 dBZ. The maximum standard deviation of $Z_h$ bias estimated is 0.48 dBZ, less than 0.5 dBZ. Such small differences demonstrate the feasibility of the application of the self-consistency criterion in a dual polarization radar measurement quality check.

Based on the quantitative assessment, the biased $Z_h$ can be corrected with a self-consistency estimation, as:

$$Z_h=Z_{hm}+Z_{h(bais)}$$

(19)

where $Z_{hm}$ is the measured reflectivity, $Z_{dr\left(bias\right)}$ is the averaged bias for each event, and bias correction was performed with a separate $Z_{dr\left(bias\right)}$ for each rainfall event.

4. Rainfall Performance during SCMREX

4.1. Rainfall Algorithms

Based on the physical principle of precipitation, the rainfall rate can be represented by DSD density, defined as:

$$R=0.6\pi \times {10}^{-3}{\displaystyle \int v\left(D\right)}{D}^{3}N\left(D\right)dD$$

(20)

where $v\left(D\right)$ is the raindrop terminal velocity in the unit of $\text{m}{\text{s}}^{-1}$, D is the raindrop diameter in mm, $N\left(D\right)$ is the DSD density in the unit of ${\text{m}}^{-3}\text{m}{\text{m}}^{-1}$.

For a given DSD dataset, a variety of empirical rainfall relationships between the polarimetric variables and rainfall rate can be derived via nonlinear regression. In this study, $R\left(Z_h,Z_{dr}\right)$ and $R\left(K_{dp}\right)$ were estimated to validate the self-consistency and QPE performance for XPRAD. Herein, $R\left(Z_h,Z_{dr}\right)$ is fundamentally a power-based relation, whereas $R\left(K_{dp}\right)$ is a phase-based method. Meanwhile, a CINRAD-based QPE was also performed. The relation of $R\left(Z_h\right)$ was widely adopted for CINRAD, since many CINRADs are a single horizontal polarization radar.

The rainfall rate (R) versus the $K_{dp}$, $Z_h$ and $Z_{dr}$ for the X-band are simulated from in-site raindrop spectra data based on the T-matrix approach under the simulation conditions described in Section 3.1. The scatter density plot of R versus $K_{dp}$ is drawn in Figure 9a. The best fit power law relation for R-$K_{dp}$ is regressed as shown in Figure 9a by a red line. The scatterplot of R versus $Z_h$ and $Z_{dr}$ is shown in Figure 9b by a gray square, and the best fit power law relation for R versus $Z_h,Z_{dr}$ was also regressed and is shown by the colored three-dimensional mesh. The specific parameters of the rainfall algorithms were obtained as:

$$R\left(K_{dp}\right)=15.1K_{dp}^{0.92};(\mathrm{X}-\mathrm{band})$$

(21)

$$R\left(Z_h,Z_{dr}\right)=0.009\times {10}^{\left(0.1\times Z_h-0.458\times Z_{dr}\right)};(\mathrm{X}-\mathrm{band})$$

(22)

where, $Z_h$ is in the unit of dBZ, and $Z_{dr}$ is in the unit of dB. The rainfall rate (R) versus the $Z_h$ for the S-band is also simulated from raindrop spectra data with the T-matrix method, and the best-fit power low relation to determine the coefficients for $R\left(Z_h\right)$ is regressed as shown in Figure 10. The specific parameters of the rainfall algorithms are obtained as

$$R\left(Z_h\right)=0.0216\times {10}^{\left(0.069\times Z_h\right)};(\mathrm{S}-\mathrm{band})$$

(23)

It should be noted that the relations in Equations (21)–(23) are particularly suited for the region in Guangdong province.

4.2. Performance Evaluation

In order to demonstrate the XPRAD performance for QPE, the rainfall records from a rain gauge network, which consists of six gauges, were used for evaluation purposes. The gauge network is deployed and managed by the Guangdong Meteorological Bureau. For the sake of cross comparisons, we aggregated the rainfall data to rainfall accumulations in 1.0-, 2.0- and 3.0-h intervals. The radar measurements were spatially chosen at the location of the rain gauges for validation. For the sake of quantifying the accuracy of XPRAD rainfall products, the fractional standard error (FSE), normalized mean bias (NMB) and correlation coefficient (CORR) of the rainfall amount at different time scales were computed for $R\left(Z_h,Z_{dr}\right)$, $R(K_{dp}$) and $R(Z_h$) defined as:

$$FSE=\frac{\sqrt{\frac{1}{N}{{\displaystyle \sum }}_i^N{\left({\mathrm{r}}_i-{\mathrm{g}}_i\right)}^2}}{\frac{1}{N}{{\displaystyle \sum }}_i^N{\mathrm{g}}_i}\times 100\%$$

(24)

$$NMB=\frac{\frac{1}{N}{{\displaystyle \sum }}_i^N\left({\mathrm{r}}_i-{\mathrm{g}}_i\right)}{\frac{1}{N}{{\displaystyle \sum }}_i^N{\mathrm{g}}_i}\times 100\%$$

(25)

$$CORR=\frac{{{\displaystyle \sum }}_i^N\left({\mathrm{g}}_i-\overline{\mathrm{g}}\right)\left({\mathrm{r}}_i-\overline{\mathrm{r}}\right)}{\sqrt{{{\displaystyle \sum }}_i^N{\left({\mathrm{g}}_i-\overline{\mathrm{g}}\right)}^2}\sqrt{{{\displaystyle \sum }}_i^N{\left({\mathrm{r}}_i-\overline{\mathrm{r}}\right)}^2}}$$

(26)

where FSE and NMB are in percent, CORR is dimensionless, ${\mathrm{r}}_i$ and ${\mathrm{g}}_i$ represent the rainfall accumulation from radar and gauge, N is the total sampling number.

The NMB and FSE results, as well as the mean values of the gauge rainfall measurement at different time scales (i.e., 1-, 2- and 3-h) for each of the events, are shown in

Table 6. Assessment of $R(K_{dp})$ , $R\left(Z_h,Z_{dr}\right)$ and $R(Z_h)$ for fifteen rainfall events under four scales of accumulated time interval.

Time Scale (Hour)	FSE (%)				NMB (%)				CORR
	XPRAD $\mathit{R}\left({\mathit{Z}}_{\mathit{h}},{\mathit{Z}}_{\mathit{d}\mathit{r}}\right)$	XPRAD $\mathit{R}({\mathit{K}}_{\mathit{d}\mathit{p}})$	9200 $\mathit{R}({\mathit{Z}}_{\mathit{h}})$	9762 $\mathit{R}({\mathit{Z}}_{\mathit{h}})$	XPRAD $\mathit{R}\left({\mathit{Z}}_{\mathit{h}},{\mathit{Z}}_{\mathit{d}\mathit{r}}\right)$	XPRAD $\mathit{R}({\mathit{K}}_{\mathit{d}\mathit{p}})$	9200 $\mathit{R}({\mathit{Z}}_{\mathit{h}})$	9762 $\mathit{R}({\mathit{Z}}_{\mathit{h}})$	XPRAD $\mathit{R}\left({\mathit{Z}}_{\mathit{h}},{\mathit{Z}}_{\mathit{d}\mathit{r}}\right)$	XPRAD $\mathit{R}({\mathit{K}}_{\mathit{d}\mathit{p}})$	9200 $\mathit{R}({\mathit{Z}}_{\mathit{h}})$	9762 $\mathit{R}({\mathit{Z}}_{\mathit{h}})$
1.0	71.37	79.77	69.75	72.58	−13.62	−10.65	−13.84	−11.78	0.87	0.86	0.92	0.91
2.0	68.98	57.95	60.45	51.08	−3.10	−4.84	−11.12	−4.91	0.89	0.91	0.91	0.93
3.0	62.22	50.75	52.11	41.30	0.04	−2.64	−12.55	−2.33	0.90	0.92	0.91	0.94

. In addition, the overall NMB and FSE were calculated, at each time scale, based on the entire observation combining all the fifteen events. The main findings from the evaluation results of different rainfall products are summarized as follows:

(1)

The FSEs of the $R\left(Z_h,Z_{dr}\right)$ are 71.37%, 68.98%, and 62.22% for 1-, 2- and 3-h rainfall accumulations, respectively, and the NMBs are −13.62%, −3.1%, and 0.04%, respectively. The FSEs of the $R(K_{dp})$ are 79.77%, 57.95%, 50.75%, for 1-, 2- and 3-h rainfall accumulations, respectively, and the NMBs are −10.65%, −4,84%, and −2.64%, respectively. The NMBs and FSEs of $R(K_{dp})$ estimated for XPRAD are approximate to those estimated for CINRAD. The performance is further demonstrated by the combined scatter plots shown in Figure 11.

(2)

Although the $R(K_{dp})$ shows slightly better performance than $R\left(Z_h,Z_{dr}\right)$, the difference is not remarkable. This also implies that attenuation and bias correction are critical for X-band QPE applications.

(3)

It can also be seen that the FSEs of the rainfall estimate relations show a decreasing trend as the rainfall accumulation time increases from 1 h to 3 h, inversely the CORR of the rainfall estimate relations had an increasing trend. This is because the random radar measurement errors are being reduced by temporal averaging.

5. Summary and Conclusions

Endorsed by the World Meteorological Organization (WMO) World Weather Research Program (WWRP), the China Meteorological Administration (CMA) has initiated the SCMREX field experiment to facilitate the efforts in improving QPE/QPF during the pre-summer rainy season in southern China. The X-band XPRAD radar is deployed as part of the integrated observing network of SCMREX during the intensive observation periods, aiming to fill the gaps of the operational S-band weather radar coverage and provide high resolution observations through its flexible scan strategy.

However, the X-band deployment did not come easily, as technical solutions need to be found for several issues including attenuation correction. This paper takes advantage of the dual-polarization technique, particularly the differential phase measurements that are not affected by radar calibration and attenuation, to quantitatively correct attenuation and systematic biases on $Z_h$ and $Z_{dr}$. The XPRAD radar data collected for fifteen rainfall events during the intensive observation period in 2016 were investigated to demonstrate the data quality and rainfall performance.

It is concluded that the $Z_{dr}$ bias varies within a mean value of 0.68 dB. The calibration accuracy of $Z_{dr}$ is less than 0.2 dB. Both the self-consistency-based calculation and the cross-validation between the S-band radar observations show that the $Z_h$ observed by XPRAD has a mean bias value less than 1.6 dBZ and a standard deviation less than 0.5 dBZ. The 1-, 2- and 3-h rainfall accumulations derived using R($K_{dp}$) and R($Z_h,Z_{dr}$) agree well with the rain gauge measurements and the CINRAD-based rainfall estimation, which demonstrates the good performance of the XPRAD radar for QPE. The XPRAD product evaluation showed that the R($K_{dp}$)-based algorithm had lower overall biases of −10.65%, −4,84% and −2.64%, and a higher correlation coefficient of 0.86, 0.91 and 0.92, for 1-, 2- and 3-h rainfall accumulations, respectively. It is worth noting that R($Z_h,Z_{dr}$) showed similar performance to R($K_{dp}$), if $Z_h\mathrm{and}{Z}_{dr}$ were well-corrected. The SCMREX field campaign was extended to 2018 by the WMO and future studies with XPRAD will focus on DSD retrieval and the classification of different hydrometeor types for pre-summer precipitation over southern China.