Influence of Wave State and Sea Spray on the Roughness Length: Feedback on Medicanes
Abstract
:1. Introduction
2. Materials and Methods
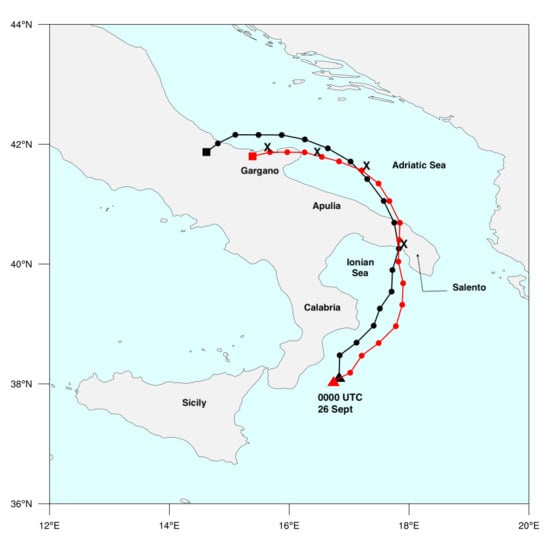
2.1. The Event: Synoptic Description
2.2. Roughness Length over the Sea Surface
2.3. Mechanisms of Sea Spray Generation under High Wind Conditions
2.4. SWAN Setup
2.5. WRF-Chem Setup
3. Results and Discussion
3.1. WRF/SWAN Coupling
3.2. Analysis of the WRF-Chem Output
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Emanuel, K. Genesis and maintenance of Mediterranean hurricanes. Adv. Geosci. 2005, 2, 217–220. [Google Scholar] [CrossRef]
- Reale, O.; Atlas, R. Tropical cyclone–like vortices in the extratropics: Observational evidence and synoptic analysis. Weather Forecast. 2001, 16, 7–34. [Google Scholar] [CrossRef]
- Tous, M.; Romero, R. Meteorological environments associated with medicane development. Int. J. Climatol. 2013, 33, 1–14. [Google Scholar] [CrossRef]
- Tous, M.; Romero, R.; Ramis, C. Surface heat fluxes influence on medicane trajectories and intensification. Atmos. Res. 2013, 123, 400–411. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Kotroni, V.; Nickovic, S.; Jovic, D.; Kallos, G. Observations and model simulations of a winter subsynoptic vortex over the central Mediterranean. Meteorol. Appl. 1999, 6, 371–383. [Google Scholar] [CrossRef]
- Moscatello, A.; Miglietta, M.M.; Rotunno, R. Numerical analysis of a Mediterranean ‘hurricane’ over southeastern Italy. Mon. Weather Rev. 2008, 136, 4373–4397. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Laviola, S.; Malvaldi, A.; Conte, D.; Levizzani, V.; Price, C. Analysis of tropical-like cyclones over the Mediterranean Sea through a combined modelling and satellite approach. Geophys. Res. Lett. 2013, 40, 2400–2405. [Google Scholar] [CrossRef]
- Pytharoulis, I. Analysis of a Mediterranean tropical-like cyclone and its sensitivity to the sea surface temperatures. Atmos. Res. 2018, 208, 167–179. [Google Scholar] [CrossRef]
- Homar, V.; Romero, R.; Stensrud, D.J.; Ramis, C.; Alonso, S. Numerical diagnosis of a small, quasi-tropical cyclone over the western Mediterranean: Dynamical vs. boundary factors. Q. J. R. Meteorol. Soc. 2003, 129, 1469–1490. [Google Scholar] [CrossRef] [Green Version]
- Cioni, G.; Malguzzi, P.; and Buzzi, A. Thermal structure and dynamical precursor of a Mediterranean tropical-like cyclone. Q. J. R. Meteorol. Soc. 2016, 142, 1757–1766. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Cerrai, D.; Laviola, S.; Cattani, E.; Levizzani, V. Potential vorticity patterns in Mediterranean “hurricanes”. Geophys. Res. Lett. 2017, 44, 2537–2545. [Google Scholar] [CrossRef]
- Cavicchia, L.; von Storch, H.; Gualdi, S. A long-term climatology of medicanes. Clim. Dyn. 2014, 43, 1183–1195. [Google Scholar] [CrossRef]
- Nastos, P.T.; Papadimou, K.K.; Matsangouras, I.T. Mediterranean tropical-like cyclones: Impacts and composite daily means and anomalies of synoptic patterns. Atmos. Res. 2018, 206, 156–166. [Google Scholar] [CrossRef]
- Hart, R.E. A cyclone phase space derived from thermal wind and thermal asymmetry. Mon. Weather Rev. 2003, 131, 585–616. [Google Scholar] [CrossRef]
- Picornell, M.A.; Campins, J.; Jansà, A. Detection and thermal description of medicanes from numerical simulation. Nat. Hazards Earth Syst. Sci. 2014, 14, 1059–1070. [Google Scholar] [CrossRef] [Green Version]
- Fita, L.; Flaounas, E. Medicanes as subtropical cyclones: The December 2005 case from the perspective of surface pressure tendency diagnostics and atmospheric water budget. Q. J. R. Meteorol Soc. 2018. [Google Scholar] [CrossRef]
- Veron, F. Ocean Spray. Annu. Rev. Fluid Mech. 2015, 47, 507–538. [Google Scholar] [CrossRef]
- Andreas, E.L.; Andreas, E.L. A review of the sea spray generation function for the open ocean. In Atmosphere-Ocean Interactions; Perrie, W.A., Ed.; WIT: Southhampton, UK, 2002; Volume 1, pp. 1–46. [Google Scholar]
- Andreas, E.L. Spray Stress Revisited. J. Phys. Oceanogr. 2004, 34, 1429–1440. [Google Scholar] [CrossRef]
- Andreas, E.L.; Persson, P.O.G.; Hare, J.E. A bulk turbulent air-sea flux algorithm for high-wind, spray conditions. J. Phys. Oceanogr. 2008, 38, 1581–1596. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Black, P.G.; D’Asaro, E.A.; Drennan, W.M.; French, J.R.; Niiler, P.P.; Sanford, T.B.; Terrill, E.J.; Walsh, E.J.; Zhang, J.A. Air-sea exchange in hurricanes: Synthesis of observations from the Coupled Boundary Layer Air-Sea Transfer Experiment. Bull. Am. Meteorol. Soc. 2007, 88, 357–374. [Google Scholar] [CrossRef]
- Donelan, M.A.; Drennan, W.M.; Katsaros, K.B. The air–sea momentum flux in conditions of wind sea and swell. J. Phys. Oceanogr. 1997, 27, 2087–2099. [Google Scholar] [CrossRef]
- Makin, V.K. A note on the drag of the sea surface at hurricane winds. Bound. Layer Meteorol. 2005, 115, 169–176. [Google Scholar] [CrossRef]
- Charnock, H. Wind Stress on Water: An Hypothesis. Q. J. R. Meteorol. Soc. 1955, 81, 320–332. [Google Scholar] [CrossRef]
- Liu, B.; Liu, H.; Xie, L.; Guan, C.; Zhao, D. A coupled atmosphere–wave–ocean modeling system: Simulation of the intensity of an idealized tropical cyclone. Mon. Weather Rev. 2011, 139, 132–152. [Google Scholar] [CrossRef]
- Liu, B.; Guan, C.; Xie, L.; Zhao, D. An investigation of the effects of wave state and sea spray on an idealized typhoon using an air–sea coupled modeling system. Adv. Atmos. Sci. 2012, 29, 391–406. [Google Scholar] [CrossRef]
- Wan, Z.-H.; Zhu, J.-B.; Sun, K.; Zhou, K. An integrated turbulent simulation and parameter modeling study on sea spray dynamics and fluxes. Ocean Eng. 2017, 130, 64–71. [Google Scholar] [CrossRef]
- Volkov, Y. The dependence on wave age. In Wind Stress over the Ocean; Jones, I.S.F., Toba, Y., Eds.; Cambridge University Press: Cambridge, UK, 2001; pp. 206–217. [Google Scholar]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a coupled ocean–atmosphere–wave–sediment transport (COAWST) modeling system. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef]
- Grell, G.A.; Peckham, S.E.; Schmitz, R.; McKeen, S.A.; Frost, G.; Skamarock, W.C.; Eder, B. Fully coupled “online” chemistry within the WRF model. Atmos. Environ. 2005, 39, 6957–6975. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions, 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Ricchi, A.; Miglietta, M.M.; Barbariol, F.; Benetazzo, A.; Bergamasco, A.; Bonaldo, D.; Cassardo, C.; Falcieri, F.M.; Modugno, G.; Russo, G.A.; et al. Sensitivity of a Mediterranean tropical-like cyclone to different model configurations and coupling strategies. Atmosphere 2017, 8, 92. [Google Scholar] [CrossRef]
- Chin, M.; Rood, R.B.; Lin, S.-J.; Muller, J.F.; Thomspon, A.M. Atmospheric sulfur cycle in the global model GOCART: Model description and global properties. J. Geophys. Res. Atmos. 2000, 105, 24671–24687. [Google Scholar] [CrossRef]
- Moscatello, A.; Miglietta, M.M.; Rotunno, R. Observational analysis of a Mediterranean ‘hurricane’ over south-eastern Italy. Weather 2008, 63, 306–311. [Google Scholar] [CrossRef] [Green Version]
- Miglietta, M.M.; Moscatello, A.; Conte, D.; Mannarini, G.; Lacorata, G.; Rotunno, R. Numerical analysis of a Mediterranean “hurricane” over south-eastern Italy: Sensitivity experiments to sea surface temperature. Atmos. Res. 2011, 101, 412–426. [Google Scholar] [CrossRef]
- Chaboureau, J.-P.; Pantillon, F.; Lambert, D.; Richard, E.; Claud, C. Tropical transition of a Mediterranean storm by jet crossing. Q. J. R. Meteorol. Soc. 2012, 138, 596–611. [Google Scholar] [CrossRef]
- Claud, C.; Alhammoud, B.; Funatsu, B.M.; Chaboureau, J.-P. Mediterranean hurricanes: Large-scale environment and convective and precipitating areas from satellite microwave observations. Nat. Hazards Earth Syst. Sci. 2010, 10, 2199–2213. [Google Scholar] [CrossRef] [Green Version]
- Conte, D.; Miglietta, M.M.; Levizzani, V. Analysis of instability indexes during the development of a Mediterranean tropical-like cyclone using MSG-SEVIRI products and the LAPS model. Atmos. Res. 2011, 101, 264–279. [Google Scholar] [CrossRef]
- Davolio, S.; Miglietta, M.M.; Moscatello, A.; Pacifico, F.; Buzzi, A.; Rotunno, R. Numerical forecast and analysis of a tropical-like cyclone in the Ionian Sea. Nat. Hazards Earth Syst. Sci. 2009, 9, 551–562. [Google Scholar] [CrossRef] [Green Version]
- Miglietta, M.M.; Mastrangelo, D.; Conte, D. Influence of physics parameterization schemes on the simulation of a tropical-like cyclone in the Mediterranean Sea. Atmos. Res. 2015, 153, 360–375. [Google Scholar] [CrossRef]
- Ricchi, A.; Miglietta, M.M.; Falco, P.P.; Bergamasco, A.; Benetazzo, A.; Bonaldo, D.; Sclavo, M.; Carniel, S. On the use of a coupled ocean-atmosphere-wave model during an extreme cold air outbreak over the Adriatic Sea. Atmos. Res. 2016, 172–173, 48–65. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N. On effect of sea droplets on atmospheric boundary layer. J. Geophys. Res. 2006, 111, C07020. [Google Scholar] [CrossRef]
- Shi, J.; Zhong, Z.; Li, R.; Li, Y.; Sha, W. Dependence of sea surface drag coefficient on wind-wave parameters. Acta Oceanol. Sin. 2011, 30, 14–24. [Google Scholar] [CrossRef]
- Tsai, Y.-S.; Chang, W.-T.; Yu, C.-M.; Yang, W.-C. General Sea State and Drag Coefficient Observed near Shore in Taiwan Strait. Procedia IUTAM 2018, 26, 204–213. [Google Scholar] [CrossRef]
- Canepa, E.; Builtjes, P.J.H. Thoughts on Earth System Modelling: From global to regional scale. Earth Sci. Rev. 2017, 171, 456–462. [Google Scholar] [CrossRef]
- Fairall, C.W.; Banner, M.L.; Peirson, W.L.; Asher, W.; Morison, R.P. Investigation of the physical scaling of sea spray spume droplet production. J. Geophys. Res. 2009, 114, C10001. [Google Scholar] [CrossRef]
- Troitskaya, Y.U.; Kandaurov, A.; Ermakova, O.; Kozlov, D.; Sergeev, D.; Zilitinkevich, S. Bag-breakup fragmentation as the dominant mechanism of sea-spray production in high winds. Sci. Rep. 2017, 7, 1614. [Google Scholar] [CrossRef] [PubMed]
- Monahan, E.C.; Spiel, D.E.; Davidson, K.L. A model of marine aerosol generation via whitecaps and wave disruption. In Oceanic Whitecaps; Springer: Dordrecht, The Netherlands, 1986; pp. 167–174. [Google Scholar]
- Zhao, D.; Toba, Y.; Sugioka, K.; Komon, S. New sea spray generation function for spume droplets. J. Geophys. Res. 2006, 111, C02007. [Google Scholar] [CrossRef]
- Holthuijse, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007; 387p. [Google Scholar]
- Oost, W.A.; Komen, G.J.; Jacobs, C.M.J.; van Oort, C. New evidence for a relation between wind stress and wave age from measurements during ASGAMAGE. Bound.-Layer Meteorol. 2002, 103, 409–438. [Google Scholar] [CrossRef]
- Mazza, E.; Ulbrich, U.; Klein, R. The tropical transition of the October 1996 medicane in the western Mediterranean Sea: A warm seclusion event. Mon. Weather Rev. 2017, 145, 2575–2595. [Google Scholar] [CrossRef]
- Komen, G.J.; Hasselmann, S.; Hasselmann, K. Existence of a fully developed wind-sea spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor–Yamada level 3 model: Its numerical stability and application to a regional prediction of advecting fog. Bound.-Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Green, B.W.; Zhang, F. Impacts of air–sea flux parameterizations on the intensity and structure of tropical cyclones. Mon. Weather Rev. 2013, 141, 2308–2324. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air–sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Dévényi, D.; Weygandt, S.S.; Brundage, K.J.; Brown, J.M.; Grell, G.A.; Kim, D.; Schwartz, B.E.; Smirnova, T.G.; Smith, T.L.; et al. An hourly assimilation–forecast cycle: The RUC. Mon. Weather Rev. 2004, 132, 495–518. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long–lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one-and two-moment schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef]
- Rizza, U.; Barnaba, F.; Miglietta, M.M.; Mangia, C.; Di Liberto, L.; Dionisi, D.; Costabile, F.; Grasso, F.; Gobbi, G.P. WRF-Chem model simulations of a dust outbreak over the central Mediterranean and comparison with multi-sensor desert dust observations. Atmos. Chem. Phys. 2017, 17, 93–115. [Google Scholar] [CrossRef] [Green Version]
- Rizza, U.; Miglietta, M.M.; Mangia, C.; Ielpo, P.; Morichetti, M.; Iachini, C.; Virgili, S.; Passerini, G. Sensitivity of WRF-Chem model to land surface schemes: Assessment in a severe dust outbreak episode in the Central Mediterranean (Apulia Region). Atmos. Res. 2018, 201, 168–180. [Google Scholar] [CrossRef]
- Wu, L.; Rutgersson, A.; Sahlée, E.; Larsén, X.G. The impact of waves and sea spray on modelling storm track and development. Tellus 2015, 67, 27967. [Google Scholar] [CrossRef] [Green Version]










| Isftcflx | z0 | (zT, zQ) |
|---|---|---|
| 0 | Fairall et al. [57] | Fairall et al. [57] |
| 5 | Liu et al. [27] | Fairall et al. [57] |
| Bins | r0min (μm) | r0max (μm) | r0eff (μm) |
|---|---|---|---|
| 1 | 10 | 30 | 20 |
| 2 | 30 | 75 | 52.5 |
| 3 | 75 | 200 | 137.5 |
| 4 | 200 | 500 | 350 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rizza, U.; Canepa, E.; Ricchi, A.; Bonaldo, D.; Carniel, S.; Morichetti, M.; Passerini, G.; Santiloni, L.; Scremin Puhales, F.; Miglietta, M.M. Influence of Wave State and Sea Spray on the Roughness Length: Feedback on Medicanes. Atmosphere 2018, 9, 301. https://doi.org/10.3390/atmos9080301
Rizza U, Canepa E, Ricchi A, Bonaldo D, Carniel S, Morichetti M, Passerini G, Santiloni L, Scremin Puhales F, Miglietta MM. Influence of Wave State and Sea Spray on the Roughness Length: Feedback on Medicanes. Atmosphere. 2018; 9(8):301. https://doi.org/10.3390/atmos9080301
Chicago/Turabian StyleRizza, Umberto, Elisa Canepa, Antonio Ricchi, Davide Bonaldo, Sandro Carniel, Mauro Morichetti, Giorgio Passerini, Laura Santiloni, Franciano Scremin Puhales, and Mario Marcello Miglietta. 2018. "Influence of Wave State and Sea Spray on the Roughness Length: Feedback on Medicanes" Atmosphere 9, no. 8: 301. https://doi.org/10.3390/atmos9080301
APA StyleRizza, U., Canepa, E., Ricchi, A., Bonaldo, D., Carniel, S., Morichetti, M., Passerini, G., Santiloni, L., Scremin Puhales, F., & Miglietta, M. M. (2018). Influence of Wave State and Sea Spray on the Roughness Length: Feedback on Medicanes. Atmosphere, 9(8), 301. https://doi.org/10.3390/atmos9080301