Using Adjacent Buoy Information to Predict Wave Heights of Typhoons Offshore of Northeastern Taiwan

Abstract

In the northeastern sea area of Taiwan, typhoon-induced long waves often cause rogue waves that endanger human lives. Therefore, having the ability to predict wave height during the typhoon period is critical. The Central Weather Bureau maintains the Longdong and Guishandao buoys in the northeastern sea area of Taiwan to conduct long-term monitoring and collect oceanographic data. However, records have often become lost and the buoys have suffered other malfunctions, causing a lack of complete information concerning wind-generated waves. The goal of the present study was to determine the feasibility of using information collected from the adjacent buoy to predict waves. In addition, the effects of various factors such as the path of a typhoon on the prediction accuracy of data from both buoys are discussed herein. This study established a prediction model, and two scenarios were used to assess the performance: Scenario 1 included information from the adjacent buoy and Scenario 2 did not. An artificial neural network was used to establish the wave height prediction model. The research results demonstrated that (1) Scenario 1 achieved superior performance with respect to absolute errors, relative errors, and efficiency coefficient (CE) compared with Scenario 2; (2) the CE of Longdong (0.802) was higher than that of Guishandao (0.565); and (3) various types of typhoon paths were observed by examining each typhoon. The present study successfully determined the feasibility of using information from the adjacent buoy to predict waves. In addition, the effects of various factors such as the path of a typhoon on the prediction accuracy of both buoys were also discussed.

1. Introduction

Taiwan is located at the border of the tropical and subtropical regions of the Pacific Ocean, where typhoons often occur during summer and autumn. Most typhoons gradually form above the sea surface southeast of Taiwan and produce torrential rains and strong winds that provide considerable water resources but also cause countrywide disasters [1]. When typhoons approach Taiwan from the Pacific Ocean, the northeastern sea and coastal area (Figure 1) are the first to be threatened. Because violent storms strike the sea surface with extreme wind speed that persists for a long duration, the resultant waves exhibit long wave periods and great wave heights [2]. Moreover, the topography of seabed may cause wave height to increase to a severely dangerous extent near the shore; for example, seawater intrusion may occur in lowland areas and anchored fishing boats may be capsized or dismantled because of the sudden rise of the waves or a fierce wave impact.

The waters near Taiwan are prone to enormous waves generated by strong winds. Such waves contain a massive amount of energy that can be transmitted to the coast of Taiwan from extremely far away, for which reason they are commonly called long waves. They can be transmitted over hundreds or thousands of kilometers, which is why in summer and autumn surface waves often suddenly occur at the east coast of Taiwan before a typhoon comes. Usually, several big waves occur in a row, after which the sea surface becomes calm for a while, and then giant waves suddenly occur again. Such a pattern gives rise to the name “rogue waves”, and locals colloquially call them “mad dog waves” [3]. Long waves move extremely fast and carry considerable momentum; long waves generated by typhoons often carry a large quantity of sea water to the coast where people often get taken under by the waves because they are caught unprepared. According to the data of the Central Weather Bureau (CWB) of Taiwan, at least 340 incidents of rogue waves were recorded between 2000 and 2018, causing injury or death to 568 persons.

Because long waves generated by typhoons often occur in the northeastern sea of Taiwan and cause rogue waves that threaten the safety of people, it is critical to develop the ability to accurately predict wave heights during a typhoon. The CWB has set up the Longdong and Guishandao buoys in the northeastern sea area (Figure 1) for long-term monitoring and the collection of key oceanographic data. The buoys record up-to-date information concerning waves in this area that can then be subjected to further analysis and used to make predictions; moreover, the information can inform public safety preparations that prevent adverse outcomes. However, performance records of the buoys indicate that there are often no wave data available owing to data loss or other malfunctions. The present study thus hypothesized that if wave heights around a particular buoy could be predicted using data from the adjacent buoy when the target buoy malfunctioned, the problems associated with buoy malfunctioning could be overcome and key information regarding the waves in the target area could still be collected [4]. The aim of this study was to evaluate the feasibility of predicting waves using the data collected by the adjacent buoy. Moreover, this study assessed the prediction accuracy of buoy data in light of the influence of various factors such as the path of typhoons. This study used two scenarios to develop the prediction model, one that used data from the adjacent buoy and one that did not. The study also evaluated other factors that might affect wave height predictions such as the path of typhoons, the location of buoys, and typhoon intensity. Artificial neural networks (ANNs) were used to develop an efficient and accurate wave prediction model.

Computation speed has increased considerably because of the rapid development of computer hardware and software. Researchers have thus been able to develop numerous wave prediction models for typhoon periods using wave theories and complex computation. Commonly used computation models include numerical models, regression analysis, and ANNs. Numerical models use wave governing equations with correction items generated from local differences to conduct complex computations. Because this method employs grid computing, the conversion from a global scale to a scale suitable for the target coast area, which involves complicated computations and grid selection, is often extremely time-consuming [5,6,7,8]. Regression analysis uses typhoon or weather parameters that affect wind waves during typhoons to establish a simple statistical regression. Then, the coefficient and intercept of each parameter on the regression line are identified to simulate the waves during a typhoon. However, whether or not a particular parameter actually affects the wave during a typhoon cannot be determined, rendering it devoid of physical meaning or implication. Key research in this field has been reported in Asma et al. [9], Li et al. [10], Makarynskyy et al. [11], Sánchez-Arcilla et al. [12], Suzuki et al. [13], and Young [14]. ANNs use the input of parameters that affect waves during a typhoon to generate outputs after performing complex statistical computations in hidden layers. By continuously computing the errors between outputs and actual measurements, this method progressively corrects the weight where connects two neurons of two adjacent layers until the output value approaches the actual measurement. For example, Mandal [15] used a deep learning ANN to predict wave height on the basis of actual measurements of wave height, and demonstrated superior results to the use of a single-layered ANN. Tsai and Tsai [16] used ANN to convert pressure signals into the following parameters: the significant wave height, the wave period, the maximum wave height, and the peak of wave spectrum. Other relevant studies include Aminzadeh-Gohari et al. [17], Arena and Puca [18], Chang and Chien [19], Chang and Chien [20], Deo and Naidu [21], Lin-Ye et al. [22], Londhe [23], Ni and Ma [24], Salcedo-Sanz et al. [25], Stefanakos [26], Tseng et al. [27], and Tsai et al. [28]. Numerous studies have employed other artificial intelligence algorithms, such as support vector regression (SVR), which was used by Salcedo-Sanz et al. [25], and the adaptive neuro-fuzzy inference system (ANFIS), notably applied by Karimi et al. [29]. Other studies have compared the use of multiple artificial intelligence models for wave prediction analysis; for example, Malekmohamadi et al. [30] compared SVR, the multilayer perceptron (MLP) neural network, Bayesian networks, and ANFIS models, and Wei [31] compared k-nearest neighbors, linear regressions, model trees, MLP, and SVR models. The aforementioned studies demonstrated that ANN models generate rapid and accurate predictions; therefore, the present study also employed an ANN to establish a wave height prediction model.

2. Data Source

The northeastern sea area of Taiwan was selected as the experimental location of this study (Figure 1) and the buoys of Longdong and Guishandao were chosen as the experimental subjects for wave height prediction. This study compiled data from 2005 to 2015. During some typhoons in this period, the buoys malfunctioned, which resulted in incomplete data records. These typhoon incidents thus had to be disregarded by this study, but complete data existed for 53 typhoons that affected the target area, and they were used in this study.

Table 1. Typhoon incidents between 2005 and 2015.

Year	Typhoon and Date	Year	Typhoon and Date
2005	Matsa (8/3–6), Sanvu (8/11–13), Damrey (9/21–23), Longwang (9/30–10/3)	2011	Aere (5/9–10), Songda (5/27–28), Meari (6/23–25), Muifa (8/4–6), Nanmadol (8/27–30)
2006	Chanchu (5/16–18), Ewiniar (7/7–9), Bilis (7/12–15), Kaemi (7/23–26), Saomai (8/9–10), Bopha (8/7–9), Shanshan (9/14–16)	2012	Talim (6/19–21), Doksuri (6/28–29), Saola (7/30–8/3), Haikui (8/6–7), Kai-Tak (8/14–15), Tembin (8/21–28), Jelawat (9/27–28)
2007	Pabuk (8/6–8), Wutip (8/8–9), Sepat (8/16–19), Mitag (11/26–27)	2013	Soulik (7/11–13), Trami (8/20–22), Kong-Rey (8/27–29), Usagi (9/19–22), Fitow (10/4–7)
2008	Kalmaegi (7/16–18), Fung-Wong (7/26–29), Nuri (8/19–21), Sinlaku (9/11–16), Hagupit (9/21–23), Jangmi (9/26–29)	2014	Hagibis (6/14–15), Matmo (7/21–23), Fung-Wong (9/19–22)
2009	Linfa (6/19–22), Molave (7/16–18), Morakot (8/5–10), Parma (10/3–6)	2015	Noul (5/10–11), Linfa (7/6–9), Chan-Hom (7/9–11)
2010	Lionrock (8/31–9/2), Namtheun (8/30–31), Meranti (9/9–10), Fanapi (9/17–20), Megi (10/21–23)

lists these typhoons and their dates.

This study collected data concerning relevant attributes of the experimental area that might affect wave height. First, sea and land typhoon warnings issued by the CWB were compiled. The warnings contained data concerning the following four attributes of each typhoon: the atmospheric pressure at the typhoon center, the maximum wind speed at the typhoon center, the latitude of the typhoon center, and the longitude of the typhoon center. Data collected from observation stations included meteorological data and oceanographic data. Meteorological data were obtained by the land-based weather stations affiliated with the CWB located in Keelung, Pengjiayu, Suao, and Yilan. Data from the weather stations comprised the following four attributes: ground air pressure, average wind speed, maximum 10-min mean wind speed, and maximum instantaneous wind speed. Oceanographic data, including significant wave height, were obtained by the CWB Longdong and Guishandao buoys. All the wave heights mentioned in this study refer to the significant wave heights. The aforementioned data were organized and processed with interpolation and supplementing, which yielded 3052 entries of data recorded at hourly intervals.

Table 2. Statistical attributes of the typhoons, meteorological data, and buoy-obtained data.

Attribute (unit)	Min–Max, Mean	Attribute (unit)	Min–Max, Mean
Pressure at the typhoon center (hPa)	910.0–998.0, 965.7	Maximum instantaneous wind speed at Pengjiayu (m/s)	2.0–65.8, 19.2
Iintensity of the typhoon (km/h)	54.0–198.0, 121.9	Ground air pressure at Suao (hPa)	966.7–1011.9, 998.3
Latitude of the typhoon center (degree)	15.9–29.1, 22.4	Average wind speed at Suao (m/s)	0–33.4, 4.7
Longitude of the typhoon center (degree)	113.9–130.9, 122.1	Maximum 10-min mean wind speed at Suao (m/s)	0.3–37.2, 6.3
Ground air pressure at Keelung (hPa)	934.6–1011.2, 997.2	Maximum instantaneous wind speed at Suao (m/s)	1.7–62.4, 12.1
Average wind speed at Keelung (m/s)	0–24.0, 5.0	Ground air pressure at Yilan (hPa)	968.6–1013.6, 1000.4
Maximum 10-min mean wind speed at Keelung (m/s)	0–25.1, 6.3	Average wind speed at Yilan (m/s)	0.1–25.2, 3.8
Maximum instantaneous wind speed at Keelung (m/s)	0.1–39.6, 11.7	Maximum 10-min mean wind speed at Yilan (m/s)	0.1–29.6, 5.0
Ground air pressure at Pengjiayu (hPa)	955.0–1003.8, 990.3	Maximum instantaneous wind speed at Yilan (m/s)	0.1–48.5, 8.8
Average wind speed at Pengjiayu (m/s)	0–44.3, 11.3	Wave height at Longdong (m)	0.2–11.2, 2.2
Maximum 10-min mean wind speed at Pengjiayu (m/s)	0.9–48.4, 12.7	Wave height at Guishandao (m)	0.2–16.4, 2.3

presents the attributes, their unit, and the statistical values (including maximal, minimal, and mean values) of the 53 typhoons.

3. Model Development

3.1. Artificial Neural Network (ANN)

This study employed a well-developed ANN model to establish a wave height prediction model. The theoretical basis of the ANN model is as follows. An ANN simulates the neural transmissions of human brains and performs parallel distributed computations using multiple nonlinear arithmetic units, or neurons, and their connections. Through a large amount of numerical data, a computer performs constant learning and convergence and adjusts weight value between units to train the ANN to generate the results and answers sought by researchers.

McCulloch and Pitts [32] first proposed using a model—the ANN—based on mathematical and logical algorithms that functions similarly to the neural transmissions of a brain. After considerable research and failures, the development of computer science led to the proposal of the back propagation network (BPN) by Rumelhart and McClelland [33]. The BPN became the most frequently used neural network because it enabled model optimization and resolved numerous problems encountered by earlier research. The BPN is a supervised learning method with a feedforward framework and multilayered perception. The multiple layers are generally categorized as the input layer, hidden layer, and output layer. The computation equation in the hidden layer is as follows:

$$o_h=f({\displaystyle {\sum }_i{w}_{hi}}{o}_i+{\theta }_h)$$

(1)

where $o_h$ refers to the output signal of the hth processing unit (neuron) in the hidden layer, and $f$ represents the activation function of the processing units. The term $w_{hi}$ refers to the weight between the hth unit in the hidden layer and ith unit in the input layer, $o_i$ represents the output value of ith unit in the input layer, and ${\theta }_h$ represents the threshold of the hth unit in the hidden layer.

The equation in the output layer is as follows:

$$o_k=f({\displaystyle {\sum }_k{w}_{kh}}{o}_h+{\theta }_k)$$

(2)

where $o_k$ refers to the output signal of the kth processing unit in the output layer, $w_{kh}$ refers to the weight between the kth unit in the output layer and hth unit in the hidden layer, and ${\theta }_k$ represents the threshold of the kth unit in the output layer.

The BPN learning algorithm is divided into forward propagation and backward propagation. Forward propagation means the input enters through the input layer and undergoes weight processing in the hidden layer and then yields an output value after going through a conversion function. If the output value is critically different from the target output value, the steepest descent method is applied to solve for the correction value of the weight; this value is then used for backward propagation. Forward and backward propagations are continually performed until the error between the output value and target output value meets a certain standard. This generates the optimal weight and achieves BPN convergence. The equation for the error function E is as follows:

$$E=\frac{1}{2}{{\displaystyle \sum }}_k\left(d_k-o_k\right)2$$

(3)

where $d_k$ represents the target value of the kth unit in the output layer.

The partial differential equation for the error function and weight is as follows:

$$\Delta w=-\eta \frac{\partial E}{\partial w}$$

(4)

where $\Delta w$ represents the weight correction value between the processing units of each layer, and $\eta$ represents the learning rate that controls the value of each weight correction. The weight correction $\Delta w_{kh}$ between the hth unit in the hidden layer and the kth unit in the output layer is as follows:

$$\Delta w_{kh}=\eta \times {\delta }_k\times o_h$$

(5)

where ${\delta }_k=\left(d_k-o_k\right)o_k\left(1-o_k\right)$.

The weight correction $\Delta w_{hi}$ between the ith unit in the input layer and the hth unit in the hidden layer is as follows:

$$\Delta w_{hi}=\eta \times {\delta }_h\times o_i$$

(6)

where ${\delta }_h=o_h\left(1-o_h\right){{\displaystyle \sum }}_k\left({\delta }_k{w}_{\mathit{kh}}\right)$.

3.2. Data Partitioning

Numerous empirical methods are used for optimizing an ANN model. As indicated in Pasini [34], a training-validation-test procedure is usually adopted for the optimization of an ANN model. This study employed the procedure. To establish the model, the typhoons selected for use in this study were divided into training, validation, and testing sets. The 30 typhoons that occurred between 2005–2010 in the training set were used to establish the model structure and adjust the model parameters for the ANN output to approach the target value. The BPN algorithm is applied on a training set, then, at each step of iteration, the performance of the obtained input-output map is validated on the validation set (12 typhoons occurred at years 2011 and 2012). This procedure, called early stopping, is performed to avoid the overfitting due to a too much close reconstruction of the data in the training set. The typhoons (11 typhoons occurred between 2013–2015) in the testing set, completely unknown to the network, were used to verify the selected models.

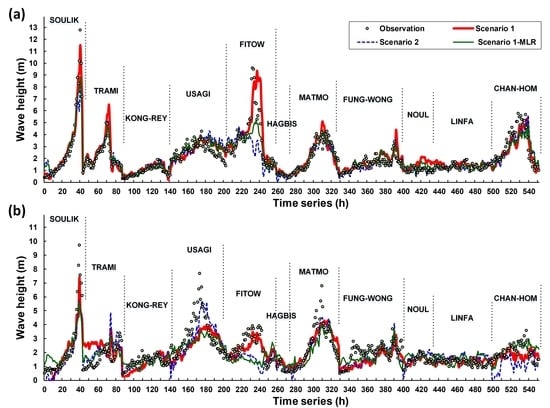
Wave Heights in the Testing Set

The typhoons in the testing set were Soulik, Trami, Kong-Rey, Usagi, Fitow, Hagibis, Matmo, Fung-Wong, Noul, Linfa, and Chan-Hom. The paths of these 11 typhoons are presented in Figure 2. This section discusses the wave height changes recorded at Longdong and Guishandao (i.e., the observation values) in light of the various paths of the typhoons, which are discussed further with respect to prediction outcomes and the performance of the prediction model.

Figure 3 presents the observation record of the significant wave height of all the typhoons in the testing set. The observed wave heights recorded by the Longdong and Guishandao buoys are both present to facilitate the comparison of wave height changes during the same typhoon. According to Figure 3, the wave height varied considerably during typhoons Soulik, Usagi, Fitow, and Matmo. Figure 4 presents the maximum wave height (shorten as MWH) and mean value of the wave height (AWH) of typhoons in the testing set to compare the wave heights of said typhoons. Here, the AWH is computed by averaging the measurements from the individual typhoon. The following observations can be made according to Figure 4: (1) The MWH recorded at Longdong was 12.79 m during typhoon Soulik and the maximal AWH was 3.71 m during typhoon Fitow, and at Guishandao, the MWH of 9.72 m was also recorded during typhoon Soulik, but the maximal AWH of 3.27 m was recorded during typhoon Usagi. (2) The highest MWH values were both recorded during typhoon Soulik, and the recorded wave height at Longdong was 3.07 m higher than that at Guishandao.

Among the typhoons for which the recorded wave height at Longdong was higher than that at Guishandao, typhoon Soulik is discussed first in this section. Typhoon Soulik was classified as a typhoon of intense intensity—an intensity level at which the wind intensity is greater than 51.0 m/s, as defined by the CWB—and the records indicate that the lowest pressure recorded at its center was 925 hPa, the maximum wind speed close to its center was 51 m/s, and the maximum instantaneous wind speed was 72 m/s. The path of Soulik was a generally westward path from east to west (Figure 2a), and the typhoon made landfall on Taiwan after passing through the Longdong and Guishandao buoys. Consequently, it had a considerable effect on both buoys and caused severe wind waves that resulted in wave height records that were notably higher than during the other typhoons. Typhoon Fitow was classified as a typhoon of moderate intensity—an intensity level at which the wind intensity ranges from 32.7 to 50.9 m/s, as defined by the CWB—and the records indicated its lowest pressure at center was 960 hPa, its maximum wind speed close to the center was 38 m/s, and its maximum instantaneous wind speed was 54 m/s. Although typhoon Fitow caused a remarkable wave height at Longdong, the recorded wave height at Guishandao was only 3.92 m. The difference between the records of the two buoys was as much as 5.68 m. As depicted in Figure 2e, the path of typhoon Fitow went from east to west and passed through the border of the research area without making landfall on Taiwan. Nevertheless, this typhoon caused remarkable wave heights at the Longdong buoy. However, the Guishandao buoy recorded less remarkable wave heights, which might have resulted from the fact that when the periphery of the typhoon touched the landmass of Taiwan, its structure was damaged and it became less powerful. Other typhoons with similar paths such as typhoons Trami (Figure 2b) and Chan-Hom (Figure 2k) also resulted in similar wave records.

Conversely, several typhoons generated considerably higher records of maximum and average wave heights at Guishandao than at Longdong. These situations can be categorized into three types: (1) typhoons that passed through the east coast of Taiwan moving from south to north, including Kong-Rey, Fung-Wong, and Noul; (2) a typhoon that passed through the Central Mountain Range, namely typhoon Matmo; and (3) a typhoon that passed by the south of Taiwan through the Bashi Channel, namely typhoon Usagi. In these situations, the Guishandao buoy was directly affected by the typhoon, whereas the height of wind waves recorded at Longdong decreased under the protection of the Central Mountain Range that disrupted the peripheral structure of the typhoon.

3.3. Case Modeling and Parameter Calibration

The input attributes for the model proposed in this study included the typhoon warnings and data collected by weather stations and buoys as presented in Section 2. The pressure at the typhoon center, maximum wind speed at the typhoon center, latitude of the typhoon center, and longitude of the typhoon center were the four attributes collected from the warnings and were represented in sequence from A₁ to A₄; the attributes obtained by the land-based weather stations were represented in sequence from B_1,j to B_4,j, which refer to the ground air pressure, average wind speed, maximum 10-min mean wind speed, and maximum instantaneous wind speed, respectively; moreover, when j = 1, 2, 3, and 4, the numbers refer to Keelung, Pengjiayu, Suao, and Yilan, respectively. The wave heights observed at the buoys were represented by H₁ and H₂, which refer to Longdong and Guishandao, respectively.

3.3.1. Cases of the Length of Lag Times

This study designed five variations of lag time to test and select the optimal prediction. Lag times varying from the current moment (Δt = 0) to 4 h ahead (Δt = 4) were tested and marked as Case 1 to Case 5. This study tested the wave height prediction of the next hour to determine the length of the lag time Δt. In other words, Case 1 used all the attribute data of the current moment (Δt = 0), Case 2 applied the attribute data of the current moment (Δt = 0) and that of 1 h ahead (Δt = 1), and so on for Case 3 and the rest. Therefore, the prediction equation for the Longdong buoy is as follows:

H_1,t+1 = f{(A_i,t−k)_{i=1,4;k=0,∆t}, (B_i,j,t−k)_{i=1,4; j=1,4;k=0,∆t}, (H_i,t−k)_i=2;k=0,∆t}

(7)

where t represents the time index. Particularly, with respect to the prediction of wave height for the Longdong buoy, only the wave height attributes from Guishandao, rather than those from the Longdong buoy, were applied. This measure was used to ensure that even if the Longdong buoy malfunctioned, the data collected from the Guishandao buoy could still be used for Longdong buoy predictions.

The prediction equation for the Guishandao buoy is as follows:

H_2,t+1 = f{(A_i,t−k)_{i=1,4;k=0,∆t}, (B_i,j,t−k)_{i=1,4; j=1,4;k=0,∆t}, (H_i,t−k)_i=1;k=0,∆t}

(8)

Likewise, for the prediction of wave height at the Guishandao buoy, only attribute data from the Longdong buoy were applied for the same reason mentioned in the previous paragraph.

3.3.2. Definition of the Evaluation Indexes

This study used the following indexes to determine the performance of the prediction model: mean absolute error (MAE), root mean square error (RMSE), relative MAE (rMAE), relative RMSE (rRMSE), correlation coefficient (CC), and CE. The calculations of each index are as follows:

$$\mathrm{MAE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|H_{i,pre}-H_{i,obs}\right|$$

(9)

$$\mathrm{rMAE}=\frac{\mathrm{M}\mathrm{A}\mathrm{E}}{{\overline{H}}_{i,obs}}$$

(10)

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(H_{i,pre}-H_{i,obs}\right)}^2}{n}}$$

(11)

$$\mathrm{rRMSE}=\frac{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}{{\overline{H}}_{i,obs}}$$

(12)

$$\mathrm{CC}=\frac{{{\displaystyle \sum }}_{i=1}^n\left(H_{i.pre}-{\overline{H}}_{i,pre}\right)\left(H_{i.obs}-{\overline{H}}_{i,obs}\right)}{{{\displaystyle \sum }}_{i=1}^n{\left(H_{i,pre}-{\overline{H}}_{i,pre}\right)}^2{{\displaystyle \sum }}_{i=1}^n{\left(H_{i,obs}-{\overline{H}}_{i,obs}\right)}^2}$$

(13)

$$\mathrm{CE}=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(h_{i.obs}-h_{i,pre}\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(h_{i,obs}-{\overline{h}}_{i,obs}\right)}^2}$$

(14)

where n represents the number of data entries, $H_{i,pre}$ represents the predicted wave height at buoy i, and $H_{i,obs}$ represents the observed wave height at buoy i. Moreover, ${\overline{H}}_{i,pre}$ represents the predicted average wave height at buoy i and ${\overline{H}}_{i,obs}$ represents the observed average wave height at buoy i.

3.3.3. Modeling and Parameter Calibration

This study established an ANN-based prediction model using nntool toolbox in Matlab. The training set was used to establish the model structure and train the model parameters. With respect to the BPN framework design, the number of hidden layers was one and the number of neurons in the hidden layer was set to be solved from the following equation: (number of neurons in the input layer + number of neurons in the output layer − 1)/2, according to Trenn [35]. In addition, the activation function between the input layer and hidden layer was the log-sigmoid transfer function and the activation function between the hidden layer and output layer was a linear transfer function. The Levenberg-Marquardt training algorithm was used for the training function and the learning rate was set at default.

Momentum is a variable that affects the weight of forward input. The introduction of the momentum term is used to accelerate the learning process by triggering the weight changes to continue in the same direction with larger steps. Furthermore, the momentum term prevents the learning process from settling in a local minimum. Because the momentum parameter ranged between 0 and 1, this study conducted a test on this parameter and set the interval at 0.1. This parameter was then substituted into the five cases described in Section 3.3.1 and the RMSE between the prediction outcome and observed wave height was calculated. Figure 5 presents the analyses for both the Longdong and Guishandao buoys using the validation set. With respect to the Longdong buoy, when the momentum was 1.0, 0.6, 0.4, 0.4, and 0.8 for Cases 1 to 5, minimal RMSE values of 1.597 m, 1.552 m, 1.562 m, 1.564 m, and 1.578 m were obtained, respectively. For the Guishandao buoy, Cases 1 to 5 obtained minimal RMSE values of 1.023 m, 1.011 m, 1.053 m, 1.080 m, and 1.115 m for momenta of 0.8, 0.4, 0.5, 0.8, and 0.5, respectively. According to these outcomes, applying Case 2 with a momentum of 0.6 would attain the optimal solution for the Longdong buoy, whereas applying Case 2 with a momentum of 0.4 would attain the optimal solution for the Guishandao buoy.

4. Analysis of Scenarios and Evaluations

4.1. Designed Scenarios—Whether to Use Data from the Adjacent Buoy

This section discusses Scenarios 1 and 2, which were used to determine whether using data collected by the adjacent buoy for modeling would affect the prediction outcomes. Scenario 1 model input combined all three data sets, namely typhoon warnings, data from weather stations, and data from the adjacent buoy. Scenario 2 excluded the data from the adjacent buoy and used only the data sets concerning typhoon warnings and data from weather stations. Scenario 2 can be understood to represent the hypothetical situation in which the wave height data from both the Longdong and Guishandao buoys were missing and the prediction could only be completed with data from weather stations.

On the basis of the analytic results detailed in the previous section, the Case 2 setting was applied for the model input. The attributes at the current moment (Δt = 0) and at a lag time of 1 h (Δt = 1) were used for input. The Case 2 setting was used for model input in the rest of this study. The prediction models for both Scenarios 1 and 2 with the lead time of 1 h at the Longdong buoy are represented as follows:

Scenario 1: H_1,t+1 = f{(A_i,t−k)_i=1,4;k=0,1, (B_i,j,t−k)_{i=1,4; j=1,4;k=0,1}, (H_i,t−k)_i=2;k=0,1}

(15)

Scenario 2: H_1,t+1 = f{(A_i,t−k)_i=1,4;k=0,1, (B_i,j,t−k)_{i=1,4; j=1,4;k=0,1}}

(16)

For the buoy at Guishandao, the prediction models for both Scenarios 1 and 2 with the lead time of 1 h are represented as follows:

Scenario 1: H_2,t+1 = f{(A_i,t−k)_i=1,4;k=0,1, (B_i,j,t−k)_{i=1,4; j=1,4;k=0,1}, (H_i,t−k)_i=1;k=0,1}

(17)

Scenario 2: H_2,t+1 = f{(A_i,t−k)_i=1,4;k=0,1, (B_i,j,t−k)_{i=1,4; j=1,4;k=0,1}}

(18)

4.2. Prediction Outcomes

Figure 6 presents the prediction outcomes of both buoys for all the typhoons in the testing set with a lead time of 1 h; the black-edged circles represent the observed data, solid red lines represent Scenario 1, and blue dotted lines represent Scenario 2. The figure indicates that the results of Scenario 1 were closer to the observed data than those of Scenario 2. Scenario 2 notably underestimated wave height for various typhoons; for example, data for typhoons Soulik and Fitow at Longdong and typhoons Soulik, Fitow, and Matmo at Guishandao. Scenario 1 achieved a satisfactory level of performance for Longdong, but underestimated the wave height for typhoons Usagi and Matmo at Guishandao. Figure 7a,c depicts the distribution of observation values and prediction values, and the results indicate the following: (1) the CE of Scenario 1 had stronger agreement than that of Scenario 2 at both Longdong and Guishandao, which means that Scenario 1 had better fitting results; however, the CE of Scenario 1 at Guishandao was only slightly higher than that of Scenario 2; (2) in Scenario 1, the gradients were 0.8996 and 0.5829 for the Longdong and Guishandao buoys, respectively, which means that the prediction outcomes for Longdong presented less underestimation for wave height than Guishandao.

To compare the accuracy achieved using ANNs of Scenario 1, a traditional multiple linear regression (MLR) model (namely, Scenario 1-MLR) was applied as a benchmark. In Figure 6, the prediction results obtained using the ANN-based Scenario 1 are satisfactorily consistent with the observed data compared to Scenario 1-MLR. Moreover, the results in Figure 7b,d show that the slopes calculated are greater in the case of Scenario 1 than in the case of Scenario 1-MLR, indicating that the estimates obtained using the ANN models were closer to the observed results than the estimates obtained using the MLR models.

Figure 8 presents the calculation results of the prediction error using several evaluation indexes. The absolute errors (i.e., MAE an RMSE) of Scenario 1 were generally less than those of Scenario 1-MLR and Scenario 2 for both buoys, indicating that Scenario 1 had overall superior performance with respect to errors. With respect to relative errors (i.e., rMAE and rRMSE) and CE, Scenario 1 also outperformed Scenario 1-MLR and Scenario 2. Moreover, the CE of Scenario 1 was higher for the Longdong buoy (CE = 0.802) than for the Guishandao buoy (CE = 0.565).

4.3. Evaluation and Discussion

4.3.1. Evaluation: According to Wave Classification

In the previous section, the results indicated that Scenarios 1 and 2 performed differently when wave height was high (Figure 7); therefore, this study proceeded to calculate the predictive error for various wave classifications. The wave classification system of the CWB served as the reference for this study. Waves were classified into the following three types: waves with a height less than 1.5 m were small waves, those with a height between 1.5 m and 2.5 m were moderate waves, and those with a height higher than 2.5 m were high waves.

Figure 9 presents the values of the absolute error (RMSE) and relative error (rRMSE) when the waves were classified as small, moderate, or high. According to Figure 9a,c, the results of the absolute error (RMSE) for both Longdong and Guishandao exhibited the estimated pattern—the error was relatively low for small waves and relatively high for high waves. The results from comparing the outcomes of each wave classification are as follows:

• Small waves resulted in similar outcomes in Scenarios 1 and 2 at the Longdong buoy, yielding results of 0.378 m and 0.380 m, respectively. However, at the Guishandao buoy, the value of absolute error for Scenario 1 was 0.653 m, which was higher than that for the Scenario 2 value of 0.509 m. Thus, Scenario 1 was not advantageous for predicting small waves.
• Results from both buoys for both moderate and high waves demonstrated that Scenario 1 had a lower value of absolute error than Scenario 2. Particularly, the results for high waves at Longdong yielded a major difference of 0.445 m (RMSE with Scenario 1 = 1.101 m; RMSE with Scenario 2 = 1.546 m).

With respect to rRMSE, the results for the Longdong buoy (Figure 9b) indicated that (1) the rRMSE of Scenario 1 decreased progressively among the small, moderate, and high wave classifications, suggesting that Scenario 1 mitigated the relative error better as the waves grew higher; and (2) the values of rRMSE in Scenario 2 for all three classifications of waves were between 0.36 and 0.38. The results for the Guishandao buoy (Figure 9d) indicated that the relative errors for small waves in Scenarios 1 and 2 were both high (0.610 and 0.476, respectively), whereas the relative errors for both moderate and high waves were lower than 0.4.

4.3.2. Evaluation: According to Each Typhoon

This section evaluates the error values for each typhoon in the testing set. Figure 10 presents the RMSE of each typhoon in the testing set for the Longdong buoy and Guishandao buoy. This figure also presents the prediction results of Scenarios 1 and 2. The results demonstrated that the typhoons with relatively high error values, indicated by an RMSE higher than 1, were typhoons Soulik (Scenario 2) and Fitow (Scenarios 1 and 2) at the Longdong buoy and typhoons Soulik (Scenarios 1 and 2), Trami (Scenario 1), Usagi (Scenarios 1 and 2), Fitow (Scenario 2), and Chan-Hom (Scenario 2) at the Guishandao buoy. Five typhoons had a high RMSE at Guishandao compared with two at Longdong, which suggested that wave height prediction at Guishandao might be more complex. This study determined several possible factors that may have added to the difficulty of wave prediction at Guishandao, resulting in a higher prediction error at Guishandao—the path of the typhoons, the location of the buoy, the geographical environment, and typhoon intensity.

This study determined that Scenario 1 did not always outperform Scenario 2 for all the typhoons in the testing set; thus, adding data from buoys did not guarantee prediction accuracy. Scenario 2 did perform better, as is evident from the relatively low RMSEs, for typhoons Trami, Matmo, Fung-Wong, and Noul at Longdong and Trami, Kong-Rey, Usagi, Hagibis, and Matmo at Guishandao. Differences between Scenarios 1 and 2 attributable to the differences between typhoon paths are discussed in the following section.

4.3.3. Evaluation: According to Typhoon Path

This study classified the paths of the 11 typhoons in the testing set into four general types. Path-1 refers to the path by which typhoons pass through the north end of Taiwan via the northeastern sea area. Typhoons that took this path were Soulik, Trami, Fitow, and Chan-Hom. Path-2 refers to the path by which typhoons go from south to north along the east coast of Taiwan; Kong-Rey, Fung-Wong, and Noul took this path. Path-3 refers to the path that crosses the main island of Taiwan through the Central Mountain Range; typhoon Matmo took this path. Path-4 refers to the path by which typhoons pass through the south end of Taiwan via the Bashi Channel or other situations such as when typhoons develop in the South China Sea; such typhoons included Usagi, Hagibis, and Linfa.

Figure 11 presents the RMSE and rRMSE results for the various types of typhoon paths. The results from the Longdong buoy indicated that Longdong was superior when Path-1 or Path-4 was taken under the Scenario 1 setting, or when Path-2 or Path-3 was taken under the Scenario 2 setting. The following conclusions were made on the basis of the results from Longdong buoy: (1) a Path-1 classification meant that the typhoon passed by the research area going east to west; therefore, information from the adjacent buoy could largely mitigate the prediction error (the difference of RMSE between the two scenarios reached 0.43 m); (2) because the storm area of typhoons with a Path-4 trajectory was not part of the research area, the oscillation of waves detected at the northeastern coast were long waves generated by the energy transmitted from afar; therefore, information from the adjacent buoy enabled accurate prediction; and (3) the storm areas of typhoons with Path-2 and Path-3 trajectories were strongly disrupted by topography—the Central Mountain Range, resulting in irregular disturbances of offshore wind waves; thus, the adjacent buoy could not provide effective information for wave height predictions. The prediction results at Guishandao were similar, but the information from the adjacent buoy did not improve predictions, according to the long wave prediction results for Path-4.

4.3.4. Evaluation: Prediction with Lead Time Varying from 1 to 6 H

Wave height predictions for a lead time of 1 to 6 h were evaluated. The Scenario 1 model was applied to conduct the comparison for both the prediction simulation and evaluation of indexes. The equations used were as follows:

H_1,t+L = f{(A_i,t−k)_i=1,4;k=0,1, (B_i,j,t−k)_{i=1,4; j=1,4;k=0,1}, (H_i,t−k)_i=2;k=0,1}

(19)

H_2,t+L = f{(A_i,t−k)_i=1,4;k=0,1, (B_i,j,t−k)_{i=1,4; j=1,4;k=0,1}, (H_i,t−k)_i=1;k=0,1}

(20)

Figure 12 and Figure 13 present the wave height prediction results for the Longdong and Guishandao buoys with a lead time varying from 2 to 6 h. The results of a lead time of 1 h is presented in Figure 6. As the lead time lengthened, the prediction accuracy worsened. Figure 14 presents the calculation results of each evaluation index when lead time varied from 1 to 6 h; the results were used to determine the diffusion of prediction error. Figure 14a–d indicates that the errors at Longdong were lower than those at Guishandao when the lead time varied from 1 to 5 h, whereas at a lead time of 6 h, the error at Longdong surpassed that at Guishandao. However, at a lead time of 6 h, the absolute and relative errors for both buoys were considerably large, which diminished the reliability of prediction values. Generally, a reasonable threshold for the error item is set up to determine lead time length for wave height forecast in practice. For example, when the acceptable threshold for wave height prediction was set at rMAE = 0.3, the lead time for Longdong buoy was 4 h, whereas for Guishandao it was 2 h, as depicted in Figure 14b. Finally, both the CC (Figure 14e) and CE (Figure 14f) were higher at Longdong than at Guishandao at a lead time of from 1 to 6 h.

5. Conclusions

Taiwan is located in the area through which typhoons frequently pass. Because it is unprotected by the Central Mountain Range, the east of Taiwan often receives a direct impact. The area is affected by typhoons earlier than the rest of the region and usually faces the brunt of remarkably powerful winds, rains, and wind waves. The periphery of a typhoon may cause long waves even before the arrival of its center. Long waves with longer waves may transmit the waves to a particularly faraway location. Moreover, when such waves reach the shore, topography may cause the wave to swell into exceptionally high waves referred to as rogue waves. Rogue waves generally occur when typhoons occur at an outer sea area, and the public often neglects the danger of seaside activities during the time before the typhoon arrives.

The CWB of Taiwan has set up the Longdong and Guishandao buoys in the northeastern sea area to conduct long-term monitoring of relevant oceanographic data. However, the loss of records or other malfunctions have caused a lack of comprehensive information concerning wind waves. The present study thus hypothesized that if wave heights around a particular buoy could be predicted using data from the adjacent buoy when the target buoy malfunctioned, the problems associated with buoy malfunctioning could be overcome and key information regarding the waves in the target area could still be collected.

The aim of this study was to evaluate the feasibility of predicting waves using the data collected by the adjacent buoy. This study applied an ANN to establish a wave height prediction model. After the model was established, two scenarios were tested to assess performance. Scenario 1 included information from the adjacent buoy and Scenario 2 did not.

The present study successfully determined the feasibility of using information from the adjacent buoy to predict waves. Key findings concerning the overall error of predictions are as follows:

• Scenario 1 achieved superior performance to Scenario 2 with respect to absolute errors (MAE and RMSE), relative errors (rMAE and rRMSE), and CE. Moreover, the CE of Longdong (0.802) was higher than that of Guish andao (0.565); moreover, the results concerning Longdong in Scenario 1 exhibited less underestimation of high wave heights than those for Guishandao.
• When the waves were classified as small, moderate, or high, the evaluation based on rRMSE yielded the following results. The values of rRMSE for each wave classification for Longdong in Scenario 1 progressively decreased in the order of small, moderate, and high waves; this phenomenon demonstrated that the Scenario 1 setting had the ability to reduce relative error when the wave height increased. The other finding demonstrated that the values of the relative error for small waves at Guishandao in Scenarios 1 and 2 were relatively higher at 0.610 and 0.476, respectively.
• An examination of each typhoon indicated that they took various types of paths; for example, typhoons passed the northeastern sea area from east to west, passed from south to north along the east coast, passed through the Central Mountain Range, or passed by the south end of Taiwan through the Bashi Channel. Various types of typhoon paths caused the periphery of the typhoon to become disrupted by the topography or the Central Mountain Range, which increased the complexity of making wind wave predictions and caused prediction accuracy to vary between the Longdong and Guishandao buoys.