Characterization of Diffuse Groundwater Inflows into Stream Water (Part II: Quantifying Groundwater Inflows by Coupling FO-DTS and Vertical Flow Velocities)
Abstract
:1. Introduction
2. Materials and Methods
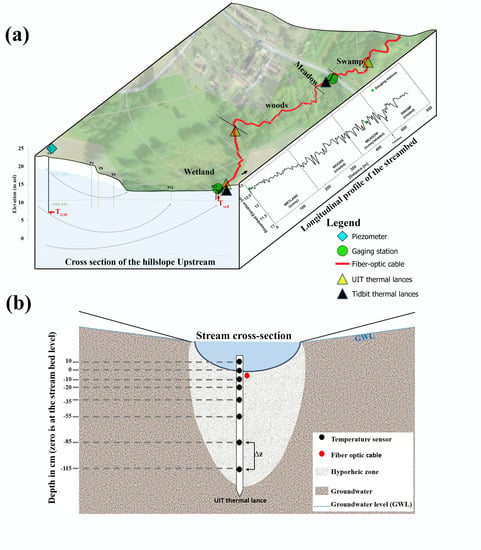
2.1. Hydraulics of the Study Site
2.2. Temperature Measurements: DTS Set-up and Thermal Profiles
2.3. Framework for Quantifying Hyporheic Exchanges: Calculating Vertical Flows
2.4. Framework for Quantifying Hyporheic Exchanges: Coupling FO-DTS and Punctual Data
2.5. Framework for Quantifying Hyporheic Exchanges: Comparing Vertical Velocities to Volumetric Discharge
3. Results and Discussion
3.1. Groundwater Inflow Mapping
3.2. Evolution of Thermal Profiles in the Hyporheic Zone
3.3. Vertical Flow Velocities at Locations without Groundwater Inflows
3.4. Vertical Flow Velocities in Groundwater–influenced Locations
3.5. Comparison of Groundwater Discharge Estimation Methods
3.6. Limits of Our Method and Perspectives
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Freeze, R.A. Role of subsurface flow in generating surface runoff: 1. Base flow contributions to channel flow. Water Resour. Res. 1972, 8, 609–623. [Google Scholar] [CrossRef]
- Hester, E.T.; Gooseff, M.N. Moving Beyond the Banks: Hyporheic Restoration Is Fundamental to Restoring Ecological Services and Functions of Streams. Environ. Sci. Technol. 2010, 44, 1521–1525. [Google Scholar] [CrossRef]
- Hester, E.T.; Brooks, K.E.; Scott, D.T. Comparing reach scale hyporheic exchange and denitrification induced by instream restoration structures and natural streambed morphology. Ecol. Eng. 2018, 115, 105–121. [Google Scholar] [CrossRef]
- Alexander, M.D.; Caissie, D. Variability and comparison of hyporheic water temperatures and seepage fluxes in a small Atlantic salmon stream. Groundwater 2003, 41, 72–82. [Google Scholar] [CrossRef]
- Barlow, J.R.; Coupe, R.H. Groundwater and surface-water exchange and resulting nitrate dynamics in the Bogue Phalia basin in northwestern Mississippi. J. Environ. Qual. 2012, 41, 155–169. [Google Scholar] [CrossRef]
- Baxter, C.V.; Hauer, F.R. Geomorphology, hyporheic exchange, and selection of spawning habitat by bull trout (Salvelinus confluentus). Can. J. Fish. Aquat. Sci. 2000, 57, 1470–1481. [Google Scholar] [CrossRef]
- Hillyard, R.W.; Keeley, E.R. Temperature-Related Changes in Habitat Quality and Use by Bonneville Cutthroat Trout in Regulated and Unregulated River Segments. Trans. Am. Fish. Soc. 2012, 141, 1649–1663. [Google Scholar] [CrossRef]
- Vidon, P.; Allan, C.; Burns, D.; Duval, T.P.; Gurwick, N.; Inamdar, S.; Lowrance, R.; Okay, J.; Scott, D.; Sebestyen, S. Hot Spots and Hot Moments in Riparian Zones: Potential for Improved Water Quality Management1. J. Am. Water Resour. Assoc. 2010, 46, 278–298. [Google Scholar] [CrossRef]
- Harvey, J.; Gooseff, M. River corridor science: Hydrologic exchange and ecological consequences from bedforms to basins. Water Resour. Res. 2015, 51, 6893–6922. [Google Scholar] [CrossRef]
- Lee, D.R.; Hynes, H. Identification of groundwater discharge zones in a reach of Hillman Creek in southern Ontario. Water Qual. Res. J. 1978, 13, 121–134. [Google Scholar] [CrossRef]
- Libelo, E.L.; MacIntyre, W.G. Effects of surface-water movement on seepage-meter measurements of flow through the sediment-water interface. Appl. Hydrogeol. 1994, 2, 49–54. [Google Scholar] [CrossRef]
- McCallum, J.L.; Cook, P.G.; Berhane, D.; Rumpf, C.; McMahon, G.A. Quantifying groundwater flows to streams using differential flow gaugings and water chemistry. J. Hydrol. 2012, 416, 118–132. [Google Scholar] [CrossRef]
- Ruehl, C.; Fisher, A.; Hatch, C.; Los Huertos, M.; Stemler, G.; Shennan, C. Differential gauging and tracer tests resolve seepage fluxes in a strongly-losing stream. J. Hydrol. 2006, 330, 235–248. [Google Scholar] [CrossRef]
- Frei, S.; Gilfedder, B. FINIFLUX: An implicit finite element model for quantification of groundwater fluxes and hyporheic exchange in streams and rivers using radon. Water Resour. Res. 2015, 51, 6776–6786. [Google Scholar] [CrossRef]
- Pittroff, M.; Frei, S.; Gilfedder, B. Quantifying nitrate and oxygen reduction rates in the hyporheic zone using 222Rn to upscale biogeochemical turnover in rivers. Water Resour. Res. 2017, 53, 563–579. [Google Scholar] [CrossRef]
- Westhoff, M.C.; Savenije, H.H.G.; Luxemburg, W.M.J.; Stelling, G.S.; van de Giesen, N.C.; Selker, J.S.; Pfister, L.; Uhlenbrook, S. A distributed stream temperature model using high resolution temperature observations. Hydrol. Earth Syst. Sci. 2007, 11, 1469–1480. [Google Scholar] [CrossRef]
- Briggs, M.A.; Lautz, L.K.; McKenzie, J.M. A comparison of fibre-optic distributed temperature sensing to traditional methods of evaluating groundwater inflow to streams. Hydrol. Process. 2012, 26, 1277–1290. [Google Scholar] [CrossRef]
- Gonzalez-Pinzon, R.; Ward, A.S.; Hatch, C.E.; Wlostowski, A.N.; Singha, K.; Gooseff, M.N.; Haggerty, R.; Harvey, J.W.; Cirpka, O.A.; Brock, J.T. A field comparison of multiple techniques to quantify groundwater–surface-water interactions. Freshw. Sci. 2015, 34, 139–160. [Google Scholar] [CrossRef]
- Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring methods for groundwater surface water interactions: A review. Hydrol. Earth Syst. Sci. 2006, 10, 873–887. [Google Scholar] [CrossRef]
- Poulsen, J.R.; Sebok, E.; Duque, C.; Tetzlaff, D.; Engesgaard, P.K. Detecting groundwater discharge dynamics from point-to-catchment scale in a lowland stream: Combining hydraulic and tracer methods. Hydrol. Earth Syst. Sci. 2015, 19, 1871–1886. [Google Scholar] [CrossRef]
- Anderson, M.P. Heat as a ground water tracer. Groundwater 2005, 43, 951–968. [Google Scholar] [CrossRef]
- Constantz, J. Interaction between stream temperature, streamflow, and groundwater exchanges in Alpine streams. Water Resour. Res. 1998, 34, 1609–1615. [Google Scholar] [CrossRef]
- Tristram, D.A.; Krause, S.; Levy, A.; Robinson, Z.P.; Waller, R.I.; Weatherill, J.J. Identifying spatial and temporal dynamics of proglacial groundwater–surface-water exchange using combined temperature-tracing methods. Freshw. Sci. 2015, 34, 99–110. [Google Scholar] [CrossRef]
- Stallman, W.R. Steady One-Dimensional Fluid Flow in a Semi-Infinite Porous Medium with Sinusoidal Surface Temperature. J. Geophys. Res. 1965, 70, 2821–2827. [Google Scholar] [CrossRef]
- Hatch, C.E.; Fisher, A.T.; Revenaugh, J.S.; Constantz, J.; Ruehl, C. Quantifying surface water–groundwater interactions using time series analysis of streambed thermal records: Method development. Water Resour. Res. 2006, 42, 14. [Google Scholar] [CrossRef]
- Briggs, M.A.; Lautz, L.K.; McKenzie, J.M.; Gordon, R.P.; Hare, D.K. Using high-resolution distributed temperature sensing to quantify spatial and temporal variability in vertical hyporheic flux. Water Resour. Res. 2012, 48, 1–16. [Google Scholar] [CrossRef]
- Briggs, M.A.; Lautz, L.K.; Buckley, S.F.; Lane, J.W. Practical limitations on the use of diurnal temperature signals to quantify groundwater upwelling. J. Hydrol. 2014, 519, 1739–1751. [Google Scholar] [CrossRef]
- Käser, D.H.; Binley, A.; Heathwaite, A.L.; Krause, S. Spatio-temporal variations of hyporheic flow in a riffle-step-pool sequence. Hydrol. Process. Int. J. 2009, 23, 2138–2149. [Google Scholar] [CrossRef]
- Krause, S.; Blume, T.; Cassidy, N. Investigating patterns and controls of groundwater up-welling in a lowland river by combining Fibre-optic Distributed Temperature Sensing with observations of vertical hydraulic gradients. Hydrol. Earth Syst. Sci. 2012, 16, 1775–1792. [Google Scholar] [CrossRef]
- Hurtig, E.; Grosswig, S.; Kuhn, K. Distributed fibre optic temperature sensing: A new tool for long-term and short-term temperature monitoring in boreholes. Energy Sources 1997, 19, 55–62. [Google Scholar] [CrossRef]
- Hausner, M.B.; Suarez, F.; Glander, K.E.; van de Giesen, N.; Selker, J.S.; Tyler, S.W. Calibrating Single-Ended Fiber-Optic Raman Spectra Distributed Temperature Sensing Data. Sensors 2011, 11, 10859–10879. [Google Scholar] [CrossRef]
- Tyler, S.W.; Selker, J.S.; Hausner, M.B.; Hatch, C.E.; Torgersen, T.; Thodal, C.E.; Schladow, S.G. Environmental temperature sensing using Raman spectra DTS fiber-optic methods. Water Resour. Res. 2009, 45, 11. [Google Scholar] [CrossRef] [Green Version]
- Van de Giesen, N.; Steele-Dunne, S.C.; Jansen, J.; Hoes, O.; Hausner, M.B.; Tyler, S.; Selker, J. Double-Ended Calibration of Fiber-Optic Raman Spectra Distributed Temperature Sensing Data. Sensors 2012, 12, 5471–5485. [Google Scholar] [CrossRef] [Green Version]
- Moffett, K.B.; Tyler, S.W.; Torgersen, T.; Menon, M.; Selker, J.S.; Gorelick, S.M. Processes controlling the thermal regime of saltmarsh channel beds. Environ. Sci. Technol. 2008, 42, 671–676. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; Briggs, M.A.; Delin, G.; Hare, D.K. Combined use of thermal methods and seepage meters to efficiently locate, quantify, and monitor focused groundwater discharge to a sand-bed stream. Water Resour. Res. 2016, 52, 4486–4503. [Google Scholar] [CrossRef] [Green Version]
- Selker, J.S.; Thevenaz, L.; Huwald, H.; Mallet, A.; Luxemburg, W.; de Giesen, N.V.; Stejskal, M.; Zeman, J.; Westhoff, M.; Parlange, M.B. Distributed fiber-optic temperature sensing for hydrologic systems. Water Resour. Res. 2006, 42, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Selker, J.S.; van de Giesen, N.; Westhoff, M.; Luxemburg, W.; Parlange, M.B. Fiber optics opens window on stream dynamics. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Westhoff, M.C.; Gooseff, M.N.; Bogaard, T.A.; Savenije, H.H.G. Quantifying hyporheic exchange at high spatial resolution using natural temperature variations along a first-order stream. Water Resour. Res. 2011, 47, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Lauer, F.; Frede, H.G.; Breuer, L. Uncertainty assessment of quantifying spatially concentrated groundwater discharge to small streams by distributed temperature sensing. Water Resour. Res. 2013, 49, 400–407. [Google Scholar] [CrossRef]
- Le Lay, H.; Thomas, Z.; Rouault, F.; Pichelin, P.; Moatar, F. Characterization of diffuse groundwater inflows into stream water. Part I: Spatial and temporal mapping framework based on fiber optic distributed temperature sensing. Water 2019, 11, 2389. [Google Scholar] [CrossRef] [Green Version]
- Lowry, C.S.; Walker, J.F.; Hunt, R.J.; Anderson, M.P. Identifying spatial variability of groundwater discharge in a wetland stream using a distributed temperature sensor. Water Resour. Res. 2007, 43, 1–9. [Google Scholar] [CrossRef]
- Mamer, E.A.; Lowry, C.S. Locating and quantifying spatially distributed groundwater/surface water interactions using temperature signals with paired fiber-optic cables. Water Resour. Res. 2013, 49, 7670–7680. [Google Scholar] [CrossRef]
- Sebok, E.; Duque, C.; Engesgaard, P.; Boegh, E. Application of Distributed Temperature Sensing for coupled mapping of sedimentation processes and spatio-temporal variability of groundwater discharge in soft-bedded streams. Hydrol. Process. 2015, 29, 3408–3422. [Google Scholar] [CrossRef]
- Unland, N.P.; Cartwright, I.; Andersen, M.S.; Rau, G.C.; Reed, J.; Gilfedder, B.S.; Atkinson, A.P.; Hofmann, H. Investigating the spatio-temporal variability in groundwater and surface water interactions: A multi-technique approach. Hydrol. Earth Syst. Sci. 2013, 17, 3437–3453. [Google Scholar] [CrossRef] [Green Version]
- Tirado-Conde, J.; Engesgaard, P.; Karan, S.; Müller, S.; Duque, C. Evaluation of Temperature Profiling and Seepage Meter Methods for Quantifying Submarine Groundwater Discharge to Coastal Lagoons: Impacts of Saltwater Intrusion and the Associated Thermal Regime. Water 2019, 11, 1648. [Google Scholar] [CrossRef] [Green Version]
- Varli, D.; Yilmaz, K. A Multi-Scale Approach for Improved Characterization of Surface Water—Groundwater Interactions: Integrating Thermal Remote Sensing and in-Stream Measurements. Water 2018, 10, 854. [Google Scholar] [CrossRef] [Green Version]
- Carlson, A.K.; Taylor, W.W.; Schlee, K.M.; Zorn, T.G.; Infante, D.M. Projected impacts of climate change on stream salmonids with implications for resilience-based management. Ecol. Freshw. Fish 2017, 26, 190–204. [Google Scholar] [CrossRef]
- Hendriks, D.M.D.; Kuijper, M.J.M.; van Ek, R. Groundwater impact on environmental flow needs of streams in sandy catchments in the Netherlands. Hydrol. Sci. J. 2014, 59, 562–577. [Google Scholar] [CrossRef] [Green Version]
- Laize, C.L.R.; Meredith, C.B.; Dunbar, M.J.; Hannah, D.M. Climate and basin drivers of seasonal river water temperature dynamics. Hydrol. Earth Syst. Sci. 2017, 21, 3231–3247. [Google Scholar] [CrossRef] [Green Version]
- Hongve, D. A revised procedure for discharge measurement by means of the salt dilution method. Hydrol. Process. 1987, 1, 267–270. [Google Scholar] [CrossRef]
- Calkins, D.; Dunne, T. A salt tracing method for measuring channel velocities in small mountain streams. J. Hydrol. 1970, 11, 379–392. [Google Scholar] [CrossRef]
- Sloto, R.A.; Crouse, M.Y. HYSEP: A Computer Program for Streamflow Hydrograph Separation and Analysis. In Water–Resources Investigations Report; USGS Numbered Series; U.S. Geological Survey: Reston, VA, USA, 1996; p. 46. [Google Scholar] [CrossRef]
- Freeze, R.A. Streamflow generation. Rev. Geophys. 1974, 12, 627–647. [Google Scholar] [CrossRef]
- Boulton, A.J.; Findlay, S.; Marmonier, P.; Stanley, E.H.; Valett, H.M. The functional significance of the hyporheic zone in streams and rivers. Annu. Rev. Ecol. Syst. 1998, 29, 59–81. [Google Scholar] [CrossRef] [Green Version]
- Cardenas, M.B. Hyporheic zone hydrologic science: A historical account of its emergence and a prospectus. Water Resour. Res. 2015, 51, 3601–3616. [Google Scholar] [CrossRef]
- Thomas, Z.; Rousseau-Gueutin, P.; Kolbe, T.; Abbott, B.W.; Marçais, J.; Peiffer, S.; Frei, S.; Bishop, K.; Pichelin, P.; Pinay, G.; et al. Constitution of a catchment virtual observatory for sharing flow and transport models outputs. J. Hydrol. 2016, 543, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Gordon, R.P.; Lautz, L.K.; Briggs, M.A.; McKenzie, J.M. Automated calculation of vertical pore-water flux from field temperature time series using the VFLUX method and computer program. J. Hydrol. 2012, 420, 142–158. [Google Scholar] [CrossRef]
- Benyahya, L.; Caissie, D.; Satish, M.G.; El-Jabi, N. Long-wave radiation and heat flux estimates within a small tributary in Catamaran Brook (New Brunswick, Canada). Hydrol. Process. 2012, 26, 475–484. [Google Scholar] [CrossRef]
- Caissie, D. The thermal regime of rivers: A review. Freshw. Biol. 2006, 51, 1389–1406. [Google Scholar] [CrossRef]
- Petrides, A.C.; Huff, J.; Arik, A.; van de Giesen, N.; Kennedy, A.M.; Thomas, C.K.; Selker, J.S. Shade estimation over streams using distributed temperature sensing. Water Resour. Res. 2011, 47, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Irvine, D.J.; Cranswick, R.H.; Simmons, C.T.; Shanafield, M.A.; Lautz, L.K. The effect of streambed heterogeneity on groundwater–surface water exchange fluxes inferred from temperature time series. Water Resour. Res. 2015, 51, 198–212. [Google Scholar] [CrossRef]
- Vandersteen, G.; Schneidewind, U.; Anibas, C.; Schmidt, C.; Seuntjens, P.; Batelaan, O. Determining groundwater–surface water exchange from temperature-time series: Combining a local polynomial method with a maximum likelihood estimator. Water Resour. Res. 2015, 51, 922–939. [Google Scholar] [CrossRef]
- Abrol, I.; Palta, J. Bulk density determination of soil clods using rubber solution as a coating material. Soil Sci. 1968, 106, 465–468. [Google Scholar] [CrossRef]
- Lapham, W.W. Use of temperature profiles beneath streams to determine rates of vertical ground-water flow and vertical hydraulic conductivity. In Water Supply Paper; U.S. Geological Survey: Reston, VA, USA, 1989. [Google Scholar] [CrossRef]
- Stonestrom, D.A.; Constantz, J. Using Temperature to Study Stream-Ground Water Exchanges; U.S. Geological Survey Fact Sheet: Menlo Park, CA, USA, 2004; pp. 1–4.
- Broecker, T.; Teuber, K.; Sobhi Gollo, V.; Nützmann, G.; Lewandowski, J.; Hinkelmann, R. Integral Flow Modelling Approach for Surface Water–Groundwater Interactions along a Rippled Streambed. Water 2019, 11, 1517. [Google Scholar] [CrossRef] [Green Version]
- Gooseff, M.N.; Anderson, J.K.; Wondzell, S.M.; LaNier, J.; Haggerty, R. A modelling study of hyporheic exchange pattern and the sequence, size, and spacing of stream bedforms in mountain stream networks, Oregon, USA. Hydrol. Process. 2005, 19, 2915–2929. [Google Scholar] [CrossRef]
- Yao, C.; Lu, C.; Qin, W.; Lu, J. Field Experiments of Hyporheic Flow Affected by a Clay Lens. Water 2019, 11, 1613. [Google Scholar] [CrossRef] [Green Version]
- Poblador, S.; Thomas, Z.; Rousseau-Gueutin, P.; Sabaté, S.; Sabater, F. Riparian forest transpiration under the current and projected Mediterranean climate: Effects on soil water and nitrate uptake. Ecohydrology 2019, 12, e2043. [Google Scholar] [CrossRef]
- Frei, S.; Durejka, S.; Le Lay, H.; Thomas, Z.; Gilfedder, B.S. Hyporheic nitrate removal at the reach scale: Exposure times vs. residence times. Water Resour. Res. 2019. [Google Scholar] [CrossRef] [Green Version]
- Duff, J.H.; Toner, B.; Jackman, A.P.; Avanzino, R.J.; Triska, F.J. Determination of groundwater discharge into a sand and gravel bottom river: A comparison of chloride dilution and seepage meter techniques. Int. Ver. Theor. Angew. Limnol. Verh. 2000, 27, 406–411. [Google Scholar] [CrossRef]
- Briggs, M.A.; Voytek, E.B.; Day-Lewis, F.D.; Rosenberry, D.O.; Lane, J.W. Understanding Water Column and Streambed Thermal Refugia for Endangered Mussels in the Delaware River. Environ. Sci. Technol. 2013, 47, 11423–11431. [Google Scholar] [CrossRef]
- Hare, D.K.; Briggs, M.A.; Rosenberry, D.O.; Boutt, D.F.; Lane, J.W. A comparison of thermal infrared to fiber-optic distributed temperature sensing for evaluation of groundwater discharge to surface water. J. Hydrol. 2015, 530, 153–166. [Google Scholar] [CrossRef] [Green Version]
- Shope, C.L.; Constantz, J.E.; Cooper, C.A.; Reeves, D.M.; Pohll, G.; McKay, W.A. Influence of a large fluvial island, streambed, and stream bank on surface water–groundwater fluxes and water table dynamics. Water Resour. Res. 2012, 48, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Van Balen, R.T.; Kasse, C.; De Moor, J. Impact of groundwater flow on meandering; example from the Geul River, The Netherlands. Earth Surf. Process. Landf. 2008, 33, 2010–2028. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water: A Single Resource; United States Geological Survey Circular; DIANE Publishing Inc.: Darby, PA, USA, 1998; Volume 1139. [Google Scholar] [CrossRef]
- Kolbe, T.; Marcais, J.; Thomas, Z.; Abbott, B.W.; de Dreuzy, J.R.; Rousseau-Gueutin, P.; Aquilina, L.; Labasque, T.; Pinay, G. Coupling 3D groundwater modeling with CFC-based age dating to classify local groundwater circulation in an unconfined crystalline aquifer. J. Hydrol. 2016, 543, 31–46. [Google Scholar] [CrossRef] [Green Version]
- Kolbe, T.; de Dreuzy, J.-R.; Abbott, B.W.; Aquilina, L.; Babey, T.; Green, C.T.; Fleckenstein, J.H.; Labasque, T.; Laverman, A.M.; Marçais, J.; et al. Stratification of reactivity determines nitrate removal in groundwater. Proc. Natl. Acad. Sci. USA 2019, 116, 2494–2499. [Google Scholar] [CrossRef] [Green Version]










| Parameter | Symbol (Unit) | Sub-reach | |||
|---|---|---|---|---|---|
| Wetland | Woods | Meadow | Swamp | ||
| Fundamental period to filter | P (day) | 1 | 1 | 1 | 1 |
| Sediment porosity | ɲe (-) | 0.43 (0.01) | 0.40 (0.01) | 0.26 (0.07) | 0.40 (0.01) |
| Sediment thermal dispersivity | b (m) | 0.001 | 0.001 | 0.001 | 0.001 |
| Sediment thermal conductivity | λ0 (cal s−1 cm−1 °C−1) | 0.0045 (0.0001) | 0.0048 (0.0001) | 0.0069 (0.0001) | 0.0048 (0.0001) |
| Sediment volumetric heat capacity | C (cal m−3 °C−1) | 0.643 (0.001) | 0.630 (0.001) | 0.560 (0.002) | 0.630 (0.001) |
| Water volumetric heat capacity | Cw (cal m−3 °C−1) | 1.00 | 1.00 | 1.00 | 1.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Lay, H.; Thomas, Z.; Rouault, F.; Pichelin, P.; Moatar, F. Characterization of Diffuse Groundwater Inflows into Stream Water (Part II: Quantifying Groundwater Inflows by Coupling FO-DTS and Vertical Flow Velocities). Water 2019, 11, 2430. https://doi.org/10.3390/w11122430
Le Lay H, Thomas Z, Rouault F, Pichelin P, Moatar F. Characterization of Diffuse Groundwater Inflows into Stream Water (Part II: Quantifying Groundwater Inflows by Coupling FO-DTS and Vertical Flow Velocities). Water. 2019; 11(12):2430. https://doi.org/10.3390/w11122430
Chicago/Turabian StyleLe Lay, Hugo, Zahra Thomas, François Rouault, Pascal Pichelin, and Florentina Moatar. 2019. "Characterization of Diffuse Groundwater Inflows into Stream Water (Part II: Quantifying Groundwater Inflows by Coupling FO-DTS and Vertical Flow Velocities)" Water 11, no. 12: 2430. https://doi.org/10.3390/w11122430
APA StyleLe Lay, H., Thomas, Z., Rouault, F., Pichelin, P., & Moatar, F. (2019). Characterization of Diffuse Groundwater Inflows into Stream Water (Part II: Quantifying Groundwater Inflows by Coupling FO-DTS and Vertical Flow Velocities). Water, 11(12), 2430. https://doi.org/10.3390/w11122430