Predicting Rainfall and Runoff Through Satellite Soil Moisture Data and SWAT Modelling for a Poorly Gauged Basin in Iran

Abstract

Hydrological models are widely used for many purposes in water sector projects, including streamflow prediction and flood risk assessment. Among the input data used in such hydrological models, the spatial-temporal variability of rainfall datasets has a significant role on the final discharge estimation. Therefore, accurate measurements of rainfall are vital. On the other hand, ground-based measurement networks, mainly in developing countries, are either nonexistent or too sparse to capture rainfall accurately. In addition to in-situ rainfall datasets, satellite-derived rainfall products are currently available globally with high spatial and temporal resolution. An innovative approach called SM2RAIN that estimates rainfall from soil moisture data has been applied successfully to various regions. In this study, first, soil moisture content derived from the Advanced Microwave Scanning Radiometer for the Earth observing system (AMSR-E) is used as input into the SM2RAIN algorithm to estimate daily rainfall (SM2R-AMSRE) at different sites in the Karkheh river basin (KRB), southwest Iran. Second, the SWAT (Soil and Water Assessment Tool) hydrological model was applied to simulate runoff using both ground-based observed rainfall and SM2R-AMSRE rainfall as input. The results reveal that the SM2R-AMSRE rainfall data are, in most cases, in good agreement with ground-based rainfall, with correlations R ranging between 0.58 and 0.88, though there is some underestimation of the observed rainfall due to soil moisture saturation not accounted for in the SM2RAIN equation. The subsequent SWAT-simulated monthly runoff from SM2R-AMSRE rainfall data (SWAT-SM2R-AMSRE) reproduces the observations at the six gauging stations (with coefficient of determination, R² > 0.71 and NSE > 0.56), though with slightly worse performances in terms of bias (Bias) and root-mean-square error (RMSE) and, again, some systematic flow underestimation compared to the SWAT model with ground-based rainfall input. Additionally, rainfall estimates of two satellite products of the Tropical Rainfall Measuring Mission (TRMM), 3B42 and 3B42RT, are used in the calibrated SWAT- model after bias correction. The monthly runoff predictions obtained with 3B42- rainfall have 0.42 < R² < 0.72 and−0.06 < NSE < 0.74 which are slightly better than those obtained with 3B42RT- rainfall, but not as good as the SWAT-SM2R-AMSRE. Therefore, despite the aforementioned limitations, using SM2R-AMSRE rainfall data in a hydrological model like SWAT appears to be a viable approach in basins with limited ground-based rainfall data.

1. Introduction

Reliable prediction of runoff in large catchments has been a subject of interest in hydrologic sciences for some time and is significant for sustainable management of water resources, design of water infrastructure, and flood risk management [1,2,3]. Understanding the complex relationships between rainfall and runoff processes is essential to accurately predicting surface runoff [4]. This can be achieved by hydrological modeling which, besides simulating surface runoff, also aids in understanding, predicting, and managing water resources and modeling impacts of climate and land use changes on the surface water balance [5].

The Semi-distributed Soil Water Assessment Tool (SWAT) hydrological model [6] is one of the most useful tools for simulating runoff, sediment and water quality of agricultural watersheds over the last decades [7]. The SWAT model, which requires numerous input parameters, e.g. soil, land-use, topography, meteorological data, should be calibrated and validated at monitoring stations to reduce the error between measured and predicted outputs, before applying the model for specific analyses or predictions [8,9]. However, the performance of hydrological models in predicting streamflow relies heavily on the quality and spatial distribution of the input rainfall observations [10,11,12]. Although rain gauges as reference instruments provide accurate measurements of rainfall, because of the variability of rainfall in time and space, they do not often provide adequate spatial representation of rainfall, especially in poorly gauged basins [13].

Using remotely-sensed rainfall products, which are nowadays available at various resolutions (temporal and spatial) and with increased accuracy, is an alternative to the use of rain gauge-observed data. Some recent studies used satellite-derived rainfall in hydrological modeling [14,15,16,17,18,19]. For instance, Stisen and Sandholt [20] evaluated the performance of five satellite-based rainfall products with different spatial resolutions as input into the MIKE SHE model for runoff simulation of four sub-basins of the Senegal River basin in West Africa. They showed a significant improvement in runoff prediction performance when the model is recalibrated using bias-corrected satellite rainfall data with rain gauge observations. Thiemig et al. [21] investigated the suitability of satellite-derived rainfall estimates as forcing data for the LISFLOOD hydrological model, applying two different bias-correction methods to correct the bias in the satellite-based rainfall estimates.

Among the satellite-based rainfall predictions, the TRMM Multi-Satellite Precipitation Analysis (TMPA) products [22] are still the most widely used in various research studies and applications [23,24]. For example, Dinku et al. [25] evaluated the TMPA-3B43 rainfall products with nine other satellite-based rainfall using a rain gauge network over Ethiopia. Their results showed that TMPA-3B43 performs very well with a Bias value less than 10% and a relative root-mean-square error of about 25% at the monthly time scale.

Another approach, overcoming some of the known deficiencies of classical measurements of rainfall, like rain gauge data, is a recently developed method called SM2RAIN proposed by Reference [26], which provides an area-integrated time-accumulated rainfall measurement from soil moisture (SM) data based on the inversion of the soil water balance equation. Brocca et al. [27] carried out a thorough analysis of the physical consistency of the SM2RAIN algorithm, its hypothesis, and performance, using in-situ SM observations as input. For this purpose, different formulations of the SM2RAIN algorithm were applied to 10 sites across Europe. The results showed that SM2RAIN performed very well in the synthetic experiments with a correlation coefficient between synthetically generated and simulated data, at daily time step, higher than 0.940 and an average bias lower than 4%. However, generally, the temporal and spatial scale of ground SM measurements, especially in developing countries, is limited and insufficient. Hence, satellite SM observations, which use images retrieved from either passive or active microwave sensors, can be used due to their ease of operation, global coverage, and good accuracy [28].

However, the derivation of accurate and reliable SM from satellite remote sensing still represents a challenging task because of uncertainty of inexact instrument calibration, errors in the retrieval algorithms, noise in the microwave signal, and data transmission failure [29,30].

Nowadays, satellite SM products are available at different spatial and temporal resolution (e.g. References [31,32]). Two space-borne satellite missions, such as Soil Moisture and Ocean Salinity (SMOS) mission launched by the European Space Agency (ESA) in 2009 [33] and Soil Moisture Active Passive (SMAP) launched by the National Aeronautics and Space Administration (NASA) in 2015 [34], were placed in orbit and dedicated specifically to measure SM. Advanced Microwave Scanning Radiometer—Earth Observing System (AMSR-E) on board of the NASA’s AQUA satellite is one of the most commonly used sensor for SM retrieval over the last years, as it has been available from years 2002–2011 (e.g. References [35,36]). However, because of the rather shallow remotely sensed depth of the bare soil layer for AMSR-E SM (<1 cm), attenuation of the electromagnetic signal is further increased by dense vegetation, snow-covered, and frozen soils [37].

SM estimation based on both active and passive microwave sensors was evaluated in several studies (e.g. References [38,39,40]). For instance, Rahmani et al. [28] extracted surface SM from SMOS and the active + passive ESA Climate Change Initiative SM products to investigate the correlation between surface SM products and monthly precipitation and temperature data observations in six different regions of Iran, with the final purpose of drought monitoring. The results reveled that the agreement between all surface SM products was quite satisfactory with correlation coefficients higher than 0.5. Babaian et al. [41] evaluated the accuracy of different simulated surface soil moisture data (using observed van Genuchten-Mualem hydraulic parameters and those obtained with parametric transfer functions) along with retrieved soil moisture content (using ENVISAT/ASAR active microwave and the inversion algorithm of IEM estimates) in the Zanjanrood River sub-basin of northwestern Iran. The findings indicated the feasibility of using spectral data to predict VGM hydraulic parameters and soil water dynamics at the larger scales. Al-Yaari et al. [42] evaluated two passive (SMOS) and active (ASCAT) satellite microwave products at the global scale with respect to SM simulations from MERRA-Land. They found that ASCAT SM product is prone to larger random errors in Iran.

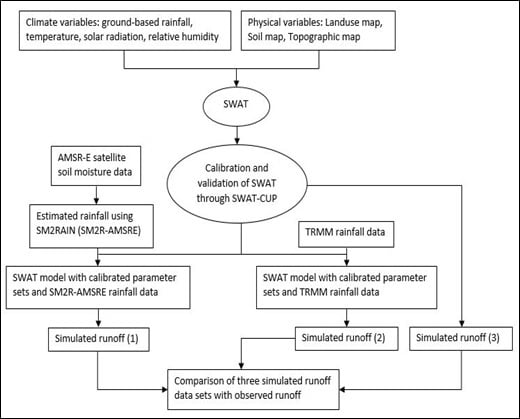
The objective of this work is twofold. First, we aim to evaluate the accuracy of rainfall estimates obtained from SM2RAIN. For this purpose, the AMSR-E SM product generated by implementing the standard NASA algorithm is used as input into the SM2RAIN algorithm to estimate rainfall, called SM2R-AMSRE, at 10 different sites in the Karkheh river basin (KRB). The lack of in-situ SM measurements in Iran, but the availability of AMSR-E SM data over the modeling time period (2003–2006), are the main reasons for choosing the AMSR-E SM product for this study. Moreover, the quality of the SM2RAIN rainfall estimations was evaluated further by comparing them with TRMM-satellite- predicted rainfall for two versions of the seven TRMM-TMPA-products, daily near-real-time (3B42RT) and research-grade (3B42) after bias correction with in-situ rainfall.

Second, we aim to assess the suitability of SM2R-AMSRE as input for the calibrated-SWAT model for monthly streamflow simulation at six gauging stations of the KRB. Similarly, the two bias-corrected versions of TMPA- products were employed in the calibrated-SWAT model as well to predict the monthly surface runoff at the same gauging stations. Model performances were assessed by comparing observed and predicted monthly runoff obtained through ground-based, SM2RAIN-estimated, and satellite-based rainfall inputs.

2. Materials and Methods

2.1. Study Area and Data Collection

The 50,700 km² area KRB (Figure 1), mainly characterized by Mediterranean climate conditions, is located in southwest Iran, between 30°58–34°56 N latitude and 46°06–49°10 E longitude. Due to its large area and its topography ranging from mountains above 3600 m a.s.l. in the northern part to the lowlands in the southern parts, the KRB is characterized by different climate conditions.

Mean annual precipitation ranges from 150 mm in the lower arid plains to 750 mm in the mountainous regions in the northern KRB [43]. The catchment has arid and semi-arid climate and most of the annual water flow (more than 64%) occurs during the months January to May [44].

Geographical characteristics of the flow gauging and climate stations in the KRB are shown in

Table 1. Geographical characteristics of the selected gauging (left) and climate (right) stations.

Streamgauge Station	Longitude (Degrees East)	Latitude (Degrees North)	Elevation (Masl)	Climate Station	Longitude (Degrees East)	Latitude (Degrees North)	Elevation (Masl)
Aran (Ar)	47.92	34.42	1440	Hamedan	48.53	34.87	1741
Polchehr (Pl)	47.43	34.35	1280	Kermanshah	47.15	34.35	1319
Ghurbaghestan(Gh)	47.25	34.23	1230	Eslamabad	46.47	34.12	1349
Hulian (Hu)	47.25	33.75	900	Malayer	48.85	34.25	1778
Afarineh (AF)	47.89	33.33	820	Broujerd	48.75	33.92	1629
Jelogir (Jl)	47.80	32.97	350	Ilam	46.43	33.63	1337
				Khorramabad	48.28	33.43	1148
				Dehloran	47.27	32.68	232
				Dezful	48.38	32.40	143
				Ahvaz	48.67	31.33	22

. The multipurpose Karkheh reservoir, with a designed storage capacity of 7.5 × 10⁹ m³ and net storage capacity of 4.7 × 10⁹ m³, provides water for irrigation of 320,000 ha of agricultural areas in the lower sections of the KRB, as well as generates 934 GWh hydroelectric power per year and controls flood on the river.

Fereidoon and Koch [45] simulated the long-term monthly discharge in the KRB and found that reservoir regulations significantly altered the monthly discharge regime in the lower parts of the Karkheh dam, where, among others, streamflow decreased by 30–50%. Therefore, as the river flow downstream of the dam is strongly controlled by the reservoir operation rules and, as they are unknown, we excluded the two downstream gauging station in this study and considered only the six remaining gauging stations upstream of the Karkheh dam (see Table 1).

The basic input data used in SWAT model consists of a Digital Elevation Model (DEM) map, provided by Shuttle Radar Topography Mission (SRTM) of NASA at a resolution of 90 m, and a soil map obtained from the global map of the Food and Agriculture Organization of the United Nations (FAO, 1995). Moreover, a 900 m-resolution land-use map is provided by Mahab Ghods Consulting Engineers Co. Daily precipitation and maximum and minimum temperature at 10 meteorological stations are obtained from the Iran Meteorological Organization.

In addition, monthly river discharge data from six stream gauges are provided by Iranian Ministry of Energy (Figure 1).

The latest version (7) TMPA-3B42 and TMPA-3B42RT satellite rainfall products (with 0.250 × 0.250 spatial resolution ≈27 km at the Equator) were obtained from (https://pmm.nasa.gov/data-access/downloads/trmm) in daily temporal resolution (accessed on 28 July 2018).

2.2. AMSR-E Soil Moisture Product

The Advanced Microwave Scanning Radiometer (AMSR-E) on-board the NASA’s Aqua satellite was a passive microwave radiometer, observing brightness temperatures at six different frequencies ranging from 6.9–89.0 GHz. It was launched in May 2002 with a spatial sampling resolution of 25 km and ceased operations in December 2011. There are several retrieval algorithms available for determining SM products from the AMSR-E data. The daily surface SM product used in this study is based on the NASA algorithm [37,46] and extracted directly from the gridded Level-3 land surface product (AE_Land3).

2.3. Hydrological Model SWAT and Its Implementation to KRB Basin

The SWAT model is a semi-distributed hydrological model that operates on a daily time-step and was developed to assess the impact of water flow, agricultural management practices, sediment, and nutrient transport simulation in large complex river basins under different hydrologic, geologic, and climatic conditions [6]. SWAT is one of the most widely used hydrological model and has found countless applications all across the world, with a focus on the simulation of regional hydrological impact of climate change [47,48,49]. In the SWAT model, a catchment or basin is divided into a number of sub-basins (=198 in the present basin), which are then, based on the soil type, land-use, and, optionally, slope characteristics, further subdivided into so-called hydrologic response units (HRUs) with identical characteristic of some of these properties. For the large and complex KRB, the total number of HRUs is more than 11,000 (see [45], for details).

For climate input, SWAT uses the data from the weather station closest to the centroid of each subbasin. Calibration, validation, and sensitivity analysis are necessary steps for building SWAT hydrologic model with meaningful range of many “tuning” parameters. This has historically been done by trial and error, but can be carried out an automatic procedure. The SWAT-CUP tool, with the SUFI-2 algorithm, was used in the current study [50] for model calibration and uncertainty analysis of monthly streamflow. In SUFI-2, the performance of the model is evaluated by two indices: P-factor and R-factor. The P-factor is the fraction of measured data covered by the 95 Percent Prediction Uncertainty (95 PPU) band. The propagation of uncertainties in SWAT parameters leads to uncertainties in the model output variables (surface run off in this study), which are expressed as 95% probability distributions. The 95 PPU is calculated at 2.5% and 97.5% levels of the cumulative distribution of an output variable obtained through Latin hypercube sampling [50]. The R-factor is the average width of the 95 PPU band divided by the standard deviation of the measured variable. P-factors range between 0 and 1, with values close to 1 indicating a high model performance, while R-factors range between 0 and infinity, with R above 0.5 to be acceptable for monthly runoff [50]. The quality of the fit of the model output to the observed streamflow data is measured by the root mean square error, RMSE, the determination coefficient, R², and the Nash–Sutcliff efficiency, NSE (e.g. Brocca et al. [50]).

2.4. SM2RAIN Algorithm

The physical processes in the land part of the hydrologic cycle can be described by the soil water balance equation [26]:

$$nZ ds\left(t\right)/dt=p\left(t\right)-q\left(t\right)-e\left(t\right)-g\left(t\right)$$

(1)

where n [-] is the soil porosity, Z [L] is the soil layer depth, $s\left(t\right)$ [-] is the relative soil moisture, t [T] is the time, and p, q, e, and g [L/T] are the precipitation, surface runoff, evapotranspiration, and drainage rate (subsurface flow plus deep percolation), respectively. By solving this equation for p and knowing all other variables the rainfall p for each time step can be retrieved from soil moisture data. Moreover, as shown in Reference [27], the surface runoff q can be assumed to be negligible.

The drainage rate $g\left(t\right)$ is estimated using the following relationship (e.g. [27]).

$$g\left(t\right)=a s\left(t\right){ }^b$$

(2)

where a [L/T] and b [-] are unknown empirical parameters and are going to be calibrated later. $g\left(t\right)$ is the sum of deep percolation and lateral flow.

The (actual) evapotranspiration rate $e\left(t\right)$ is represented by a product of the potential evapotranspiration $E{T}_p\left(t\right)$ and the relative soil water content $s\left(t\right)$ (e.g. Reference [51]):

$$e\left(t\right)=E{T}_p\left(t\right)\times s\left(t\right)$$

(3)

where $E{T}_p\left(t\right)$ is calculated by means of the theoretical Blaney and Criddle approach as modified by Reference [52]:

$$E{T}_p\left(t\right)=-2+c \left[\xi \left(0.46T_a\left(t\right)+8.13\right)\right]$$

(4)

where Ta [C⁰] is the mean air temperature, ξ is the fraction of daytime hours for the time step used (daily in this study) in the total daytime hours of the year, and c is a parameter—to be determined in the calibration process further down—that depends on the daytime wind speed, minimum relative humidity, and actual insolation time. Although a value of c = 1.26 was proposed for this parameter in many studies (see e.g. Reference [27]), it will be further optimized in the calibration process within an acceptable range (0.8–2.1). Therefore, based on Equations (2)–(4), SM2RAIN requires SM and air temperature data for estimating rainfall.

The parameter values nZ, a, b, and c in Equations (2)–(4) are calibrated by matching the SM2RAIN simulated rainfall with the ground observed data using nonlinear least squares, where the RMSE is used as objective function

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left(P_i-O_i\right){ }^2}$$

(5)

where P_i is the SM2RAIN—predicted daily rainfall (SM2R-AMSRE) and O_i is the daily ground-based observed rainfall at station i. The RMSE is minimized by a MATLAB-programed nonlinear constrained optimization method with the named unknown parameters constrained by appropriate bounds.

2.5. SWAT-Modeling Approach Using Weather-Station- and SM2R-AMSRE Precipitation Data

Figure 2 shows the flowchart of the various steps to set up and run the SWAT model with ground-based weather station precipitation, as well as satellite-based SM2RAIN data. After the SM2RAIN algorithm is applied at the locations of weather stations in the KRB to determine the satellite-based rainfall product, SM2R-AMSR, the latter is then used in the calibrated SWAT- model to predict the monthly runoff between the time period January 2000 and September 2006. The results obtained in this way are then compared with the SWAT- model output acquired using the in-situ rain gauge observations as input in the model during the same time period.

3. Results and Discussion

3.1. SWAT-Calibration, Validation, and Sensitivity Analysis of Streamflow Discharge

The application of SWAT model for estimating runoff in other river basins of Iran demonstrates the importance of river discharge monitoring in Iran, which is mostly located in arid and semi-arid regions of the middle east (see e.g. Reference [53]). To evaluate the SWAT model performance for discharge estimation at six gauge stations of the KRB using ground-based precipitation data, the historical time series from 1985–1999 is considered. Calibration and validation were performed on measured stream flows for the 1985–1995 and 1995–1999 time periods, respectively, whereas three years (1982–1984) were considered for model warm up in SWAT before calibration. A set of sensitive model parameters is identified in the calibration procedure (see

Table 2. Initial and final ranges of the seven most sensitive SWAT calibration parameters in the (KRB).

Parameter	Definition	Initial Range	Final Range
r__CN2	SCS runoff curve number	−0.4–0.4	−0.32–(−0.16)
v__GWQMN	Threshold depth of water in shallow aquifer required for return flow	1500–3500	1520–2538
v__ALPHA_BF	Base flow alpha factor	0.4–1	0.56–0.87
v__EPCO	Plant uptake compensation factor	0.2–0.7	0.27–0.55
r__SOL_BD	Moist bulk density	0–0.35	0–0.23
v__RCHRG_DP	Deep aquifer percolation fraction	0.1–0.7	0.25–0.64
v__SHALLST	Initial depth of water in shallow aquifer	2500–4000	2930–3849

) in all sub-basins, but with different ranking of sensitivity (see Reference [45] for details).

For example, soil and groundwater parameters are found to be most sensitive in lowland catchments, while runoff parameters are the most sensitive ones in mountainous or low mountain range landscapes [54]. The reason might be that, because under areas with lower slopes, rainfall infiltration accumulates more, leading to higher groundwater levels and, subsequently, to more baseflow contribution to discharge.

Hence, the groundwater parameters RCHRG_DP, GWQMN, SHALLST, and ALPHA_BF, followed by soil parameter SOL_BD, are identified to be more sensitive in the low-elevation (southern) parts of KRB than in the northern part (with higher elevations) [49]. It should be noted that the Curve Number CN at moisture condition II (CN2) is found to be the most sensitive parameter for the watershed as a whole [45]. The final performance of the calibrated model is evaluated by four statistical measures, P-factor, R-factor, R², NSE at the six gauging stations and the results are shown in

Table 3. Statistical measures for monthly outflows at the eight stations for calibration and validation periods.

Station	P-Factor (Cal/Val)	R-Factor (Cal/Val)	R2 (Cal/Val)	NSE (Cal/Val)
Ar	0.78/0.79	1.12/1.09	0.69/0.66	0.68/0.63
Pl	0.81/0.85	1.16/1.11	0.73/0.70	0.72/0.66
Gh	0.89/0.84	1.38/1.03	0.65/0.73	0.68/0.61
Hu	0.72/0.71	1.05/0.88	0.81/0.72	0.66/0.72
Af	0.94/0.88	1.16/0.89	0.72/0.67	0.73/0.67
Jl	0.78/0.75	1.29/0.82	0.78/0.86	0.78/0.74
Pay-e-Pol 1	0.74/0.70	0.96/0.95	0.73/0.69	0.74/0.68
Hamidiyeh 1	0.72/0.68	1.31/1.08	0.77/0.76	0.71/0.69

¹ Stations located downstream of the Karkheh dam and not used in this.

for the calibration and validation periods.

Figure 3 shows that the SWAT-CUP-simulated monthly streamflow at the six gauging stations compares well with the observed data, particularly, when considering the 95% uncertainty band.

3.2. SM2RAIN- Rainfall Estimation Using AMSR-E Soil Moisture Data

The SM2RAIN method is applied to the locations of the five weather stations in the KRB to estimate the rainfall, called SM2R-AMSRE, from the AMSR-E SM data sets. In order to produce a better prediction of the SM2R-AMSRE rainfall, the SM2RAIN model has to be calibrated first. This is done for the period January 1, 2003 to December 31, 2005, then the model is validated for the remaining nine months from January 1, 2006 to September 30, 2006.

For evaluating the performance of the SM2RAIN method, the correlation coefficient R, the RMSE (Equation (5)), RRMSE (relative RMSE), and Bias (estimated—observed) between observed and SM2R-AMSRE values are used. As shown in

Table 4. Statistical performance measures of the SM2RAIN algorithm at the different climate stations.

Climate Station	R [-]		RMSE [mm]		RRMSE [-]		Bias [%]
	Cal	Val	Cal	Val	Cal	Val	Cal	Val
Ahvaz	0.75	0.66	2.52	2.48	4.04	4.51	−1.05	−1.77
Kermanshah	0.69	0.47	3.07	3.91	2.77	3.66	−3.16	−0.18
Hamedan	0.61	0.54	3.06	2.73	3.05	3.97	−2.57	−0.07
Khorramabad	0.58	0.57	4.19	4.32	3.36	3.16	−4.07	−3.92
Ilam	0.64	0.88	5.58	4.77	3.23	3.65	−6.13	−5.79

, the SM2RAIN method is able to reproduce the rainfall data from AMSR-E soil moisture products with reasonable accuracy.

In the validation period, the R-values for all five sites range between 0.57 for Khorramabad to 0.88 for Ilam. The RMSE shows the lowest values at Ahvaz station in accordance with the better R- values there. On the other hand, this station has the highest RRMSE- values, owing to the fact that its average rainfall has the lowest value compared to other stations. The Bias estimates range from −1.05 to −6.13 for stations Ahavz and Ilam, respectively. The negative values of Bias at all stations indicates a typical underestimation of the SM2R-MSRE rainfall for reasons discussed below.

Figure 4 shows both the daily observed and estimated SM2R-AMSRE rainfall, along with the AMSR-E SM time series, for the five climate stations. Obviously, the highest and lowest performance is obtained for stations Ahvaz and Khorramabad, respectively. In general, one can notice from the figure that the SM2RAIN algorithm underestimates the total rainfall amount at all sites. Indeed, at saturation level the SM value remains constant for any rainfall amount, i.e. the SM measurement cannot provide useful information for rainfall estimation. Based on these considerations and the obtained results, it is expected that soil moisture-based methods will provide an underestimation of the total rainfall [26,27,55], due to the saturation of the soil moisture level.

As further shown in Figure 4, the AMSR-E SM time series at Ilam and Khorramabad stations have higher fluctuations than those at other stations. This could be the reason for the lower performance of the SM2RAIN model at these stations. Moreover, the surface condition may also affect the performance so that the stations located in mountainous areas, like Ilam and Khorramabad, owing to the occurrence of frozen soils and snow cover, have lower performances than those located at low altitudes, e.g. Ahvaz. In general, the stations located in drier areas with lower rainfall amounts, like Ahvaz, show better performance, corroborating the saturation statement above. Similarly, high RRMSE- values and more negative of Bias- values at all stations for both calibration and validation periods can be explained by the underestimated SM2R-AMSRE for heavy rainfall events, owing most likely to the aforementioned problem of soil moisture saturation in the SM2RAIN- model.

The four parameter values (see Equations (1)–(3)) found by nonlinear optimization during the calibration of the SM2RAIN models are shown in

Table 5. Optimized parameter values of the SM2RAIN Equations (1)–(3) at the various climate stations.

Climate Station	Zn [mm]	a [mm/d]	b	c
Ahvaz	32.1	39	2.2	1.90
Kermanshah	34.8	50	2.3	2.00
Hamedan	58.3	56	1.5	1.20
Khorramabad	32.9	46	1.9	1.95
Ilam	44.6	87	2.5	1.90

. Similar to previous studies (e.g. References [26,27]), these parameter values are consistent with their expected physical values.

The spatial distributions (drawn using the nearest neighbor procedure for the rainfall in SWAT) of the rain-gauge-measured- and the SM2R-AMSRE estimated mean annual rainfall over the KRB for the January 2003 to September 2006 time period are shown in the two panels of Figure 5. It can be seen that the SM2RAIN method predicts the ground-based observed rainfall in an agreeable manner, though the latter is slightly underestimated in some regions, for the reasons discussed above.

3.3. Contributions of Different Hydrological Components to the SM2RAIN Water Balance Equation

With the purpose of quantifying the contribution of each component of hydrological balance equation (Equation (1)), i.e. soil moisture change, drainage, and evapotranspiration, to the rainfall estimation, calibrated parameter values of the SM2RAIN algorithm are considered for SM2RAIN-AMSRE rainfall simulation. To study in more details, two months, the wet month January 2003 and the dry month July 2004, for stations Kermanshah and Hamedan, respectively, are selected to assess the contribution of the different components to the SM2R-AMSRE rainfall. The results are shown in the corresponding two plots of Figure 6.

It can be seen from the figure that drainage and evapotranspiration contribute the most and least to the SM2R-AMSRE during rainfall, respectively. At both stations, similar to the results obtained by Reference [27], the evapotranspiration has a small contribution to SM2R-AMSRE through SM2RAIN approach. This contribution is even smaller in dry months when the soil moisture content is very low.

3.4. Calibration and Evaluation of TRMM Satellite Precipitation Products (TMPA) over the KRB

Evaluation of multisatellite precipitation products is widely used in hydrological modelling for streamflow simulations. Vu et al. [56] investigated different satellite rainfall products in runoff simulations using the SWAT model in in the Han River Basin of South Korea. The results showed a satisfactory performance, given that TRMM and CMADS rainfall data simulated the Han River streamflow with acceptable accuracy. A similar study over the Luanhe River Basin in China by Ren et al. [57] concluded that TMPA-3B42 rainfall had the highest performance for estimating monthly runoff, while PERSIANN showed unsatisfactory results. Thus, the study provided information on the performance of different satellite rainfall products in hydrologic modeling for the Han River Basin. In addition, the study contributed to enriching the scientific database on hydrologic applications of different satellite precipitation datasets, especially, for data-scarce regions.

As a third approach of rainfall estimation, the TRMM (TMPA) satellite products, 3B42 and 3B42RT, are evaluated over the KRB by comparing them with the ground-based measurements. To reduce differences between in-situ- and TMPA rainfall estimates in each rain gauge location, bias correction factors (CF) are calculated for three-day sequential moving window scales. To this regard, the suitable temporal scale was identified in the cell of each rain gauge to correct the TMPA rainfall values. For a certain day $d$ and gauge $k$, the multiplicative CF at a specific TRMM pixel with an overlain gauge are expressed as follows:

$$C{F}_K^d=\frac{{{\displaystyle \sum }}_{t=d-3}^{t=d+3}{P}_j\left(k,t\right)}{{{\displaystyle \sum }}_{t=d-3}^{t=d+3}{P}_s\left(k,t\right)}$$

(6)

where $P_j$ and $P_s$ represent daily gauge and TMPA rainfall amounts, respectively, at a given gauge/pixel location $k$ and time instant $t$, for three days before/after considered in the sampling window. The uncorrected TMPA rainfall values were multiplied by the CF to obtain the bias- corrected rainfall estimates.

The results after correction are listed in

Table 6. Statistical performances of the bias- corrected TRMM (TMPA3B42, 3B42RT) at the different stations.

Climate Station	R [-]		RMSE [mm]		RRMSE [-]		Bias [%]
	3B42	3B42RT	3B42	3B42RT	3B42	3B42RT	3B42	3B42RT
Ahvaz	0.37	0.36	4.84	3.51	6.88	5.95	0.13	6.87
Kermanshah	0.56	0.49	4.19	4.10	4.14	3.89	−8.79	−18.89
Hamedan	0.53	0.37	3.31	3.97	3.92	4.17	19.02	24.13
Khorramabad	0.76	0.41	5.63	6.07	4.88	4.27	8.80	9.77
Ilam	0.55	0.34	4.27	6.84	3.86	4.34	−4.87	18.84

in terms of the four statistical scores, R, RMSE, RRMSE and Bias. As shown in Table 6, the 3B42 rainfall products provide better performance with regard to R and Bias, while RMSE and RRMSE are slightly lower for 3B42RT than for 3B42.

Moreover, the comparison of the four statistical measures between observed and TMPA products in Table 6 with those of SM2R-AMSR in Table 4, indicates that SM2RAIN predicts the observed rainfall consistently more accurately than TMPA, except for the Bias at Ahvaz station, which is only 0.13% for TMPA-3B42. Habib et al. [58] also made a one-week moving window to decrease the sampling variability of CMORPH data for the hydrological applications in the upper Gigel Abbay catchment, Ethiopia.

3.5. SWAT- Predicted Runoff Driven by Ground-Based-, SM2R-AMSRE- and TMPA- Rainfall

Finally, the January 2003 to September 2006 simulated monthly runoff obtained by using (1) ground-based, (2) the SM2R-AMSRE satellite-based rainfall and the two TRIMM-TMPA products after bias correctio, (3) 3B42, and (4) B42RT as input in the calibrated- SWAT model are compared to each other (Figure 7,

Table 7. Performance measures for SWAT-predicted runoff with ground-based and SM2R-AMSRE rainfall.

Climate Station	SM2R-AMSRE Rainfall					Ground-based Rainfall
	R2	RMSE	RRMSE	NSE	Bias	R2	RMSE	RRMSE	NSE	Bias
Ar	0.72	3.08	2.22	0.60	−0.86	0.83	2.17	3.18	0.79	−1.26
Pl	0.82	18.5	14.8	0.70	−5.31	0.85	10.1	13.8	0.81	−10.2
Gh	0.71	15.5	10.1	0.57	−2.65	0.81	7.72	5.27	0.81	−8.29
Hu	0.87	33.6	27.3	0.76	−13.9	0.89	18.7	19.6	0.84	−19.8
Af	0.82	19.2	14.5	0.56	−10.3	0.88	12.2	11.8	0.75	−13.8
Jl	0.83	50.1	58.6	0.74	−13.8	0.87	38.6	45.1	0.92	−46.3

and

Table 8. Performance measures for SWAT-predicted runoff with the two TRMM-TMPA- predicted rainfalls.

Climate Station	TMPA- 3B42 Satellite Rainfall					TMPA- 3B42RT Satellite Rainfall
	R2	RMSE	RRMSE	NSE	Bias	R2	RMSE	RRMSE	NSE	Bias
Ar	0.53	2.78	1.02	0.46	−0.78	0.23	4.32	1.87	0.19	0.44
Pl	0.67	33.15	1.48	0.39	−1.31	0.35	15.29	1.28	0.21	−0.20
Gh	0.42	65.41	5.14	0.17	−2.31	0.32	27.68	4.15	0.09	0.65
Hu	0.55	39.16	1.73	0.08	−0.92	0.41	19.84	0.76	0.34	−0.60
Af	0.69	59.42	1.15	−0.06	−0.83	0.46	25.81	1.01	−0.20	1.28
Jl	0.72	57.28	0.96	0.74	−63.8	0.51	66.58	0.54	0.52	16.3

). For cases (1) and (2), good SWAT- performances, as indicated by the statistical measures in Table 7, are obtained. Thus, the R²-values for all sites are greater than 0.89 and 0.72, when using ground-based- and SM2R-AMSRE rainfall as SWAT- input, respectively.

The best results in terms of R² and NSE are obtained for Hulian gauge station. As expected, due to the previously noted systematic underestimation of the SM2R-AMSRE rainfall (see Figure 4), the SWAT model using ground-based observed rainfall shows slightly better performance than that using SM2R-AMSRE data. This underestimation is particularly noticeable at the stream peak flows shown in Figure 7.

The statistics of the SWAT-runoff results obtained with the two corrected TRMM-products, 3B42 and 3B42RT, are listed in Table 8 and may be compared with those acquired when using ground-based and SM2R-AMSRE rainfall in Table 7. Thus, one notices that since SM2R-AMSRE was already shown to be more precise than either one of the two TMPA- products, it is of no surprise that the SWAT- runoff simulated using the former as input is also better than those of the latter. Regarding the two TMPA- SWAT- variants, that with 3B42 satellite rainfall shows overall better results in terms of R², but with higher Bias and RMSE than the one using 3B42RT rainfall. The results indicate that the physically based model SM2RAIN [30], at least in this study, superior to TRMM satellite precipitation both in terms of rainfall and runoff estimation accuracy.

4. Conclusions

The estimation of river discharge in poorly gauged basin is fundamental for flood risk mitigation and water resources management. Among the different hydrological variables that have an impact on water discharge, rainfall is considered the most important. The recently developed SM2RAIN algorithm [51] can be used for rainfall estimation from satellite soil moisture observations and it has been successfully applied to many regions (e.g. Reference [59]). However, the use of SM2RAIN-derived rainfall for river discharge estimation is less explored [18,60,61].

In this study, the SM2RAIN algorithm is successfully applied in the semi-arid Karkheh river basin in Iran to convert AMSR-E satellite SM product to daily rainfall at 10 meteorological stations. Good correlations R, ranging from 0.58–0.88, between the satellite-derived and the observed ground-based rainfall are obtained. Then, the SM2R-AMSRE rainfall are used as input into a previously calibrated-SWAT model to estimate the monthly river discharge at six gauging stations in the basin. Good agreement with the observations, with R²—values ranging between 0.72–0.87, are obtained, which is slightly less than the range obtained with the SWAT model using ground-based rainfall as input (R²~0.83–0.89). Indeed, there is a small but systematic underestimation of the SWAT- SM2R-AMSRE simulated streamflow, owing to the fact that the SM2R-AMSRE rainfall estimated with the SM2RAIN algorithm is also smaller than the ground-based one, which in turn, is due to the possibility of saturation of the satellite-retrieved soil moisture level. In spite of these restrictions, the overall good performance of the SM2RAIN algorithm for rainfall and river discharge (via SWAT) estimation in the Karkheh basin here opens new possibilities for discharge estimation throughout Iran, also by using more recent and more versatile satellite SM products, as started to be investigated by [62].

Furthermore, the two well-known TRMM-satellite-based rainfall products, TMPA-3B42 and TMPA-3B42RT, are assessed at the KRB climate stations after bias correction and compared with both ground-based and SM2E-AMSRE predictions. The results show that these TMPA-products predict the observed rainfall consistently less accurately than the SM2RAIN model. Similarly to SWAT- SM2R-AMSRE- simulated streamflow, the two TMPA-products are used as input into the previously calibrated-SWAT model. Expectedly, these SWAT-TMPA versions simulate the monthly runoff also less well than the SWAT- SM2R-AMSRE version, indicating again that using SM2R-AMSRE rainfall data in a hydrological model is a viable approach in basins with limited ground-based rainfall data.

The results of the present study indicate that with the use of AMSR-E SM products in the SM2RAIN algorithm as well as in the corrected version of TRMM satellite products, rainfall for poorly gauged regions can be fairly predicted. Moreover, these results show that physically based SM2RAIN model is at least in this application is more correlated with in-situ rainfall than TRMM rainfall satellite products that leads better prediction of runoff.

The methodology is applied to a watershed where the density of rain gauge stations is sparse, so conclusions from this study may provide evidence for the utilization of different rainfall and runoff estimation for water resources assessment of the KRB. The outputs of this study will help hydrologists to understand the efficiency and application of different rainfall estimation at the watershed scale.