Feasible Ways Promoting Nitrate Removal in Riparian Zone Downstream of a Regulated River
Abstract
:1. Introduction
2. Methods
2.1. Study Site
2.2. Modeling
2.2.1. Conceptual Model
2.2.2. Governing Equations
2.2.3. Numerical Model and Its Verification
2.2.4. Quantification of Biogeochemical Reaction
2.2.5. Model Scenarios
3. Results
3.1. Model Test
3.2. Biochemical Methods for Denitrifying
3.3. Hydrogeological Methods for Denitrifying
3.4. Topography Methods for Denitrifying
4. Discussion
4.1. Deficiency of the Model
4.2. Implications
4.2.1. Principles of Biochemical Denitrifying and Engineering Measures
4.2.2. Principles of Hydrogeological Denitrifying and Engineering Measures
4.2.3. Principles of Topography Denitrifying and Engineering Measures
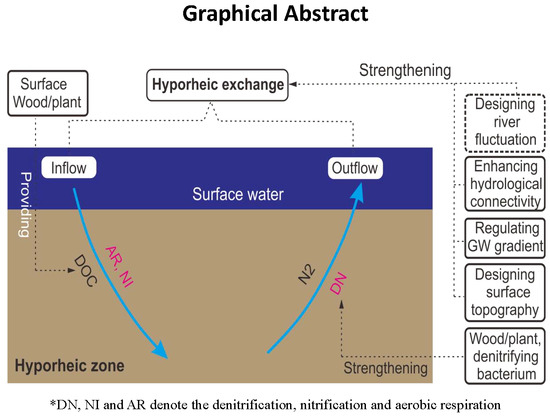
5. Conclusions
- (1)
- Increasing the DOC concentration of surface water and groundwater could largely increase the denitrifying amount in the riparian zone and accordingly increase the denitrifying efficiency. By comparison, adding denitrifying bacteria biomass had a smaller impact on the denitrifying amount, but it could improve the denitrifying rate to a great extent. The combined applications of these methods can make the denitrifying effect in the riparian zone “fast and good”.
- (2)
- Enhancing the hydrological connectivity of the aquifer surface could increase the denitrifying amount in the riparian zone to a certain extent, but the denitrifying efficiency was reduced correspondingly. By comparison, increasing the surface–groundwater hydraulic gradient had a much greater impact on the denitrifying amount, with the denitrifying efficiency reducing too. In practical applications, pumping the groundwater in the heavily polluted reach and cleaning the surface sedimentary sludge can effectively improve the denitrifying capacity in the riparian zone.
- (3)
- Designing the bank form into a concave shape could slightly increase the denitrifying amount in the riparian zone and correspondingly improve the denitrifying efficiency. By comparison, reducing the bank slope could largely increase the denitrifying amount and also improve the denitrifying efficiency. In practical applications, designing the bank form into a gentle slope with concave shape can improve the denitrifying capacity in the riparian zone to a certain extent.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Orghidan, T. Einneuer Lebensraum des unterirdischen Wassers: Der hyporheischeBiotop. Arch. Hydrobiol. 1959, 55, 392–414. [Google Scholar]
- Xia, J.; Chen, Y.; Wang, W.; Han, Y.; Liu, H.; Hu, L. Dynamic processes and ecological restoration of hyporheic layer in riparian zone. Adv. Water Sci. 2013, 24, 1–10. [Google Scholar]
- Bardini, L.; Boano, F.; Cardenas, M.B.; Revelli, R.; Ridolfi, L. Nutrient cycling in bedform induced hyporheic zones. Geochim. Cosmochim. Acta 2012, 84, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Cardenas, M.B. Stream-aquifer interactions and hyporheic exchange in gaining and losing sinuous streams. Water Resour. Res. 2009, 45, 267–272. [Google Scholar] [CrossRef]
- Daniele, T.; Buffington, J.M. Hyporheic exchange in gravel bed rivers with pool-riffle morphology: Laboratory experiments and three-dimensional modeling. Water Resour. Res. 2007, 430, 208–214. [Google Scholar]
- Hu, H.; Binley, A.; Heppell, C.M.; Lansdown, K.; Mao, X. Impact of microforms on nitrate transport at the groundwater-surface water interface in gaining streams. Adv. Water Resour. 2014, 73, 185–197. [Google Scholar] [CrossRef]
- Gu, C.; Anderson, W.; Maggi, F. Riparian biogeochemical hot moments induced by stream fluctuations. Water Resour. Res. 2012, 48, W09546. [Google Scholar] [CrossRef] [Green Version]
- Shuai, P.; Cardenas, M.B.; Knappett, P.S.K.; Bennett, P.C.; Neilson, B.T. Denitrification in the banks of fluctuating rivers: The effects of river stage amplitude, sediment hydraulic conductivity and dispersivity, and ambient groundwater flow. Water Resour. Res. 2017, 53, 7951–7967. [Google Scholar] [CrossRef]
- Trauth, N.; Musolff, A.; Knöller, K.; Kaden, U.S.; Keller, T.; Werban, U. River water infiltration enhances denitrification efficiency in riparian groundwater. Water Res. 2017, 130, 185–199. [Google Scholar] [CrossRef]
- Liu, D. Hyporheic Exchange and Solute Transport and Transformation Driven by Flood Wave; Hohai University: Nanjing, China, 2019. [Google Scholar]
- Hou, L.; Yin, G.; Liu, M.; Zhou, J.; Zheng, Y.; Gao, J.; Tong, C. Effects of sulfamethazine on denitrification and the associated N2O release in estuarine and coastal sediments. Environ. Sci. Technol. 2014, 49, 326–333. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Wu, Z. Coupling effect of pH and dissolved oxygen in water column on nitrogen release at water-sediment interface of Erhai Lake, China. Estuar. Coast. Shelf Sci. 2014, 149, 178–186. [Google Scholar] [CrossRef]
- Duff, J.H.; Triska, F.J. Denitrification in sediments from the hyporheic zone adjacent to a small forested stream. Can. J. Fish. Aquat. Sci. 2011, 47, 1140–1147. [Google Scholar] [CrossRef]
- Zarnetske, J.P.; Haggerty, R.; Wondzell, S.M.; Bokil, V.A.; González-Pinzón, R. Coupled transport and reaction kinetics control the nitrate source-sink function of hyporheic zones. Water Resour. Res. 2012, 48, W11508. [Google Scholar]
- Liu, D.; Zhao, J.; Chen, X.; Li, Y.; Feng, M. Dynamic processes of hyporheic exchange and temperature distribution in the riparian zone in response to dam-induced water fluctuations. Geosci. J. 2018, 22, 1–11. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, J.; Jeon, W.H.; Lee, J.Y. Solute dynamics across the stream-to-riparian continuum under different flood waves. Hydrol. Process. 2019, 33, 2627–2641. [Google Scholar] [CrossRef]
- Siergieiev, D.; Ehlert, L.; Reimann, T.; Lundberg, A.; Liedl, R. Modelling hyporheic processes for regulated rivers under transient hydrological and hydrogeological conditions. Hydrol. Earth Syst. Sci. 2015, 19, 329–340. [Google Scholar] [CrossRef] [Green Version]
- Voss, C.I. A finite element simulation model for saturated-unsaturated, fluid-density-dependent groundwater flow with energy transport or chemically reactive single-species solute transport. Water Resour. Investig. Rep. (USA) 1984, 84, 4369. [Google Scholar]
- Reeves, H.W.; Thibodeau, P.M.; Underwood, R.G.; Gardner, L.R. Incorporation of total stress changes into the ground water model SUTRA. Groundwater 2000, 38, 89–98. [Google Scholar] [CrossRef]
- Gardner, L.R.; Wilson, A.M. Comparison of four numerical models for simulating seepage from salt marsh sediments. Estuar. Coast. Shelf Sci. 2006, 69, 427–437. [Google Scholar] [CrossRef]
- Boutt, D.F. Poroelastic loading of an aquifer due to upstream dam releases. Groundwater 2010, 48, 580–592. [Google Scholar] [CrossRef]
- Molz, F.J.; Widdowson, M.A.; Benefield, L.D. Simulation of microbial growth dynamics coupled to nutrient and oxygen transport in porous media. Water Resour. Res. 1986, 22, 1207–1216. [Google Scholar] [CrossRef]
- Diersch, H.J. Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer: Berlin, Germany, 2014; p. 996. [Google Scholar]
- Schenk, O.; Gärtner, K. Solving unsymmetric sparse systems of linear equations with pardiso. Future Gener. Comput. Syst. 2004, 20, 475–487. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef] [Green Version]
- Fetter, C. Applied Hydrogeology, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2000; p. 598. [Google Scholar]
- Schulze-Makuch, D. Longitudinal dispersivity data and implications for scaling behavior. Groundwater 2005, 43, 443–456. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.S.; Lee, K.K.; Hyun, Y.; Clement, T.P.; Hamilton, D. Nitrogen transformation and transport modeling in groundwater aquifers. Ecol. Model. 2006, 192, 143–159. [Google Scholar] [CrossRef] [Green Version]





| Method | Particle Diameter Analysis (Hazen Method) | Indoor Darcy Penetration Test | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | |
| Hydraulic conductivity (m/day) | 228.1 | 113.2 | 169.3 | 104.5 | 88.1 | 120.1 |
| Case | DOC Concentration of Surface Water (CSTR-DOC, mg/L) | DOC Concentration of Groundwater (CGW-DOC, mg/L) | Biomass Concentration of Denitrifying Bacteria (XDN, mg/L) | Hydraulic Conductivity of Saturated Aquifer (K, m/day) | Surface Water–Groundwater Hydraulic Gradient (i, -) | Bank Slope (, °) | Convex Distance (d1, m) | Concave Distance (d2, m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 0 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 2 | 10 | 0 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 3 | 15 | 0 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 4 | 5 | 0 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 5 | 5 | 5 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 6 | 5 | 10 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 7 | 5 | 0 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 8 | 5 | 0 | 2 | 43.2 | 0 | 45 | 0 | 0 |
| 9 | 5 | 0 | 4 | 43.2 | 0 | 45 | 0 | 0 |
| 10 | 5 | 0 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 11 | 5 | 0 | 1 | 86.4 | 0 | 45 | 0 | 0 |
| 12 | 5 | 0 | 1 | 129.6 | 0 | 45 | 0 | 0 |
| 13 | 5 | 0 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 14 | 5 | 0 | 1 | 43.2 | 0.0025 | 45 | 0 | 0 |
| 15 | 5 | 0 | 1 | 43.2 | 0.005 | 45 | 0 | 0 |
| 16 | 5 | 0 | 1 | 43.2 | 0 | 30 | 0 | 0 |
| 17 | 5 | 0 | 1 | 43.2 | 0 | 45 | 0 | 0 |
| 18 | 5 | 0 | 1 | 43.2 | 0 | 60 | 0 | 0 |
| 19 | 5 | 0 | 1 | 43.2 | 0 | 45 | 0 | - |
| 20 | 5 | 0 | 1 | 43.2 | 0 | 45 | 0.73 | - |
| 21 | 5 | 0 | 1 | 43.2 | 0 | 45 | 1.46 | - |
| 22 | 5 | 0 | 1 | 43.2 | 0 | 45 | - | 0 |
| 23 | 5 | 0 | 1 | 43.2 | 0 | 45 | - | −0.73 |
| 24 | 5 | 0 | 1 | 43.2 | 0 | 45 | - | −1.46 |
| Parameters | Input Values | Units |
|---|---|---|
| Flow parameters | ||
| Hydraulic conductivity of the saturated zone (K) a | 43.2 | m/day |
| Effective porosity (ne) a | 0.4 | - |
| Specific storage (S0) b | 0.0001 | 1/m |
| Residual saturation (sr) b | 0.15 | - |
| Maximum saturation (ss) b | 1 | - |
| The parameter of VG model () b | 7 | 1/m |
| The parameter of VG model (n) b | 1.89 | - |
| Longitudinal dispersivity (DL) c | 1 | m |
| Transverse/longitudinal dispersivity (DT/DL) c | 0.1 | - |
| Solute and biogeochemical parameters | ||
| The O2 concentration of surface water a | 5 | mg/L |
| The NH4+ concentration of surface water d | 0.05 | mg/L |
| The NO3− concentration of surface water d | 5 | mg/L |
| The DOC concentration of surface water a | 5 | mg/L |
| The NH4+ and NO3− concentration of groundwater d | 0 | mg/L |
| The DOC concentration of groundwater a | 0 | mg/L |
| The O2 concentration of groundwater a | 2 | mg/L |
| Maximum specific uptake rate for AR (UAR) e,f,g | 2 | mg/L/d |
| Maximum specific uptake rate for NI (UNI) e | 1.05 | mg/L/d |
| Maximum specific uptake rate for DN (UDN) e,f,g | 2 | mg/L/d |
| Half saturation constant for O2 (KO2) e,f,g | 1 | mg/L |
| Half saturation constant for NH4+ (KNH4) e,f | 0.5 | mg/L |
| Half saturation constant for NO3− (KNO3) e,f,g | 1 | mg/L |
| Half saturation constant for DOC (KDOC) e,f,g | 5 | mg/L |
| O2 inhibition constant (KI) e,f | 1 | mg/L |
| O2 partition coefficient (yO2) e | 0.64 | - |
| Case | CSTR-DOC (mg/L) | CGW-DOC (mg/L) | XDN (mg/L) | Min-NO3 (g) | Mrem-NO3 (g) | Nrem-NO3 (-) |
|---|---|---|---|---|---|---|
| 1 | 5 | 0 | 1 | 40.90 | 6.34 | 15.5% |
| 2 | 10 | 0 | 1 | 40.90 | 16.36 | 40.0% |
| 3 | 15 | 0 | 1 | 40.90 | 22.70 | 55.5% |
| 4 | 5 | 0 | 1 | 40.90 | 6.34 | 15.5% |
| 5 | 5 | 5 | 1 | 40.90 | 19.01 | 46.5% |
| 6 | 5 | 10 | 1 | 40.90 | 22.23 | 54.5% |
| 7 | 5 | 0 | 1 | 40.90 | 6.34 | 15.5% |
| 8 | 5 | 0 | 2 | 40.90 | 9.41 | 23.0% |
| 9 | 5 | 0 | 4 | 40.90 | 11.38 | 27.8% |
| Case | K (m/day) | i (-) | Qmax (m2) | Min-NO3 (g) | Mrem-NO3 (g) | Nrem-NO3 (-) |
|---|---|---|---|---|---|---|
| 10 | 43.2 | 0 | 6.2 | 40.90 | 6.34 | 15.5% |
| 11 | 86.4 | 0 | 9.0 | 55.67 | 7.56 | 13.6% |
| 12 | 129.6 | 0 | 11.1 | 66.75 | 8.46 | 12.7% |
| 13 | 43.2 | 0 | 6.2 | 40.90 | 6.34 | 15.5% |
| 14 | 43.2 | 0.0025 | 26.5 | 144.71 | 21.27 | 14.7% |
| 15 | 43.2 | 0.005 | 50.3 | 263.92 | 35.89 | 13.6% |
| Case | (°) | d1 (m) | d2 (m) | Qmax (m2) | Min-NO3 (g) | Mrem-NO3 (g) | Nrem-NO3 (-) |
|---|---|---|---|---|---|---|---|
| 16 | 30 | 0 | 0 | 6.23 | 42.30 | 7.03 | 16.6% |
| 17 | 45 | 0 | 0 | 6.20 | 40.90 | 6.34 | 15.5% |
| 18 | 60 | 0 | 0 | 6.07 | 40.12 | 6.00 | 14.9% |
| 19 | 45 | 0 | - | 6.20 | 40.90 | 6.34 | 15.5% |
| 20 | 45 | 0.73 | - | 6.16 | 40.23 | 6.12 | 15.2% |
| 21 | 45 | 1.46 | - | 6.11 | 39.38 | 5.89 | 14.7% |
| 22 | 45 | - | 0 | 6.20 | 40.90 | 6.34 | 15.5% |
| 23 | 45 | - | −0.73 | 6.22 | 41.91 | 6.60 | 15.7% |
| 24 | 45 | - | −1.46 | 6.24 | 42.31 | 6.77 | 16.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhu, B.; Zhu, H.; Zhao, J. Feasible Ways Promoting Nitrate Removal in Riparian Zone Downstream of a Regulated River. Water 2020, 12, 2054. https://doi.org/10.3390/w12072054
Liu D, Zhu B, Zhu H, Zhao J. Feasible Ways Promoting Nitrate Removal in Riparian Zone Downstream of a Regulated River. Water. 2020; 12(7):2054. https://doi.org/10.3390/w12072054
Chicago/Turabian StyleLiu, Dongsheng, Bei Zhu, Haoyu Zhu, and Jian Zhao. 2020. "Feasible Ways Promoting Nitrate Removal in Riparian Zone Downstream of a Regulated River" Water 12, no. 7: 2054. https://doi.org/10.3390/w12072054
APA StyleLiu, D., Zhu, B., Zhu, H., & Zhao, J. (2020). Feasible Ways Promoting Nitrate Removal in Riparian Zone Downstream of a Regulated River. Water, 12(7), 2054. https://doi.org/10.3390/w12072054