TIEOF: Algorithm for Recovery of Missing Multidimensional Satellite Data on Water Bodies Based on Higher-Order Tensor Decompositions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Multi-Way Tensor Decompositions
2.2. Interpolation on a Static Rectangular Grid
2.3. Data Thresholding
2.4. Validation Dataset
2.5. Missing Data Reconstruction
| Algorithm 1 TIEOF |
|
2.6. The Lake Baikal Dataset
3. Results
3.1. Interpolation on a Rectangular Grid
3.2. Effect of Early Stopping
3.3. Data Thresholding Reduces Reconstruction Errors
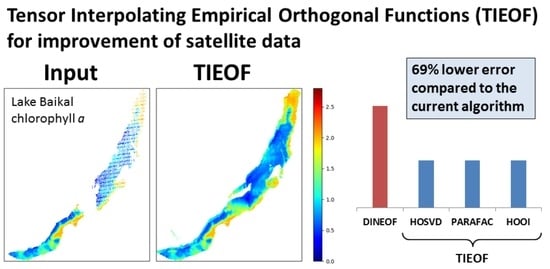
3.4. Comparison of the Tensor Decomposition Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALS | Alternating Least Squares |
| DINEOF | Data Interpolating Empirical Orthogonal Functions |
| EOF | Empirical Orthogonal Functions |
| HOOI | Higher Order Orthogonal Iteration |
| HOSVD | Truncated Higher Order Singular Value Decomposition |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NRMSE | Normalized Root Mean Squared Error |
| PARAFAC | Parallel Factors |
| PCA | Principal component analysis |
| SeaWiFS | Sea-Viewing Wide Field-of-View Sensor |
| SVD | Singular Value Decomposition [NI](SVD) |
| TIEOF | Tensor Interpolating Empirical Orthogonal Functions |
References
- Crétaux, J.F.; Abarca-del Río, R.; Berge-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake volume monitoring from space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef] [Green Version]
- Ganzedo, U.; Alvera-Azcarate, A.; Esnaola, G.; Ezcurra, A.; Saenz, J. Reconstruction of sea surface temperature by means of DINEOF: A case study during the fishing season in the Bay of Biscay. Int. J. Remote Sens. 2011, 32, 933–950. [Google Scholar] [CrossRef]
- Bergamino, N.; Horion, S.; Stenuite, S.; Cornet, Y.; Loiselle, S.; Plisnier, P.D.; Descy, J.P. Spatio-temporal dynamics of phytoplankton and primary production in Lake Tanganyika using a MODIS based bio-optical time series. Remote Sens. Environ. 2010, 114, 772–780. [Google Scholar] [CrossRef]
- Breece, M.W.; Oliver, M.J.; Fox, D.A.; Hale, E.A.; Haulsee, D.E.; Shatley, M.; Bograd, S.J.; Hazen, E.L.; Welch, H. A satellite-based mobile warning system to reduce interactions with an endangered species. Ecol. Appl. 2021, 31, e02358. [Google Scholar] [CrossRef] [PubMed]
- Pigott, T.D. A Review of Methods for Missing Data. Educ. Res. Eval. 2001, 7, 353–383. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, J.G.; Molenberghs, G. Missing data methods in longitudinal studies: A review. Test 2009, 18, 1–43. [Google Scholar] [CrossRef] [Green Version]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Vienna, Austria, 2019; Volume 793. [Google Scholar]
- Kamakura, W.A.; Wedel, M. Factor analysis and missing data. J. Mark. Res. 2000, 37, 490–498. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Zeng, C.; Li, X.; Wei, Y. Missing data reconstruction in remote sensing image with a unified spatial–temporal–spectral deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef] [Green Version]
- Jaques, N.; Taylor, S.; Sano, A.; Picard, R. Multimodal autoencoder: A deep learning approach to filling in missing sensor data and enabling better mood prediction. In Proceedings of the 2017 Seventh International Conference on Affective Computing and Intelligent Interaction (ACII), San Antonio, TX, USA, 23–26 October 2017; pp. 202–208. [Google Scholar]
- Beckers, J.M.; Rixen, M. EOF calculations and data filling from incomplete oceanographic datasets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Ilin, A.; Raiko, T. Practical approaches to principal component analysis in the presence of missing values. J. Mach. Learn. Res. 2010, 11, 1957–2000. [Google Scholar]
- Wiberg, T. Umea, Computation of Principal Components when Data are Missing. Proc. Second Symp. Comput. Stat. 1976, 229–236. [Google Scholar]
- Grung, B.; Manne, R. Missing values in principal component analysis. Chemom. Intell. Lab. Syst. 1998, 42, 125–139. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern recognition. Mach. Learn. 2006, 128, 580–583. [Google Scholar]
- Sidiropoulos, N.D.; De Lathauwer, L.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Hitchcock, F.L. The expression of a tensor or a polyadic as a sum of products. J. Math. Phys. 1927, 6, 164–189. [Google Scholar] [CrossRef]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef] [Green Version]
- UNESCO World Heritage Centre: Lake Baikal. Available online: https://whc.unesco.org/en/list/754 (accessed on 1 September 2021).
- Namsaraev, Z.; Melnikova, A.; Ivanov, V.; Komova, A.; Teslyuk, A. Cyanobacterial bloom in the world largest freshwater lake Baikal. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 121, p. 032039. [Google Scholar]
- Cichocki, A.; Mandic, D.; De Lathauwer, L.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H.A. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef] [Green Version]
- Sidiropoulos, N.D.; Bro, R.; Giannakis, G.B. Parallel factor analysis in sensor array processing. IEEE Trans. Signal Process. 2000, 48, 2377–2388. [Google Scholar] [CrossRef] [Green Version]
- Vasilescu, M.A.O.; Terzopoulos, D. Multilinear analysis of image ensembles: Tensorfaces. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2002; pp. 447–460. [Google Scholar]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1227–1243. [Google Scholar] [CrossRef] [Green Version]
- Cong, F.; Lin, Q.H.; Kuang, L.D.; Gong, X.F.; Astikainen, P.; Ristaniemi, T. Tensor decomposition of EEG signals: A brief review. J. Neurosci. Methods 2015, 248, 59–69. [Google Scholar] [CrossRef] [Green Version]
- Hamdi, S.M.; Wu, Y.; Boubrahimi, S.F.; Angryk, R.; Krishnamurthy, L.C.; Morris, R. Tensor decomposition for neurodevelopmental disorder prediction. In International Conference on Brain Informatics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 339–348. [Google Scholar]
- Hore, V.; Viñuela, A.; Buil, A.; Knight, J.; McCarthy, M.I.; Small, K.; Marchini, J. Tensor decomposition for multiple-tissue gene expression experiments. Nat. Genet. 2016, 48, 1094–1100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McNeice, G.W.; Jones, A.G. Multisite, multifrequency tensor decomposition of magnetotelluric data. Geophysics 2001, 66, 158–173. [Google Scholar] [CrossRef]
- Franz, T.; Schultz, A.; Sizov, S.; Staab, S. Triplerank: Ranking semantic web data by tensor decomposition. In International Semantic Web Conference; Springer: Berlin/Heidelberg, Germany, 2009; pp. 213–228. [Google Scholar]
- Anandkumar, A.; Ge, R.; Hsu, D.; Kakade, S.M.; Telgarsky, M. Tensor decompositions for learning latent variable models. J. Mach. Learn. Res. 2014, 15, 2773–2832. [Google Scholar]
- Carroll, J.D.; Chang, J.J. Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition. Psychometrika 1970, 35, 283–319. [Google Scholar] [CrossRef]
- Harshman, R. Foundations of the PARAFAC Procedure: Models and Conditions for an “Explanatory" Multi-Modal Factor Analysis; UCLA Working Papers in Phonetics; University of California: Los Angeles, CA, USA, 1970. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Kroonenberg, P.M.; De Leeuw, J. Principal component analysis of three-mode data by means of alternating least squares algorithms. Psychometrika 1980, 45, 69–97. [Google Scholar] [CrossRef]
- Rabanser, S.; Shchur, O.; Günnemann, S. Introduction to Tensor Decompositions and their Applications in Machine Learning. arXiv 2017, arXiv:1711.10781. [Google Scholar]
- Sheehan, B.; Saad, Y. Higher Order Orthogonal Iteration of Tensors (HOOI) and Its Relation to PCA and GLRAM. In Proceedings of the 2007 SIAM International Conference on Data Mining (SDM); 2007; Available online: https://epubs.siam.org/doi/10.1137/1.9781611972771.32 (accessed on 14 September 2021).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine Learning in Python. arXiv 2018, arXiv:1201.0490. [Google Scholar]
- Heim, B. Qualitative and Quantitative Analyses of Lake Baikal’s Surface-Waters Using Ocean Colour Satellite Data (SeaWiFS). Ph.D. Thesis, Universität Potsdam, Potsdam, Germany, 2005. [Google Scholar]
- Abbas, M.M.; Melesse, A.M.; Scinto, L.J.; Rehage, J.S. Satellite Estimation of Chlorophyll-a Using Moderate Resolution Imaging Spectroradiometer (MODIS) Sensor in Shallow Coastal Water Bodies: Validation and Improvement. Water 2019, 11, 1621. [Google Scholar] [CrossRef] [Green Version]
- Hooker, S.B.; Firestone, E.R.; OReilly, J.E.; Maritorena, S.; OBrien, M.C.; Siegel, D.A.; Toole, D.; Mueller, J.L.; Mitchell, B.G.; Kahru, M.; et al. Postlaunch Calibration and Validation Analyses; SeaWiFS Postlaunch Technical Report Series; Goddard Space Flight Center: Greenbelt, MD, USA, 2000; Volume 11. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Wall, M.; Rechtsteiner, A.; Rocha, L. Singular Value Decomposition and Principal Component Analysis. In A Practical Approach to Microarray Data Analysis; Springer: Boston, MA, USA, 2002; Volume 5. [Google Scholar] [CrossRef] [Green Version]
- Prechelt, L. Early stopping-but when. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar]
- Claus, S.; De Hauwere, N.; Vanhoorne, B.; Deckers, P.; Souza Dias, F.; Hernandez, F.; Mees, J. Marine regions: Towards a global standard for georeferenced marine names and boundaries. Mar. Geod. 2014, 37, 99–125. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Hui, Z.; Gao, X.; Yang, Y.; Wang, X. Lightweight Image Super-Resolution with Information Multi-distillation Network. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019. [Google Scholar] [CrossRef] [Green Version]
- Hilborn, A.; Costa, M. Applications of DINEOF to satellite-derived chlorophyll-a from a productive coastal region. Remote Sens. 2018, 10, 1449. [Google Scholar] [CrossRef] [Green Version]










| Method | Improvement Factor |
|---|---|
| DINEOF | 1.24 |
| TIEOF: HOSVD | 1.56 |
| TIEOF: PARAFAC | 1.56 |
| TIEOF: HOOI | 1.57 |
| Data | Method | Mean NRMSE |
|---|---|---|
| AQUA | DINEOF | 0.68 |
| TIEOF: HOSVD | 0.48 | |
| TIEOF: PARAFAC | 0.48 | |
| TIEOF: HOOI | 0.47 | |
| TERRA | DINEOF | 0.74 |
| TIEOF: HOSVD | 0.51 | |
| TIEOF: PARAFAC | 0.51 | |
| TIEOF: HOOI | 0.50 | |
| SEAWIFS | DINEOF | 1.93 |
| TIEOF: HOSVD | 0.90 | |
| TIEOF: PARAFAC | 0.90 | |
| TIEOF: HOOI | 0.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulikov, L.; Inkova, N.; Cherniuk, D.; Teslyuk, A.; Namsaraev, Z. TIEOF: Algorithm for Recovery of Missing Multidimensional Satellite Data on Water Bodies Based on Higher-Order Tensor Decompositions. Water 2021, 13, 2578. https://doi.org/10.3390/w13182578
Kulikov L, Inkova N, Cherniuk D, Teslyuk A, Namsaraev Z. TIEOF: Algorithm for Recovery of Missing Multidimensional Satellite Data on Water Bodies Based on Higher-Order Tensor Decompositions. Water. 2021; 13(18):2578. https://doi.org/10.3390/w13182578
Chicago/Turabian StyleKulikov, Leonid, Natalia Inkova, Daria Cherniuk, Anton Teslyuk, and Zorigto Namsaraev. 2021. "TIEOF: Algorithm for Recovery of Missing Multidimensional Satellite Data on Water Bodies Based on Higher-Order Tensor Decompositions" Water 13, no. 18: 2578. https://doi.org/10.3390/w13182578
APA StyleKulikov, L., Inkova, N., Cherniuk, D., Teslyuk, A., & Namsaraev, Z. (2021). TIEOF: Algorithm for Recovery of Missing Multidimensional Satellite Data on Water Bodies Based on Higher-Order Tensor Decompositions. Water, 13(18), 2578. https://doi.org/10.3390/w13182578