1. Introduction
1.1. Modelling of the River Floods
River floods can be considered as a crucial type of dangerous event. The damage caused by a river flood may reach hundreds of thousands of dollars [
1,
2]. Moreover, natural hazards take lives and affect a large number of people every year [
3]. Because it is vital to predicting such floods successfully, there are a lot of scientific works dedicated to flooding operational modeling based on various solutions [
4].
To reduce the damage caused by natural disasters, forecasting systems are used. They are based on models that predict water levels and flow rates. Classical methods used in hydrology are based on determining the dependence between meteorological data, basin and substrate characteristics, and modeled target values [
5]. There are widely used approaches to modeling nature processes, which were implemented in the form of hydrological models. Such models mainly rely on the deterministic approach, but some models operate with elements of stochastic nature [
6]. It allows us to reproduce a wide class of processes with suitable hydrological models. The advantage of such models is that they are can be well interpreted by experts [
7]. Most models are not implemented for a specific region but represent the bonds between the components of almost any river system.
Model calibration is used to take into account the specific characteristics of a particular region [
8]. Adapting the model to the desired domain allows reducing forecast error. However, for complex models, calibration can be too complicated and computationally expensive. Moreover, complex physical models require a lot of data that may not exist or may not be insufficient quantity for the modeled river basin. Due to the difficulties with calibration, the application of such models becomes inefficient in some cases [
9].
Another way of physical modeling for flood prediction is explaining flow patterns through differential equations. The disadvantages of the equation-based models are the unstable solutions caused by errors accumulation [
10] and high computational and algorithmic requirements. Moreover, such approaches may be challenging to generalize to other rivers and basins, for which they require the addition of new parameters.
To take local effects into account, data-driven approaches based on machine learning (ML) methods can be used [
11]. They are less interpretable but can produce high-quality forecasts [
12]. On the other hand, complex machine learning models, such as neural networks, require a lot of data to train.
To account for the advantages of physical models (interpretability) and machine learning models (low forecasting error), ensembling is used [
13]. Such hybrid models allow for a refinement of predictions derived from hydrological models [
14] using ML techniques. To improve such multi-level forecasting models data fusion methods [
15] can be used. Such approaches based on the ensemble of different models (machine learning- and physics-based) are becoming more popular in the design of predictive systems. Also, the perspective approach that allows to train and calibrate models differently for each data source can be proposed. In that case, distortions and errors in one source cannot lead to critical errors in the whole system [
16]. Unfortunately, such complex hybrid pipelines are hard to identify and configure.
To simplify the identification task, automated machine learning (AutoML) can be applied. Methods and algorithms of AutoML are devoted to automated identification and tuning of ML models. A main concept of the AutoML approach is the building of ML models without the involvement of an expert or with their minimal involvement. However, most of the existing AutoML tools cannot be used to obtain heterogeneous (composite) pipelines, that combined models of different nature (for example, ML models and hydrological models). At the same time, composite modeling is especially promising for flood forecasting since it allows combining the state-of-the-art data-driven and physics-based methods and models according to the Composite Artificial Intelligence concepts [
17].
In the paper, we propose an automated approach for short-term flood forecasting. The approach is based on the application of automated machine learning, composite models (pipelines), and data fusion. Application of the various data sources (meteorological, hydrological, and remote sensing measurements) in combination with automated identification and calibration of the models make it possible to construct composite pipelines. Machine learning methods are used to forecast time series of daily water levels. Short-term prediction of this variable allows us to avoid negative effects from its rapid increase through prompt decision-making. Involvement of the physical models allows improving the interpretability of the final pipeline. This solution can be used for the analysis of the river’s condition.
1.2. Existing Methods and Models for Flood Forecasting
In this subsection we are analyzing the most significant causes of floods and the specific features of the Lena River basin, which do not allow to apply of existing approaches for flood modeling in this area.
Siberia region floods are of interest to researchers because of their destructive power and annual occurrence [
18,
19]. Regarding the Lena River, its condition has been studied and modeled by researchers as classical methods of expert search for dependencies between the components of the system [
20] as numerical methods. Because the river flows in a cold climate, most of the year channels are covered with ice and snow. So numerical models for this region are created to assess both ice conditions [
21] and channel changes during the ice-free period [
22].
The major difficulty in modeling floods on the Lena river is in a high variety of flood causes. The largest floods occur when the superposition of several factors of water level rise at once: a regular rise associated with melting snow in spring and extreme rises in from ice-jam. It is difficult to predict such floods on the basis of snowmelt or on retrospective statistical information alone.
Based on an extensive literature review [
23], we can consider the following causes of river flooding (most relevant for the Lena river):
For the Lena River basin, flooding in the spring period is most typical due to snow melting, precipitation and a high probability of ice-jam formation [
28]. The following ways of modeling each type of flood are presented in
Table 1.
As can be seen from the table, there are several approaches that can be suitable for Lena River floods forecasting. Nevertheless, each of them has disadvantages that do not allow to use of only one method. Therefore, we decided to build a composite model (pipeline) based on several blocks. Each of the individual blocks is modeling the desired component of the flood.
It is worth adding that the frequency of occurrence of each cause is different [
40]. The rise in water levels associated with melting snow can be attributed to regular (annual) phenomena. At the same time, conditions associated with high precipitation and the formation of ice jams are non-periodic. Such causes are highly dependent on the synoptic situation in the region. In addition, the precipitation field is spatially heterogeneous, which makes it impossible to predict the average increase in water at all hydro gauges. Precipitation may cause localized increases in water levels in some parts of the river due to different rainfall intensities and soil characteristics. The same problem exists for ice-jam floodings. The rise of the level at a specific level gauge not always leads to an increase in the level at the neighboring ones. So, it becomes extremely important to consider local features not only for the basin but for specific sections of the river and watersheds.
The second important factor is the remoteness of the Lena River from major cities. The river basin is very large, and at the same time, the number of hydro gauges is not high enough. For this reason, the models that are based on remote sensing data are often used for flood forecasting on the Lena River [
41]. A widespread method is the application of models or manual interpretation to remote sensing data for the tasks of detecting and predicting river spills. The example is presented in article [
42], which demonstrates the calculation of a set of river state parameters, such as discharge, propagation speed, and hydraulic geometry with Moderate Resolution Imaging Spectroradiometer (MODIS) satellite imagery. Also, Landsat satellite images were used for monitoring the spatial and temporal extent of spring floods [
43] on the Lena River. Also, remote sensing data are calibrated with in situ observations [
44,
45], which allows supplementing the data. The context of such works implies the detection of the current state of the river. The emphasis on predictive models is usually not made. Numerical models allow reproduction of the state of a watercourse at any period of time, based on some input set of actual data.
We can conclude that the rise in water levels in the Lena River depends on many factors. Each of these causes contributes to the overall increase in the level at all hydro gauges on the river, as well as at only some of them. In the paper, we refer to the floods that are caused by a combination of several causes as multi-causes flooding. For example, when the water level rises due to both snow melting and the ice-jams formation. Successfully managing all of these factors requires a comprehensive approach. The described approaches are (1) too complicated to prepare and calibrate, or (2) do not take all crucial flood causes into account. Therefore, in the proposed approach we design an ensemble of several models to combine the advantages of different methods in a single composite pipeline. The novelty of this approach is the automatic identification of individual blocks in the predictive system, as well as the hybridization of models for multi-causes flood forecasting.
Each of the individual blocks in the pipeline is designed to predict a flood based on one or several of the described causes. Each block is specialized to reproduce the required patterns from the provided data only. The simulation blocks can be physical models as well as ML models. Since the identification and tuning of ML models requires the involvement of an expert and takes a lot of time, special algorithms for automation are used. The proposed AutoML approach is based on the evolutionary algorithm for identifying ML models. It allows to automatically identify models, tune hyperparameters, and combine stand-alone models into ensembles. Moreover, the optimal ML model structure search process is designed in such a way that can simplify the structure of the pipelines. This allows obtaining stand-alone models as the final solution if that is sufficient for successful forecasting. In addition, modern AutoML solutions have already shown their high accuracy compared to stand-alone models [
46]. It also makes the approach more flexible, since identifying individual blocks becomes possible without involving an expert. Consequently, the forecasting system is easier to transfer to new basins and rivers if AutoML algorithms are used.
We validated this approach on the Lena River basin. Floods in this territory are an actively and sufficiently studied common occurrence. Such phenomenon is annual and directly depends on runoff factors also including ice-jam formations [
18]. For this reason, the analysed area is a suitable for the validation of constructing multi-causes flood system.
The paper is organized as follows.
Section 1 contains the description of the existing approach for flood forecasting.
Section 2 described the different aspects of the proposed automated approach and validation methods.
Section 3 provides the extensive experimental validation of the proposed approach for the Lena River case study;
Section 4 described the main limitation of the study and obtained insight. Finally,
Section 5 summarizes the achieved results and provides references to the code and data used in the paper.
2. Materials and Methods
2.1. Input Data for Case Study
The input data for modeling and validation are provided by The Russian Federal Service for Hydrometeorology and Environmental Monitoring and Federal Agency of Water Resources [
47,
48]. For both physical modeling and the machine learning approach, data from hydro gauges and weather stations were used. Locations of stations and zone of interest are shown in
Figure 1.
The Lena River is located in Eastern Russia. The area of the basin is 2,430,000 km
[
49]. This region can be characterized by a Siberian climate with extremely low temperatures during winter. The river flows entirely in permafrost conditions [
50] from south to north, which is increasing the probability of ice-jam flooding during spring periods [
28,
51]. As was mentioned earlier, the following causes of spring floodwater on the Lena River include: [
28]:
Large amounts of precipitation during autumn;
Low temperatures during winter with extensive accumulation of snow;
Early prosperous spring with rapid increasing of daily temperature;
Heavy precipitation during snowmelt.
The rise in the water level, as well as the increase in flow, typically occurs during the beginning of May to mid-July (
Figure 2).
The successful prediction of extreme water level rises requires using not only the prehistory of water level but also information from weather stations and date and time values. It is also vital to aggregate the features for the previous periods which show the conditions in which the snow cover formed in the river basin, etc. To get the most complete and operational information about the modeled basin, various data sources (tables, time series, images) were used:
Water levels at gauging stations in the form of time series with daily time resolution;
Meteorological parameters measured near the level gauging stations and additional information about the events at the river;
Meteorological parameters from weather stations. Time resolution for parameters may differ from three hours to daily. This data refers to points located at some distance from level gauging stations;
Additional information, derived from open sources, such as remote sensing data from MODIS sensor.
Parameters that were recorded at the weather stations and hydro gauges are shown in
Table 2.
Remote sensing data from the MODIS sensor was used as an additional data source to train the physical model. If necessary, interpolation and gap-filling were applied to the values of the meteorological parameters from tables.
2.2. Composite Modelling Approach
Composite models (pipelines) show strong predictive performance when processing different types of data [
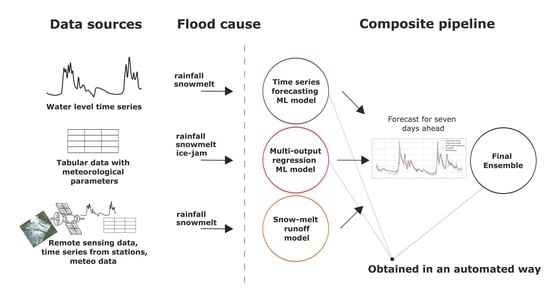
52]. Therefore, to build a precise and at the same time robust model, it was decided to use a composite approach with automatic machine learning techniques and evolutionary computing. Each of the composite pipeline blocks was compiled either completely using automatic model design generation or using optimization algorithms for block (model) calibration. We propose to build a composite flood forecasting model consisting of three blocks:
Machine learning model for time series forecasting. Predictions of such a model based on time series of water levels. The number of such models equals the number of gauging stations;
Machine learning model for multi-output regression. Predictions of such a model based on meteorological conditions. The number of such models equals the number of gauging stations;
Snowmelt-Runoff Model. The physical model is implemented and configured for the most critical level gauges;
The target variable for such a system to predict is the maximum daily water level. The configuration of the final model together with the model blocks can be seen in
Figure 3.
The pipeline presented in
Figure 3 allows using as much data as possible. The primary reason to use an ensemble in a composite pipeline is a reduction of forecast error compared to stand-alone models [
53]. Also, it allows specialization of individual blocks of the composite ensemble to solve the utilitarian task.
As an example, the multi-output regression model predicts water levels based on mostly meteorological data. The time series forecasting model predicts only on the basis of previous level values using autoregressive dependencies. Then, if incorrect values of meteorological parameters are obtained and the multi-output regression model is producing incorrect forecasts, the time series forecasting model still can preserve the stability of the ensemble. The use of the physical model makes it possible to interpret the forecast.
Therefore, if any of the models produce an unrealistic result, the expert can refer to the snow-melt runoff model on the critical (main) gauging station and check the adequacy of the system output.
Another advantage of the composite approach is its robustness - not only to distorted measurements, but also to the lack of data sources. If multiple data sources exist, it is possible to re-configure the pipeline and use the blocks with available input data only.
Individual blocks based on machine learning models are identified using the evolutionary algorithm for automatic machine learning described in the paper [
52]. Then, the ensembling was used to combine the predictions of the individual blocks in the composite pipelines. Most solutions with using model ensembling are aimed at ensuring that the ensemble is “sufficiently diverse”. Therefore, the errors of individual algorithms on particular objects will be compensated for by other algorithms. When building an ensemble, the main task is to improve the quality of modeling of basic algorithms and increasing the diversity of basic algorithms. This effect is achieved through the following methods: changing the volume of the training data set, target vector, or set of basic models. In this paper, the Random Forest model was used as meta-algorithm for ensembling. The predictors were the following: the predictions of the individual blocks, month and day. Next, a general scheme for optimizing the resulting ensemble is applied. The rationale for using the meta-algorithm is the fact that an ensemble can represent a significantly more complex function than any basic algorithm in many cases. So, ensembles allow us to solve complex problems with simple models. The effective adjustment of these models to the data occurs at the level of a meta-algorithm.
To find the optimal hyperparameters values for the ensemble model we apply Bayesian optimization [
54]. The Bayesian optimization is a modification of random search optimization. The main idea is to choose the best area of the hyperparameter space, based on taking into account the history of the points at which the models were trained and the values of the objective function were obtained. This hyperparameter optimization method contains two key blocks: a probabilistic surrogate model and an acquisition function for the next point. We can consider this as an ordinary usual machine learning task, where the selection function is a quality function for the meta-algorithm used in Bayesian hyperparameter optimization, and the surrogate model is the model that we get at the output of this meta-algorithm. The widely-used functions are Expected Improvement, Probability of Improvement, and, for surrogate models, Gaussian Processes (GP) and Tree-Structured Parzen Estimators (TPE) [
55]. At each iteration, the surrogate model is trained for all previously obtained outputs and tries to get a simpler approximation of the objective function. Next, the selection function evaluates the “benefit” of the various following points using the predictive distribution of the surrogate model. It balances between the use of already available information and the “exploration” of a new area of space.
2.3. Data Preprocessing
Qualitative preparation of data before fitting the machine learning models or calculating physical models provides the greatest possibility to improve the result of prediction.
As was mentioned before, the primary data set contains observation from two sources: weather stations and hydro gauges, which are located at some distance from each other. The problem can be illustrated by
Figure 4. Thereby, some parameters require interpolation to neighboring points for forming the complete dataset for each gauging station.
Even a simple interpolation algorithm can be used to resolve this problem. But there is a need to keep the approach flexible: some weather stations that are close (by longitude and latitude coordinates) to the gauging station can represent the real situation in a non-precise way. It can be caused by topography inhomogeneities.
For example, the points are close to each other, but the nearest weather or gauging station is located in the lowlands, and the two neighboring ones are located in the hollows among the ridges. In this case, the best solution would be to take values only from the nearest weather station and not to interpolate at all. In the other case, a good solution would be to average the values from five neighboring weather stations.
Bilinear interpolation and nearest-neighbor interpolation are not suitable for such tasks. Therefore, it was decided to implement an approach where the K-nn (K-nearest neighbor) machine learning model would interpolate the values. The prediction of the new value of the meteorological parameter is based on two predictors in this case: latitude and longitude. The number of neighboring weather stations for the required gauging stations can be changed. The categorical indicators can also be “interpolated” with this approach. In this case, it is necessary to replace the K-nn regression model with the classification model.
The other problem that can be found during data preprocessing is the presence of gaps. Various ways of gap-filling can be applied to time series of meteorological, hydrological, or other types of environmental data. Such gap-filling methods include relatively simple ones, based on linear or spline interpolation. In more advanced approaches linear regression such as ARIMA [
56], ensemble methods, gradient boosting [
57] or even neural networks approach [
58,
59] can be used.
Also, more complicated gap-filling approaches exist. the paper [
60] shows that one of the most accurate ways is a bi-directional time series forecast adapted for gap-filling. So, it was decided to fill the gaps based on the available preceding and succeeding parts of the time series. Also, there are ‘native’ gaps in the indicators related to ice conditions and snow cover—for the warm season it was not filled for obvious reasons.
For this research, two methods of gap-filling were used depending on the size of the gap. There were two general types of data: with pronounced seasonal component and possessing some stationarity. While the size of the gap is small and calculations are in values of up to ten or the time series especialty is stationarity, the autoregressive algorithm was used. It provides less evaluation time and sufficient quality in such cases. But for lengthy gaps and for time series with seasonality this approach as any other linear approaches lead to inadequate results due to its specificity. This case is quite common in the analyzed data of river monitoring-for some time series gaps reached several years.
For solving this problem, the following method was used. First of all, time series with gaps was decomposed into three components: trend, seasonality, and residuals. Decomposition was provided by the LOESS (locally estimated scatterplot smoothing) method, which is common to use with natural data [
61,
62].
The several years of recordings were lost in data, but all time-series include thirty years of observations, seasonal and trend components, which is the most significant to keep. The combination of trend, seasonality and median value of the data in the range of the gap fills it preserving the general peculiarities of time series. The results of the approach described above are presented in
Figure 5.
2.4. Time Series Forecasting
Currently, an approach based on the analysis of signals produced by the system is widely used to study the properties of complex systems, including in experimental studies. This is very relevant in cases where it is almost impossible to mathematically describe the process under study, but we have some characteristic observable values at our disposal. Therefore, the analysis of systems, especially in experimental studies, is often implemented by processing the recorded signals—time series. For example, in meteorology—time series from meteorological observations, etc.
It should be noted that the time series differs significantly from tabular data since its analysis takes into account not only the statistical characteristics of the sample [
63], but also the temporal relationship. There are two main directions for the time series analysis: statistical (probabilistic models, autoregressive models) and machine learning approaches.
Autoregressive models with a moving average (ARIMA) are used for statistical processing of the time series. When using such models, it is necessary to bring the initial series to a stationary form, which can be done using operations of trend removal application of statistical estimates and noise filtering.
The set of models and methods that should be developed to apply ML to real data should be selected according to the properties of the data and the modeling task. Automated machine learning (AutoML) technologies can be used to simplify the design process of such models. The automatic creation of ensemble models can improve the quality of modeling of multiscale processes. The specifics of these data require a specific approach to their processing.
This section discusses the application of composite pipelines obtained using automatic machine learning algorithms to better predict multiscale processes represented by sensor data. The proposed approach is based on the decomposition of the data stream and correction of the modeling error achieved due to the specific structure of the composite pipeline. However, simply adding or mixing multiple models may not be enough to handle real data sets.
We can analyze a model created using the AutoML is details as shown in
Figure 6. It can be divided into two sub-pipelines: “smoothing-ridge-ridge regression” and “ridge-ridge regression”, which are combined using the “ridge regression” node. The nodes of the algorithm contain various operations. Using the described approach, the pipeline can be configured in the following way: one of the models analyzes the periodic component, and the other analyzes the components associated with trends.
The smoothing operation is a Gaussian filter. Mathematically, the Gaussian filter modifies the input signal by convolution with the Gaussian function; this transformation is also known as the Weierstrass transform. It is considered an ideal filter in the time domain.
The lagged operation is a comparison of a time series with a sequence of multidimensional lagged vectors. An integer L (window length) is selected such that. These vectors form the trajectory matrix of the original time series. This type of matrix is known as the Hankel matrix elements of the anti-diagonals (that is, the diagonals going from bottom to left to right) are equal.
Ridge regression is a variation of linear regression, specially adapted for data that demonstrate strong multicollinearity (that is, a strong correlation of features with each other). The consequence of this is the instability of estimates of regression coefficients. Estimates, for example, may have incorrect signs or values that far exceed those that are acceptable for physical or practical reasons.
The pipeline “lagged-ridge regression” transforms the maximum daily water level one-dimensional time-series into a trajectory matrix using a one-parameter shift procedure. This makes it possible to use lagged vectors as features for a machine learning model without involving exogenous data. Furthermore, ridge regression is applied to the obtained trajectory matrix, since it is more likely that some columns of the matrix are correlated with each other. It can lead to unstable estimates of regression coefficients. Adding a filtering operation allows “smoothing out” the original time series, reducing the variance and increasing the conditionality of the trajectory matrix at the stage of lagged transformation. Visualization of the composite pipeline and operations in the nodes of this model is shown in the
Figure 7.
The approaches described above were implemented in the AutoML framework FEDOT. This allowed us to quickly identify models when forecasting time series. Based on this, we can say that the composite pipeline obtained using AutoML contains an interpretation of physical processes described by a time series, since lagged vectors are used as features that reflect the cyclicity and variability of processes. And at the same time, this model takes into account the features of the data from the point of view of machine learning.
2.5. Multi-Output Regression
Also, we implemented a multi-regression model as an additional block of the composite pipeline. We used the data historical data from weather stations and level gauges (
Table 2) to find the dependence between the target variables and the features.
Figure 8 presents the dynamics of the daily water level and the snow height simultaneously. The peaks of the orange curve can be interpreted as periods of snow accumulation and extremes below zero can be called periods of snow melting. When the snow reaches a minimum, the water level begins to rise.
The target variable is a water level that depends on the features. In our case, it is important to use not only the values at a current time of these features but also to take into account the values over a period of time.
As an example, the correlation between the target variable and snow height can be analyzed. To take into account whether the amount of snow decreased or increased over the past few days, data aggregation can be used. We use several aggregation functions: average, amplitude, most frequent, and summation value. The features in
Table 3 are calculated as an aggregation state for the past seven days, and the columns (“1”, “2” etc.) are water level predictions for the seven days ahead.
It can be useful to take a closer look at the example with the amplitude of snow cover height. We want to calculate the amount of melted snow over the past few days, as it strongly correlates with the water level. In the case of snow height, this is not exactly the amplitude, where the value is calculated by the formula max–min. For snow height, we count the amount of melted precipitation over a certain time. The considered example covers the period from 10 April 2020, to 30 April 2020, and the time interval for aggregation is equal to seven days. In this case, we can find the difference between the current and past day observations and accumulate difference if it is less than zero and continue accumulating for the aggregating interval. So we can know “how many cm of snow melted during the seven days”.
Figure 9 can be used to explain the process of features aggregation. The red line shows the actual values of the snow height and the green line shows the aggregation state of the accumulated melted snow over the past seven days. Let’s pay attention to the time period indicated by the orange line, when the actual amount of snow decreases, the amount of melted snow increases, which well describes the water level. In this case, accumulated value allows estimating the amount of snow that has melted over a period of time and using it as a feature for prediction.
We have made similar transformations for other meteorological parameters. However, there is a categorical feature describing the events on the river, and they are recorded in the form of phrases including “Ice drifts”, “Excitement”, “Incomplete freeze-up”, “Jam above the station”, etc. We decided to rank the events (
Table 4) according to the degree of influence on the water level in the river and have already applied aggregation-sum to the ranked estimates. If the sum of the ranks is large, then we should expect a noticeable change in the water level in the river and vice versa.
The set of additional features were obtained during the process of data preprocessing and aggregation. Regular features are:
temp (FLOAT)—average daily water temperature.
ice-thickness (INT)—thickness of ice.
snow-height (INT)—the height of snow on ice.
discharge (FLOAT)—average daily water consumption, m/s.
water-level (INT)—is the target variable indicating the maximum water level.
Aggregated features are:
events—(TEXT)—the sum of events ranked by the degree for 30 days, correlated to the water level.
discharge-mean (FLOAT)—average for five days water consumption, m/s.
temp-min (FLOAT)—minimum temperature on water level for 7 days. At low temperatures, ice formation, slowing of the river flow and, as a result, an increase in the water level is possible.
ice-thickness-amplitude (INT)—amplitude thickness of ice for seven days shows an increase or decrease in the thickness of the ice.
snow-height-amplitude (INT)—amplitude of snow height. Directly proportional to the water level.
water-level-amplitude (INT)—the prediction of the water level depends heavily on the data for the past few days. By aggregating the values for the past seven days, we are essentially trying to predict a time series.
The prepared set of features allow us to build a multi-target regression model to predict the water level for several days ahead. We decided to use the AutoML-based approach to generate the multi-target regression pipelines that consist of models and data operations. The best-found pipelines, based on validation data for flood forecasting, are presented in
Figure 10.
The presented pipeline consists of two types of nodes: primary (blue) and secondary (green); raw data is received in primary nodes. Each node is a model or an operation on data. In the upper left corner, there is a pipeline, where the primary node is the principal component analysis block. It is an operation on data that reduces the feature space while not losing useful information for prediction. The secondary node in the pipeline is a random forest regression, which is a model to give a final prediction. The combining models and operations make it possible to build the sub-optimal pipeline that is effective in terms of the predictive accuracy for the water level for seven days ahead. The identification and optimization of the structure were conducted using the composite AutoML approach described above.
2.6. Physical Modelling
In addition to the presented data-driven approaches, we chose to include a physics-based element into the ensemble. As the base for our model we have utilized SRM (Snowmelt-Runoff Model) [
33], which is designed to calculate water discharge for the mountainous river basins, where water, incoming into the river, originates from melting snow and rain. The following assumption is stated: all discharge is generated by sources inside the processed basin. It is limiting the model scope to the minor rivers. However, in the analyzed case, the Lena river has a large water catchment area, that has varying conditions and additional gauges located upstream which can be used for discharge evaluations. We tried to alleviate the scope restriction by introducing a transfer term, that connects the discharge in the downstream gauge with the discharge of the upstream one in the previous day.
The main input variables, used in the SRM model, include temperature, from which the number of degree-days
is calculated, snow cover
, and rainfall
. To initialize the modeling, a number of basin parameters shall be determined: snowmelt and rain runoff coefficients (
and
correspondingly, dimensionless parameters), degree-day factor (
C
), and area
A (
). Additionally, we have to compute the recession coefficient
, and
defining the transfer of the river water between gauges (dimensionless), where
k and
have to be evaluated during the periods with no additional water intake into the river. The final equation for the discharge calculation took form (
1), where we make the prediction for the
m-th gauge at
n-th time point.
To calibrate the model we have utilized the differential evolution algorithm, that searched for the model parameters, that produce the minimal error between model predictions and observed values on the historical observations. The optimized function took form of discrepancy between prediction
, calculated by the Equation (
1), and observed value
, that has to be optimized in response to the parameter vector
. The specifics of the problem have introduced a number of constraints, caused by reasonable boundaries of parameters.
The calibration was performed in two stages. At first, the data from the processed period was split into two datasets by the presence of water input from the catchment. The following assumption was stated: in periods with no snow cover and no rainfall, the river discharge is determined only by the recession coefficient and the transfer. The stage of the calibration was performed on this partial data for the reduced Equation (
3). On the data, that describes periods of water intake from the part of catchment, corresponding to the studied gauge, the search of the remaining parameters was initialized.
Due to the simplicity of the proposed model, it can be relatively easy to interpret the forecasts. By evaluating the terms of the Equation (
1), model’s users can analyze which factor between rainfall or snow melt contributes to the alteration of river discharge in the particular moment. The variation of the river discharge, caused by these factors, can be fully interpreted.
The final stage of the SRM-based approach is the transition from river discharge to the water levels. To discover the dependency between these variables, the decision tree model has been trained with the date and the discharge as the independent variables and the maximum daily water level as the dependent one. Generally, the dependency is one-to-one correspondence with the exception of cases, when the river flow is blocked by ice jams.
The input variables, used in the simulation are taken from the field observations and from satellite data. Temperature and precipitation are measured at the meteorological stations and then interpolated to the hydrological gauge in the manner, described in the
Section 2.3.
To assess the amount of snow cover, it was decided not to be limited only to measurement data due to imperfect equipment, as well as the low quality of the results of values interpolation from a point to an area. Therefore for calculating snow cover fraction, remote sensing data from MODIS MOD10A1 product [
64] was used. It provides spatial data, which is more qualitative and complete than information from the meteorological station (
Figure 11).
Accumulation of runoff in each section of the watercourse due to melting of snow cover occurs from a certain territory due to the relief. Extracting watershed by expert manual solution is a laborious process, therefore the segmentation of territory on catchments for each watercourse tributary was implemented with a capacity of GRASS geographic information system (GIS). The algorithm r.watershed works on digital elevation model (DEM) as input data, during processing, calculates water streams and returns the labels for each catchment. Its core is an A
T least-cost search algorithm [
65] designed to minimize the impact of DEM data errors. In this work open-source DEM - Shuttle Radar Topography Mission (SRTM) [
66] was used. Steps of calculating the watersheds for two hydro gauges are presented in
Figure 12.
The Normalized-Difference Snow Index (NDSI), that was obtained from the MODIS remote sensing and used for evaluation of the snow covered areas in the catchment, has reliability issues, when applied to the evergreen coniferous forests, that are common in the Eastern Siberia [
67]. Additionally, the remote sensing data had to be filtered from the measurements, taken in the conditions, when the view from the satellite is obstructed: over the clouds, in nights, etc.
2.7. Quality Metrics for Forecasts
The following metrics were used:
NSE—Nash–Sutcliffe model efficiency coefficient. The metric changes from to 1. The closer the metric is to one, the better;
MAE—Mean Absolute Error. The metric changes from 0 to ∞. The closer the metric is to zero, the better. The units of this metric are the same as the target variable—centimeters;
SMAPE—Symmetric Mean Absolute Percentage Error. Varies from 0 to ∞. The closer the metric is to zero, the better. Measured as a percentage.
The equations for NSE (Equation (
4)), MAE (Equation (
5)) and SMAPE (Equation (
6)) are provided below. The following notation is used:
n = number of elements in the sample,
is the prediction,
the true value and
is averaged observed water level.
The specific approach was used to validate the algorithm using the metrics described above. The composite pipeline is able to provide forecast for n days ahead with the following time steps for forecast . In this case, the retrospective data X is used to train the models in the pipeline. To prepare a forecast for the interval from to the m values of the predictor for time steps are required. Respectively, the sub-sample of retrospective data is required to obtain the forecast from to . The trained pipeline can predict the values for n next elements if the set of predictors with the specified length is provided. So, the length of the validation part of the time series can be arbitrary. In the paper, the length of the validation horizon was equal to 805 elements (days).
The distribution of error across forecast horizons was also additionally investigated. For this purpose Metrics were measured only on forecasts of 1, 2, 3, 4, 5 and 7 days in advance. In addition to calculating metrics, an extensive analysis of graphical materials: predictions and error plots are presented.
4. Discussion
The proposed approach for the automated design of composite forecasting pipelines was validated on ten hydro gauges and two years of observations. In total, more than 8000 points were involved in the validation and comparison experiments.
Figure 13 and
Figure 14 demonstrate that even individual models can produce forecasts with small errors (SMAPE less than 32%) and relatively good efficiency metric NSE—bigger than 0.72. The use of ensembling made it possible to obtain an even better value: NSE 0.80. At the same time, comparison between predictions of the individual models and ensemble highlights that the composite pipeline produces a higher forecast error on the validation set by MAE and SMAPE. Note that the values of the metrics differ insignificantly. This may be because the ensemble has become more robust to distortions in the data, but is worse at reproducing absolute values in peaks during high water. So, NSE increased for ensemble, but error metrics such as MAE and MAPE became a little worse or stayed almost the same.
Metrics were also calculated for the most important period: from April to July. At this time, the highest water levels are typically observed on each hydro gauge. And the results showed that the ensemble metrics at these time sites sections are noticeably better (
Table 5): NSE for time series model—0.60, for multi-target model—0.61, and for ensemble—0.71. So, the ensemble model allows achieving a significant increase of forecast precision exactly during the most difficult periods for forecasting.
The robustness of the algorithm to the presence of gaps in the initial data has been investigated (
Table 7). According to the results of the experiments, it is shown that an increase in the gaps in the original data (up to 40%), leads to a slight decrease in NSE—12%. At the same time, other error metrics increased compared to training the algorithm on data without gaps: MAE increased by 42% and SMAPE by 54%. It is worth noting that the gap ratio of 40% is quite a large number. So, it is worth using ML and AutoML algorithms on data where the proportion of omissions is much smaller (up to 20%).
Additionally, the dependence of ensemble and individual blocks error on different parts of the data was investigated: on the training sample, the test sample, and the validation sample (
Table 6). It is shown that the use of an ensemble of models avoids a significant increase in the forecast error on new data. So, the NSE for the composite pipelines decreased from 0.94 on the training sample to 0.84 on the validation sample (0.10 units). At the same time, the average decrease in NSE for individual blocks was 0.15.
A comparison with competing algorithms showed that the proposed approach is more efficient than the expert-configured AR (NSE 0.67) and ARIMA (NSE 0.69) models. Moreover, the physical SRM (NSE 0.74) is also inferior in all considered metrics to the composite approach.
In the tasks related to the modeling of hazardous events, the ability to interpret the forecast and understand how it was obtained from the model by an expert is highly desired. While the majority of the introduced ensemble elements lack the interpretability of their modeling results, the forecasts of the physics-based block (e.g., SRM), can be explained. Therefore, by obtaining the separate forecasts of the introduced models and the combined ensemble output, the expert will be able to analyze the nature of the river level changes by comparing tendencies with the SRM block.
Disadvantages of the proposed approach include the difficulty of combining forecasts between blocks. Other limitations in the applicability of the modeling approach can be traced back to the general limitations of data-driven methods. The insufficient or inaccurate measurements, prevalent in sparsely-populated regions, can result in the necessity to use limited training data or apply gap-filling or filtering algorithms. Any alterations in the river flow, e.g., damming of the river or melting of the glaciers in the catchment, can disturb the observed hydrological patterns and make the development of data-driven models impossible.
The snowmelt-runoff model can be introduced into the ensemble to model the gauges, that have both discharge and water level measurements. Such gauges are relatively uncommon in the available data due to the difficulties of measuring the discharge of the large rivers.
On the other hand, the advantages are low forecasting error, native interpretability due to the presence of a physical model in its structure, and robustness to distortions in data and lack of information. Moreover, individual blocks in the composite pipeline are proposed to be identified using an evolutionary algorithm. This allows automating the system deployment process. Another important feature of the composite approach is modularity. It is possible to use only subset of suitable models and to combine them into an ensemble if necessary.
The proposed approach can be improved. To increase the quality of the ensemble results, two opposite approaches can be used. The first approach is aimed at the enhancement of the individual forecasts of the ensemble blocks. Deep learning techniques, e.g., LSTM networks, can be used to improve the quality of the time-series forecasts. Moreover, different architectures of neural networks and different ML models can replace the multi-output regression. Furthermore, more sophisticated physics-based models that take into consideration the water dynamics can be added. Other data sources can be involved as the features for the data-driven elements.
The second approach is based on the development of better forecast integration techniques to form ensemble predictions. For example, the meta-algorithm, that is currently used, may be replaced by the softmax techniques, heuristic methods of combining the answers of basic algorithms (using visualizations, learning in special subspaces, etc.). Other special encodings of target values and reduction of the problem solution to the solution of several tasks also can improve ensemble. One of the most popular techniques here is ECOC (encoding output with error correction), the other is tuning for different transformations of the target feature.
5. Conclusions
In the paper, the automated approach for short-term river flood forecasting is proposed. It allows (1) identifying the composite pipelines that include machine learning methods and domain-specific models; and (2) using it for the prediction of future floods or the reconstruction of historical events. The implemented combination of data-driven and physical models in a single pipeline makes it possible to enrich the models by existing knowledge (as it is proposed in concepts of composite AI).
The validation of this approach is conducted using the Lena River case study. As a result of the application of the proposed approach, a composite pipeline for flood forecasting was identified. The presented model consists of three blocks, two of which are based on machine learning methods and one on the physical Snowmelt-Runoff-Model. The described approach relies on AutoML algorithms to identify the structure of machine learning models. So, this allows fast construction of composite pipelines on different data sources and at the same time identifies robust models. A Random Forest model was used to ensemble the predictions, which hyperparameters were tuned using a Bayesian approach.
The obtained pipeline was validated on ten hydro gauges and two years of daily observations of maximum water levels. The composite pipeline showed the best metrics on the validation set: NSE 0.80. At the same time, individual blocks of such ensemble got the following metrics: 0.74 for time series and 0.72 for the multi-target regression model. Validation was also performed for the high water period (April–July) to ensure that the model predicts spring floods well enough. It was shown that the quality of the forecast is slightly lower in this case, but still remains at a fairly high level—0.71. Comparative analysis with algorithms-competitors proves that the proposed ensemble is more effective than expert-configured AR (NSE 0.67), ARIMA (NSE 0.69), or stand-alone SRM (NSE 0.84).
Also, we can conclude that the large size of the retrospective data makes it is possible to build a sufficiently effective time series forecasting model based on only autoregressive dependencies. The high value of NSE—0.74 and low values for other metrics (MAE—45.02 and SMAPE—28.44) confirm this hypothesis. However, results for the ensemble of models prove its ability to significantly reduce forecast error.
In this study, we applied an approach to predict water levels for both the high water period during spring and the entire year. Although it was validated on the Lena River, this approach can be generalized for other rivers as well. For example, Canadian rivers such as the Mackenzie, Peace-Athabasca and Slave River have common regimes with significant floodings due to ice jams [
69]. It was achieved by automating the process of building composite data-driven models with the help of AutoML techniques (implemented as a part of the open-source FEDOT framework available in
https://github.com/nccr-itmo/FEDOT (accessed on 6 December 2021)).